Aufgaben:Exercise 1.5: Reconstruction of the Jakes Spectrum: Unterschied zwischen den Versionen
Javier (Diskussion | Beiträge) K (Javier verschob die Seite Exercises:Exercise 1.5: Reconstruction of the Jakes Spectrum nach Exercise 1.5: Reconstruction of the Jakes Spectrum) |
|||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Statistische Bindungen innerhalb des Rayleigh-Prozesses}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Statistische Bindungen innerhalb des Rayleigh-Prozesses}} | ||
| − | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame| | + | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame|Considered Jakes spectrum]] |
| − | + | In a mobile radio system, the [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Doppler effect]] is also noticeable in the power density spectrum of the Doppler frequency $f_{\rm D}$ . | |
| − | + | This results in the so-called [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading|Jakes spectrum]], which is shown in the graph for the maximum Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$. ${\it \Phi}_z(f_{\rm D})$ has only portions within the range $± f_{\rm D, \ max}$, where | |
| − | + | $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2} } | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | What is expressed in the frequency domain by the power spectral density (PSD) is described in the time domain by the autocorrelation function (ACF). The ACF is the ${\it \Phi}_z(f_{\rm D})$ by the [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation#Das_zweite_Fourierintegral|inverse Fourier transform]] of the PSD. | |
| − | + | With the <i>Bessel function</i> of the first kind and zero order $({\rm J}_0)$ you get | |
| − | + | $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | |
| − | + | To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading|Rayleigh channel model]], each with the frequency response $H_{\rm DF}(f_{\rm D})$. | |
| − | + | The dimensioning of these filters is part of this task. | |
| − | * | + | *We restrict ourselves here to the branch for generating the real part $x(t)$. The ratios derived here are also valid for the imaginary part $y(t)$. |
| − | * | + | *At the input of the left digital filter of the [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading|Rayleigh channel model]] , there is white Gaussian noise $n(t)$ with variance $\sigma^2 = 0.5$. |
| − | * | + | *The real component is then obtained from the following convolution |
:$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | :$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | ||
| − | + | ''Notes:'' | |
| − | + | * This task belongs to the subject area [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses|Statistische Bindungen innerhalb des Rayleigh–Prozesses]]. | |
| − | + | * The digital filter is treated in detail in chapter [[Stochastische_Signaltheorie/Digitale_Filter|Digitale Filter]] of the book „Stochastic Signal Theory”. | |
| − | '' | ||
| − | * | ||
| − | * | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the value of the Jakes, spectrum of the real part at the Doppler frequency $f_{\rm D} = 0$? |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_x(f_{\rm D} = 0)\ = \ $ { 1.59 } $\ \cdot | + | ${\it \Phi}_x(f_{\rm D} = 0)\ = \ $ { 1.59 } $\ \cdot 10^{\rm –3} \ 1/{\rm Hz}$ |
| − | { | + | {Which dimensioning is correct, where $K$ is an appropriately chosen constant? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It holds $H_{\rm DF}(f_{\rm D}) = K \cdot {\it \Phi}_x(f_{\rm D})$. |
| − | + | + | + It applies $|H_{\rm DF}(f_{\rm D})|^2 = K \cdot {\it \Phi}_x(f_{\rm D})$ |
| − | { | + | {From which condition can the constant $K$ be determined? |
|type="[]"} | |type="[]"} | ||
| − | - $K$ | + | - $K$ can be selected as desired. |
| − | - | + | - The integral over $|H_{\rm DF}(f_{\rm D})|$ must equal $1$ . |
| − | + | + | + The integral over $|H_{\rm DF}(f_{\rm D})|^2$ must be $1$ . |
| − | { | + | {Is $H_{\rm DF}(f)$ unambiguously defined by the two conditions according to '''(2)'' and '''(3)'''? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes. |
| − | + | + | + No. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The Jakes spectrum of the real part is half the resulting spectrum ${\it \Phi}_z(f)$: |
:$${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = | :$${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = | ||
\frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} | \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} | ||
| Zeile 66: | Zeile 63: | ||
| − | '''(2)''' | + | '''(2)''' <u>Solution 2</u> is correct: |
| − | * | + | *The input signal $n(t)$ has a white (constant) LDS ${\it \Phi}_n(f_{\rm D})$. |
| − | * | + | *The PSD at the output is then |
| − | + | $${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' <u>Solution 3</u> is correct. |
| − | * | + | *Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$. |
| − | |||
| − | '''(4)''' <u> | + | '''(4)''' <u>No</u>: |
| − | * | + | *The two conditions after subtasks (2) and (3) only refer to the magnitude of the digital filter. |
| − | * | + | *There is no constraint for the phase of the digital filter. |
| − | * | + | *This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results. |
| − | *In | + | *In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration. |
| − | + | The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see: | |
| − | [[ | + | [[File:EN_Mob_A_1_5d.png|right|frame|Approximation of the Jakes spectrum and ACF]] |
| − | * | + | * The Jakes power spectral density (left graph) can only be reproduced very inaccurately due to the vertical drop at $± f_{\rm D, \ max}$. |
| − | * | + | * For the time domain, this means that the ACF decreases much faster than theory suggests. |
| − | * | + | *For small values of $\delta t$, however, the approximation is very good (right graph). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 11. Mai 2020, 15:15 Uhr
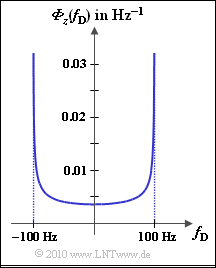
In a mobile radio system, the Doppler effect is also noticeable in the power density spectrum of the Doppler frequency $f_{\rm D}$ .
This results in the so-called Jakes spectrum, which is shown in the graph for the maximum Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$. ${\it \Phi}_z(f_{\rm D})$ has only portions within the range $± f_{\rm D, \ max}$, where $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2} } \hspace{0.05cm}.$$
What is expressed in the frequency domain by the power spectral density (PSD) is described in the time domain by the autocorrelation function (ACF). The ACF is the ${\it \Phi}_z(f_{\rm D})$ by the inverse Fourier transform of the PSD.
With the Bessel function of the first kind and zero order $({\rm J}_0)$ you get $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$
To take into account the Doppler effect and thus a relative movement between transmitter and receiver in a system simulation, two digital filters are inserted in the Rayleigh channel model, each with the frequency response $H_{\rm DF}(f_{\rm D})$.
The dimensioning of these filters is part of this task.
- We restrict ourselves here to the branch for generating the real part $x(t)$. The ratios derived here are also valid for the imaginary part $y(t)$.
- At the input of the left digital filter of the Rayleigh channel model , there is white Gaussian noise $n(t)$ with variance $\sigma^2 = 0.5$.
- The real component is then obtained from the following convolution
- $$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$
Notes:
- This task belongs to the subject area Statistische Bindungen innerhalb des Rayleigh–Prozesses.
- The digital filter is treated in detail in chapter Digitale Filter of the book „Stochastic Signal Theory”.
Questionnaire
Sample solution
- $${\it \Phi}_x(f_{\rm D} = 0) = {\it \Phi}_y(f_{\rm D} = 0) = \frac{{\it \Phi}_z(f_{\rm D} = 0)}{2}= \frac{\sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max}} = \frac{0.5}{\pi \cdot 100\,\,{\rm Hz}} \hspace{0.15cm} \underline{ = 1.59 \cdot 10^{-3}\,\,{\rm Hz^{-1}}} \hspace{0.05cm}.$$
(2) Solution 2 is correct:
- The input signal $n(t)$ has a white (constant) LDS ${\it \Phi}_n(f_{\rm D})$.
- The PSD at the output is then
$${\it \Phi}_x(f_{\rm D}) = {\it \Phi}_n(f_{\rm D}) \cdot | H_{\rm DF}(f_{\rm D}|^2 \hspace{0.05cm}.$$
(3) Solution 3 is correct.
- Only if this condition is fulfilled, the signal $x(t)$ has the same variance $\sigma^2$ as the noise signal $n(t)$.
(4) No:
- The two conditions after subtasks (2) and (3) only refer to the magnitude of the digital filter.
- There is no constraint for the phase of the digital filter.
- This phase can be chosen arbitrarily. Usually it is chosen in such a way that a minimum phase network results.
- In this case, the impulse response $h_{\rm DF}(t)$ then has the lowest possible duration.
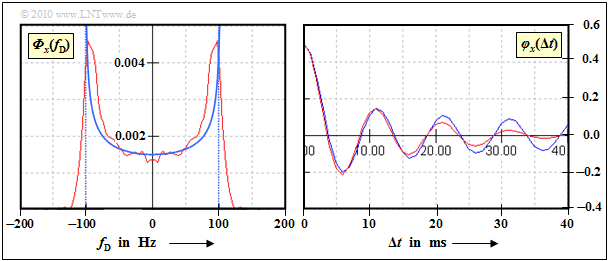
The graph shows the result of the approximation. The red curves were determined simulatively over $100\hspace{0.05cm}000$ samples. You can see:
- The Jakes power spectral density (left graph) can only be reproduced very inaccurately due to the vertical drop at $± f_{\rm D, \ max}$.
- For the time domain, this means that the ACF decreases much faster than theory suggests.
- For small values of $\delta t$, however, the approximation is very good (right graph).