Aufgabe 5.3: Digitales Filter 1. Ordnung

• Zurück zum Buch

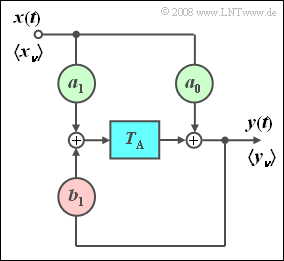
Wir betrachten die nebenstehende Filteranordnung mit den Koeffizienten a₀, a₁ und b₁, die alle Werte zwischen 0 und 1 annehmen können.

Das Eingangssignal ist ein einziger Diracimpuls mit dem Einheitsgewicht „1” – also x(t) = δ(t) – was der folgenden zeitdiskreten Darstellung entspricht:

$$\left\langle {x_\nu } \right\rangle = \left\langle {1,\;0,\;0,\;0,\;...} \right\rangle .$$

Aufgrund dieser speziellen Eingangsfolge beschreibt die Folge 〈y_ν〉 am Filterausgang gleichzeitig die zeitdiskrete Impulsantwort des Filters. Der Abstand der Abtastwerte beträgt hierbei T_A = 1 μs.

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.2.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Der Sonderfall b1 = 1 führt zu einem nichtrekursiven Filter.
	Es gilt y(t) = x(t), wenn a0 = 1, a1 = 0, b1 = 0 gewählt wird.
	Mit a0 = 0, a1 = 0.5, b1 = 0 ist y(t) gegenüber x(t) unverzerrt.

2

Es gelte nun a₀ = 1, a₁ = 0 und b₁ = 0.6. Berechnen Sie die Ausgangsfolge 〈y_ν〉. Welcher Ausgangswert y₃ tritt zum Zeitpunkt t = 3 · T_A auf?

$a_1 = 0:\ \ y_3$ =

3

Auf welchen Bereich 0, ... , M · T_A ist die Impulsantwort beschränkt, wenn man Werte kleiner als 0.001 vernachlässigt? (a₀ = 1, a₁ = 0, b₁ = 0.6)

$M$ =

4

Es gelte weiter a₀ = 1 und b₁ = 0.6. Berechnen Sie unter Berücksichtigung des Ergebnisses aus (b) den Ausgangswert y₃ für a₁ = –0.5.

$a_1 = -0.5:\ \ y_3$ = {0.036 3% }

Musterlösung

Musterlösung

1.  Das Filter ist nichtrekursiv, wenn die Rückführung entfällt: b₁ = 0. Sind zusätzlich a₀ = 1 und a₁ = 0, so sind die Folgen 〈x_ν〉 und 〈y_ν〉 und damit natürlich auch die Signale x(t) und y(t) gleich. Mit a₀ = 0 und a₁ = 1 ist y(t) = x(t – T_A) um T_A verzögert, mit a₁ = 0.5 zusätzlich gedämpft. Verzögerung und Dämpfung haben jedoch keine Verzerrung zur Folge. Richtig sind somit die Lösungsvorschläge 2 und 3.

2.  Zum Zeitpunkt ν = 0 ist y_ν = x_ν = 1. Für alle weiteren Zeitpunkte ν gilt x_ν = 0 und somit auch:

$$y_\nu = b_1 \cdot y_{\nu - 1} = {b_1 }^\nu .$$

Insbesondere ist y₃ = b₁³ = 0.6³= 0.216.

3.  Entsprechend der Aufgabenstellung muss gelten:

$$y_{M + 1} = {b_1} ^{M + 1} < 0.001.$$

Dies führt zum Ergebnis:

$$M + 1 \ge \frac{{\lg \left( {0.001} \right)}}{{\lg \left( {0.6} \right)}} = \frac{ - 3}{ - 0.222} \approx 13.51.\quad \Rightarrow \quad \hspace{0.15cm} \underline{M = 13}.$$

Die Überprüfung der Werte y₁₃ ≈  0.0013 und y₁₄ ≈  0.0008 bestätigt dieses Ergebnis.

4.  Aufgrund der Linearität des vorliegenden Filters erhält man das gleiche Ergebnis, wenn man das Filter gegenüber Punkt b) nicht verändert (a₁ = 0) und dafür die Eingangsfolge

$$\left\langle {x_\nu } \right\rangle = \left\langle {1,\; - 0.5,\;0,\;0,\;...} \right\rangle$$

berücksichtigt. Man erhält dann allgemein für ν > 0:

$$y_\nu = {b_1} ^\nu + a_1 \cdot {b_1} ^{\nu - 1} = \left( {b_1 + a_1 } \right) \cdot {b_1} ^{\nu - 1} .$$

Mit b₁ = 0.6 und a₁ = –0.5 ergibt sich daraus

$$y_\nu = 0.1\cdot {0.6} ^{\nu - 1} ,$$

und somit die Folge:

$$\left\langle {y_\nu } \right\rangle = \left\langle {1,\;0.1,\;0.06,\;0.036,\;...} \right\rangle .$$

Der gesuchte Wert ist y₄ = 0.036.