Aufgabe 4.2: Tiefpass zur Signalrekonstruktion

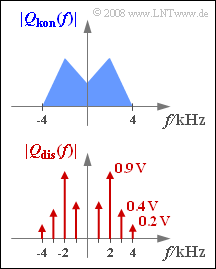
Wir betrachten in dieser Aufgabe zwei verschiedene Quellensignale $q_{kon}(t)$ und $q_{dis}(t)$, deren Spektralfunktionen $|Q_{kon}(f)|$ und $|Q_{dis}(f)|$ grafisch dargestellt sind. Die höchste in den Signalen vorkommende Frequenz ist jeweils $4 kHz$.

Von der Spektralfunktion $Q{kon}(f)$ ist nicht mehr bekannt, als dass es sich um ein kontinuierliches Spektrum handelt, wobei:

$$Q_{\rm kon}(|f| \le 4\,{\rm kHz}) \ne 0 \hspace{0.05cm}.$$

Das Spektrum $Q_{dis}(f)$ beinhaltet Spektrallinien bei $±1 kHz$, $±2 kHz$, $±3 kHz$ und $±4 kHz$. Somit gilt:

$$q_{\rm dis}(t) = \sum_{i=1}^{4}C_i \cdot \cos (2 \pi \cdot f_i \cdot t - \varphi_i)$$ mit $C_1 = 1.0 V$, $C_2 = 1.8 V$, $C_3 = 0.8 V$, $C_4 = 0.4 V$. Die Phasenwerte $φ_1$,$φ_2$ und $φ_3$ liegen jeweils im Bereich $±180°$ und es gilt $φ_4 = 90°$.

Die Signale werden jeweils mit der Frequenz $f_A$ abgetastet und sofort einem idealen, rechteckförmigen Tiefpass mit der Grenzfrequenz $f_G$ zugeführt. Dieses Szenario gilt zum Beispiel für

die störungsfreie Pulsamplitudenmodulation (PAM) und
die störungsfreie Pulscodemodulation (PCM) bei unendlich großer Quantisierungsstufenzahl M.

Das Ausgangssignal des (rechteckförmigen) Tiefpasses wird als Sinkensignal $υ(t)$ bezeichnet, und für das Fehlersignal gilt $ε(t) = υ(t) – q(t)$. Dieses ist nur dann von 0 verschieden, wenn die Parameter der Abtastung ($f_A$) und/oder der Signalrekonstruktion ($f_G$) nicht bestmöglich dimensioniert sind.

Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 4.1.

Fragebogen

Musterlösung

1. Richtig ist nur die erste Aussage. Die Abtastung von $q_{dis}(t)$ mit der Abtastfrequenz $f-A = 8 kHz$ führt zu einem irreversiblen Fehler, da $Q_{dis}(f)$ einen diskreten Spektralanteil (Diraclinie) bei $f_4 = 4 kHz$ beinhaltet und der Phasenwert $φ_4 ≠ 0$ ist. Mit dem hier angegebenen Phasenwert $φ_4 = 90°$ (4 kHz– Sinuskomponente) gilt $ε_{dis}(t) = υ_{dis}(t) – q_{dis}(t) = –0.4 V · sin(2π · f_4 · t)$. Siehe auch Musterlösung zur Aufgabe Z4.2.

Dagegen kann das Signal $q_{kon}(t)$ mit dem kontinuierlichen Spektrum $Q_{kon}(f)$ auch dann mit einem Rechteck–Tiefpass (mit der Grenzfrequenz $f_G = 4 kHz$) vollständig rekonstruiert werden, wenn die Abtastfrequenz $f_A = 8 kHz$ verwendet wurde. Für alle Frequenzen ungleich $f_4$ ist das Abtasttheorem erfüllt. Der Anteil der $f_4$–Komponente am gesamten Spektrum $Q_{kon}(f)$ ist aber nur verschwindend klein ⇒ $Pr(f_4) → 0$, solange das Spektrum bei f4 keine Diraclinie aufweist.

2. Mit $f-A = 10 kHz$ wird das Abtasttheorem in beiden Fällen erfüllt und mit $f_G = f_A/2$ sind beide Fehlersignale $ε_{kon}(t)$ und $ε_{dis}(t)$ gleich 0 ⇒ Richtig ist nur der Lösungsvorschlag 1.

Die Signalrekonstruktion funktioniert darüber hinaus auch dann, solange $f_G > 4 kHz$ und $f_G < 6 kHz$ gilt.

3. Mit $f_G = 3.5 kHz$ entfernt der Tiefpass fälschlicherweise den $4 kHz$–Anteil, das heißt dann gilt: $$ v_{\rm dis}(t) = q_{\rm dis}(t) - 0.4\,{\rm V} \cdot \sin (2 \pi \cdot f_{\rm 4} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varepsilon_{\rm dis}(t) = - 0.4\,{\rm V} \cdot \sin (2 \pi \cdot f_{\rm 4} \cdot t)\hspace{0.05cm}.$$ ⇒ Richtig ist hier der Lösungsvorschlag 2.

4. Durch die Abtastung mit $f_A = 10 kHz$ ergibt sich das folgende periodische Spektrum:

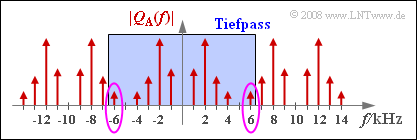
Der Tiefpass entfernt alle diskreten Frequenzanteile mit $|f| ≥ 7 kHz$, nicht aber den $6 kHz$–Anteil. Das Fehlersignal $ε_{dis}(t) = υ_{dis}(t) – q_{dis}(t)$ ist dann eine harmonische Schwingung mit

der Frequenz $f_6 = f_A – f_4 = 6 kHz$,
der Amplitude $A_4$ des $f_4$–Anteils,
der Phase $φ_{–4} = –φ_4$ des $Q(f)$–Anteils bei $f = –f_4$.

⇒ Richtig ist hier der Lösungsvorschlag 3.

	Das Signal $q_{kon}(t)$ lässt sich vollständig rekonstruieren: $ε_{kon}(t) = 0$
	Das Signal $q_{dis}(t)$ lässt sich vollständig rekonstruieren: $ε_{dis}(t) = 0$.

	Das Signal $q_{dis}(t)$ lässt sich vollständig rekonstruieren: $ε_{dis}(t) = 0$.
	$ε_{dis}(t)$ ist eine harmonische Schwingung mit $4 kHz$.
	$ε_{dis}(t)$ ist eine harmonische Schwingung mit $6 kHz$.