Aufgaben:Aufgabe 4.1Z: Andere Basisfunktionen: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Digitalsignalübertragung/Signale, Basisfunktionen und Vektorräume}} | {{quiz-Header|Buchseite=Digitalsignalübertragung/Signale, Basisfunktionen und Vektorräume}} | ||
| − | [[Datei:P_ID1996__Dig_Z_4_1.png|right|frame| | + | [[Datei:P_ID1996__Dig_Z_4_1.png|right|frame|Energiebegrenzte Signale]] |
| − | Diese Aufgabe verfolgt das genau gleiche Ziel wie die [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren| Aufgabe 4.1]]: | + | Diese Aufgabe verfolgt das genau gleiche Ziel wie die [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren| "Aufgabe 4.1"]]: |
| − | Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ \text{...} \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen: | + | Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ \text{...} \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen: |
:$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = | ||
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
| Zeile 13: | Zeile 13: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Mit $M$ Sendesignale $s_i(t)$ können bereits weniger Basisfunktionen $\varphi_{\it j}(t)$ ausreichen, nämlich $N$. Allgemein gilt also $N ≤ M$. | + | Mit $M$ Sendesignale $s_i(t)$ können bereits weniger Basisfunktionen $\varphi_{\it j}(t)$ ausreichen, nämlich $N$. Allgemein gilt also $N ≤ M$. |
| − | Es handelt sich hier um die genau gleichen energiebegrenzten Signale $s_i(t)$ wie in der [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren| Aufgabe 4.1]]: | + | Es handelt sich hier um die genau gleichen energiebegrenzten Signale $s_i(t)$ wie in der [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren| "Aufgabe 4.1"]]: |
| − | *Der Unterschied ist die unterschiedliche Reihenfolge der Signale $s_i(t)$. | + | *Der Unterschied ist die unterschiedliche Reihenfolge der Signale $s_i(t)$. |
| − | *Diese sind in dieser Aufgabe so sortiert, dass die Basisfunktionen auch ohne Anwendung des umständlicheren [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume#Das_Verfahren_nach_Gram-Schmidt| Gram–Schmidt–Verfahrens]] gefunden werden können. | + | |
| + | *Diese sind in dieser Aufgabe so sortiert, dass die Basisfunktionen auch ohne Anwendung des umständlicheren [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume#Das_Verfahren_nach_Gram-Schmidt| "Gram–Schmidt–Verfahrens"]] gefunden werden können. | ||
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume| "Signale, Basisfunktionen und Vektorräume"]]. | |
| − | |||
| − | *Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Signale,_Basisfunktionen_und_Vektorr%C3%A4ume| Signale, Basisfunktionen und Vektorräume]]. | ||
| − | * Verwenden Sie für numerische Berechnungen | + | * Verwenden Sie für numerische Berechnungen $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $ |
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {In Aufgabe 4.1 hat das Gram–Schmidt–Verfahren zu $N = 3$ Basisfunktionen geführt. Wieviele Basisfunktionen benötigt man hier? | + | {In der Aufgabe 4.1 hat das Gram–Schmidt–Verfahren zu $N = 3$ Basisfunktionen geführt. Wieviele Basisfunktionen benötigt man hier? |
|type="{}"} | |type="{}"} | ||
$N \ = \ $ { 3 3% } | $N \ = \ $ { 3 3% } | ||
| − | {Geben Sie die 2–Norm aller Signale an: | + | {Geben Sie die "2–Norm" aller Signale an: |
|type="{}"} | |type="{}"} | ||
$||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | $||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| Zeile 46: | Zeile 45: | ||
|type="[]"} | |type="[]"} | ||
+ Die in Aufgabe 4.1 berechneten Basisfunktionen sind auch hier geeignet. | + Die in Aufgabe 4.1 berechneten Basisfunktionen sind auch hier geeignet. | ||
| − | - Es gibt unendlich viele Möglichkeiten für $\{\varphi_1(t), | + | - Es gibt unendlich viele Möglichkeiten für $\{\varphi_1(t),\ \varphi_2(t),\ \varphi_3(t)\}$. |
| − | - Ein möglicher Satz lautet $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)\}$, mit $j = 1, 2, 3$. | + | - Ein möglicher Satz lautet $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)\}$, mit $j = 1,\ 2,\ 3$. |
| − | + Ein möglicher Satz lautet $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, mit $j = 1, 2, 3$. | + | + Ein möglicher Satz lautet $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, mit $j = 1,\ 2,\ 3$. |
| − | {Wie lauten die Koeffizienten des Signals $s_4(t)$ | + | {Wie lauten die Koeffizienten des Signals $s_4(t)$ bezogen auf die Basisfunktionen $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, mit $j = 1,\ 2,\ 3$? |
|type="{}"} | |type="{}"} | ||
$s_{\rm 41} \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | $s_{\rm 41} \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| Zeile 59: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Der einzige Unterschied zur Aufgabe 4.1 ist die unterschiedliche Nummerierung der Signale $s_i(t)$. | + | '''(1)''' Der einzige Unterschied zur Aufgabe 4.1 ist die unterschiedliche Nummerierung der Signale $s_i(t)$. |
| − | *Damit ist offensichtlich, dass auch hier $\underline {N = 3}$ gelten muss. | + | *Damit ist offensichtlich, dass auch hier $\underline {N = 3}$ gelten muss. |
| − | '''(2)''' Die 2–Norm gibt die Wurzel aus der Signalenergie an und ist vergleichbar mit dem Effektivwert bei leistungsbegrenzten Signalen. | + | '''(2)''' Die "2–Norm" gibt die Wurzel aus der Signalenergie an und ist vergleichbar mit dem Effektivwert bei leistungsbegrenzten Signalen. |
| − | *Die ersten drei Signale haben alle die 2–Norm | + | *Die ersten drei Signale haben alle die "2–Norm" |
:$$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | :$$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | ||
| − | *Die Norm des letzten Signals ist um den Faktor $\sqrt{2}$ größer: | + | *Die Norm des letzten Signals ist um den Faktor $\sqrt{2}$ größer: |
:$$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | :$$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' Die <u>erste und die letzte Aussage sind zutreffend</u> im Gegensatz zu den Aussagen 2 und 3: | + | '''(3)''' Die <u>erste und die letzte Aussage sind zutreffend</u> im Gegensatz zu den Aussagen 2 und 3: |
| − | * Es wäre völlig unlogisch, wenn die gefundenen Basisfunktionen bei anderer Sortierung der Signale $s_i(t)$ nicht mehr gelten sollten. | + | * Es wäre völlig unlogisch, wenn die gefundenen Basisfunktionen bei anderer Sortierung der Signale $s_i(t)$ nicht mehr gelten sollten. |
| − | * Das Gram–Schmidt–Verfahren liefert nur einen möglichen Basisfunktionssatz $\{\varphi_{\it j}(t)\}$. Bei anderer Sortierung ergibt sich (möglicherweise) ein anderer. | + | |
| − | *Die Anzahl der Permutationen von $M = 4$ Signalen ist $4! = 24$. Mehr Basisfunktionssätze kann es auf keinen Fall geben ⇒ der Lösungsvorschlag 2 ist falsch. | + | * Das Gram–Schmidt–Verfahren liefert nur einen möglichen Basisfunktionssatz $\{\varphi_{\it j}(t)\}$. Bei anderer Sortierung ergibt sich (möglicherweise) ein anderer. |
| − | * Wahrscheinlich gibt es (wegen $N = 3$) aber nur $3! = 6$ mögliche Basisfunktionssätze. Wie aus der [[Aufgaben:4.1_Gram-Schmidt-Verfahren| Musterlösung]] zur Aufgabe 4.1 ersichtlich ist, werden sich mit der Reihenfolge $s_1(t), s_2(t), s_4(t), s_3(t)$ die gleichen Basisfunktionen ergeben wie mit $s_1(t), s_2(t), s_3(t), s_4(t)$. Dies ist aber nur eine Vermutung der Autoren; wir haben es nicht überprüft. | + | |
| − | * Die Aussage 3 kann allein schon wegen den unterschiedlichen Einheiten von $s_i(t)$ und $\varphi_{\it j}(t)$ nicht stimmen. Die Signale weisen wie $A$ die Einheit $\sqrt{\rm W}$ auf, die Basisfunktionen die Einheit $\sqrt{\rm 1/s}$. | + | *Die Anzahl der Permutationen von $M = 4$ Signalen ist "$4! = 24$". Mehr Basisfunktionssätze kann es auf keinen Fall geben ⇒ der Lösungsvorschlag 2 ist falsch. |
| − | * Richtig ist somit die letzte Lösungsalternative, wobei für $K$ gilt: | + | |
| + | * Wahrscheinlich gibt es (wegen $N = 3$) aber nur "$3! = 6$" mögliche Basisfunktionssätze. | ||
| + | |||
| + | *Wie aus der [[Aufgaben:4.1_Gram-Schmidt-Verfahren| Musterlösung]] zur Aufgabe 4.1 ersichtlich ist, werden sich mit der Reihenfolge $s_1(t),\ s_2(t),\ s_4(t),\ s_3(t)$ die gleichen Basisfunktionen ergeben wie mit $s_1(t),\ s_2(t),\ s_3(t),\ s_4(t)$. Dies ist aber nur eine Vermutung der Autoren; wir haben es nicht überprüft. | ||
| + | |||
| + | * Die Aussage 3 kann allein schon wegen den unterschiedlichen Einheiten von $s_i(t)$ und $\varphi_{\it j}(t)$ nicht stimmen. Die Signale weisen wie $A$ die Einheit $\sqrt{\rm W}$ auf, die Basisfunktionen die Einheit $\sqrt{\rm 1/s}$. | ||
| + | |||
| + | * Richtig ist somit die letzte Lösungsalternative, wobei für $K$ gilt: | ||
:$$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$ | :$$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 13. Juli 2022, 17:41 Uhr
Diese Aufgabe verfolgt das genau gleiche Ziel wie die "Aufgabe 4.1":
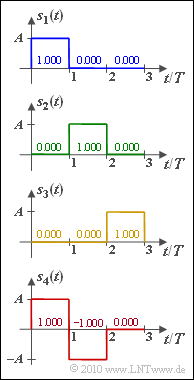
Für $M = 4$ energiebegrenzte Signale $s_i(t)$ mit $i = 1, \ \text{...} \ , 4$ sollen die $N$ erforderlichen orthonormalen Basisfunktionen $\varphi_{\it j}(t)$ gefunden werden, die folgende Bedingung erfüllen müssen:
- $$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$
Mit $M$ Sendesignale $s_i(t)$ können bereits weniger Basisfunktionen $\varphi_{\it j}(t)$ ausreichen, nämlich $N$. Allgemein gilt also $N ≤ M$.
Es handelt sich hier um die genau gleichen energiebegrenzten Signale $s_i(t)$ wie in der "Aufgabe 4.1":
- Der Unterschied ist die unterschiedliche Reihenfolge der Signale $s_i(t)$.
- Diese sind in dieser Aufgabe so sortiert, dass die Basisfunktionen auch ohne Anwendung des umständlicheren "Gram–Schmidt–Verfahrens" gefunden werden können.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Signale, Basisfunktionen und Vektorräume".
- Verwenden Sie für numerische Berechnungen $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $
Fragebogen
Musterlösung
- Damit ist offensichtlich, dass auch hier $\underline {N = 3}$ gelten muss.
(2) Die "2–Norm" gibt die Wurzel aus der Signalenergie an und ist vergleichbar mit dem Effektivwert bei leistungsbegrenzten Signalen.
- Die ersten drei Signale haben alle die "2–Norm"
- $$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
- Die Norm des letzten Signals ist um den Faktor $\sqrt{2}$ größer:
- $$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
(3) Die erste und die letzte Aussage sind zutreffend im Gegensatz zu den Aussagen 2 und 3:
- Es wäre völlig unlogisch, wenn die gefundenen Basisfunktionen bei anderer Sortierung der Signale $s_i(t)$ nicht mehr gelten sollten.
- Das Gram–Schmidt–Verfahren liefert nur einen möglichen Basisfunktionssatz $\{\varphi_{\it j}(t)\}$. Bei anderer Sortierung ergibt sich (möglicherweise) ein anderer.
- Die Anzahl der Permutationen von $M = 4$ Signalen ist "$4! = 24$". Mehr Basisfunktionssätze kann es auf keinen Fall geben ⇒ der Lösungsvorschlag 2 ist falsch.
- Wahrscheinlich gibt es (wegen $N = 3$) aber nur "$3! = 6$" mögliche Basisfunktionssätze.
- Wie aus der Musterlösung zur Aufgabe 4.1 ersichtlich ist, werden sich mit der Reihenfolge $s_1(t),\ s_2(t),\ s_4(t),\ s_3(t)$ die gleichen Basisfunktionen ergeben wie mit $s_1(t),\ s_2(t),\ s_3(t),\ s_4(t)$. Dies ist aber nur eine Vermutung der Autoren; wir haben es nicht überprüft.
- Die Aussage 3 kann allein schon wegen den unterschiedlichen Einheiten von $s_i(t)$ und $\varphi_{\it j}(t)$ nicht stimmen. Die Signale weisen wie $A$ die Einheit $\sqrt{\rm W}$ auf, die Basisfunktionen die Einheit $\sqrt{\rm 1/s}$.
- Richtig ist somit die letzte Lösungsalternative, wobei für $K$ gilt:
- $$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$
(4) Aus dem Vergleich der Diagramme auf der Angabenseite erkennt man:
- $$s_{4}(t) = s_{1}(t) - s_{2}(t) = K \cdot \varphi_1(t) - K \cdot \varphi_2(t)\hspace{0.05cm}.$$
- Weiterhin gilt:
- $$s_{4}(t) = s_{41}\cdot \varphi_1(t) + s_{42}\cdot \varphi_2(t) + s_{43}\cdot \varphi_3(t)$$
- $$\Rightarrow \hspace{0.3cm}s_{41} = K \hspace{0.1cm}\hspace{0.15cm}\underline {= 10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{42} = -K \hspace{0.1cm}\hspace{0.15cm}\underline {= -10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 0}\hspace{0.05cm}. $$