Aufgaben:Aufgabe 3.5Z: Phasenmodulation eines Trapezsignals: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Frequenzmodulation (FM) }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |t…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1100__Mod_Z_3_5.png|right|]] |
| + | Ein Phasenmodulator mit dem Eingangssignal $q_1(t)$ und dem modulierten Signal $s(t)$ am Ausgang wird durch folgende Gleichung beschrieben: | ||
| + | $$s(t) = A_{\rm T} \cdot \cos (\psi(t) )=$$ | ||
| + | $$ = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q_1(t) ) \hspace{0.05cm}.$$ | ||
| + | Die Trägerkreisfrequenz beträgt $ω_T = 2π · 10^5 \frac{1}{s}$. Berücksichtigen Sie bei der Lösung dieser Aufgabe, dass die Augenblickskreisfrequenz $ω_A(t)$ stets gleich der Ableitung der Winkelfunktion $ψ(t)$ nach der Zeit ist. Die Augenblicksfrequenz ist $f_A(t) = ω_A(t)/2π$. | ||
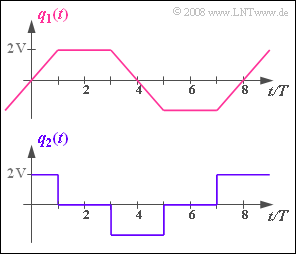
| + | Als Testsignal wird das oben skizzierte Trapez–Signal $q1(t)$ angelegt, wobei die Nomierungszeitdauer $T = 10 μs$ beträgt. | ||
| + | Zum gleichen modulierten Signal $s(t)$ würde ein Frequenzmodulator mit der Winkelfunktion | ||
| + | $$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q_2(t)\hspace{0.15cm}{\rm d}t$$ | ||
| + | führen, wenn das rechteckförmige Quellensignal $q_2(t)$ entsprechend der unteren Skizze angelegt wird. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://www.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1] und [http://www.lntwww.de/Modulationsverfahren/Frequenzmodulation_(FM) Kapitel 3.2]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie ist die Modulatorkonstante $K_{PM}$ zu wählen, damit $ϕ_{max} = 3 rad$ beträgt? |
| − | |type=" | + | |type="{}"} |
| − | + | $K_{PM}$ = { 1.5 3% } $V^{-1}$ | |
| − | + | ||
| + | |||
| + | {Welche Werte nimmt die Augenblicksfrequenz $f_A(t)$ im Bereich $0 < t < T | ||
| + | $ an? | ||
| + | |type="{}"} | ||
| + | $ 0 ... T: f_{A, min }$ = { 147.7 3% } $KHz$ | ||
| + | $ 0 ... T: f_{A, max }$ = { 147.7 3% } $KHz$ | ||
| + | |||
| + | {Welche Werte nimmt die Augenblicksfrequenz $f_A(t)$ im Bereich $T < t < 3T$ an? | ||
| + | |type="{}"} | ||
| + | $ T ... 3T: f_{A, min }$ = { 100 3% } $KHz$ | ||
| + | $ T ... 3T: f_{A, max }$ = { 100 3% } $KHz$ | ||
| + | {Welche Werte besitzt die Augenblicksfrequenz $f_A(t)$ im Bereich $3T < t < 5T$? | ||
| + | |type="{}"} | ||
| + | $ 3T ... 5T: f_{A, min }$ = { 52.3 3% } $KHz$ | ||
| + | $ 3T ... 5T: f_{A, max }$ = { 52.3 3% } $KHz$ | ||
| − | { | + | {Wie muss die Modulatorkonstante $K_{FM}$ gewählt werden, damit das Signal $q_2(t)$ nach Frequenzmodulation zum gleichen HF–Signal $s(t)$ führt? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $K_{FM}$ = { 1.5 3% } $V^{-1}s^{-1}$ |
| Zeile 25: | Zeile 50: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Die Phasenfunktion berechnet sich zu $ϕ(t) = K_{PM} · q_1(t)$. Der Phasenhub $ϕ_{max}$ ist gleich der sich ergebenden Phase für den Maximalwert des Quellensignals: |
| − | '''2.''' | + | $$ \phi_{\rm max} = K_{\rm PM} \cdot 2\,{\rm V} = 3\,{\rm rad}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm PM} \hspace{0.15cm}\underline {= 1.5\,{\rm V^{-1}}} \hspace{0.05cm}.$$ |
| − | '''3.''' | + | |
| − | '''4.''' | + | |
| − | '''5.''' | + | '''2.''' Im Bereich von 0 bis T kann die Winkelfunktion wie folgt dargestellt werden: |
| − | + | $$ \psi(t) = \omega_{\rm T} \cdot t + K_{\rm PM} \cdot 2\,{\rm V} \cdot {t}/{T}\hspace{0.05cm}.$$ | |
| − | + | Für die Augenblickskreisfrequenz $ω_A(t)$ bzw. die Augenblicksfrequenz $f_A(t)$ gilt dann: | |
| + | $$\omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}= \omega_{\rm T} + K_{\rm PM} \cdot \frac{2\,{\rm V}}{10\,{\rm \mu s}}\hspace{0.05cm}$$ | ||
| + | $$\Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T} + \frac{1.5\,{ V}^{-1}}{2 \pi} \cdot 2 \cdot 10^5 {V}/{ s} = 100\,{\rm kHz}+ 47.7\,{\rm kHz}= 147.7\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | Die Augenblicksfrequenz ist konstant, so dass $f_{A, min} = f_{A, max} = 147.7 kHz$ gilt. | ||
| + | |||
| + | |||
| + | '''3.''' Aufgrund des konstanten Quellensignals ist im gesamten hier betrachteten Zeitbereich ($T ... 3T$) die Ableitung gleich 0, so dass die Augenblicksfrequenz gleich der Trägerfrequenz ist: | ||
| + | $$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} \hspace{0.15cm}\underline {= 100\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''4.''' Der lineare Abfall von $q_1(t)$ in diesem Zeitintervall ($3T ... 5T$) mit betragsmäßig gleicher Steigung, wie unter Punkt b) berechnet, führt zum Ergebnis: | ||
| + | $$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} - 47.7\,{\rm kHz} \hspace{0.15cm}\underline {= 52.3\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''5.''' Durch Differentiation kommt man zur Augenblickskreisfrequenz: | ||
| + | $$ \omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q_2(t) \Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T}+\frac{ K_{\rm FM}}{2 \pi} \cdot q_2(t)\hspace{0.05cm}.$$ | ||
| + | Mit dem Ergebnis aus b) ergibt sich somit: | ||
| + | $$\frac{ K_{\rm FM}}{2 \pi} \cdot 2\,{\rm V} = \frac{ 3 \cdot 10^5}{2 \pi} \cdot {\rm s^{-1}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} \hspace{0.15cm}\underline {= 1.5 \cdot 10^5 \hspace{0.15cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 3. Januar 2017, 17:13 Uhr
Ein Phasenmodulator mit dem Eingangssignal $q_1(t)$ und dem modulierten Signal $s(t)$ am Ausgang wird durch folgende Gleichung beschrieben: $$s(t) = A_{\rm T} \cdot \cos (\psi(t) )=$$ $$ = A_{\rm T} \cdot \cos (\omega_{\rm T} \cdot t + K_{\rm PM} \cdot q_1(t) ) \hspace{0.05cm}.$$ Die Trägerkreisfrequenz beträgt $ω_T = 2π · 10^5 \frac{1}{s}$. Berücksichtigen Sie bei der Lösung dieser Aufgabe, dass die Augenblickskreisfrequenz $ω_A(t)$ stets gleich der Ableitung der Winkelfunktion $ψ(t)$ nach der Zeit ist. Die Augenblicksfrequenz ist $f_A(t) = ω_A(t)/2π$.
Als Testsignal wird das oben skizzierte Trapez–Signal $q1(t)$ angelegt, wobei die Nomierungszeitdauer $T = 10 μs$ beträgt.
Zum gleichen modulierten Signal $s(t)$ würde ein Frequenzmodulator mit der Winkelfunktion $$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q_2(t)\hspace{0.15cm}{\rm d}t$$ führen, wenn das rechteckförmige Quellensignal $q_2(t)$ entsprechend der unteren Skizze angelegt wird.
Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.1 und Kapitel 3.2.
Fragebogen
Musterlösung
2. Im Bereich von 0 bis T kann die Winkelfunktion wie folgt dargestellt werden:
$$ \psi(t) = \omega_{\rm T} \cdot t + K_{\rm PM} \cdot 2\,{\rm V} \cdot {t}/{T}\hspace{0.05cm}.$$
Für die Augenblickskreisfrequenz $ω_A(t)$ bzw. die Augenblicksfrequenz $f_A(t)$ gilt dann:
$$\omega_{\rm A}(t) = \frac{{\rm d}\hspace{0.03cm}\psi(t)}{{\rm d}t}= \omega_{\rm T} + K_{\rm PM} \cdot \frac{2\,{\rm V}}{10\,{\rm \mu s}}\hspace{0.05cm}$$
$$\Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T} + \frac{1.5\,{ V}^{-1}}{2 \pi} \cdot 2 \cdot 10^5 {V}/{ s} = 100\,{\rm kHz}+ 47.7\,{\rm kHz}= 147.7\,{\rm kHz}\hspace{0.05cm}.$$
Die Augenblicksfrequenz ist konstant, so dass $f_{A, min} = f_{A, max} = 147.7 kHz$ gilt.
3. Aufgrund des konstanten Quellensignals ist im gesamten hier betrachteten Zeitbereich ($T ... 3T$) die Ableitung gleich 0, so dass die Augenblicksfrequenz gleich der Trägerfrequenz ist:
$$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} \hspace{0.15cm}\underline {= 100\,{\rm kHz}}\hspace{0.05cm}.$$
4. Der lineare Abfall von $q_1(t)$ in diesem Zeitintervall ($3T ... 5T$) mit betragsmäßig gleicher Steigung, wie unter Punkt b) berechnet, führt zum Ergebnis: $$f_{\rm A, \hspace{0.05cm} min} =f_{\rm A, \hspace{0.05cm} max} =f_{\rm T} - 47.7\,{\rm kHz} \hspace{0.15cm}\underline {= 52.3\,{\rm kHz}}\hspace{0.05cm}.$$
5. Durch Differentiation kommt man zur Augenblickskreisfrequenz: $$ \omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q_2(t) \Rightarrow \hspace{0.3cm} f_{\rm A}(t) = f_{\rm T}+\frac{ K_{\rm FM}}{2 \pi} \cdot q_2(t)\hspace{0.05cm}.$$ Mit dem Ergebnis aus b) ergibt sich somit: $$\frac{ K_{\rm FM}}{2 \pi} \cdot 2\,{\rm V} = \frac{ 3 \cdot 10^5}{2 \pi} \cdot {\rm s^{-1}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} \hspace{0.15cm}\underline {= 1.5 \cdot 10^5 \hspace{0.15cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$