Aufgaben:Aufgabe 3.2: Spektrum bei Winkelmodulation: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Phasenmodulation (PM) }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |typ…“) |
Safwen (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID1081__Mod_A_3_2.png|right|]] |
| + | Es wird hier von folgenden Gleichungen ausgegangen: | ||
| + | :* Quellensignal: | ||
| + | $$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| + | :* Sendesignal: | ||
| + | $$s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + K \cdot q(t))\hspace{0.05cm},$$ | ||
| + | :* idealer Kanal, d.h. das Empfangssignal: | ||
| + | $$r(t) = s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t))\hspace{0.05cm},$$ | ||
| + | :* idealer Demodulator; | ||
| + | $$ v(t) = \frac{1}{ K} \cdot \phi(t)\hspace{0.05cm}.$$ | ||
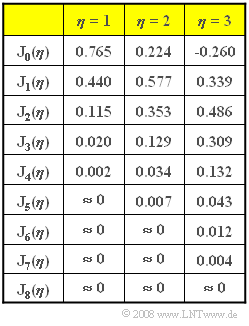
| + | Die Grafik zeigt die Besselfunktionen erster Art und n-ter Ordnung in tabellarischer Form. | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe bezieht sich auf den Theorieteil von [http://www.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1]. | ||
| Zeile 9: | Zeile 21: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welches Modulationsverfahren liegt hier vor? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Amplitudenmodulation. |
| − | + | + | + Phasenmodulation. |
| + | - Frequenzmodulation. | ||
| + | {Welches Modulationsverfahren würden Sie wählen, wenn die Kanalbandbreite $B_K = 10 kHz$ betragen würde? | ||
| + | |type="[]"} | ||
| + | + Amplitudenmodulation. | ||
| + | - Phasenmodulation. | ||
| + | - Frequenzmodulation. | ||
| − | { | + | {Wie ist die Modulatorkonstante zu wählen, damit der Phasenhub $η = 1$ beträgt? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $K$ = { 0.5 3% } $1/V$ |
| + | {Berechnen Sie das Spektrum $S_{TP}(f)$ des äquivalenten Tiefpass–Signals. Wie groß sind die Gewichte der Spektrallinien bei $f = 0$ und $f = –3 kHz$? | ||
| + | |type="{}"} | ||
| + | $S_{TP}(f = 0)$ = { 0.765 3% } $V$ | ||
| + | $S_{TP}(f = -3 KHz)$ = { -0.44 3% } $V$ | ||
| + | {Berechnen Sie die Spektren des analytischen Signals sowie des physikalischen Signals. Wie groß sind die Gewichte der Spektrallinien bei 97 kHz? | ||
| + | |type="{}"} | ||
| + | $S_+(f = 97 kHz)$ = { -0.44 3% } $V$ | ||
| + | $S(f = 97 kHz)$ = { -0.22 3% } $V$ | ||
| + | |||
| + | |||
| + | {Wie groß ist die erforderliche Kanalbandbreite $B_K$, wenn man (betragsmäßige) Impulsgewichte kleiner als 0.01 vernachlässigt? | ||
| + | |type="{}"} | ||
| + | $ η = 1 : B_K$ = { 18 3% } $KHz$ | ||
| + | |||
| + | {Welche Kanalbandbreiten würden sich für $η = 2$ und $η = 3$ ergeben? | ||
| + | |type="{}"} | ||
| + | $η = 2 : B_K$ = { 24 3% } $KHz$ | ||
| + | $η = 3 : B_K$ = { 36 3% } $KHz$ | ||
</quiz> | </quiz> | ||
| Zeile 25: | Zeile 61: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.'''Es handelt sich um eine Phasenmodulation: Die Phase $ϕ(t)$ ist proportional zum Quellensignal $q(t)$ ⇒ Antwort 2. |
| − | '''2.''' | + | |
| − | '''3.''' | + | '''2.''' Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal zu nichtlinearen Verzerrungen. Bei AM ist dagegen bereits mit $B_K = 6 kHz$ eine verzerrungsfreie Übertragung möglich ⇒ Antwort 1. |
| − | '''4.''' | + | |
| − | '''5.''' | + | '''3.''' Der Modulationsindex (oder Phasenhub) ist bei PM gleich $η = K · A_N$. Somit ist $K = 1/A_N = 0.5 1/V$ zu wählen, damit sich $η = 1$ ergibt. |
| − | '''6.''' | + | |
| − | '''7.''' | + | |
| + | '''4.''' Es liegt ein sogenanntes Besselspektrum vor: | ||
| + | $$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$ | ||
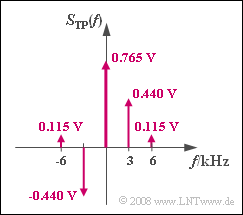
| + | Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_N$, wobei n ganzzahlig ist. Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_T = 1 V$ erhält man: | ||
| + | [[Datei:P_ID1082__Mod_A_3_2_d.png|right|]] | ||
| + | $$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ | ||
| + | $$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ | ||
| + | $$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ | ||
| + | Aufgrund der Symmetrieeigenschaft | ||
| + | $${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$$ | ||
| + | erhält man für die Spektrallinie bei $f = –3 kHz$: | ||
| + | $$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ | ||
| + | ''Anmerkung'': Eigentlich müsste man für den Spektralwert bei f = 0 schreiben: | ||
| + | $$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | ||
| + | Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich. Gleiches gilt für alle diskreten Spektrallinien. | ||
| + | |||
| + | |||
| + | '''5.'''$S_+(f)$ ergibt sich aus $S_{TP}(f)$ durch Verschiebung um $f_T$ nach rechts. Deshalb ist | ||
| + | $$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | ||
| + | Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor 1/2: | ||
| + | $$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | ||
| + | Allgemein kann geschrieben werden: | ||
| + | $$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''6.''' Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien $J_{|n|>3}$ außer Acht gelassen werden. Damit erhält man $B_K = 2 · 3 · f_N = 18 kHz$. | ||
| + | |||
| + | '''7.''' Die Zahlenwerte in der Tabelle auf der Angabenseite zeigen, dass nun $B_K = 24 kHz$ (für $η = 2$) bzw. $B_K = 36 kHz$ (für $η = 3$) erforderlich wären. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Version vom 2. Januar 2017, 16:27 Uhr
Es wird hier von folgenden Gleichungen ausgegangen:
- Quellensignal:
$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- Sendesignal:
$$s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + K \cdot q(t))\hspace{0.05cm},$$
- idealer Kanal, d.h. das Empfangssignal:
$$r(t) = s(t) = 1\,{\rm V} \cdot \cos(2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t))\hspace{0.05cm},$$
- idealer Demodulator;
$$ v(t) = \frac{1}{ K} \cdot \phi(t)\hspace{0.05cm}.$$ Die Grafik zeigt die Besselfunktionen erster Art und n-ter Ordnung in tabellarischer Form.
Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 3.1.
Fragebogen
Musterlösung
2. Eine Winkelmodulation (PM, FM) führt bei bandbegrenztem Kanal zu nichtlinearen Verzerrungen. Bei AM ist dagegen bereits mit $B_K = 6 kHz$ eine verzerrungsfreie Übertragung möglich ⇒ Antwort 1.
3. Der Modulationsindex (oder Phasenhub) ist bei PM gleich $η = K · A_N$. Somit ist $K = 1/A_N = 0.5 1/V$ zu wählen, damit sich $η = 1$ ergibt.
4. Es liegt ein sogenanntes Besselspektrum vor:
$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$
Dieses ist ein diskretes Spektrum mit Anteilen bei $f = n · f_N$, wobei n ganzzahlig ist. Die Gewichte der Diracfunktionen sind durch die Besselfunktionen gegeben. Mit $A_T = 1 V$ erhält man:
$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ $$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ $$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ Aufgrund der Symmetrieeigenschaft $${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$$ erhält man für die Spektrallinie bei $f = –3 kHz$: $$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ Anmerkung: Eigentlich müsste man für den Spektralwert bei f = 0 schreiben: $$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ Dieser ist somit aufgrund der Diracfunktion unendlich groß, lediglich das Gewicht der Diracfunktion ist endlich. Gleiches gilt für alle diskreten Spektrallinien.
5.$S_+(f)$ ergibt sich aus $S_{TP}(f)$ durch Verschiebung um $f_T$ nach rechts. Deshalb ist
$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$
Das tatsächliche Spektrum unterscheidet sich von $S_+(f)$ bei positiven Frequenzen um den Faktor 1/2:
$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$
Allgemein kann geschrieben werden:
$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$
6. Unter der vorgeschlagenen Vernachlässigung können alle Bessellinien $J_{|n|>3}$ außer Acht gelassen werden. Damit erhält man $B_K = 2 · 3 · f_N = 18 kHz$.
7. Die Zahlenwerte in der Tabelle auf der Angabenseite zeigen, dass nun $B_K = 24 kHz$ (für $η = 2$) bzw. $B_K = 36 kHz$ (für $η = 3$) erforderlich wären.