Aufgabe 2.12: Decodierung beim RSC (7, 4, 4) zur Basis 8

ELP–Belegungsschemata für $r = 1, \ r = 2, \ r = 3$

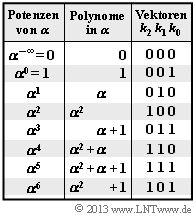
Wir analysieren den Peterson–Algorithmus, der im Abschnitt Vorgehensweise beim „Bounded Distance Decoding„ ausführlich dargelegt ist. Vorausgesetzt wird der Reed–Solomon–Code mit den Parametern $n = 7, \ k = 4$ und $d_{\rm min} = 4$, wobei alle Codesymbole aus $\rm GF(2^3)$ stammen und alle Rechenoperationen in $\rm GF(2^3)$ durchzuführen sind.

Die Prüfmatrix dieses Codes lautet:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

Im Schritt (A) des hier betrachteten Decodier–Algorithmus' muss das Syndrom $\underline{s} = \underline{y} \cdot \mathbf{H}^{\rm T}$ berechnet werden. Für das hier vorausgesetzte Empfangswort $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$ ergibt sich das Syndrom zu $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6)$, wie in der Aufgabe 2.12Z noch gezeigt wird.

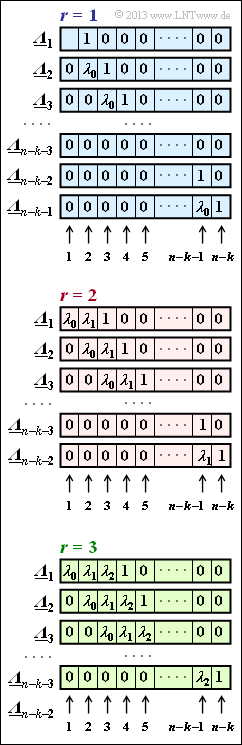
Danach müssen die ELP–Koeffizientenvektoren gemäß der nebenstehenden Abbildung aufgestellt und ausgewertet werden, wobei die Belegung davon abhängt, ob man von $r = 1, \ r = 2$ oder $r = 3$ Symbolfehlern im Empfangswort ausgeht. „ELP” steht für Error Locator Polynom.

Sind für die angenommene Symbolfehlerzahl $r$ alle Gleichungen ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ erfüllt, so weist das Empfangswort $\underline{y}$ tatsächlich genau $r$ Symbolfehler auf.

Die weiteren Schritte können Sie dem Theorieteil entnehmen:

Schritt (C): Lokalisierung der Fehlerpositionen,
Schritt (D): Ermittlung der Fehlerwerte.

Hinweise:

Die Aufgabe bezieht sich auf das Kapitel Fehlerkorrektur nach Reed–Solomon–Codierung.

Fragebogen

Musterlösung

(1) Richtig ist der Lösungsvorschlag 1:

Der betrachtete Reed–Solomon–Code $(7, \, 4, \, 4)_8$ kann wegen $d_{\rm min} = 4$ nur $t = ⌊(d_{\rm min} - 1)/2⌋ = 1$ Symbolfehler korrigieren.
Relevant ist also nur das blau hinterlegte Schema, das für den Fall gilt, dass es genau einen Symbolfehler im Empfangswort gibt $(r = 1)$.

(2) Entsprechend der Grafik auf der Angabenseite besitzt der Vektor ${\it \underline{\Lambda}}_l$ hier $L = n - k \ \underline{= 3}$ Elemente.

(3) Es gibt nur die beiden ELP–Koeffizientenvektoren ${\it \underline{\Lambda}}_1 = (\lambda_0, \, 1, \, 0)$ und ${\it \underline{\Lambda}}_2 = (0, \, \lambda_0, \, 1) \ \Rightarrow \ l_{\rm max} \ \underline{= 2}$.

(4) Aus ${\it \underline{\Lambda}}_1$ und ${\it \underline{\Lambda}}_2$ ergeben sich zwei skalare Bestimmungsgleichungen ${\it \underline{\Lambda}}_l \cdot \underline{s}^{\rm T} = 0$ für den Parameter $\lambda_0$:

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 \cdot \alpha^4 = -\alpha^5 = \alpha^5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^5 + \alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

Das Gleichungssystem ist eindeutig lösbar ⇒ Antwort JA.

(5) Mit dem Ergebnis der Teilaufgabe (4) ⇒ $\lambda_0 = \alpha$ erhält man für das Error Locator Polynom

$${\it \Lambda}(x)=x \cdot \big ({\it \lambda}_0 + x \big ) =x \cdot \big (\alpha + x )$$

$$\Rightarrow \hspace{0.3cm} {\it \Lambda}(\alpha^0 )\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot \big ( \alpha + 1 \big ) = \alpha + 1 \ne 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Keine\hspace{0.15cm} Nullstelle}\hspace{0.05cm},$$

$$\hspace{0.875cm} {\it \Lambda}(\alpha^1)\hspace{-0.15cm} \ = \ \hspace{-0.15cm}\alpha \cdot \big (\alpha + \alpha\big ) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Nullstelle}}\hspace{0.05cm}.$$

Verfälscht wurde also das Symbol an der Position 1 ⇒ Lösungsvorschlag 2. Da die Berechnung in der Teilaufgabe (4) unter der Bedingung $r = 1$ erfolgte, wurden alle anderen Symbole richtig übertragen:

Umrechnungstabellen für das Galoisfeld $\rm GF(2^3)$

$$\underline {e} = (0, e_1, 0, 0, 0, 0, 0)\hspace{0.05cm}. $$

(6) Aus der Bedingung $\underline{e} \cdot \mathbf{H}^{\rm T} = \underline{s}^{\rm T}$ folgt

$$(0, e_1, 0, 0, 0, 0, 0) \cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12} \\ \alpha^5 & \alpha^{10} & \alpha^{15} \\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\stackrel{!}{=} \hspace{0.15cm} \begin{pmatrix} \alpha^4\\ \alpha^5\\ \alpha^6 \end{pmatrix} $$

$$\Rightarrow \hspace{0.3cm} e_1 \cdot \alpha = \alpha^4\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.4cm} e_1 \cdot \alpha^3 = \alpha^6\hspace{0.05cm}. $$

Die Lösung führt stets zum Ergebnis $e_1 = \alpha^3$ ⇒ Antwort 2.
Mit dem Empfangswort $\underline{y} = (\alpha^1, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$ erhält man das Decodierergebnis $\underline{z} = (\alpha^1, \, \alpha^3, \, \alpha^3, \, 0, \, 1, \, \alpha^1, \, 0)$.

(7) Analog zur Teilaufgabe (4) lautet nun das Gleichungssystem:

$$\lambda_0 \cdot \alpha^2 + \alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^2 \hspace{0.05cm},$$

$$\lambda_0 \cdot \alpha^4 + \alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha \hspace{0.05cm}.$$

Die beiden Lösungen widersprechen sich. Bei der Übertragung müssen also mindestens zwei Symbole verfälscht worden sein und die Decodierung versagt ⇒ Antwort NEIN. Man müsste nun einen neuen Versuch gemäß dem roten Schema $(r = 2)$ starten.

	Das blau hinterlegte Schema $(r = 1)$.
	Das rot hinterlegte Schema $(r = 2)$.
	Das grün hinterlegte Schema $(r = 3)$.

	$e_i = \alpha^2$,
	$e_i = \alpha^3$,
	$e_i = 1$.