Aufgabe 2.12Z: Reed–Solomon–Syndromberechnung

• Zurück zum Buch

Umrechnungstabelle für das Galoisfeld  $\rm GF(2^3)$

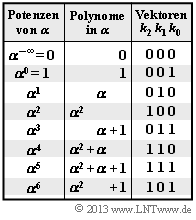
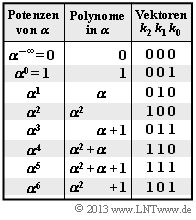
Wie in der  "Aufgabe 2.12"  betrachten wir den Reed–Solomon–Code  $(7, \, 4, \, 4)_8$,  der auf dem Galoisfeld   ${\rm GF}(q)$   mit  $q = 8 = 2^3$  basiert.  Die Grafik zeigt die zugehörige Umrechnungstabelle.

Gegeben sind die möglichen Codesymbole in

1. Exponentendarstellung $($Potenzen von  $\alpha)$ 
2. Polynomdarstellung
3. Koeffizientenvektordarstellung.

Vorgegeben ist das Empfangswort   $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$.

• Anhand des Syndroms  $\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$   soll überprüft werden,  ob einzelne Symbole des Empfangsvektors   $\underline{y}$   bei der Übertragung verfälscht wurden.

• Gegeben ist hierzu die Prüfmatrix  $\mathbf{H}$  des betrachteten Codes und deren Transponierte:

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H}}^{\rm T} = \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

Hinweis:  Die Aufgabe bezieht sich auf die Seite  "Schritt  $\rm (A)$: Auswertung des Syndroms beim BDD"  des Kapitels  "Fehlerdeccodierung nach Reed–Solomon–Codierung".

Fragebogen

1

Empfangen wurde das Wort   $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$.  Geben Sie das erste Element des Syndroms  $\underline{s} = (s_0, \, s_1, \, s_2)$  an.

	$s_0 = \alpha^4$,
	$s_0 = \alpha^5$,
	$s_0 = \alpha^6$,
	$s_0 = 0, \, 1, \, \alpha, \, \alpha^2$  oder  $\alpha^3$.

2

Wie lautet bei gleichem Empfangswort das zweite Syndromelement?

	$s_1 = \alpha^4$,
	$s_1 = \alpha^5$,
	$s_1 = \alpha^6$,
	$s_1 = 0, \, 1, \, \alpha, \, \alpha^2$  oder  $\alpha^3$.

3

Wie lautet bei gleichem Empfangswort das dritte Syndromelement?

	$s_2 = \alpha^4$,
	$s_2 = \alpha^5$,
	$s_2 = \alpha^6$,
	$s_2 = 0, \, 1, \, \alpha, \, \alpha^2$ oder $\alpha^3$.

4

Bekannt ist,  dass das vorliegende Empfangswort  $\underline{y}$  richtig decodiert werden kann.  Wieviele Symbolfehler beinhaltet dieses Empfangswort?

$r \ = \ $

Musterlösung

Musterlösung

Umrechnungstabellen für das Galoisfeld  $\rm GF(2^3)$

(1)  Die entsprechende Gleichung zur Syndromberechnung lautet:

$$\underline {s} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (s_0, s_1, s_2) = \begin{pmatrix} \alpha,0, \alpha^3,0, 1, \alpha,0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

• Das erste Element ergibt sich zu

$$s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^2 + 1 \cdot \alpha^4 + \alpha \cdot \alpha^5= \alpha + \alpha^5 + \alpha^4+ \alpha^6$$

$$\Rightarrow\hspace{0.3cm} s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\alpha) + (\alpha^2 + \alpha+ 1)+ (\alpha^2 + \alpha) + + (\alpha^2 + 1) = \alpha^2 + \alpha = \alpha^4\hspace{0.05cm}.$$

• Richtig ist der  Lösungsvorschlag 1.

(2)  Entsprechend gilt für das zweite Syndromelement entsprechend dem  Lösungsvorschlag 2:

$$s_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^4 + 1 \cdot \alpha^1 + \alpha \cdot \alpha^3= \alpha + \alpha^7 + \alpha+ \alpha^4= 1 + \alpha^4 = \alpha^2 + \alpha + 1 = \alpha^5 \hspace{0.05cm}.$$

(3)  Zur Berechnung von  $s_2$  muss das Empfangswort mit der letzten Matrixspalte multipliziert werden:

$$s_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^6 + 1 \cdot \alpha^5 + \alpha \cdot \alpha^1= \alpha + \alpha^2 + \alpha^5 + \alpha^2=\alpha^5 + \alpha = (\alpha^2 + \alpha + 1) + \alpha = \alpha^2 + 1 = \alpha^5 \hspace{0.05cm}.$$

• Richtig ist der  Lösungsvorschlag 3.

(4)  Aufgrund des errechneten Syndroms  $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6) ≠ 0$  beinhaltet das Empfangswort mindestens einen Symbolfehler   ⇒   $r > 0$.

• Der vorliegende Reed–Solomon–Code  $(7, \, 4, \, 4)_8 \ \Rightarrow \ d_{\rm min} = 4$  kann nicht mehr als  $t = ⌊d_{\rm min}/2⌋ = 1$  Fehler korrigieren.

• Da das Empfangswort gemäß Angabe tatsächlich decodiert werden kann,  gilt  $\underline{r = 1}$.

• Ohne diese Angabe  "das Empfangswort kann decodiert werden"  wäre diese Teilaufgabe nicht lösbar.