Applets:Zur Verdeutlichung digitaler Filter: Unterschied zwischen den Versionen
Höfler (Diskussion | Beiträge) |
|||
| (32 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{ | + | {{LntAppletLinkDeEn|digitalFilters|digitalFilters_en}} |
| + | |||
| + | |||
| + | ==Programmbeschreibung== | ||
| + | <br> | ||
| + | Das Applet soll die Eigenschaften digitaler Filter verdeutlichen, wobei wir uns auf Filter der Ordnung $M=2$ beschränken. Behandelt werden sowohl nichtrekursive Filter $\rm (FIR$, ''Finite Impulse Response''$)$ als auch rekursive Filter $\rm (IIR$, ''Infinite Impulse Response''$)$. | ||
| + | |||
| + | Das Eingangssignal $x(t)$ wird durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht. Berechnet wird die Ausgangsfolge $〈y_ν〉$, also die zeitdiskrete Darstellung des Ausgangssignal $y(t)$. | ||
| + | |||
| + | *$T_{\rm A}$ bezeichnet den zeitlichen Abstand zwischen zwei Abtastwerten. | ||
| + | *Zudem beschränken uns auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ sowie $y_ν \equiv 0$ für $ν < 0$. | ||
| + | |||
| + | |||
| + | Weiter ist anzumerken: Wir bezeichnen die Ausgangsfolge $〈y_ν〉$ als | ||
| + | |||
| + | '''(1)''' die '''zeitdiskrete Impulsantwort''' $〈h_ν〉$, wenn am Eingang die „zeitdiskrete Diracfunktion” anliegt: $〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉,$ | ||
| + | |||
| + | '''(2)''' die '''zeitdiskrete Sprungantwort''' $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt: $〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 ,$ | ||
| + | |||
| + | '''(3)''' die '''zeitdiskrete Rechteckantwort''' $〈\rho_ν^{(2, 4)}〉$, wenn am Eingang die „zeitdiskrete Rechteckfunktion” anliegt: $〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 ;$<br> In Hochkommata angegeben sind hier der Beginn der Einsen $(\nu =2)$ und die Stelle der letzten Eins $(\nu =4)$. | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | + | ||
===Allgemeines Blockschaltbild=== | ===Allgemeines Blockschaltbild=== | ||
| − | + | ||
Jedes Signal $x(t)$ kann an einem Rechner nur durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt werden, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht. | Jedes Signal $x(t)$ kann an einem Rechner nur durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt werden, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht. | ||
| − | [[Datei:P_ID552__Sto_T_5_2_S1_neu.png |right|frame| Blockschaltbild eines digitalen (IIR–) Filters $M$ | + | [[Datei:P_ID552__Sto_T_5_2_S1_neu.png |right|frame| Blockschaltbild eines digitalen (IIR–) Filters der Ordnung $M$]] |
*Der zeitliche Abstand $T_{\rm A}$ zwischen zwei Abtastwerten ist dabei durch das [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Das_Abtasttheorem|Abtasttheorem]] nach oben begrenzt. | *Der zeitliche Abstand $T_{\rm A}$ zwischen zwei Abtastwerten ist dabei durch das [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Das_Abtasttheorem|Abtasttheorem]] nach oben begrenzt. | ||
| − | *Wir beschränken uns hier auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ für $ν | + | *Wir beschränken uns hier auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ für $ν < 0$. |
*Um den Einfluss eines linearen Filters mit Frequenzgang $H(f)$ auf das zeitdiskrete Eingangssignal $〈x_ν〉$ zu erfassen, bietet es sich an, auch das Filter zeitdiskret zu beschreiben. Im Zeitbereich geschieht das mit der zeitdiskreten Impulsantwort $〈h_ν〉$. | *Um den Einfluss eines linearen Filters mit Frequenzgang $H(f)$ auf das zeitdiskrete Eingangssignal $〈x_ν〉$ zu erfassen, bietet es sich an, auch das Filter zeitdiskret zu beschreiben. Im Zeitbereich geschieht das mit der zeitdiskreten Impulsantwort $〈h_ν〉$. | ||
| Zeile 16: | Zeile 35: | ||
Hierzu ist Folgendes zu bemerken: | Hierzu ist Folgendes zu bemerken: | ||
| − | *Der Index $\nu$ bezieht sich auf Folgen, zum Beispiel | + | *Der Index $\nu$ bezieht sich auf Folgen, zum Beispiel am Eingang $〈x_ν〉$ und Ausgang $〈y_ν〉$. |
*Den Index $\mu$ verwenden wir dagegen für die Kennzeichnung der $a$– und $b$–Filterkoeffizienten. | *Den Index $\mu$ verwenden wir dagegen für die Kennzeichnung der $a$– und $b$–Filterkoeffizienten. | ||
*Die erste Summe beschreibt die Abhängigkeit des aktuellen Ausgangs $y_ν$ vom aktuellen Eingang $x_ν$ und von den $M$ vorherigen Eingangswerten $x_{ν-1}$, ... , $x_{ν-M}.$ | *Die erste Summe beschreibt die Abhängigkeit des aktuellen Ausgangs $y_ν$ vom aktuellen Eingang $x_ν$ und von den $M$ vorherigen Eingangswerten $x_{ν-1}$, ... , $x_{ν-M}.$ | ||
| Zeile 30: | Zeile 49: | ||
'''(2)''' Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die '''zeitdiskrete Sprungantwort''' $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt: | '''(2)''' Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die '''zeitdiskrete Sprungantwort''' $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt: | ||
:$$〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 .$$ | :$$〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 .$$ | ||
| − | '''(3)''' Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die '''zeitdiskrete | + | '''(3)''' Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die '''zeitdiskrete Rechteckantwort''' $〈\rho_ν^{(2, 4)}〉$, wenn am Eingang die „zeitdiskrete Rechteckfunktion” anliegt: |
:$$〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 .$$ | :$$〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 .$$ | ||
| − | :In Hochkommata angegeben sind hier der Beginn der Einsen $(2)$ und die Stelle der letzten Eins $(4)$. | + | :In Hochkommata angegeben sind hier der Beginn der Einsen $(\nu =2)$ und die Stelle der letzten Eins $(\nu =4)$. |
}} | }} | ||
| − | ===Nichtrekursives Filter & | + | ===Nichtrekursives Filter ⇒ FIR–Filter === |
| − | + | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Sind alle Rückführungskoeffizienten $b_{\mu} = 0$, so spricht von einem '''nichtrekursiven Filter'''. | + | $\text{Definition:}$ Sind alle Rückführungskoeffizienten $b_{\mu} = 0$, so spricht von einem '''nichtrekursiven Filter'''. In der englischsprachigen Literatur ist hierfür auch die Bezeichnung '''FIR Filter''' (von „Finite Impulse Response”) gebräuchlich. |
| + | [[Datei:P_ID553__Sto_T_5_2_S2_neu.png|right |frame| Nichtrekursives digitales Filter $($FIR–Filter$)$ der Ordnung $M$]] | ||
Für die Ordnung $M$ gilt: | Für die Ordnung $M$ gilt: | ||
| Zeile 46: | Zeile 65: | ||
*Der Ausgangswert $y_ν$ hängt nur vom aktuellen und den $M$ vorherigen Eingangswerten ab: | *Der Ausgangswert $y_ν$ hängt nur vom aktuellen und den $M$ vorherigen Eingangswerten ab: | ||
:$$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu \cdot x_{\mu - \nu } } .$$ | :$$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu \cdot x_{\mu - \nu } } .$$ | ||
| − | * | + | *Zeitdiskrete Impulsantwort mit $〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉$: |
| − | :$$〈h_\ | + | :$$〈h_\nu〉= 〈a_0,\ a_1,\ \text{...} \ ,\ a_M〉 .$$ |
| + | *Aufgrund unserer Nomenklatur kann man die zeitdiskrete Impulsantwort auch mit $〈h_\mu〉= 〈a_0,\ a_1,\ \text{...} \ ,\ a_M〉 $ bezeichnen.}} | ||
| Zeile 61: | Zeile 81: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Betrachtet wird ein nichtrekursives Filter mit den Filterkoeffizienten $a_0 = 1,\hspace{0. | + | $\text{Beispiel 2:}$ Betrachtet wird ein nichtrekursives Filter mit den Filterkoeffizienten $a_0 = 1,\hspace{0.15cm} a_1 = 2,\hspace{0.15cm} a_2 = 1.$ |
| − | [[Datei:P_ID608__Sto_Z_5_3.png|right|frame|Nichtrekursives Filter]] | + | [[Datei:P_ID608__Sto_Z_5_3.png|right|frame|Nichtrekursives Filter $(M=2)$]] |
| − | '''(1)''' Die herkömmliche Impulsantwort lautet: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$ <br> ⇒ Zeitdiskrete Impulsantwort: $〈h_\mu〉= 〈1,\ 2,\ 1〉 . | + | '''(1)''' Die herkömmliche Impulsantwort lautet: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$ <br> ⇒ Zeitdiskrete Impulsantwort: $〈h_\mu〉= 〈1,\ 2,\ 1〉$. |
| − | '''(2)''' Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$. | + | '''(2)''' Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$. Nach Anwendung des Verschiebungssatzes: |
| − | :$$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }\cdot }f \cdot T_{\rm A} } )} \big ] \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm A} }\hspace{0.5cm}\Rightarrow \hspace{0.5cm}H(f = 0) = 4.$$ | + | :$$H(f) = 2 \cdot \big [ {1 + \cos ( {2{\rm{\pi }\cdot }f \cdot T_{\rm A} } )} \big ] \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm A} }\hspace{0.5cm}\Rightarrow \hspace{0.5cm}H(f = 0) = 4.$$ |
'''(3)''' Daraus folgt: Die '''zeitdiskrete Sprungantwort''' $〈\sigma_ν〉$ tendiert für große $\nu$ gegen $4$. | '''(3)''' Daraus folgt: Die '''zeitdiskrete Sprungantwort''' $〈\sigma_ν〉$ tendiert für große $\nu$ gegen $4$. | ||
| Zeile 75: | Zeile 95: | ||
'''(5)''' Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;1,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt | '''(5)''' Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;1,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt | ||
| − | :$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;3,\; | + | :$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;3,\;2,\;2,\;1,\;0,\;0,\;0,\;0,\;0,\; \text{...} \;} \right\rangle. $$}} |
| − | ===Rekursives Filter=== | + | ===Rekursives Filter ⇒ IIR–Filter === |
| − | + | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | $\text{Definition:}$ Sind alle Vorwärtskoeffizienten identisch $a_\ | + | [[Datei:P_ID607__Sto_A_5_3.png|right|frame|Rekursives Filter erster Ordnung]] |
| − | + | $\text{Definition:}$ | |
| + | *Ist zumindest einer der Rückführungskoeffizienten $b_{\mu} \ne 0$, so spricht von einem '''rekursiven Filter''' (siehe rechte Grafik). Insbesondere in der englischsprachigen Literatur ist hierfür auch die Bezeichnung '''IIR Filter''' (von „Infinite Impulse Response”) gebräuchlich. Dieser Filtertyp wird in der Verrsuchsdurchführung ausführlich behandelt. | ||
| + | |||
| + | *Sind zusätzlich alle Vorwärtskoeffizienten identisch $a_\mu = 0$ mit Ausnahme von $a_0$, so liegt ein '''rein rekursives Filter''' vor (siehe linke Grafik). | ||
| + | [[Datei:P_ID554__Sto_T_5_2_S3_neu.png|left|frame| Rein rekursives Filter erster Ordnung]] }} | ||
| − | + | Im Folgenden beschränken wir uns auf den Sonderfall „Rein rekursives Filter erster Ordnung”. Dieses Filter weist folgende Eigenschaften auf: | |
| − | Im Folgenden beschränken wir uns auf den Sonderfall | ||
*Der Ausgangswert $y_ν$ hängt (indirekt) von unendlich vielen Eingangswerten ab: | *Der Ausgangswert $y_ν$ hängt (indirekt) von unendlich vielen Eingangswerten ab: | ||
:$$y_\nu = \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot x_{\nu - \mu } .}$$ | :$$y_\nu = \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot x_{\nu - \mu } .}$$ | ||
*Dies zeigt die folgende Rechung: | *Dies zeigt die folgende Rechung: | ||
| − | :$$y_\nu = a_0 \cdot x_\nu + b_1 \cdot y_{\nu - 1} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + {b_1} ^2 \cdot y_{\nu - 2} | + | :$$y_\nu = a_0 \cdot x_\nu + b_1 \cdot y_{\nu - 1} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + {b_1} ^2 \cdot y_{\nu - 2} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + a_0 \cdot {b_1} ^2 \cdot x_{\nu - 2} + {b_1} ^3 \cdot y_{\nu - 3} = \text{...}. $$ |
| − | + | ||
| − | + | *Die zeitdiskrete Impulsantwort ist definitionsgemäß gleich der Ausgangsfolge, wenn am Eingang eine einzelne „Eins” bei $t =0$ anliegt. | |
| − | {{ | ||
| − | |||
| − | |||
| − | |||
:$$h(t)= \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )}\hspace{0.3cm} | :$$h(t)= \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )}\hspace{0.3cm} | ||
| − | \Rightarrow \hspace{0.3cm}〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉= 〈\hspace{0.05cm}a_0, \ a_0\cdot {b_1}, \ a_0\cdot {b_1}^2 \ \text{...} \hspace{0.05cm}〉.$$ | + | \Rightarrow \hspace{0.3cm}〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉= 〈\hspace{0.05cm}a_0, \ a_0\cdot {b_1}, \ a_0\cdot {b_1}^2, \ \text{...} \hspace{0.05cm}〉.$$ |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Fazit:}$ Bei einem rekursiven Filter reicht die (zeitdiskrete) Impulsantwort schon mit $M = 1$ bis ins Unendliche: | |
*Aus Stabilitätsgründen muss $b_1 < 1$ gelten. | *Aus Stabilitätsgründen muss $b_1 < 1$ gelten. | ||
| − | *Bei $b_1 = 1$ würde sich die Impulsantwort $h(t)$ bis ins Unendliche erstrecken und bei $b_1 > 1$ würde | + | *Bei $b_1 = 1$ würde sich die Impulsantwort $(h(t)$ bzw. $〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉)$ bis ins Unendliche erstrecken und bei $b_1 > 1$ würde sie sogar bis ins Unendliche anklingen. |
*Bei einem solchen rekursiven Filter erster Ordnung ist jede einzelne Diraclinie genau um den Faktor $b_1$ kleiner als die vorherige Diraclinie: | *Bei einem solchen rekursiven Filter erster Ordnung ist jede einzelne Diraclinie genau um den Faktor $b_1$ kleiner als die vorherige Diraclinie: | ||
| − | :$$h_{\mu} = h(\mu \cdot T_{\rm A}) = {b_1} \cdot h_{\mu -1}.$$ | + | :$$h_{\mu} = h(\mu \cdot T_{\rm A}) = {b_1} \cdot h_{\mu -1}.$$}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | + | {{GraueBox|TEXT= |
| − | = | + | [[Datei:Sto_T_5_2_S3_version2.png |frame| Zeitdiskrete Impulsantwort | rechts]] |
| + | $\text{Beispiel 3:}$ Die nebenstehende Grafik zeigt die zeitdiskrete Impulsantwort $〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉$ eines rekursiven Filters erster Ordnung mit den Parametern $a_0 = 1$ und $b_1 = 0.6$. | ||
| + | *Der (zeitdiskrete) Verlauf ist exponentiell abfallend und erstreckt sich bis ins Unendliche. | ||
| + | *Das Verhältnis der Gewichte zweier aufeinanderfolgender Diracs ist jeweils $b_1 = 0.6$. | ||
| + | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===Rekursives Filter als Sinus–Generator=== | ||
| + | Die Grafik zeigt ein digitales Filter zweiter Ordnung, das zur Erzeugung einer zeitdiskreten Sinusfunktion auf einem digitalen Signalprozessor $\rm (DSP)$ geeignet ist, wenn die Eingangsfolge $\left\langle \hspace{0.05cm} {x_\nu } \hspace{0.05cm}\right\rangle = = 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉$ eine (zeitdiskrete) Diracfunktion ist: | ||
| + | [[Datei:EN_Sto_A_5_4_version2.png|right|frame|Vorgeschlagene Filterstruktur]] | ||
| − | + | :$$\left\langle \hspace{0.05cm}{y_\nu }\hspace{0.05cm} \right\rangle = \left\langle {\, \sin ( {\nu \cdot T_{\rm A} \cdot \omega _0 } )\, }\right\rangle .$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die fünf Filterkoeffizienten ergeben sich aus der [https://de.wikipedia.org/wiki/Z-Transformation $Z$-Transformation]: | |
| + | :$$Z \big \{ {\sin ( {\nu T{\rm A}\cdot \omega _0 } )} \big \} = \frac{{z \cdot \sin \left( {\omega _0 \cdot T_{\rm A}} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 \cdot T_{\rm A}} \right) + 1}}.$$ | ||
| + | Nach Umsetzung dieser Gleichung durch ein rekursives Filter zweiter Ordnung erhält man folgende Filterkoeffizienten: | ||
| + | :$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 \cdot T_{\rm A}} \right),\quad a_2 = 0, \quad b_1 = 2 \cdot \cos \left( {\omega _0 \cdot T_{\rm A}} \right),\quad b_2 = - 1.$$ | ||
| − | * | + | *Auf die Filterkoeffizienten $a_0$ und $a_2$ kann verzichtet werden und $b_2=-1$ hat einen festen Wert. |
| − | + | *Die Kreisfrequenz $\omega_0$ der Sinusschwingung wird also nur durch $a_1$ und $b_1$ festelegt. | |
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 4:}$ Es gelte $a_1 = 0.5$, $b_1 = \sqrt 3$, $x_0 = 1$ und $x_{\nu \hspace{0.05cm}\ne\hspace{0.05cm} 0} = 0$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | ||
| − | $\text{ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | $ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(1)''' Dann gilt für die Ausgangswerte $y_\nu$ zu den Zeitpunkten $\nu \ge 0$:<br> | |
| − | + | :* $y_0 = 0;$ | |
| − | + | :* $y_1 = 0.5$ ⇒ die „$1$” am Eingang wirkt sich wegen $a_0= 0$ am Ausgang erst zum Zeitpunkt $\nu = 1$ aus; | |
| − | :$ | + | :* $y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \approx 0.866$ ⇒ bei $\nu = 2$ wird auch der rekursive Teil des Filters wirksam; |
| − | + | :* $y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1$ ⇒ für $\nu \ge 2$ ist das Filter rein rekursiv: $y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2}$; | |
| − | :$ | + | :* $y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$ |
| − | : | + | :* $y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = 0.5;$ |
| + | :* $y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$ | ||
| + | :* $y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} = - 0.5.$ | ||
| + | '''(2)''' Durch Fortsetzung des rekursiven Algorithmuses erhält man für große $\nu$–Werte: $y_\nu = y_{\nu - 12} $ ⇒ $T_0/T_{\rm A}= 12.$ }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 280: | Zeile 174: | ||
[[Datei:Exercises_binomial_fertig.png|right]] | [[Datei:Exercises_binomial_fertig.png|right]] | ||
| − | *Wählen Sie zunächst die Nummer '''1''' ... ''' | + | *Wählen Sie zunächst die Nummer '''1''' ... '''10''' der zu bearbeitenden Aufgabe. |
*Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. | *Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. | ||
*Lösung nach Drücken von „Musterlösung”. | *Lösung nach Drücken von „Musterlösung”. | ||
*Die Nummer '''0''' entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart. | *Die Nummer '''0''' entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart. | ||
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | '''(1)''' Die Filterkoeffizienten seien $a_0=0.25$, $a_1=0.5$, $a_2=0.25$, $b_1=b_2=0$. Um welches Filter handelt es sich? <br> Interpretieren Sie die Impulsantwort $〈h_ν〉$, die Sprungantwort $〈\sigma_ν〉$ und die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$ jeweils in zeitdiskreter Darstellung.}} | ||
| − | + | :* Aufgrund der fehlenden $b$–Koeffizienten handelt es sich um ein nichtrekursives digitales Filter ⇒ FIR–Filter (Finite Impulse Response). | |
| − | * | + | :* Die Impulsantwort setzt sich aus $M+1=3$ Diraclinien zusammen: $〈h_ν〉= 〈a_0, \ a_1,\ a_2〉= 〈0.25, \ 0.5,\ 0.25,\ 0, \ 0, \ 0,\text{...}〉 $. |
| − | * | + | :* Die Sprungantwort lautet: $〈\sigma_ν〉= 〈0.25, \ 0.75,\ 1,\ 1, \ 1, \ 1,\text{...}〉 $. Der Endwert ergibt sich zu $H(f=0)=a_0+a_1+a_2 = 1$. |
| + | :* Die Verzerrungen erkennt man auch aus der Rechteckantwort $〈\rho_ν^{(2, 8)}〉= 〈0,\ 0, 0.25, \ 0.75,\ 1,\ 1, \ 1, \ 1, \ 1, \ 0.75, \ 0.25, \ \text{...}〉$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(2)''' Wie unterscheiden sich die Ergebnisse mit $a_2=-0.25$? }} | ||
| + | :* Mit $H(f=0)= 0.5$ ergeben sich vergleichbare Folgen ⇒ Sprungantwort: $〈\sigma_ν〉= 〈0.25, \ 0.75,\ 0.5,\ 0.5, \ 0.5, \ 0.5,\text{...}〉 $. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(3)''' Nun seien die Filterkoeffizienten $a_0=1$, $b_1=0.9$ sowie $a_1=a_2= b_2=0$. Um welches Filter handelt es sich? Interpretieren Sie $〈h_ν〉$.}} |
| − | + | :* Es handelt sich um ein IIR–Filter (Infinite Impulse Response) erster Ordnung. Es ist das zeitdiskrete Analogon zum RC–Tiefpass. | |
| − | + | :* Mit $h_0= 1$ gilt $h_1= h_0 \cdot b_0= 0.9$, $h_2= h_1 \cdot b_0= b_0^2=0.81$, $h_3= h_2 \cdot b_0= b_0^3=0.729$, usw. ⇒ $〈h_ν〉$ reicht bis ins Unendliche. | |
| − | + | :* $h(t) = {\rm e}^{-t/T}$ mit $T$: Schnittpunkt $($Tangente bei $t=0$, Abszisse$)$ ⇒ $h_\nu= h(\nu \cdot T_{\rm A}) = {\rm e}^{-\nu/(T/T_{\rm A})}$ mit $T/T_{\rm A} = 1/(h_0-h_1)= 10$. | |
| + | :* Unterschiedliche Werte für zeitkontinuierliche und zeitdiskrete Impulsantwort. Für Erstere ergeben sich die Werte $1.0, \ 0.9048,\ 0.8187$ ... | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(4)''' Die Filtereinstellung wird beibehalten. Interpretieren Sie die Sprungantwort $〈h_ν〉$ und die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$. Wie groß ist $H(f=0)$?}} |
| − | + | :* Sprungantwort ist Integral über Impulsantwort: $\sigma(t) = T \cdot (1-{\rm e}^{-t/T})$ ⇒ $\sigma_\nu= 10 \cdot (1-{\rm e}^{-\nu/10})$ ⇒ $\sigma_0=1$, $\sigma_1=1.9$, $\sigma_2=2.71$, ... | |
| − | + | :* Für große $\nu$–Werte tendiert die (zeitdiskrete) Sprungantwort gegen $H(f=0)= 10$: $\sigma_{40}=9.867$, $\sigma_{50}=9.954$, $\sigma_\infty=10$. | |
| − | + | :* Die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$ steigt mit einer Verzögerung von $2$ wie $〈\sigma_ν〉$. Im Bereich $\nu \ge 8$ fallen die $\rho_ν$–Werte exponentiell ab. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Wir betrachten weiterhin das Filter mit $a_0=1$, $b_1=0.9$, $a_1=a_2= b_2=0$. Wie lautet $〈y_ν〉$ für die Eingangsfolge $〈x_ν〉= 〈1,\ 0, -0.5〉$? <br> ''Hinweis'': Die Aufgabe lässt sich ebenfalls mit diesem Programm lösen, obwohl die hier betrachtete Konstellation nicht direkt einstellbar ist.}} |
| − | + | :* Man behilft sich, indem man $a_2=-0.5$ setzt und dafür die Eingangsfolge auf $〈x_ν〉= 〈1,\ 0,\ 0,\ \text{ ...}〉$ ⇒ „Diracfunktion” reduziert. | |
| − | + | :* Die Impulsantwort dieses Filters $($mit $a_2=0)$ wurde in (3) ermittelt: $h_0= 1$, $h_1= 0.9$, $h_2= 0.81$, $h_3= 0.729$, $h_4= 0.646$. | |
| − | + | :* Somit ist das Ergebnis: $y_0 = h_0= 1$, $y_1= h_1= 0.9$, $y_2 =h_2-h_0/2= 0.31$, $y_3 =h_3-h_1/2= 0.279$, $y_4 =h_4-h_2/2= 0.251$. | |
| − | + | :* Vorsicht: Sprungantwort und Rechteckantwort beziehen sich nun auf das fiktive Filter $(a_2=-0.5)$, nicht auf das eigentliche Filter $(a_2=0)$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(6)''' Betrachten und interpretieren Sie die Impulsanwort und die Sprungantwort für die Filterkoeffizienten $a_0=1$, $b_1=1$, $a_1=a_2= b_2=0$. }} |
| − | + | :* Das System ist instabil: Eine zeitdiskrete Diracfunktion am Eingang $($bei $t=0)$ bewirkt am Ausgang unendlich viele Diracs gleicher Höhe. | |
| − | + | :* Die zeitdiskrete Sprungfunktion am Eingang bewirkt am Ausgang unendlich viele Diracs mit monoton steigenden Gewichten (bis ins Unendliche). | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(7)''' Betrachten und interpretieren Sie Impulsanwort und Sprungantwort für die Filterkoeffizienten $a_0=1$, $b_1=-1$, $a_1=a_2= b_2=0$. }} |
| + | :* Nun sind die Gewichte der Impulsantwort $〈h_ν〉$ nicht konstant gleich $1$, sondern alternierend $\pm 1$. Das System ist ebenfalls instabil. | ||
| + | :* Bei $〈\sigma_ν〉$ wechseln sich dagegen die Gewichte alternierend zwischen $1$ $($bei geradem $\nu)$ und $0$ $($bei ungeradem $\nu)$ ab. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | '''(8)''' Wir betrachten den „Sinusgenerator”: $a_1=0.5$, $b_1=\sqrt{3}= 1.732$, $b_2=-1.$ Vergleichen Sie die Impulsantwort mit den Werten von $\text{Beispiel 4}$. <br> Wie beinflussen die Parameter $a_1$ und $b_1$ die Periodendauer $T_0/T_{\rm A}$ und die Amplitude $A$ der Sinusfunktion? }} | |
| + | :* $〈x_ν〉=〈1, 0, 0, \text{...}〉$ ⇒ $〈y_ν〉=〈0, 0.5, 0.866, 1, 0.866, 0.5, 0, -0.5, -0.866, -1, -0.866, -0.5, 0, \text{...}〉$ ⇒ Sinus, $T_0/T_{\rm A}= 12$, $A = 1$. | ||
| + | :* Die Vergrößerung/Verkleinerung von $b_1$ führt zu größerer/kleinerem $T_0/T_{\rm A}$ und zu größerem/kleinerem $A$. Es muss $b_1 < 2$ gelten. | ||
| + | :* $a_1$ beinflusst nur die Amplitude, nicht die Periode. Für $a_1$ gibt es keine Wertebegrenzumg. Negatives $a_1$ führt zur Minus–Sinusfunktion. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Die Grundeinstellung bleibt erhalten. Mit welchen $a_1$ und $b_1$ ergibt sich eine Sinusfunktion mit Periodendauer $T_0/T_{\rm A}=16$ und Amplitude $A=1$? }} |
| + | :* Durch Probieren erreicht man mit $b_1= 1.8478$ genau die Periode $T_0/T_{\rm A}=16.$ Dadurch erhöht sich die Amplitude auf $A=1.307$. | ||
| + | :* Die Anpassung des Parameters $a_1= 0.5/1.307=0.3826$ führt dann zur gewünschten Amplitude $A=1$. | ||
| + | :* Oder man kann das auch wie im Beispiel berechnen: $b_1 = 2 \cdot \cos ( {2{\rm{\pi }}\cdot{T_{\rm A}}/{T_0 }})= 2 \cdot \cos (\pi/8)=1.8478$, $a_1 = \sin (\pi/8)=0.3827$. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | '''(10)''' Wir gehen weiter vom „Sinusgenerator” $(9)$ aus. Welche Modifikationen muss man vornehmen, um damit einen „Cosinus” zu generieren?}} | |
| − | + | :* Mit $a_1=0.3826$, $b_1=\sqrt{3}= 1.8478$, $b_2=-1$ sowie $〈x_ν〉=〈1, 1, 1, \text{...}〉$ ist die Folge $〈y_ν〉$ das zeitdiskrete Analogon der Sprungantwort $\sigma(t)$. | |
| + | :* Die Sprungantwort ist das Integral über $\sin(\pi \cdot \tau/8)$ in den Grenzen von $\tau = 0$ bis $\tau = t$ ⇒ $\sigma(t) = - 8/\pi \cdot \cos(\pi \cdot \tau/8)+1$. | ||
| + | :* Verändert man $a_1=0.3826$ auf $a_1=-0.3826 \cdot \pi/8 = 0.1502$, dann ist $\sigma(t) = \cos(\pi \cdot \tau/8)-1$ ⇒ Werte zwischen $0$ und $-2$. | ||
| + | :* Würde man im Blockschaltbild noch $z_\nu = y_\nu + 1$ hinzufügen, so hätte $z_\nu$ einen zeitdiskreten Cosinusverlauf mit $T_0/T_{\rm A}=16$ und $A=1$. | ||
| + | |||
| + | |||
| + | [[Datei:Exercise_impuls_v2.png|right |frame| Bildschirmabzug der englischen Version '''Korrektur''' noch ändern, auch D]] | ||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(A)''' Auswahl des Eingangssignals $($Dirac, Sprung oder Rechteck$)$ |
| − | '''( | + | '''(B)''' Einstellungen für Abszisse, Ordinate und Geschwindigkeit |
| − | '''( | + | '''(C)''' Bedienfeld $($Start, Einzelschritt, Gesamt, Pause, Reset$)$ |
| − | '''( | + | '''(D)''' Blockschaltbild mit schrittweiser Anpassung aller Werte |
| − | '''( | + | '''(E)''' Grafikfeld für Ausgabe der Ausgangsfolge |
| − | '''( | + | '''(F)''' Aufgabenauswahl |
| − | + | '''(G)''' Fragen und Lösungen | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | ||
| − | |||
| − | |||
<br clear=all> | <br clear=all> | ||
| − | |||
| − | |||
| − | |||
==Über die Autoren== | ==Über die Autoren== | ||
| + | <br> | ||
Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
*Die erste Version wurde 2005 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Bettina_Hirner_.28Diplomarbeit_LB_2005.29|Bettina Hirner]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). | *Die erste Version wurde 2005 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Bettina_Hirner_.28Diplomarbeit_LB_2005.29|Bettina Hirner]] im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). | ||
| − | *2020 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende# | + | *2020 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Andr.C3.A9_Schulz_.28Bachelorarbeit_LB_2020.29|André Schulz]] (Bachelorarbeit LB, Betreuer: [[Biografien_und_Bibliografien/Beteiligte_der_Professur_Leitungsgebundene_Übertragungstechnik#Benedikt_Leible.2C_M.Sc._.28bei_L.C3.9CT_seit_2017.29|Benedikt Leible]] und [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|Tasnád Kernetzky]] ) unter „HTML5” neu gestaltet. |
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{ | + | {{LntAppletLinkDeEn|digitalFilters|digitalFilters_en}} |
Aktuelle Version vom 26. Oktober 2023, 11:45 Uhr
Applet in neuem Tab öffnen Open English Version
Inhaltsverzeichnis
Programmbeschreibung
Das Applet soll die Eigenschaften digitaler Filter verdeutlichen, wobei wir uns auf Filter der Ordnung $M=2$ beschränken. Behandelt werden sowohl nichtrekursive Filter $\rm (FIR$, Finite Impulse Response$)$ als auch rekursive Filter $\rm (IIR$, Infinite Impulse Response$)$.
Das Eingangssignal $x(t)$ wird durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht. Berechnet wird die Ausgangsfolge $〈y_ν〉$, also die zeitdiskrete Darstellung des Ausgangssignal $y(t)$.
- $T_{\rm A}$ bezeichnet den zeitlichen Abstand zwischen zwei Abtastwerten.
- Zudem beschränken uns auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ sowie $y_ν \equiv 0$ für $ν < 0$.
Weiter ist anzumerken: Wir bezeichnen die Ausgangsfolge $〈y_ν〉$ als
(1) die zeitdiskrete Impulsantwort $〈h_ν〉$, wenn am Eingang die „zeitdiskrete Diracfunktion” anliegt: $〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉,$
(2) die zeitdiskrete Sprungantwort $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt: $〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 ,$
(3) die zeitdiskrete Rechteckantwort $〈\rho_ν^{(2, 4)}〉$, wenn am Eingang die „zeitdiskrete Rechteckfunktion” anliegt: $〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 ;$
In Hochkommata angegeben sind hier der Beginn der Einsen $(\nu =2)$ und die Stelle der letzten Eins $(\nu =4)$.
Theoretischer Hintergrund
Allgemeines Blockschaltbild
Jedes Signal $x(t)$ kann an einem Rechner nur durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt werden, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht.
- Der zeitliche Abstand $T_{\rm A}$ zwischen zwei Abtastwerten ist dabei durch das Abtasttheorem nach oben begrenzt.
- Wir beschränken uns hier auf kausale Signale und Systeme, das heißt, es gilt $x_ν \equiv 0$ für $ν < 0$.
- Um den Einfluss eines linearen Filters mit Frequenzgang $H(f)$ auf das zeitdiskrete Eingangssignal $〈x_ν〉$ zu erfassen, bietet es sich an, auch das Filter zeitdiskret zu beschreiben. Im Zeitbereich geschieht das mit der zeitdiskreten Impulsantwort $〈h_ν〉$.
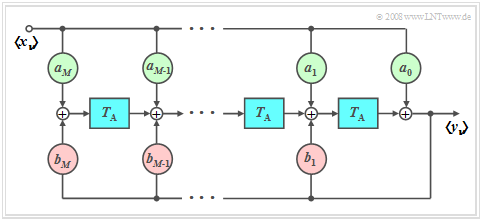
- Rechts sehen Sie das entsprechende Blockschaltbild. Für die Abtastwerte des Ausgangssignals $〈y_ν〉$ gilt somit:
- $$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu } \cdot x_{\nu - \mu } + \sum\limits_{\mu = 1}^M {b_\mu } \cdot y_{\nu - \mu } .$$
Hierzu ist Folgendes zu bemerken:
- Der Index $\nu$ bezieht sich auf Folgen, zum Beispiel am Eingang $〈x_ν〉$ und Ausgang $〈y_ν〉$.
- Den Index $\mu$ verwenden wir dagegen für die Kennzeichnung der $a$– und $b$–Filterkoeffizienten.
- Die erste Summe beschreibt die Abhängigkeit des aktuellen Ausgangs $y_ν$ vom aktuellen Eingang $x_ν$ und von den $M$ vorherigen Eingangswerten $x_{ν-1}$, ... , $x_{ν-M}.$
- Die zweite Summe kennzeichnet die Beeinflussung von $y_ν$ durch die vorherigen Werte $y_{ν-1}$, ... , $y_{ν-M}$ am Filterausgang. Sie gibt den rekursiven Teil des Filters an.
- Den ganzzahligen Parameter $M$ bezeichnet man als die Ordnung des digitalen Filters. Im Programm ist dieser Wert auf $M\le 2$ begrenzt.
$\text{Definitionen:}$
(1) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Impulsantwort $〈h_ν〉$, wenn am Eingang die „zeitdiskrete Diracfunktion” anliegt:
- $$〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉 .$$
(2) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Sprungantwort $〈\sigma_ν〉$, wenn am Eingang die „zeitdiskrete Sprungfunktion” anliegt:
- $$〈x_ν〉= 〈1,\ 1,\ 1,\ 1,\ 1,\ 1,\ 1, \text{...}〉 .$$
(3) Man bezeichnet die Ausgangsfolge $〈y_ν〉$ als die zeitdiskrete Rechteckantwort $〈\rho_ν^{(2, 4)}〉$, wenn am Eingang die „zeitdiskrete Rechteckfunktion” anliegt:
- $$〈x_ν〉= 〈0,\ 0,\ 1,\ 1,\ 1,\ 0,\ 0, \text{...}〉 .$$
- In Hochkommata angegeben sind hier der Beginn der Einsen $(\nu =2)$ und die Stelle der letzten Eins $(\nu =4)$.
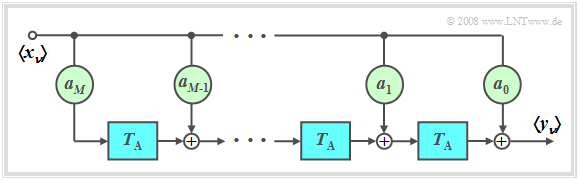
Nichtrekursives Filter ⇒ FIR–Filter
$\text{Definition:}$ Sind alle Rückführungskoeffizienten $b_{\mu} = 0$, so spricht von einem nichtrekursiven Filter. In der englischsprachigen Literatur ist hierfür auch die Bezeichnung FIR Filter (von „Finite Impulse Response”) gebräuchlich.
Für die Ordnung $M$ gilt:
- Der Ausgangswert $y_ν$ hängt nur vom aktuellen und den $M$ vorherigen Eingangswerten ab:
- $$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu \cdot x_{\mu - \nu } } .$$
- Zeitdiskrete Impulsantwort mit $〈x_ν〉= 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉$:
- $$〈h_\nu〉= 〈a_0,\ a_1,\ \text{...} \ ,\ a_M〉 .$$
- Aufgrund unserer Nomenklatur kann man die zeitdiskrete Impulsantwort auch mit $〈h_\mu〉= 〈a_0,\ a_1,\ \text{...} \ ,\ a_M〉 $ bezeichnen.
$\text{Beispiel 1:}$ Ein Zweiwegekanal, bei dem
- das Signal auf dem Hauptpfad gegenüber dem Eingangssignal ungedämpft, aber um $2\ \rm µ s$ verzögert ankommt, und
- in $4\ \rm µ s$ Abstand – also absolut zur Zeit $t = 6\ \rm µ s$ – ein Echo mit halber Amplitude nachfolgt,
kann durch ein nichtrekursives Filter entsprechend obiger Skizze nachgebildet werden, wobei folgende Parameterwerte einzustellen sind:
- $$M = 3,\quad T_{\rm A} = 2\;{\rm{µ s} },\quad a_{\rm 0} = 0,\quad a_{\rm 1} = 1, \quad a_{\rm 2} = 0, \quad a_{\rm 3} = 0.5.$$
$\text{Beispiel 2:}$ Betrachtet wird ein nichtrekursives Filter mit den Filterkoeffizienten $a_0 = 1,\hspace{0.15cm} a_1 = 2,\hspace{0.15cm} a_2 = 1.$
(1) Die herkömmliche Impulsantwort lautet: $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$
⇒ Zeitdiskrete Impulsantwort: $〈h_\mu〉= 〈1,\ 2,\ 1〉$.
(2) Der Frequenzgang $H(f)$ ist die Fouriertransformierte von $h(t)$. Nach Anwendung des Verschiebungssatzes:
- $$H(f) = 2 \cdot \big [ {1 + \cos ( {2{\rm{\pi }\cdot }f \cdot T_{\rm A} } )} \big ] \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm A} }\hspace{0.5cm}\Rightarrow \hspace{0.5cm}H(f = 0) = 4.$$
(3) Daraus folgt: Die zeitdiskrete Sprungantwort $〈\sigma_ν〉$ tendiert für große $\nu$ gegen $4$.
(4) Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;0,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt
- $$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;2,\;1,\;0,\;1,\;2,\;1,\;0,\;0,\;0,\;0,\; \text{...} \;} \right\rangle. $$
(5) Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;1,\;0,\;0,\;1,\;0,\;0,\;0,\;\text{...} } \hspace{0.05cm} \right\rangle$ mit $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, \ 2,\ 1 } \hspace{0.05cm}\right\rangle$ ergibt
- $$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;3,\;2,\;2,\;1,\;0,\;0,\;0,\;0,\;0,\; \text{...} \;} \right\rangle. $$
Rekursives Filter ⇒ IIR–Filter
$\text{Definition:}$
- Ist zumindest einer der Rückführungskoeffizienten $b_{\mu} \ne 0$, so spricht von einem rekursiven Filter (siehe rechte Grafik). Insbesondere in der englischsprachigen Literatur ist hierfür auch die Bezeichnung IIR Filter (von „Infinite Impulse Response”) gebräuchlich. Dieser Filtertyp wird in der Verrsuchsdurchführung ausführlich behandelt.
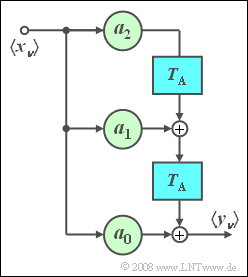
- Sind zusätzlich alle Vorwärtskoeffizienten identisch $a_\mu = 0$ mit Ausnahme von $a_0$, so liegt ein rein rekursives Filter vor (siehe linke Grafik).
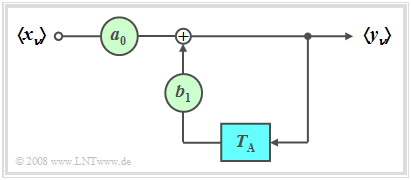
Im Folgenden beschränken wir uns auf den Sonderfall „Rein rekursives Filter erster Ordnung”. Dieses Filter weist folgende Eigenschaften auf:
- Der Ausgangswert $y_ν$ hängt (indirekt) von unendlich vielen Eingangswerten ab:
- $$y_\nu = \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot x_{\nu - \mu } .}$$
- Dies zeigt die folgende Rechung:
- $$y_\nu = a_0 \cdot x_\nu + b_1 \cdot y_{\nu - 1} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + {b_1} ^2 \cdot y_{\nu - 2} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + a_0 \cdot {b_1} ^2 \cdot x_{\nu - 2} + {b_1} ^3 \cdot y_{\nu - 3} = \text{...}. $$
- Die zeitdiskrete Impulsantwort ist definitionsgemäß gleich der Ausgangsfolge, wenn am Eingang eine einzelne „Eins” bei $t =0$ anliegt.
- $$h(t)= \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉= 〈\hspace{0.05cm}a_0, \ a_0\cdot {b_1}, \ a_0\cdot {b_1}^2, \ \text{...} \hspace{0.05cm}〉.$$
$\text{Fazit:}$ Bei einem rekursiven Filter reicht die (zeitdiskrete) Impulsantwort schon mit $M = 1$ bis ins Unendliche:
- Aus Stabilitätsgründen muss $b_1 < 1$ gelten.
- Bei $b_1 = 1$ würde sich die Impulsantwort $(h(t)$ bzw. $〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉)$ bis ins Unendliche erstrecken und bei $b_1 > 1$ würde sie sogar bis ins Unendliche anklingen.
- Bei einem solchen rekursiven Filter erster Ordnung ist jede einzelne Diraclinie genau um den Faktor $b_1$ kleiner als die vorherige Diraclinie:
- $$h_{\mu} = h(\mu \cdot T_{\rm A}) = {b_1} \cdot h_{\mu -1}.$$
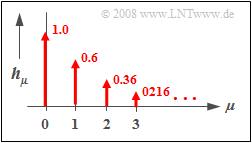
$\text{Beispiel 3:}$ Die nebenstehende Grafik zeigt die zeitdiskrete Impulsantwort $〈\hspace{0.05cm}h_\mu\hspace{0.05cm}〉$ eines rekursiven Filters erster Ordnung mit den Parametern $a_0 = 1$ und $b_1 = 0.6$.
- Der (zeitdiskrete) Verlauf ist exponentiell abfallend und erstreckt sich bis ins Unendliche.
- Das Verhältnis der Gewichte zweier aufeinanderfolgender Diracs ist jeweils $b_1 = 0.6$.
Rekursives Filter als Sinus–Generator
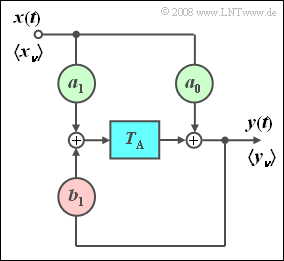
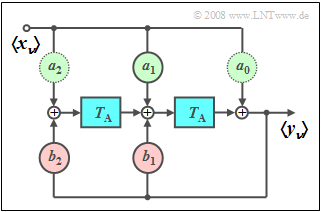
Die Grafik zeigt ein digitales Filter zweiter Ordnung, das zur Erzeugung einer zeitdiskreten Sinusfunktion auf einem digitalen Signalprozessor $\rm (DSP)$ geeignet ist, wenn die Eingangsfolge $\left\langle \hspace{0.05cm} {x_\nu } \hspace{0.05cm}\right\rangle = = 〈1,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0, \text{...}〉$ eine (zeitdiskrete) Diracfunktion ist:
- $$\left\langle \hspace{0.05cm}{y_\nu }\hspace{0.05cm} \right\rangle = \left\langle {\, \sin ( {\nu \cdot T_{\rm A} \cdot \omega _0 } )\, }\right\rangle .$$
Die fünf Filterkoeffizienten ergeben sich aus der $Z$-Transformation:
- $$Z \big \{ {\sin ( {\nu T{\rm A}\cdot \omega _0 } )} \big \} = \frac{{z \cdot \sin \left( {\omega _0 \cdot T_{\rm A}} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 \cdot T_{\rm A}} \right) + 1}}.$$
Nach Umsetzung dieser Gleichung durch ein rekursives Filter zweiter Ordnung erhält man folgende Filterkoeffizienten:
- $$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 \cdot T_{\rm A}} \right),\quad a_2 = 0, \quad b_1 = 2 \cdot \cos \left( {\omega _0 \cdot T_{\rm A}} \right),\quad b_2 = - 1.$$
- Auf die Filterkoeffizienten $a_0$ und $a_2$ kann verzichtet werden und $b_2=-1$ hat einen festen Wert.
- Die Kreisfrequenz $\omega_0$ der Sinusschwingung wird also nur durch $a_1$ und $b_1$ festelegt.
$\text{Beispiel 4:}$ Es gelte $a_1 = 0.5$, $b_1 = \sqrt 3$, $x_0 = 1$ und $x_{\nu \hspace{0.05cm}\ne\hspace{0.05cm} 0} = 0$.
(1) Dann gilt für die Ausgangswerte $y_\nu$ zu den Zeitpunkten $\nu \ge 0$:
- $y_0 = 0;$
- $y_1 = 0.5$ ⇒ die „$1$” am Eingang wirkt sich wegen $a_0= 0$ am Ausgang erst zum Zeitpunkt $\nu = 1$ aus;
- $y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \approx 0.866$ ⇒ bei $\nu = 2$ wird auch der rekursive Teil des Filters wirksam;
- $y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1$ ⇒ für $\nu \ge 2$ ist das Filter rein rekursiv: $y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2}$;
- $y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$
- $y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = 0.5;$
- $y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$
- $y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} = - 0.5.$
(2) Durch Fortsetzung des rekursiven Algorithmuses erhält man für große $\nu$–Werte: $y_\nu = y_{\nu - 12} $ ⇒ $T_0/T_{\rm A}= 12.$
Versuchsdurchführung
- Wählen Sie zunächst die Nummer 1 ... 10 der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
(1) Die Filterkoeffizienten seien $a_0=0.25$, $a_1=0.5$, $a_2=0.25$, $b_1=b_2=0$. Um welches Filter handelt es sich?
Interpretieren Sie die Impulsantwort $〈h_ν〉$, die Sprungantwort $〈\sigma_ν〉$ und die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$ jeweils in zeitdiskreter Darstellung.
- Aufgrund der fehlenden $b$–Koeffizienten handelt es sich um ein nichtrekursives digitales Filter ⇒ FIR–Filter (Finite Impulse Response).
- Die Impulsantwort setzt sich aus $M+1=3$ Diraclinien zusammen: $〈h_ν〉= 〈a_0, \ a_1,\ a_2〉= 〈0.25, \ 0.5,\ 0.25,\ 0, \ 0, \ 0,\text{...}〉 $.
- Die Sprungantwort lautet: $〈\sigma_ν〉= 〈0.25, \ 0.75,\ 1,\ 1, \ 1, \ 1,\text{...}〉 $. Der Endwert ergibt sich zu $H(f=0)=a_0+a_1+a_2 = 1$.
- Die Verzerrungen erkennt man auch aus der Rechteckantwort $〈\rho_ν^{(2, 8)}〉= 〈0,\ 0, 0.25, \ 0.75,\ 1,\ 1, \ 1, \ 1, \ 1, \ 0.75, \ 0.25, \ \text{...}〉$.
(2) Wie unterscheiden sich die Ergebnisse mit $a_2=-0.25$?
- Mit $H(f=0)= 0.5$ ergeben sich vergleichbare Folgen ⇒ Sprungantwort: $〈\sigma_ν〉= 〈0.25, \ 0.75,\ 0.5,\ 0.5, \ 0.5, \ 0.5,\text{...}〉 $.
(3) Nun seien die Filterkoeffizienten $a_0=1$, $b_1=0.9$ sowie $a_1=a_2= b_2=0$. Um welches Filter handelt es sich? Interpretieren Sie $〈h_ν〉$.
- Es handelt sich um ein IIR–Filter (Infinite Impulse Response) erster Ordnung. Es ist das zeitdiskrete Analogon zum RC–Tiefpass.
- Mit $h_0= 1$ gilt $h_1= h_0 \cdot b_0= 0.9$, $h_2= h_1 \cdot b_0= b_0^2=0.81$, $h_3= h_2 \cdot b_0= b_0^3=0.729$, usw. ⇒ $〈h_ν〉$ reicht bis ins Unendliche.
- $h(t) = {\rm e}^{-t/T}$ mit $T$: Schnittpunkt $($Tangente bei $t=0$, Abszisse$)$ ⇒ $h_\nu= h(\nu \cdot T_{\rm A}) = {\rm e}^{-\nu/(T/T_{\rm A})}$ mit $T/T_{\rm A} = 1/(h_0-h_1)= 10$.
- Unterschiedliche Werte für zeitkontinuierliche und zeitdiskrete Impulsantwort. Für Erstere ergeben sich die Werte $1.0, \ 0.9048,\ 0.8187$ ...
(4) Die Filtereinstellung wird beibehalten. Interpretieren Sie die Sprungantwort $〈h_ν〉$ und die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$. Wie groß ist $H(f=0)$?
- Sprungantwort ist Integral über Impulsantwort: $\sigma(t) = T \cdot (1-{\rm e}^{-t/T})$ ⇒ $\sigma_\nu= 10 \cdot (1-{\rm e}^{-\nu/10})$ ⇒ $\sigma_0=1$, $\sigma_1=1.9$, $\sigma_2=2.71$, ...
- Für große $\nu$–Werte tendiert die (zeitdiskrete) Sprungantwort gegen $H(f=0)= 10$: $\sigma_{40}=9.867$, $\sigma_{50}=9.954$, $\sigma_\infty=10$.
- Die Rechteckantwort $〈\rho_ν^{(2, 8)}〉$ steigt mit einer Verzögerung von $2$ wie $〈\sigma_ν〉$. Im Bereich $\nu \ge 8$ fallen die $\rho_ν$–Werte exponentiell ab.
(5) Wir betrachten weiterhin das Filter mit $a_0=1$, $b_1=0.9$, $a_1=a_2= b_2=0$. Wie lautet $〈y_ν〉$ für die Eingangsfolge $〈x_ν〉= 〈1,\ 0, -0.5〉$?
Hinweis: Die Aufgabe lässt sich ebenfalls mit diesem Programm lösen, obwohl die hier betrachtete Konstellation nicht direkt einstellbar ist.
- Man behilft sich, indem man $a_2=-0.5$ setzt und dafür die Eingangsfolge auf $〈x_ν〉= 〈1,\ 0,\ 0,\ \text{ ...}〉$ ⇒ „Diracfunktion” reduziert.
- Die Impulsantwort dieses Filters $($mit $a_2=0)$ wurde in (3) ermittelt: $h_0= 1$, $h_1= 0.9$, $h_2= 0.81$, $h_3= 0.729$, $h_4= 0.646$.
- Somit ist das Ergebnis: $y_0 = h_0= 1$, $y_1= h_1= 0.9$, $y_2 =h_2-h_0/2= 0.31$, $y_3 =h_3-h_1/2= 0.279$, $y_4 =h_4-h_2/2= 0.251$.
- Vorsicht: Sprungantwort und Rechteckantwort beziehen sich nun auf das fiktive Filter $(a_2=-0.5)$, nicht auf das eigentliche Filter $(a_2=0)$.
(6) Betrachten und interpretieren Sie die Impulsanwort und die Sprungantwort für die Filterkoeffizienten $a_0=1$, $b_1=1$, $a_1=a_2= b_2=0$.
- Das System ist instabil: Eine zeitdiskrete Diracfunktion am Eingang $($bei $t=0)$ bewirkt am Ausgang unendlich viele Diracs gleicher Höhe.
- Die zeitdiskrete Sprungfunktion am Eingang bewirkt am Ausgang unendlich viele Diracs mit monoton steigenden Gewichten (bis ins Unendliche).
(7) Betrachten und interpretieren Sie Impulsanwort und Sprungantwort für die Filterkoeffizienten $a_0=1$, $b_1=-1$, $a_1=a_2= b_2=0$.
- Nun sind die Gewichte der Impulsantwort $〈h_ν〉$ nicht konstant gleich $1$, sondern alternierend $\pm 1$. Das System ist ebenfalls instabil.
- Bei $〈\sigma_ν〉$ wechseln sich dagegen die Gewichte alternierend zwischen $1$ $($bei geradem $\nu)$ und $0$ $($bei ungeradem $\nu)$ ab.
(8) Wir betrachten den „Sinusgenerator”: $a_1=0.5$, $b_1=\sqrt{3}= 1.732$, $b_2=-1.$ Vergleichen Sie die Impulsantwort mit den Werten von $\text{Beispiel 4}$.
Wie beinflussen die Parameter $a_1$ und $b_1$ die Periodendauer $T_0/T_{\rm A}$ und die Amplitude $A$ der Sinusfunktion?
- $〈x_ν〉=〈1, 0, 0, \text{...}〉$ ⇒ $〈y_ν〉=〈0, 0.5, 0.866, 1, 0.866, 0.5, 0, -0.5, -0.866, -1, -0.866, -0.5, 0, \text{...}〉$ ⇒ Sinus, $T_0/T_{\rm A}= 12$, $A = 1$.
- Die Vergrößerung/Verkleinerung von $b_1$ führt zu größerer/kleinerem $T_0/T_{\rm A}$ und zu größerem/kleinerem $A$. Es muss $b_1 < 2$ gelten.
- $a_1$ beinflusst nur die Amplitude, nicht die Periode. Für $a_1$ gibt es keine Wertebegrenzumg. Negatives $a_1$ führt zur Minus–Sinusfunktion.
(9) Die Grundeinstellung bleibt erhalten. Mit welchen $a_1$ und $b_1$ ergibt sich eine Sinusfunktion mit Periodendauer $T_0/T_{\rm A}=16$ und Amplitude $A=1$?
- Durch Probieren erreicht man mit $b_1= 1.8478$ genau die Periode $T_0/T_{\rm A}=16.$ Dadurch erhöht sich die Amplitude auf $A=1.307$.
- Die Anpassung des Parameters $a_1= 0.5/1.307=0.3826$ führt dann zur gewünschten Amplitude $A=1$.
- Oder man kann das auch wie im Beispiel berechnen: $b_1 = 2 \cdot \cos ( {2{\rm{\pi }}\cdot{T_{\rm A}}/{T_0 }})= 2 \cdot \cos (\pi/8)=1.8478$, $a_1 = \sin (\pi/8)=0.3827$.
(10) Wir gehen weiter vom „Sinusgenerator” $(9)$ aus. Welche Modifikationen muss man vornehmen, um damit einen „Cosinus” zu generieren?
- Mit $a_1=0.3826$, $b_1=\sqrt{3}= 1.8478$, $b_2=-1$ sowie $〈x_ν〉=〈1, 1, 1, \text{...}〉$ ist die Folge $〈y_ν〉$ das zeitdiskrete Analogon der Sprungantwort $\sigma(t)$.
- Die Sprungantwort ist das Integral über $\sin(\pi \cdot \tau/8)$ in den Grenzen von $\tau = 0$ bis $\tau = t$ ⇒ $\sigma(t) = - 8/\pi \cdot \cos(\pi \cdot \tau/8)+1$.
- Verändert man $a_1=0.3826$ auf $a_1=-0.3826 \cdot \pi/8 = 0.1502$, dann ist $\sigma(t) = \cos(\pi \cdot \tau/8)-1$ ⇒ Werte zwischen $0$ und $-2$.
- Würde man im Blockschaltbild noch $z_\nu = y_\nu + 1$ hinzufügen, so hätte $z_\nu$ einen zeitdiskreten Cosinusverlauf mit $T_0/T_{\rm A}=16$ und $A=1$.
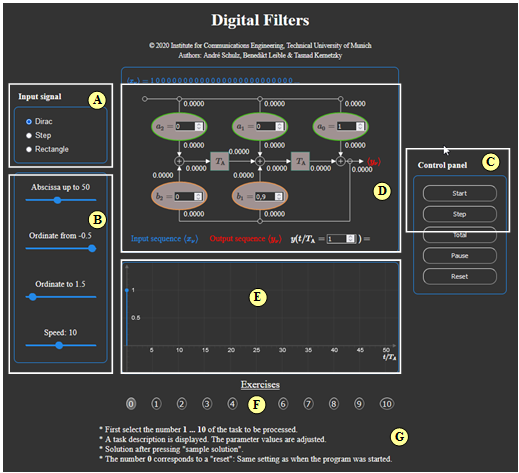
Zur Handhabung des Applets
(A) Auswahl des Eingangssignals $($Dirac, Sprung oder Rechteck$)$
(B) Einstellungen für Abszisse, Ordinate und Geschwindigkeit
(C) Bedienfeld $($Start, Einzelschritt, Gesamt, Pause, Reset$)$
(D) Blockschaltbild mit schrittweiser Anpassung aller Werte
(E) Grafikfeld für Ausgabe der Ausgangsfolge
(F) Aufgabenauswahl
(G) Fragen und Lösungen
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von André Schulz (Bachelorarbeit LB, Betreuer: Benedikt Leible und Tasnád Kernetzky ) unter „HTML5” neu gestaltet.