Zur Verdeutlichung des Matched-Filters

Inhaltsverzeichnis

1 Programmbeschreibung
2 Theoretischer Hintergrund
- 2.1 Detailbeschreibung des zugrunde liegenden Modells
- 2.2 Matched-Filter-Optimierung
3 Interpretation des Matched-Filters
4 Versuchsdurchführung
5 Zur Handhabung des Applets
6 Über die Autoren
7 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Programmbeschreibung

Das Applet soll die Eigenschaften des so genannten „Matched-Filters” $({\rm MF})$ verdeutlichen. Dieses dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude und/oder der Lage einer bekannten Signalform in einer stark verrauschten Umgebung. Oder allgemeiner gesprochen: Das Matched-Filter – manchmal auch als „Optimalfilter” oder als „Korrelationsfilter” bezeichnet – dient dem Nachweis der Signalexistenz.

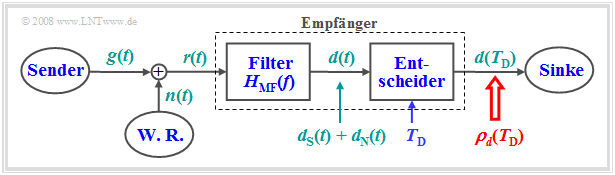
Blockschaltbild des Matched-Filter-Empfängers

Die Grafik zeigt den so genannten Matched-Filter-Empfänger:

Dieser kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem Signal–zu–Rausch–Verhältnis $($englisch: signal–to–noise–ratio, $\rm SNR)$ – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht.
Eine Anwendung ist die Radartechnik, bei der man zwar die Impulsform $g(t)$ kennt, nicht aber, wann der Impuls gesendet wurde und mit welcher Stärke und Verzögerung dieser ankommt.
Das Matched-Filter wird aber auch als Empfangsfilter in digitalen Übertragungssystemen (oder zumindest als Teil davon) eingesetzt, um die Fehlerwahrscheinlichkeit des Systems zu minimieren.

XXX Es fehlt noch: Impulse, Filter, alle ausgegebenen Größen YYY

Theoretischer Hintergrund

Detailbeschreibung des zugrunde liegenden Modells

Für die einzelnen Komponenten des obigen Blockschaltbild gelten folgende Voraussetzungen:

Der Nutzanteil $g(t)$ des Empfangssignals $r(t)=g(t)+n(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $ [g(t) ]^2$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
Das Filterausgangssignal $d(t)= d_{\rm S}(t) + d_{\rm N}(t)$ besteht additiv aus zwei Anteilen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S\hspace{0.04cm}$ignal $g(t)$ zurück, $d_{\rm N}(t)$ auf das $\rm N\hspace{0.04cm}$oise $n(t)$.
Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma_d^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$

Hierbei bezeichnen ${σ_d}^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) Detektionszeitpunkt.

Matched-Filter-Optimierung

Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit Impulsantwort $h(t)$ und Frequenzgang $H(f) =\mathcal{ F}\{h(t)\}$ geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm S$ für „Signal”):

$$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$

Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$:

$$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$

Damit lautet das hier vorliegende Optimierungsproblem:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$

Dieser Quotient wird für den folgenden Frequenzgang $H(f)$ am größten wird:

$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$

Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$:

$$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } } \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \rho _{\rm MF}.$$

$E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:

$$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$

$\text{Herleitung des Matched–Filter–Kriteriums:}$

$(1)$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$:

$$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$

$(2)$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$

$(3)$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ ergibt sich somit die folgende Schranke:

$$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$

$(4)$ Wir setzen für den Filterfrequenzgang nun versuchsweise ein:

$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$

$(5)$ Dann erhält man aus der obigen Gleichung $(2)$ folgendes Ergebnis:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$

$\text{Das heißt:}$

Mit dem Ansatz $(4)$ für das Matched–Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht.
Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen.
Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.

q.e.d.

$\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit Amplitude $\rm 1\hspace{0.05cm}V$, Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden.

Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.

Das beste Ergebnis ⇒ das maximale S/N–Verhältnis erzielt man mit dem Matched-Filter:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$

Das oben angegebene Matched–Filter–Kriterium wird nun schrittweise hergeleitet. Wenn Sie daran nicht interessiert sind, so springen Sie bitte zur Fortsetzungsseite Interpretation des Matched–Filters.

Interpretation des Matched-Filters

Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet:

$$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$

Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort:

$$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$

Diese beiden Funktionen lassen sich wie folgt interpretieren:

Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig.
Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)\equiv 0$ $($„Kausalität”, siehe Buch Lineare zeitinvariante Systeme$)$.
Der Nutzanteil $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der Energie-AKF $\varphi^{^{\bullet} }_{g} (t )$ und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt:

$$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$

$\text{Bitte beachten Sie:}$ Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben:

$$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$

Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich

$$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$

wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.

$\text{Beispiel 2:}$ Wir gehen davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.08cm}ms$ und $\rm 2.5\hspace{0.08cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ gewünscht wird.

Unter diesen Voraussetzungen gilt:

Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ bis $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$ konstant sein.
Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier $\rm si$–förmig.
Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.

Versuchsdurchführung

Überarbeiten

Wählen Sie zunächst die Nummer (1, ... , 10) der zu bearbeitenden Aufgabe.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen. Auch die ausgegebenen Leistungen sind normierte Größen.

Alles normiert

Für (1) soll voreingestellt sein, ohne dass es in der Aufgabenstellung erwähnt wird: Spalt-TP, $A_h=0.5,\ \Delta t_h=1.6,\ \tau_h=0.8, \ T_D = 2$

(1) Der Eingangsimpuls sei gaußförmig mit $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Welche Einstellung führt zum „Matched–Filter”? Wie groß ist $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$?

Das Matched–Filter muss ebenfalls einen gaußförmigen Verlauf haben und es muss gelten: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$.
Das (momentane) Signal–zu–Rauschleistungsverhältnis am Filterausgang ist $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB.
Mit keinem anderen Filter als dem Matched–Filter ist dieses $\rm SNR$ (oder ein noch besseres) zu erreichen.

(2) Das Matched–Filter bei rechteckförmigen Eingangsimpuls mit $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ ist ein Spalt–Tiefpass ⇒ rechteckförmige Impulsantwort.
Wie groß ist hier $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? Interpretieren Sie alle dargestellten Grafiken und die numerischen Ergebnisse auf verschiedene Art und Weise.

Die eingestellten Filterparameter sind $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB.
Die Impulsenergie ist als das Integral über $g(t)^2$ berechenbar ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ ist hier implizit berücksichtigt.
Eine andere Gleichung lautet: $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. Die Rauschvarianz kann z. B. als Integral über $h(t)^2$ berechnet werden: $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$.
Das Nutzsignal $d_{\rm S} (t)= g(t) * h(t)$ hat einen dreieckförmigen Verlauf mit dem Maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$.

(3) Es gelten weiter die Einstellungen von (2) mit Ausnahme von $N_0=0.01 $ ⇒ $N_0=0.02$. Welche Veränderungen sind erkennbar?

Der einzige Unterschied ist die doppelt so große Rauschvarianz $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.

(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $T_{\rm D, \ opt} = 0 $ ⇒ $T_{\rm D} = 0.1$. Wie wirkt sich dieser nichtoptimale Detektionszeitpunkt aus?

Nun ist der Nutzabtastwert $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ kleiner ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. Es ergibt sich eine Verschlechterung um knapp ein dB.
Für die weiteren Aufgaben wird vom optimalen Detektionszeitpunkt $T_{\rm D, \ opt}$ ausgegangen, wenn nicht explizit etwas anderes angegeben wird.

(5) Es gelten wieder die Einstellungen von (3) mit Ausnahme einer niedrigeren Impulsantwort $A_h = 1 $ ⇒ $A_h = 0.8$. Interpretieren Sie die Veränderungen.

Es handelt sich auch mit $A_h \ne = A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber (3) jeweils um den Faktor $0.8^2$ vermindert wird.

(6) Gegenüber (5) wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$?

Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} =21.94$ dB.
Der Gewinn von $21.94$ dB gegenüber (5) lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist.

(7) Wir gehen weiter von der Rechteck–Rechteck–Komination aus mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.2,\ T_{\rm D}=0$.
Interpretieren Sie die Ergebnisse nach Variation der äquivalenten Impulsdauer $\Delta t_h$ von $h(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_h$.

Das Optimum ergibt sich erwartungsgemäß für die äquivalente Impulsdauer $\Delta t_h=\Delta t_g=1$. Dann ist $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$.
Ist $\Delta t_h<\Delta t_g=1$, so ist das Nutzsignal trapezförmig. Für $\Delta t_h=0.6$: $d_{\rm S}^2 (T_{\rm D}=0)= 0.36$ und $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =17.8$ dB.
Auch für $\Delta t_h>1$ ist das Nutzsignal trapezförmig, aber trotzdem $d_{\rm S}^2 (T_{\rm D}=0)= 1$. Die Rauschvarianz $\sigma_d^2$ nimmt kontinuierlich mit $\Delta t_h$ zu.
Für $\Delta t_h=1.4$ ist $\sigma_d^2=0.118$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =18.5$ dB. Gegenüber dem Matched–Filter $(\Delta t_h=1)$ beträgt die Verschlechterung $1.5$ dB.

(8) Interpretieren Sie nun die Ergebnisse für verschiedene $\Delta t_g$ des Eingangsimpulses $g(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_g$.

Die Grafikdarstellung geschieht nach folgender Aufspaltung: $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ (blau) $=20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (violett) Minus $10\cdot \lg \ \big [K \cdot \sigma_d^2 \big ]$ (grün).
Beim betrachteten Parametersatz und $K=10$ ist der grüne Term $10\cdot \lg \ \big [K \cdot \sigma_d^2 \big ] = 0$ dB für alle $\Delta t_g$ ⇒ die blaue und die violette Kurve sind identisch.
Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ steigt von $15.6$ dB $($für $\Delta t_g = 0.6)$ bis $20$ dB $($für $\Delta t_g = 1)$ kontinuierlich an und bleibt für $\Delta t_g > 1$ dann konstant.
Die Einstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ ergibt aber kein Matched-Filter. Vielmehr gilt mit $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB.

Zur Handhabung des Applets

(A) Auswahl eines von vier Quellensignalen

(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)

(C) Ausgabe der verwendeten Programmparameter

(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$

(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$

(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$

(G) Darstellungsauswahl für Zeitbereich

(H) Grafikbereich für Zeitbereich

( I ) Darstellungsauswahl für Frequenzbereich

(J) Grafikbereich für Frequenzbereich

(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2006 von Markus Elsberger im Rahmen seiner Diplomarbeit (LB) mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen