Zur Verdeutlichung des Matched-Filters
Inhaltsverzeichnis
Programmbeschreibung
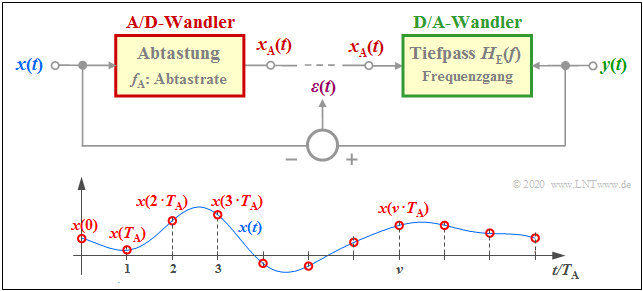
Das Applet behandelt die Systemkomponenten „Abtastung” und „Signalrekonstruktion”, zwei Komponenten, die zum Beispiel für das Verständnis der Pulscodemodulation $({\rm PCM})$ von großer Wichtigkeit sind. Die obere Grafik zeigt das für dieses Applet zugrundeliegende Modell. Darunter gezeichnet sind die Abtastwerte $x(\nu \cdot T_{\rm A})$ des zeitkontinuierlichen Signals $x(t)$. Die (unendliche) Summe über alle diese Abtastwerte bezeichnen wir als das abgetastete Signal $x_{\rm A}(t)$.
- Beim Sender wird aus dem zeitkontinuierlichen Quellensignal $x(t)$ das zeitdiskrete (abgetastete) Signal $x_{\rm A}(t)$ gewonnen. Man nennt diesen Vorgang Abtastung oder A/D–Wandlung.
- Der entsprechende Programmparameter für den Sender ist die Abtastrate $f_{\rm A}= 1/T_{\rm A}$. In der unteren Grafik ist der Abtastabstand $T_{\rm A}$ eingezeichnet.
- Beim Empfänger wird aus dem zeitdiskreten Empfangssignal $y_{\rm A}(t)$ das zeitkontinuierliche Sinkensignal $y(t)$ erzeugt ⇒ Signalrekonstruktion oder D/A–Wandlung entsprechend dem Empfänger–Frequenzgang $H_{\rm E}(f)$.
Das Applet berücksichtigt nicht die PCM–Blöcke „Quantisierung”, „Codierung / Decodierung” und der Digitale Übertragungskanal ist als ideal angenommen.
Daraus ergeben sich folgende Konsequenzen:
- Im Programm ist vereinfachend $y_{\rm A}(t) = x_{\rm A}(t)$ gesetzt.
- Bei geeigneten Systemparametern ist somit auch das Fehlersignal $\varepsilon(t) = y(t)-x(t)\equiv 0$ möglich.
Das Abtasttheorem und die Signalrekonstruktion lassen sich im Frequenzbereich besser erklären. Im Programm werden deshalb auch alle Spektralfunktionen angezeigt:
$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t)$, $X_{\rm A}(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x_{\rm A}(t)$, $Y(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ y(t)$, $E(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ \varepsilon(t).$
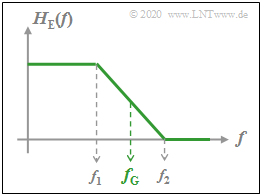
Parameter für den Empfänger–Frequenzgang $H_{\rm E}(f)$ sind die Grenzfrequenz und der Rolloff–Faktor (siehe untere Grafik):
- $$f_{\rm G} = \frac{f_2 +f_1}{2},\hspace{1cm}r = \frac{f_2 -f_1}{f_2 +f_1}.$$
Hinweise:
(1) Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen.
(2) Die Leistungsberechnung erfolgt durch Integration über die jeweilige Periodendauer $T_0$:
- $$P_x = \frac{1}{T_0} \cdot \int_0^{T_0} x^2(t)\ {\rm d}t,\hspace{0.8cm}P_\varepsilon = \frac{1}{T_0} \cdot \int_0^{T_0} \varepsilon^2(t).$$
(3) Die Signalleistung $P_x$ und die Verzerrungsleistung $P_\varepsilon$ werden ebenfalls normiert ausgegeben, was implizit den Bezugswiderstand $R = 1\, \rm \Omega$ voraussetzt.
(4) Daraus kann der Signal–Verzerrungs–Abstand $10 \cdot \lg \ (P_x/P_\varepsilon)$ berechnet werden.
(5) Besteht die Spektralfunktion $X(f)$ bei positiven Frequenzen aus $I$ Diraclinien mit den (eventuell komplexen) Gewichten $X_1$, ... , $X_I$,
so gilt für die Sendeleistung unter Berücksichtigung der spiegelbildlichen Linien bei den negativen Frequenzen:
- $$P_x = 2 \cdot \sum_{i=1}^I |X_k|^2.$$
(6) Entsprechend gilt für die Verzerrungsleistung, wenn die Spektralfunktion $E(f)$ im Bereich $f>0$ genau $J$ Diraclinien mit Gewichten $E_1$, ... , $E_J$ aufweist:
- $$P_\varepsilon = 2 \cdot \sum_{j=1}^J |E_j|^2.$$
Theoretischer Hintergrund
Optimierungskriterium des Matched–Filters
$\text{Definition:}$ Das Matched-Filter – auch Korrelationsfilter genannt – dient zum Nachweis der Signalexistenz.
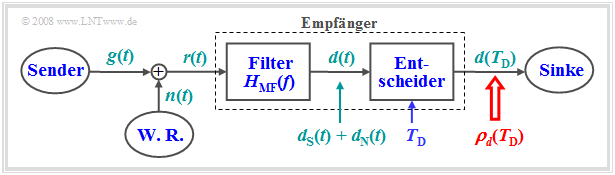
- Der Matched-Filter-Empfänger kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem SNR – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht.
- Zur Herleitung des Matched-Filter-Empfängers wird die skizzierte Anordnung betrachtet.
Für die einzelnen Komponenten gelten folgende Voraussetzungen:
- Der Nutzanteil $g(t)$ des Empfangssignals $r(t)=g(t)+n(t)$ sei impulsförmig und somit energiebegrenzt.
- Das heißt: Das Integral über $\big [g(t)\big ]^2$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
- Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
- Das Filterausgangssignal $d(t)$ setzt sich additiv aus zwei Anteilen zusammen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S$ignal $g(t)$ zurück, der Anteil $d_{\rm N}(t)$ auf das $\rm N$oise $n(t)$.
- Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Hierbei bezeichnen $σ_d^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) Detektionszeitpunkt.
Matched-Filter-Optimierung
Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$.
- Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit der Impulsantwort $h(t)$ und dem Frequenzgang $H(f) =\mathcal{ F}\{h(t)\}$ wie folgt geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm S$ für „Signal”):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
- Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
- Damit lautet das hier vorliegende Optimierungsproblem:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
$\text{Hier zunächst ohne Beweis:}$ Man kann zeigen, dass dieser Quotient für den folgenden Frequenzgang $H(f)$ am größten wird:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit Amplitude $\rm 1\hspace{0.05cm}V$, Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden.
- Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
- Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
Das beste Ergebnis ⇒ das maximale S/N–Verhältnis erzielt man mit dem Matched-Filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$
Das oben angegebene Matched–Filter–Kriterium wird nun schrittweise hergeleitet. Wenn Sie daran nicht interessiert sind, so springen Sie bitte zur Fortsetzungsseite Interpretation des Matched–Filters.
$\text{Herleitung des Matched–Filter–Kriteriums:}$
$(1)$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
$(2)$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
$(3)$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ ergibt sich somit die folgende Schranke:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
$(4)$ Wir setzen für den Filterfrequenzgang nun versuchsweise ein:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$
$(5)$ Dann erhält man aus der obigen Gleichung $(2)$ folgendes Ergebnis:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
$\text{Das heißt:}$
- Mit dem Ansatz $(4)$ für das Matched–Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht.
- Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen.
- Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.
Interpretation des Matched-Filters
Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
Diese beiden Funktionen lassen sich wie folgt interpretieren:
- Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
- Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig.
- Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
- Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
- Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)\equiv 0$ $($„Kausalität”, siehe Buch Lineare zeitinvariante Systeme$)$.
- Der Nutzanteil $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der Energie-AKF $\varphi^{^{\bullet} }_{g} (t )$ und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Bitte beachten Sie:}$ Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.
$\text{Beispiel 2:}$ Wir gehen davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.08cm}ms$ und $\rm 2.5\hspace{0.08cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ gewünscht wird.
Unter diesen Voraussetzungen gilt:
- Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ bis $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$ konstant sein.
- Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
- Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier $\rm si$–förmig.
- Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.
Versuchsdurchführung
Überarbeiten
- Wählen Sie zunächst die Nummer (1, ... , 10) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
- Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen. Auch die ausgegebenen Leistungen sind normierte Größen.
Alles normiert
Für (1) soll voreingestellt sein, ohne dass es in der Aufgabenstellung erwähnt wird: Spalt-TP, $A_h=0.5,\ \Delta t_h=1.6,\ \tau_h=0.8, \ T_D = 2$
(1) Der Eingangsimpuls sei gaußförmig mit $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Welche Einstellung führt zum „Matched–Filter”? Wie groß ist $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$?
- Das Matched–Filter muss ebenfalls einen gaußförmigen Verlauf haben und es muss gelten: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$.
- Das (momentane) Signal–zu–Rauschleistungsverhältnis am Filterausgang ist $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB.
- Mit keinem anderen Filter als dem Matched–Filter ist dieses $\rm SNR$ (oder ein noch besseres) zu erreichen.
(2) Das Matched–Filter bei rechteckförmigen Eingangsimpuls mit $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ ist ein Spalt–Tiefpass ⇒ rechteckförmige Impulsantwort.
Wie groß ist hier $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? Interpretieren Sie alle dargestellten Grafiken und die numerischen Ergebnisse auf verschiedene Art und Weise.
- Die eingestellten Filterparameter sind $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB.
- Die Impulsenergie ist als das Integral über $g(t)^2$ berechenbar ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ ist hier implizit berücksichtigt.
- Eine andere Gleichung lautet: $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. Die Rauschvarianz kann z. B. als Integral über $h(t)^2$ berechnet werden: $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$.
- Das Nutzsignal $d_{\rm S} (t)= g(t) * h(t)$ hat einen dreieckförmigen Verlauf mit dem Maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$.
(3) Es gelten weiter die Einstellungen von (2) mit Ausnahme von $N_0=0.01 $ ⇒ $N_0=0.02$. Welche Veränderungen sind erkennbar?
- Der einzige Unterschied ist die doppelt so große Rauschvarianz $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $T_{\rm D, \ opt} = 0 $ ⇒ $T_{\rm D} = 0.1$. Wie wirkt sich dieser nichtoptimale Detektionszeitpunkt aus?
- Nun ist der Nutzabtastwert $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ kleiner ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. Es ergibt sich eine Verschlechterung um knapp ein dB.
- Für die weiteren Aufgaben wird vom optimalen Detektionszeitpunkt $T_{\rm D, \ opt}$ ausgegangen, wenn nicht explizit etwas anderes angegeben wird.
(5) Es gelten wieder die Einstellungen von (3) mit Ausnahme einer niedrigeren Impulsantwort $A_h = 1 $ ⇒ $A_h = 0.8$. Interpretieren Sie die Veränderungen.
- Es handelt sich auch mit $A_h \ne = A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
- Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber (3) jeweils um den Faktor $0.8^2$ vermindert wird.
(6) Gegenüber (5) wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$?
- Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} =21.94$ dB.
- Der Gewinn von $21.94$ dB gegenüber (5) lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist.
$\text{Hier zunächst ohne Beweis:}$ Man kann zeigen, dass dieser Quotient für den folgenden Frequenzgang $H(f)$ am größten wird:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$}}
(3) Nun gelte $A=1$, $f_0 = \text{5 kHz}$, $\varphi=0$, $f_{\rm A} = \text{10 kHz}$, $f_{\rm G} = \text{5 kHz}$, $r=0$ $($Rechteck–Tiefpass$)$. Interpretieren Sie das Ergebnis der Signalrekonstruktion.
- $X(f)$ besteht aus zwei Diraclinien bei $\pm \text{5 kHz}$ $($Gewicht $0.5)$. Durch die periodische Fortsetzung hat $X_{\rm A}(f)$ Linien bei $\pm \text{5 kHz}$, $\pm \text{15 kHz}$, $\pm \text{25 kHz}$, usw.
- Der Rechteck–Tiefpass entfernt die Linien bei $\pm \text{15 kHz}$, $\pm \text{25 kHz}$, Die Linien bei $\pm \text{5 kHz}$ werden wegen $H_{\rm E}(\pm f_{\rm G}) = H_{\rm E}(\pm \text{5 kHz}) = 0.5$ halbiert
- ⇒ $\text{Gewichte von }X(f = \pm \text{5 kHz})$: $0.5$ | $\text{Gewichte von }X(f_{\rm A} = \pm \text{5 kHz})$: $1.0$; | $\text{Gewichte von }Y(f = \pm \text{5 kHz})$: $0.5$ ⇒ $Y(f)=X(f)$.
- Die Signalrekonstruktion funktioniert also auch hier perfekt $(P_\varepsilon = 0)$. Das gilt auch für die Phase $\varphi=180^\circ$ ⇒ $x(t) = -A \cdot \cos (2\pi \cdot f_0 \cdot t)$.
(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $\varphi=30^\circ$. Interpretieren Sie die Unterschiede gegenüber der Einstellung (3) ⇒ $\varphi=0^\circ$.
- Die Phasenbeziehung geht verloren. Das Sinkensignal $y(t)$ verläuft cosinusförmig $(\varphi_y=0^\circ)$ mit um $\cos(\varphi_x)$ kleinerer Amplitude als das Quellensignal $x(t)$.
- Begründung im Frequenzbereich: Bei der periodische Fortsetzung von $X(f)$ ⇒ $X_{\rm A}(f)$ sind nur die Realteile zu addieren. Die Imaginärteile löschen sich aus.
- Die $f_0$–Diraclinie von $Y(f)$ ist reell, die von $X(f)$ komplex und die von $E(f)$ imaginär ⇒ $\varepsilon(t)$ verläuft minus–sinusförmig ⇒ $P_\varepsilon = 0.125$.
(5) Verdeutlichen Sie sich nochmals das Ergebnis von (4) im Vergleich zu den Einstellungen $f_0 = \text{5 kHz}$, $\varphi=30^\circ$, $f_{\rm A} = \text{11 kHz}$, $f_{\rm G} = \text{5.5 kHz}$.
- Bei dieser Einstellung hat das $X_{\rm A}(f)$–Spektrum auch einen positiven Imaginärteil bei $\text{5 kHz}$ und einen negativen Imaginärteil gleicher Höhe bei $\text{6 kHz}$.
- Der Rechteck–Tiefpass mit der Grenzfrequenz $\text{5.5 kHz}$ entfernt diesen zweiten Anteil. Somit ist bei dieser Einstellung $Y(f) =X(f)$ ⇒ $P_\varepsilon = 0$.
- Jede $f_0$–Schwingung beliebiger Phase ist fehlerfrei aus seinen Abtastwerten rekonstruierbar, falls $f_{\rm A} = 2 \cdot f_{\rm 0} + \mu, \ f_{\rm G}= f_{\rm A}/2$ $($beliebig kleines $\mu>0)$.
- Bei wertkontinuierlichem Spektrum mit $X(|f|> f_0) \equiv 0$ ⇒ $\big[$keine Diraclinien bei $\pm f_0 \big ]$ genügt grundsätzlich die Abtastrate $f_{\rm A} = 2 \cdot f_{\rm 0}$.
(6) Es gelten weiter die Einstellungen von (3) und (4) mit Ausnahme von $\varphi=90^\circ$. Interpretieren Sie die Darstellungen im Zeit– und Frequenzbereich.
- Das Quellensignal wird genau bei seinen Nulldurchgängen abgetastet ⇒ $x_{\rm A}(t) \equiv 0$ ⇒ $y(t) \equiv 0$ ⇒ $\varepsilon(t)=-x(t)$ ⇒ $P_\varepsilon = P_x$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=0\ \rm dB$.
- Beschreibung im Frequenzbereich: Wie in (4) löschen sich die Imaginärteile von $X_{\rm A}(f)$ aus. Auch die Realteile von $X_{\rm A}(f)$ sind wegen des Sinusverlaufs Null.
(7) Nun betrachten wir das $\text {Quellensignal 2}$. Die weiteren Parameter seien $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2.5 kHz}$, $r=0$. Interpretieren Sie die Ergebnisse.
- Das Quellensignal besitzt Spektralanteile bis $\pm \text{2 kHz}$. Die Signalleistung ist $P_x = 2 \cdot \big[0.1^2 + 0.25^2+0.15^2\big]= 0.19 $.
- Mit der Abtastrate $f_{\rm A} = \text{5 kHz}$ sowie den Empfängerparametern $f_{\rm G} = \text{2.5 kHz}$ und $r=0$ funktioniert die Signalrekonstruktion perfekt: $P_\varepsilon = 0$.
- Ebenso mit dem Trapez–Tiefpass mit $f_{\rm G} = \text{2.5 kHz}$, wenn für den Rolloff–Faktor gilt: $r \le 0.2$.
(8) Was passiert, wenn die Grenzfrequenz $f_{\rm G} = \text{1.5 kHz}$ des Rechteck–Tiefpasses zu klein ist? Interpretieren Sie insbesondere das Fehlersignal $\varepsilon(t)=y(t)-x(t)$.
- Das Fehlersignal $\varepsilon(t)=-0.3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t -60^\circ)=0.3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t +120^\circ)$ ist gleich dem (negierten) Signalanteil bei $\text{2 kHz}$. Stimmt das?
- Die Verzerrungsleistung ist $P_\varepsilon(t)=2 \cdot 0.15^2= 0.045$ und der Signal–zu–Verzerrungsabstand $10 \cdot \lg \ (P_x/P_\varepsilon)=10 \cdot \lg \ (0.19/0.045)= 6.26\ \rm dB$.
(9) Was passiert, wenn die Grenzfrequenz $f_{\rm G} = \text{3.5 kHz}$ des Rechteck–Tiefpasses zu groß ist? Interpretieren Sie insbesondere das Fehlersignal $\varepsilon(t)=y(t)-x(t)$.
- Das Fehlersignal $\varepsilon(t)=0.3 \cdot \cos(2\pi \cdot \text{3 kHz} \cdot t +60^\circ)$ ist nun gleich dem vom Tiefpass nicht entfernten $\text{3 kHz}$–Anteil des Sinkensignals $y(t)$. Stimmt das?
- Gegenüber der Teilaufgabe (8) verändert sich die Frequenz von $\text{2 kHz}$ auf $\text{3 kHz}$ und auch die Phasenbeziehung.
- Die Amplitude dieses $\text{3 kHz}$–Fehlersignals ist gleich der Amplitude des $\text{2 kHz}$–Anteils von$x(t)$. Auch hier gilt $P_\varepsilon(t)= 0.045$, $10 \cdot \lg \ (P_x/P_\varepsilon)= 6.26\ \rm dB$.
(10) Abschließend betrachten wir das $\text {Quellensignal 4}$ $($Anteile bis $\pm \text{4 kHz})$, sowie $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2.5 kHz}$, $0 \le r\le 1$. Interpretation der Ergebnisse.
- Bis zum Rolloff–Faktor $r=0.2$ funktioniert die Signalrekonstruktion perfekt $(P_\varepsilon = 0)$. Erhöht man $r$, so nimmt $P_\varepsilon$ kontinuierlich zu und $10 \cdot \lg \ (P_x/P_\varepsilon)$ ab.
- Mit $r=1$ werden die Signalfrequenzen $\text{0.5 kHz}$, ..., $\text{4 kHz}$ abgeschwächt, umso mehr, je höher die Frequenz ist, zum Beispiel $H_{\rm E}(f=\text{4 kHz}) = 0.6$.
- Ebenso beinhaltet $Y(f)$ aufgrund der periodischen Fortsetzung auch Anteile bei den Frequenzen $\text{6 kHz}$, $\text{7 kHz}$, $\text{8 kHz}$, $\text{9 kHz}$ und $\text{9.5 kHz}$.
- Zu den Abtastzeitpunkten $t\hspace{0.05cm}' = n \cdot T_{\rm A}$ stimmen $x(t\hspace{0.05cm}')$ und $y(t\hspace{0.05cm}')$ exakt überein ⇒ $\varepsilon(t\hspace{0.05cm}') = 0$. Dazwischen nicht ⇒ kleine Verzerrungsleistung $P_\varepsilon = 0.008$.
Zur Handhabung des Applets
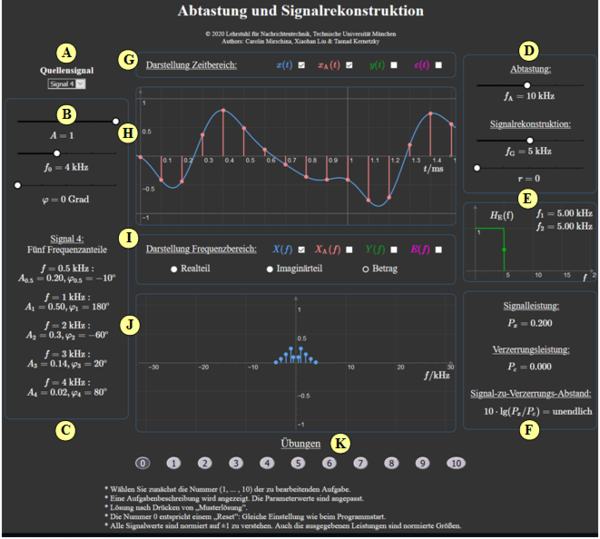
(A) Auswahl eines von vier Quellensignalen
(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)
(C) Ausgabe der verwendeten Programmparameter
(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$
(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$
(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$
(G) Darstellungsauswahl für Zeitbereich
(H) Grafikbereich für Zeitbereich
( I ) Darstellungsauswahl für Frequenzbereich
(J) Grafikbereich für Frequenzbereich
(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger im Rahmen seiner Diplomarbeit (LB) mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.