Applets:Abtastung analoger Signale und Signalrekonstruktion: Unterschied zwischen den Versionen
K (Guenter verschob die Seite Abtastung periodischer Signale und Signalrekonstruktion nach Abtastung analoger Signale und Signalrekonstruktion) |
|||
| Zeile 18: | Zeile 18: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Beschreibung der Abtastung im Zeitbereich=== | |
| − | + | [[Datei:P_ID1120__Sig_T_5_1_S1_neu.png|center|frame|Zur Zeitdiskretisierung des zeitkontinuierlichen Signals $x(t)$]] | |
| − | |||
| − | :$$ | + | Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur: |
| − | \ | + | *Das zeitkontinuierliche Signal sei $x(t)$. |
| − | \hspace{0.05cm}.$$ | + | *Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$. |
| + | *Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) = 0$. | ||
| + | *Die Laufvariable $\nu$ sei [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Reelle_Zahlenmengen|ganzzahlig]]: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $. | ||
| + | *Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$: | ||
| + | |||
| + | :$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$ | ||
| − | + | Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$. | |
| − | + | {{BlaueBox|TEXT= | |
| − | \ | + | $\text{Definitionen:}$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Der | + | Der '''Diracpuls (im Zeitbereich)''' besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$: |
| − | + | ||
| − | * | + | :$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot |
| + | \delta(t- \nu \cdot T_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| + | |||
| + | * Unter '''Abtastung''' verstehen wir im Folgenden die Multiplikation des zeitkontinuierlichen Signals $x(t)$ mit einem solchen '''Diracpuls''': | ||
| + | |||
| + | :$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$}} | ||
| + | Aufgrund dieser Definition ergeben sich für das abgetastete Signal folgende Eigenschaften: | ||
| + | *Das abgetastete Signal zum betrachteten Zeitpunkt $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$. | ||
| + | *Da die Diracfunktion $\delta (t)$ zur Zeit $t = 0$ unendlich ist, sind eigentlich alle Signalwerte $x_{\rm A}(\nu \cdot T_{\rm A})$ ebenfalls unendlich groß. | ||
| + | *Somit ist auch der auf der letzten Seite eingeführte Faktor $K$ eigentlich unendlich groß. | ||
| + | *Zwei Abtastwerte $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ und $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ unterscheiden sich jedoch im gleichen Verhältnis wie die Signalwerte $x(\nu_1 \cdot T_{\rm A})$ und $x(\nu_2 \cdot T_{\rm A})$. | ||
| + | *Die Abtastwerte von $x(t)$ erscheinen in den Impulsgewichten der Diracfunktionen: | ||
| + | |||
| + | :$$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | ||
| + | \delta (t- \nu \cdot T_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| − | + | *Die zusätzliche Multiplikation mit $T_{\rm A}$ ist erforderlich, damit $x(t)$ und $x_{\rm A}(t)$ gleiche Einheit besitzen. Beachten Sie hierbei, dass $\delta (t)$ selbst die Einheit „1/s” aufweist. | |
| − | {{ | ||
| − | |||
| − | |||
| − | |||
| − | + | Die folgenden Seiten werden zeigen, dass diese gewöhnungsbedürftigen Gleichungen durchaus zu sinnvollen Ergebnissen führen, wenn man sie konsequent anwendet. | |
| − | |||
| − | |||
| − | + | ==Diracpuls im Zeit- und im Frequenzbereich== | |
| − | :$$ | + | <br> |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Satz:}$ Entwickelt man den '''Diracpuls''' in eine [[Signaldarstellung/Fourierreihe|Fourierreihe]] und transformiert diese unter Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]] in den Frequenzbereich, so ergibt sich folgende Korrespondenz: | |
| + | |||
| + | :$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | ||
| + | \delta(t- \nu \cdot T_{\rm A} | ||
| + | )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta | ||
| + | (f- \mu \cdot f_{\rm A} ).$$ | ||
| − | + | Hierbei gibt $f_{\rm A} = 1/T_{\rm A}$ den Abstand zweier benachbarter Diraclinien im Frequenzbereich an. }} | |
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Beweis:}$ Die Herleitung der hier angegebenen Spektralfunktion $P_{\delta}(f)$ geschieht in mehreren Schritten: | ||
| − | + | '''(1)''' Da $p_{\delta}(t)$ periodisch mit dem konstanten Abstand $T_{\rm A}$ zwischen zwei Diraclinien ist, kann die [[Signaldarstellung/Fourierreihe#Komplexe_Fourierreihe|(komplexe) Fourierreihendarstellung]] angewendet werden: | |
| + | |||
| + | :$$p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} D_{\mu} \cdot | ||
| + | {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} } | ||
| + | \hspace{0.3cm}{\rm mit}\hspace{0.3cm} | ||
| + | D_{\mu} = \frac{1}{T_{\rm A} } \cdot \int_{-T_{\rm A}/2 | ||
| + | }^{+T_{\rm A}/2}p_{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} | ||
| + | \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$ | ||
| − | + | '''(2)''' Im Bereich von $–T_{\rm A}/2$ bis $+T_{\rm A}/2$ gilt für den Diracpuls im Zeitbereich: $p_{\delta}(t) = T_{\rm A} \cdot \delta(t)$. Damit kann man für die komplexen Fourierkoeffizienten schreiben: | |
| − | :$$\ | + | :$$D_{\mu} = \int_{-T_{\rm A}/2 |
| − | \ | + | }^{+T_{\rm A}/2}{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} |
| − | < | + | \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$ |
| + | '''(3)''' Unter Berücksichtigung der Tatsache, dass für $t \neq 0$ der Diracimpuls Null ist und für $t = 0$ der komplexe Drehfaktor gleich $1$, gilt weiter: | ||
| + | :$$D_{\mu} = \int_{- T_{\rm A}/2 | ||
| + | }^{+T_{\rm A}/2}{\delta}(t) \hspace{0.1cm} {\rm d}t = 1\hspace{0.5cm}{\Rightarrow}\hspace{0.5cm} | ||
| + | p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} {\rm e}^{ {\rm j} \hspace{0.05cm} | ||
| + | \cdot 2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.05cm}. | ||
| + | $$ | ||
| + | '''(4)''' Der [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz im Frequenzbereich]] lautet mit $f_{\rm A} = 1/T_{\rm A}$: | ||
| + | :$${\rm e}^{ {\rm j} \hspace{0.05cm} | ||
| + | \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm} | ||
| + | f_{\rm A}\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | ||
| + | \delta | ||
| + | (f- \mu \cdot f_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| + | '''(5)''' Wendet man das Ergebnis auf jeden einzelnen Summanden an, so erhält man schließlich: | ||
| + | |||
| + | :$$P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta | ||
| + | (f- \mu \cdot f_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| + | <div align="right">q.e.d.</div>}} | ||
| − | |||
| − | + | Das Ergebnis besagt: | |
| + | *Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$. | ||
| + | *Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$. | ||
| + | *$P_{\delta}(f)$ besteht ebenfalls aus unendlich vielen Diracimpulsen, nun aber im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$. | ||
| + | *Die Abstände der Diraclinien in der Zeit– und Frequenzbereichsdarstellung folgen demnach dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Reziprozit.C3.A4tsgesetz_von_Zeitdauer_und_Bandbreite|Reziprozitätsgesetz]]: | ||
| + | :$$T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | [[Datei:P_ID1121__Sig_T_5_1_S3_NEU.png|right|frame|Diracpuls im Zeit- und Frequenzbereich]] |
| − | $\text{ | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 1:}$ Die Grafik verdeutlicht die obigen Aussagen für | ||
| + | *$T_{\rm A} = 50\,{\rm µs}$, | ||
| + | *$f_{\rm A} = 1/T_{\rm A} = 20\,\text{kHz}$ . | ||
| − | |||
| − | |||
| − | |||
| − | + | Man erkennt aus dieser Skizze auch die unterschiedlichen Impulsgewichte von $p_{\delta}(t)$ und $P_{\delta}(f)$.}} | |
| − | + | ===Prinzip und Motivation=== | |
| + | <br> | ||
| + | Viele Nachrichtensignale sind analog und damit gleichzeitig [[Signaldarstellung/Klassifizierung_von_Signalen#Zeitkontinuierliche_und_zeitdiskrete_Signale|zeitkontinuierlich]] und [[Signaldarstellung/Klassifizierung_von_Signalen#Wertkontinuierliche_und_wertdiskrete_Signale|wertkontinuierlich]]. Soll ein solches Analogsignal mittels eines Digitalsystems übertragen werden, so sind folgende Vorverarbeitungsschritte erforderlich: | ||
| + | *die '''Abtastung''' des Nachrichtensignals $x(t)$, die zweckmäßigerweise – aber nicht notwendigerweise – zu äquidistanten Zeitpunkten erfolgt ⇒ '''Zeitdiskretisierung''', | ||
| + | *die '''Quantisierung''' der Abtastwerte, um so die Anzahl $M$ der möglichen Werte auf einen endlichen Wert zu begrenzen ⇒ '''Wertdiskretisierung'''. | ||
| − | + | Die Quantisierung wird erst im Kapitel [[Modulationsverfahren/Pulscodemodulation|Pulscodemodulation]] des Buches „Modulationsverfahren” im Detail behandelt. | |
| − | + | [[Datei:P_ID1120__Sig_T_5_1_S1_neu.png|center|frame|Zur Zeitdiskretisierung des zeitkontinuierlichen Signals $x(t)$]] | |
| − | |||
| − | |||
| − | * | + | Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur: |
| − | :$$ | + | *Das zeitkontinuierliche Signal sei $x(t)$. |
| + | *Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$. | ||
| + | *Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) = 0$. | ||
| + | *Die Laufvariable $\nu$ sei [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Reelle_Zahlenmengen|ganzzahlig]]: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $. | ||
| + | *Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$: | ||
| + | |||
| + | :$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$ | ||
| − | + | Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$. | |
| − | |||
| − | |||
| − | + | ==Frequenzbereichsdarstellung== | |
| − | + | <br> | |
| − | + | Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Faltung_im_Frequenzbereich|Faltungssatzes]]. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht: | |
| + | |||
| + | :$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | ||
| + | X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$ | ||
| + | Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie: | ||
| + | |||
| + | :$$X(f) \star \delta | ||
| + | (f- \mu \cdot f_{\rm A} | ||
| + | )= X (f- \mu \cdot f_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| − | {{ | + | Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich: |
| − | + | ||
| + | :$$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta | ||
| + | (f- \mu \cdot f_{\rm A} | ||
| + | ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} | ||
| + | )\hspace{0.05cm}.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer '''periodischen Fortsetzung''' von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$.}} | ||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
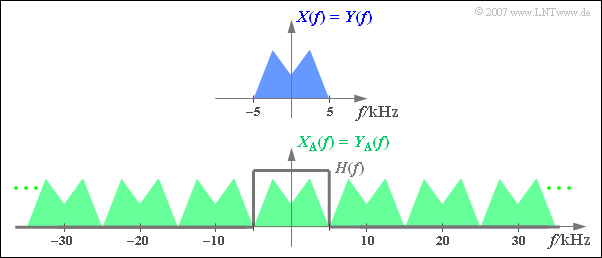
| + | $\text{Beispiel 2:}$ | ||
| + | Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$, das Frequenzen bis $5 \text{ kHz}$ beinhaltet. | ||
| − | : | + | [[Datei:P_ID1122__Sig_T_5_1_S4_neu.png|center|frame|Spektrum des abgetasteten Signals]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$, also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$. | |
| − | + | *Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile. | |
| − | + | *Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.}} | |
| − | |||
| − | |||
| + | ==Signalrekonstruktion== | ||
| + | <br> | ||
| + | Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden. Betrachten wir zum Beispiel das folgende System: | ||
| − | + | [[Datei:P_ID1123__Sig_T_5_1_S5a_neu.png|center|frame|Signalabtastung und Signalrekonstruktion]] | |
| − | |||
| − | + | *Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet. | |
| − | + | *Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor. | |
| − | + | *Die Frage ist nun, wie der Block '''Signalrekonstruktion''' zu gestalten ist, damit auch $y(t) = x(t)$ gilt. | |
| − | + | ||
| − | + | ||
| − | + | Die Lösung ist relativ einfach, wenn man die Spektralfunktionen betrachtet: Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch einen Tiefpass mit dem [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Frequenzgang]] $H(f)$, der | |
| − | + | [[Datei:P_ID1124__Sig_T_5_1_S5b_neu.png|right|frame|Frequenzbereichsdarstellung der Signalrekonstruktion]] | |
| − | + | *die tiefen Frequenzen unverfälscht durchlässt: | |
| − | + | :$$H(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm | |
| − | + | NF}\hspace{0.05cm},$$ | |
| + | *die hohen Frequenzen vollständig unterdrückt: | ||
| + | :$$H(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm | ||
| + | NF}\hspace{0.05cm}.$$ | ||
| + | |||
| + | Weiter ist aus der Grafik zu erkennen, dass der Frequenzgang $H(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann, | ||
| + | *beispielsweise linear abfallend (gestrichelter Verlauf) | ||
| + | *oder auch rechteckförmig, | ||
| + | |||
| + | |||
| + | solange die beiden oben genannten Bedingungen erfüllt sind. | ||
<br clear=all> | <br clear=all> | ||
| − | + | ==Das Abtasttheorem== | |
| − | + | <br> | |
| − | + | Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde. | |
| − | + | ||
| − | + | Aus der Grafik der [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Signalrekonstruktion|letzten Seite]] erkennt man, dass folgende Bedingung erfüllt sein muss: | |
| − | + | ||
| − | + | :$$f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$$ | |
| − | + | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$, so kann dieses aus seinem abgetasteten Signal nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist: | |
| − | + | :$$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$$ | |
| − | + | ||
| − | :$$ | + | Für den Abstand zweier Abtastwerte muss demnach gelten: |
| − | + | ||
| − | * | + | :$$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$$}} |
| − | + | ||
| − | + | ||
| − | + | Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen, | |
| − | + | *so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten | |
| − | + | *ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden. | |
| − | [[Datei: | + | |
| − | + | ||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 3:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$. | |
| − | * | + | [[Datei:P_ID1125__Sig_T_5_1_S6_neu.png|right|frame|Abtasttheorem im Frequenzbereich]] |
| − | + | <br>Zusätzlich eingezeichnet ist der Frequenzgang $H(f)$ des Tiefpasses zur Signalrekonstruktion, dessen Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss. | |
| − | * | + | |
| − | + | ||
| − | + | *Mit jedem anderen $f_{\rm G}$–Wert ergäbe sich $Y(f) \neq X(f)$. | |
| + | *Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$–Anteile. | ||
| + | * Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$. | ||
<br clear=all> | <br clear=all> | ||
| + | Wäre die Abtastung beim Sender mit einer Abtastrate $f_{\rm A} < 10\,\text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \,{\rm µ s}$, so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.}} | ||
| + | ''Hinweis'': Zu der hier behandelten Thematik gibt es ein interaktives Applet: | ||
| + | [[Applets:Abtastung_periodischer_Signale_und_Signalrekonstruktion_(Applet)|Abtastung analoger Signale und Signalrekonstruktion]] | ||
<br clear=all> | <br clear=all> | ||
==Versuchsdurchführung== | ==Versuchsdurchführung== | ||
Version vom 3. Februar 2020, 17:07 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Das Applet verdeutlicht das Gram–Schmidt–Verfahren. Dieses ermöglicht, eine Menge $\{s_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , s_M(t)\}$ energiebegrenzter Signale mit Hilfe von $N \le M$ orthonormalen Basisfunktionen $\varphi_1(t), \hspace{0.05cm} \text{...} \hspace{0.05cm} , \varphi_N(t)$ in folgender Form darzustellen:
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} \text{...}\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} \text{...} \hspace{0.1cm}, N \hspace{0.05cm}.$$
Der vektorielle Repräsentant der Musterfunktion $s_1(t)$ lautet dann: $$\mathbf{s}_i = \big( s_{i1}\hspace{0.05cm}, \hspace{0.3cm}s_{i2}\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm},\hspace{0.05cm} s_{iN} \big ).$$
Das Applet zeigt alle Grafiken, die zum Verständnis des Gram–Schmidt–Verfahrens erforderlich sind, und als jeweiliges Ergebnis
- die 2D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=2$,
- die 3D–Darstellung der $M$ vektoriellen Repräsentanten, falls $N=3$.
Theoretischer Hintergrund
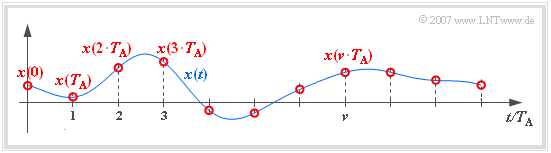
Beschreibung der Abtastung im Zeitbereich
Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur:
- Das zeitkontinuierliche Signal sei $x(t)$.
- Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$.
- Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) = 0$.
- Die Laufvariable $\nu$ sei ganzzahlig: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $.
- Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$:
- $$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$
Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$.
$\text{Definitionen:}$
Der Diracpuls (im Zeitbereich) besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$:
- $$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
- Unter Abtastung verstehen wir im Folgenden die Multiplikation des zeitkontinuierlichen Signals $x(t)$ mit einem solchen Diracpuls:
- $$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$
Aufgrund dieser Definition ergeben sich für das abgetastete Signal folgende Eigenschaften:
- Das abgetastete Signal zum betrachteten Zeitpunkt $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$.
- Da die Diracfunktion $\delta (t)$ zur Zeit $t = 0$ unendlich ist, sind eigentlich alle Signalwerte $x_{\rm A}(\nu \cdot T_{\rm A})$ ebenfalls unendlich groß.
- Somit ist auch der auf der letzten Seite eingeführte Faktor $K$ eigentlich unendlich groß.
- Zwei Abtastwerte $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ und $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ unterscheiden sich jedoch im gleichen Verhältnis wie die Signalwerte $x(\nu_1 \cdot T_{\rm A})$ und $x(\nu_2 \cdot T_{\rm A})$.
- Die Abtastwerte von $x(t)$ erscheinen in den Impulsgewichten der Diracfunktionen:
- $$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
- Die zusätzliche Multiplikation mit $T_{\rm A}$ ist erforderlich, damit $x(t)$ und $x_{\rm A}(t)$ gleiche Einheit besitzen. Beachten Sie hierbei, dass $\delta (t)$ selbst die Einheit „1/s” aufweist.
Die folgenden Seiten werden zeigen, dass diese gewöhnungsbedürftigen Gleichungen durchaus zu sinnvollen Ergebnissen führen, wenn man sie konsequent anwendet.
Diracpuls im Zeit- und im Frequenzbereich
$\text{Satz:}$ Entwickelt man den Diracpuls in eine Fourierreihe und transformiert diese unter Anwendung des Verschiebungssatzes in den Frequenzbereich, so ergibt sich folgende Korrespondenz:
- $$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$$
Hierbei gibt $f_{\rm A} = 1/T_{\rm A}$ den Abstand zweier benachbarter Diraclinien im Frequenzbereich an.
$\text{Beweis:}$ Die Herleitung der hier angegebenen Spektralfunktion $P_{\delta}(f)$ geschieht in mehreren Schritten:
(1) Da $p_{\delta}(t)$ periodisch mit dem konstanten Abstand $T_{\rm A}$ zwischen zwei Diraclinien ist, kann die (komplexe) Fourierreihendarstellung angewendet werden:
- $$p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} D_{\mu} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} } \hspace{0.3cm}{\rm mit}\hspace{0.3cm} D_{\mu} = \frac{1}{T_{\rm A} } \cdot \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}p_{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$
(2) Im Bereich von $–T_{\rm A}/2$ bis $+T_{\rm A}/2$ gilt für den Diracpuls im Zeitbereich: $p_{\delta}(t) = T_{\rm A} \cdot \delta(t)$. Damit kann man für die komplexen Fourierkoeffizienten schreiben:
- $$D_{\mu} = \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$
(3) Unter Berücksichtigung der Tatsache, dass für $t \neq 0$ der Diracimpuls Null ist und für $t = 0$ der komplexe Drehfaktor gleich $1$, gilt weiter:
- $$D_{\mu} = \int_{- T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \hspace{0.1cm} {\rm d}t = 1\hspace{0.5cm}{\Rightarrow}\hspace{0.5cm} p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} {\rm e}^{ {\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.05cm}. $$
(4) Der Verschiebungssatz im Frequenzbereich lautet mit $f_{\rm A} = 1/T_{\rm A}$:
- $${\rm e}^{ {\rm j} \hspace{0.05cm} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm} f_{\rm A}\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
(5) Wendet man das Ergebnis auf jeden einzelnen Summanden an, so erhält man schließlich:
- $$P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
Das Ergebnis besagt:
- Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$.
- Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$.
- $P_{\delta}(f)$ besteht ebenfalls aus unendlich vielen Diracimpulsen, nun aber im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$.
- Die Abstände der Diraclinien in der Zeit– und Frequenzbereichsdarstellung folgen demnach dem Reziprozitätsgesetz:
- $$T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$$
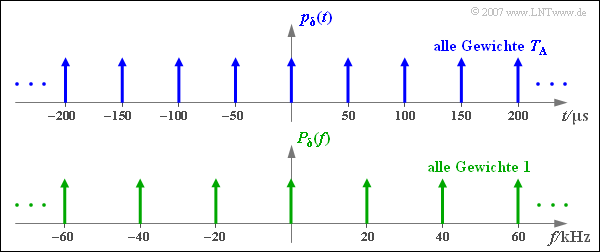
$\text{Beispiel 1:}$ Die Grafik verdeutlicht die obigen Aussagen für
- $T_{\rm A} = 50\,{\rm µs}$,
- $f_{\rm A} = 1/T_{\rm A} = 20\,\text{kHz}$ .
Man erkennt aus dieser Skizze auch die unterschiedlichen Impulsgewichte von $p_{\delta}(t)$ und $P_{\delta}(f)$.
Prinzip und Motivation
Viele Nachrichtensignale sind analog und damit gleichzeitig zeitkontinuierlich und wertkontinuierlich. Soll ein solches Analogsignal mittels eines Digitalsystems übertragen werden, so sind folgende Vorverarbeitungsschritte erforderlich:
- die Abtastung des Nachrichtensignals $x(t)$, die zweckmäßigerweise – aber nicht notwendigerweise – zu äquidistanten Zeitpunkten erfolgt ⇒ Zeitdiskretisierung,
- die Quantisierung der Abtastwerte, um so die Anzahl $M$ der möglichen Werte auf einen endlichen Wert zu begrenzen ⇒ Wertdiskretisierung.
Die Quantisierung wird erst im Kapitel Pulscodemodulation des Buches „Modulationsverfahren” im Detail behandelt.
Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur:
- Das zeitkontinuierliche Signal sei $x(t)$.
- Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$.
- Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) = 0$.
- Die Laufvariable $\nu$ sei ganzzahlig: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $.
- Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$:
- $$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$
Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$.
Frequenzbereichsdarstellung
Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des Faltungssatzes. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht:
- $$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$
Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie:
- $$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich:
- $$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
$\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer periodischen Fortsetzung von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$.
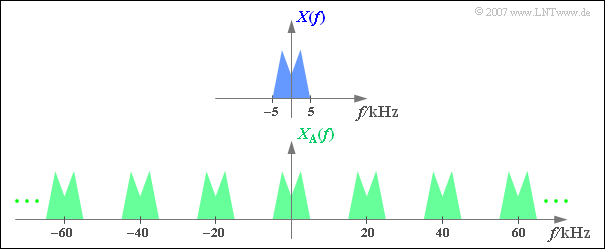
$\text{Beispiel 2:}$ Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$, das Frequenzen bis $5 \text{ kHz}$ beinhaltet.
Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$, also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$.
- Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile.
- Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.
Signalrekonstruktion
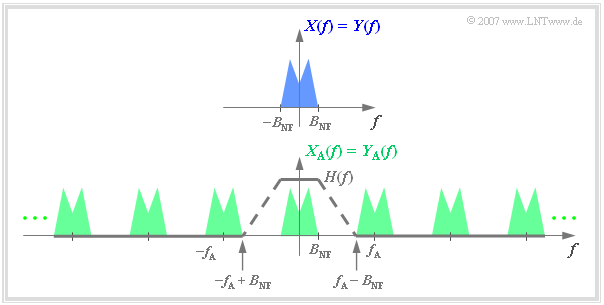
Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden. Betrachten wir zum Beispiel das folgende System:
- Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet.
- Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor.
- Die Frage ist nun, wie der Block Signalrekonstruktion zu gestalten ist, damit auch $y(t) = x(t)$ gilt.
Die Lösung ist relativ einfach, wenn man die Spektralfunktionen betrachtet: Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch einen Tiefpass mit dem Frequenzgang $H(f)$, der
- die tiefen Frequenzen unverfälscht durchlässt:
- $$H(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$$
- die hohen Frequenzen vollständig unterdrückt:
- $$H(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$$
Weiter ist aus der Grafik zu erkennen, dass der Frequenzgang $H(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann,
- beispielsweise linear abfallend (gestrichelter Verlauf)
- oder auch rechteckförmig,
solange die beiden oben genannten Bedingungen erfüllt sind.
Das Abtasttheorem
Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde.
Aus der Grafik der letzten Seite erkennt man, dass folgende Bedingung erfüllt sein muss:
- $$f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$$
$\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$, so kann dieses aus seinem abgetasteten Signal nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist:
- $$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$$
Für den Abstand zweier Abtastwerte muss demnach gelten:
- $$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$$
Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen,
- so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten
- ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden.
$\text{Beispiel 3:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$.
Zusätzlich eingezeichnet ist der Frequenzgang $H(f)$ des Tiefpasses zur Signalrekonstruktion, dessen Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss.
- Mit jedem anderen $f_{\rm G}$–Wert ergäbe sich $Y(f) \neq X(f)$.
- Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$–Anteile.
- Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$.
Wäre die Abtastung beim Sender mit einer Abtastrate $f_{\rm A} < 10\,\text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \,{\rm µ s}$, so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.
Hinweis: Zu der hier behandelten Thematik gibt es ein interaktives Applet:
Abtastung analoger Signale und Signalrekonstruktion
Versuchsdurchführung
Noch anpassen
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
Bis hierher
(1) Es gilt die Einstellung $\rm A$. Interpretieren Sie die ausgegebenen Grafiken. Wählen Sie hierfür „Einzelschritt”.
- Einstellung $\rm A$ beschreibt das $\text{Beispiel 2}$ im Theorieteil. Die Basisfunktion $\varphi_1(t)$ ist identisch mit dem Signal $s_1(t)$, aber mit Signalenergie $E=1$.
- Es gibt hier nur $N=3$ Basisfunktionen, da die Hilfsfunktion $\theta_3(t)$ identisch Null ist.
- Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ können im 3D–Vektorraum abgelesen werden; Beispiel: $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
(2) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm B$. Wählen Sie hierfür und bei den weiteren Aufgaben „Gesamtdarstellung”.
- Auch hier gibt es $N=3$ Basisfunktionen. Bei Änderung auf $s_4 = (-1, \hspace{0.15cm} -1, \hspace{0.25cm} 0)$ nur mehr $N=2$.
(3) Bei der Einstellung $\rm C$ ist die Reihenfolge der Signale gegenüber $\rm B$ vertauscht. Wie wirkt sich das auf die Basisfunktionen aus?
- Auch hier gibt es $N=3$ Basisfunktionen, aber nun andere: Nämlich $\varphi_1(t) = s_1(t)$, $\varphi_2(t) = s_2(t)$, $\varphi_3(t) = s_3(t)$.
(4) Die $M=4$ Signale der Einstellung $\rm D$ lassen sich durch nur $N=2$ Basisfunktionen ausdrücken? Begründen Sie dieses Ergebnis.
- Es gilt $s_3(t) = s_1(t)/4 - s_2(t)/2$ und $s_4(t) = -s_1(t) - s_2(t)$. Das heißt: $s_3(t)$ und $s_4(t)$ liefern keine neuen Basisfunktionen.
(5) Interpretieren Sie die ausgegebenen Grafiken für die Einstellung $\rm E$ im Vergleich zur Einstellung $\rm D$.
- Bei der Einstellung $\rm E$ ist die Reihenfolge der Signale gegenüber der Einstellung $\rm D$ vertauscht. Ähnlich wie zwischen $\rm B$ und $\rm C$.
- Auch diese $M=4$ Signale lassen sich somit durch nur $N=2$ Basisfunktionen ausdrücken, aber durch andere als in der Aufgabe (4).
(6) Welches Ergebnis liefern die vier Signale gemäß der Einstellung $\rm F$?
- Die die Signale $s_1(t)$, ... , $s_4(t)$ basieren alle auf einer einzigen Basisfunktion $\varphi_1(t)$, die formgleich mit $s_1(t)$ ist. Es gilt $N=1$.
- Die vektoriellen Repräsentanten der Signale $s_1(t)$, ... , $s_4(t)$ sind $\pm 0.866$ und $\pm 1.732$. Sie liegen alle auf einer Linie.
(7) Es gilt nun die „M–ASK / BPSK”–Einstellung $\rm G$. Interpretieren Sie das Ergebnis und versuchen Sie, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Vergleicht man die angegebenen Zahlenwerte, so erkennt man, dass eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm A$.
- Der einzige Unterschied ist, dass nun alle Energien nur halb so groß sind wie vorher. Bezüglich der Amplituden wirkt sich das um den Faktor $\sqrt{2}$ aus.
- Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (-1.021, \hspace{0.15cm} -0.289, \hspace{0.15cm} +0.500)$ anstelle von $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
- Bei der Einstellung $\rm H$ sind gegenüber $\rm G$ alle Amplituden verdoppelt. Somit ergibt sich hier wieder $\mathbf{s}_4 = (-1.444, \hspace{0.15cm} -0.408, \hspace{0.15cm} +0.707)$.
(8) Es gelte die „M–ASK / BPSK”–Einstellung $\rm I$. Interpretieren Sie das Ergebnis. Versuchen Sie wieder, einen Zusammenhang zu einer früheren Aufgabe herzustellen.
- Hier wird eine ähnliche Konstellation betrachtet wird wie bei der „Basisband”–Einstellung $\rm C$, aber nun mit nur halb so großen Energien.
- Somit ist nun der vektorielle Repräsentant des unteren Signals $\mathbf{s}_4 = (+0.707, \hspace{0.15cm} -0.707, \hspace{0.15cm} 0.000)$ anstelle von $\mathbf{s}_4 = (+1.000, \hspace{0.15cm} -1.000, \hspace{0.15cm} 0.000)$.
(9) Wählen Sie die Einstellungen $M=4 \text{, nach Spalt–TP, }T_{\rm E}/T = 1$, $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ und $12 \ {\rm dB}$. Interpretieren Sie die Ergebnisse.
- Es gibt nun drei Augenöffnungen. Gegenüber (5) ist also $ö_{\rm norm}$ um den Faktor $3$ kleiner, $\sigma_{\rm norm}$ dagegen nur um etwa den Faktor $\sqrt{5/9)} \approx 0.75$.
- Für $10 \cdot \lg \ E_{\rm B}/N_0 = 10 \ {\rm dB}$ ergibt sich nun die Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2.27\%$ und für $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$ nur mehr $0.59\%$.
(10) Für die restlichen Aufgaben gelte stets $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Betrachten Sie das Augendiagramm für $M=4 \text{, CRO–Nyquist, }r_f = 0.5$.
- In $d_{\rm S}(t)$ müssen alle „Fünf–Symbol–Kombinationen” enthalten sein ⇒ mindestens $4^5 = 1024$ Teilstücke ⇒ maximal $1024$ unterscheidbare Linien.
- Alle $1024$ Augenlinien gehen bei $t=0$ durch nur vier Punkte: $ö_{\rm norm}= 0.333$. $\sigma_{\rm norm} = 0.143$ ist etwas größer als in (9) ⇒ ebenso $p_{\rm U} \approx 1\%$.
(11) Wählen Sie die Einstellungen $M=4 \text{, nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ und variieren Sie $f_{\rm G}/R_{\rm B}$. Interpretieren Sie die Ergebnisse.
- $f_{\rm G}/R_{\rm B}=0.48$ führt zur minimalen Fehlerwahrscheinlichkeit $p_{\rm U} \approx 0.21\%$. Kompromiss zwischen $ö_{\rm norm}= 0.312$ und $\sigma_{\rm norm}= 0.109$.
- Bei zu kleiner Grenzfrequenz dominieren die Impulsinterferenzen. Beispiel: $f_{\rm G}/R_{\rm B}= 0.3$: $ö_{\rm norm}= 0.157; $ $\sigma_{\rm norm}= 0.086$ ⇒ $p_{\rm U} \approx 3.5\%$.
- Bei zu großer Grenzfrequenz dominiert das Rauschen. Beispiel: $f_{\rm G}/R_{\rm B}= 1.0$: $ö_{\rm norm}= 0.333; $ $\sigma_{\rm norm}= 0.157$ ⇒ $p_{\rm U} \approx 1.7\%$.
- Aus dem Vergleich mit (9) erkennt man: Bei Quaternärcodierung ist es günstiger, Impulsinterferenzen zuzulassen.
(12) Welche Unterschiede zeigt das Auge für $M=3 \text{ (AMI-Code), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.48$ gegenüber dem vergleichbaren Binärsystem? Interpretation.
- Der Detektionsgrundimpuls $g_d(t)$ ist in beiden Fällen gleich. Die Abtastwerte sind jeweils $g_0 = 0.771, \ g_1 = 0.114$.
- Beim AMI–Code gibt es zwei Augenöffnungen mit je $ö_{\rm norm}= 1/2 \cdot (g_0 -3 \cdot g_1) = 0.214$. Beim Binärcode: $ö_{\rm norm}= g_0 -2 \cdot g_1 = 0.543$.
- Die AMI–Folge besteht zu 50% aus Nullen. Die Symbole $+1$ und $-1$ wechseln sich ab ⇒ es gibt keine lange $+1$–Folge und keine lange $-1$–Folge.
- Darin liegt der einzige Vorteil des AMI–Codes: Dieser kann auch bei einem gleichsignalfreien Kanal ⇒ $H_{\rm K}(f= 0)=0$ angewendet werden.
(13) Gleiche Einstellung wie in (12), zudem $10 \cdot \lg \ E_{\rm B}/N_0 = 12 \ {\rm dB}$. Analysieren Sie die Fehlerwahrscheinlichkeit des AMI–Codes.
- Trotz kleinerem $\sigma_{\rm norm} = 0.103$ hat der AMI–Code eine höhere Fehlerwahrscheinlichkeit $p_{\rm U} \approx 2\%$ als der Binärcode: $\sigma_{\rm norm} = 0.146, \ p_{\rm U} \approx \cdot 10^{-4}.$
- Für $f_{\rm G}/R_{\rm B}<0.34$ ergibt sich ein geschlossenes Auge $(ö_{\rm norm}= 0)$ ⇒ $p_{\rm U} =50\%$. Beim Binärcode: Für $f_{\rm G}/R_{\rm B}>0.34$ ist das Auge geöffnet.
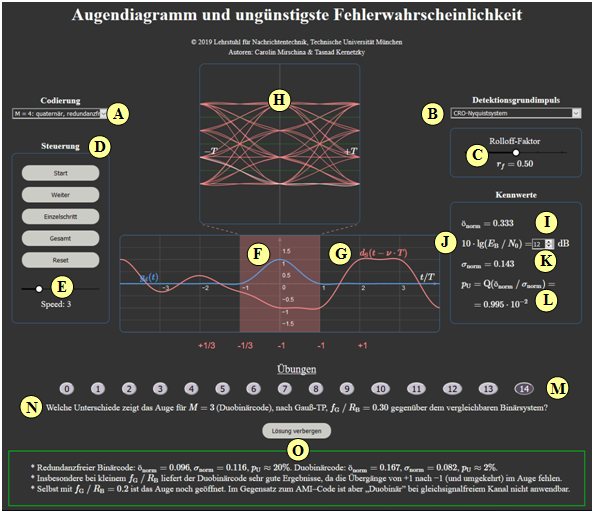
(14) Welche Unterschiede zeigt das Auge für $M=3 \text{ (Duobinärcode), nach Gauß–TP, }f_{\rm G}/R_{\rm B} = 0.30$ gegenüber dem vergleichbaren Binärsystem?
- Redundanzfreier Binärcode: $ö_{\rm norm}= 0.096, \ \sigma_{\rm norm} = 0.116 \ p_{\rm U} \approx 20\% $ Duobinärcode: $ö_{\rm norm}= 0.167, \ \sigma_{\rm norm} = 0.082 \ p_{\rm U} \approx 2\% $.
- Insbesondere bei kleinem $f_{\rm G}/R_{\rm B}$ liefert der Duobinärcode gute Ergebnisse, da die Übergänge von $+1$ nach $-1$ (und umgekehrt) im Auge fehlen.
- Selbst mit $f_{\rm G}/R_{\rm B}=0.2$ ist das Auge noch geöffnet. Im Gegensatz zum AMI–Code ist aber „Duobinär” bei gleichsignalfreiem Kanal nicht anwendbar.
Zur Handhabung des Applets
(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)
(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}
(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)
(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)
(E) Geschwindigkeit der Augendiagrammdarstellung
(F) Darstellung: Detektionsgrundimpuls $g_d(t)$
(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$
(H) Darstellung: Augendiagramm im Bereich $\pm T$
( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)
(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)
(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)
(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)
(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(N) Bereich für die Versuchsdurchführung: Aufgabenstellung
(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2008 von Thomas Großer im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.