Das GWSSUS–Kanalmodell

1. Mobile Kommunikation
2. Frequenzselektive Übertragungskanäle
3. Das GWSSUS–Kanalmodell

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

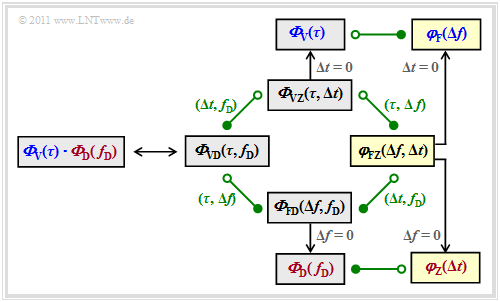
Verallgemeinerte Systemfunktionen zeitvarianter Systeme

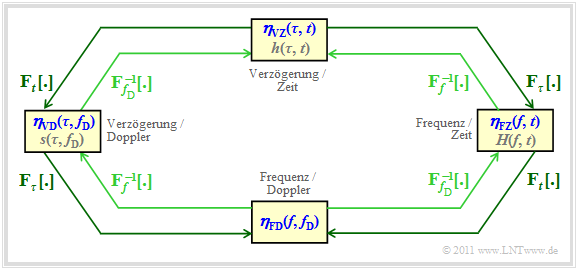
Während es bei linearen zeitinvarianten Systemen  $\rm (LZI)$  mit der Übertragungsfunktion  $H(f)$  und der Impulsantwort  $h(t)$ – nach Umbenennung  $h(\tau)$ – nur zwei das System vollständig beschreibende Systemfunktionen gibt, sind bei zeitvarianten Systemen  $\rm (LZV)$  vier verschiedene Funktionen möglich.  Eine formale Untersscheidung dieser Funktionen hinsichtlich Zeit– und Frequenzbereichsdarstellung durch Klein– und Großbuchstaben ist damit ausgeschlossen.

Deshalb nehmen wir nun eine Nomenklaturänderung vor, die sich wie folgt formalisieren lässt:

• Die vier möglichen Systemfunktionen werden einheitlich mit  $\boldsymbol{\eta}_{12}$  bezeichnet.
  

• Der erste Index ist entweder ein  $\boldsymbol{\rm V}$  $($Verzögerungszeit  $\tau)$  oder ein  $\boldsymbol{\rm F}$  $($Frequenz  $f)$.
  

• Als zweiter Index ist entweder ein  $\boldsymbol{\rm Z}$  $($Zeit  $t)$  oder ein  $\boldsymbol{\rm D}$  $($Dopplerfrequenz  $f_{\rm D})$  möglich.

Zusammenhang zwischen den vier Systemfunktionen

Da beim Mobilfunk im Gegensatz zur leitungsgebundenen Übertragung die Systemfunktionen nicht deterministisch beschrieben werden können, sondern statistische Größen sind, müssen später noch entsprechende Korrelationsfunktionen betrachtet werden. 

Diese bezeichnen wir im Folgenden einheitlich mit  $\boldsymbol{\varphi}_{12}$,  und verwenden gleiche Indizes wie für die Systemfunktionen  $\boldsymbol{\eta}_{12}$.

Diese formalisierten Bezeichnungen sind in der Grafik in blauer Schrift eingetragen.

• Zusätzlich sind die in anderen Kapiteln oder der Literatur verwendeten Bezeichnungen angegeben  (graue Schrift).

• In den weiteren Kapiteln werden diese teilweise ebenfalls benutzt.

• Oben erkennt man die  zeitvariante Impulsantwort  ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t) \equiv h(\tau,\hspace{0.05cm} t)$  im "Verzögerungs–Zeit–Bereich".  Die zugehörige Autokorrelationsfunktion (AKF) ist

\[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \big [ \eta_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \big ]\hspace{0.05cm}. \]

• Zur  "Frequenz–Zeit–Darstellung"  kommt man durch Fouriertransformation bezüglich der Verzögerung  $\tau$.  Man erhält so die  zeitvariante Übertragungsfunktion  ${\eta}_{\rm FZ}(f,\hspace{0.05cm} t) \equiv H(f,\hspace{0.05cm} t)$.  Die Fouriertransformation hinsichtlich  $\tau$  ist in der Grafik durch  ${\rm F}_\tau\hspace{0.05cm}[ \cdot ]$  angedeutet.  Ausgeschrieben lautet das Fourierintegral:

\[\eta_{\rm FZ}(f, \hspace{0.05cm} t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau,\hspace{0.05cm} t) \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}, \hspace{0.3cm} \text{kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) \hspace{0.05cm}.\]

Die AKF dieser zeitvarianten Übertragungsfunktion lautet allgemein:

\[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \big [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \big ]\hspace{0.05cm}.\]

• Die  Scatter–Funktion  ${\eta}_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) \equiv s(\tau,\hspace{0.05cm} f_{\rm D})$  entsprechend dem linken Block beschreibt den Mobilfunkkanal im  "Verzögerungs–Doppler–Bereich".  Der Funktionsparameter  $f_{\rm D}$  bezeichnet hierbei die  Dopplerfrequenz.  Die Scatter–Funktion ergibt sich aus der zeitvarianten Impulsantwort  ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t)$  durch Fouriertransformation bezüglich des zweiten Parameters  $t$:

\[ \eta_{\rm VD}(\tau, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot \eta_{\rm VD}^{\star}(\tau_2, f_{\rm D_2}) \right ] \hspace{0.05cm}.\]

• Abschließend betrachten wir noch die so genannte  frequenzvariante Übertragungsfunktion, also die  "Frequenz–Doppler–Darstellung".  Entsprechend der Grafik gelangt man zu dieser auf zwei Wege:

\[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm FZ}(f, t)\hspace{0.05cm},\]

\[\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.\]

$\text{Hinweise:}$ 

• Die angegebenen Fourier–Zusammenhänge zwischen den Systemfunktionen in der Grafik sind durch die äußeren, dunkelgrünen Pfeile veranschaulicht und mit   ${\rm F}_p\hspace{0.05cm}[\hspace{0.05cm} \cdot \hspace{0.05cm}]$   bezeichnet.  $p$  gibt an, auf welchen Parameter  $\tau$,  $f$,  $t$  oder  $f_{\rm D}$  sich die Fouriertransformation bezieht.

• Die inneren  (helleren)  Pfeile kennzeichnen jeweils die Verknüpfungen über die  inverse Fouriertransformation  (Fourierrücktransformation).  Hierfür verwenden wir die Notation  ${ {\rm F}_p}^{-1}\hspace{0.05cm}[ \hspace{0.05cm} \cdot \hspace{0.05cm} ]$.

• Das Applet  Impulse und Spektren verdeutlicht den Zusammenhang zwischen Zeit– und Frequenzbereich, formelmäßig beschreibbar durch Fouriertransformation und Fourierrücktransformation.

Vereinfachungen aufgrund der GWSSUS–Voraussetzungen

Der allgemeine Zusammenhang zwischen den vier Systemfunktionen ist aufgrund nichtstationärer Effekte sehr kompliziert.

Zusammenhänge zwischen den Beschreibungsfunktionen des GWSSUS–Modells

Gegenüber dem allgemeinen Modell müssen einige Einschränkungen getroffen werden, um zu einem geeigneten Modell für den Mobilfunkkanal zu gelangen, aus dem sich relevante Aussagen für praktische Anwendungen ableiten lassen.

Durch folgende Festlegungen kommt man zum  $\rm GWSSUS$–Modell 
$( \rm G$aussian  $\rm W$ide  $\rm S$ense  $\rm S$tationary  $\rm U$ncorrelated  $\rm S$cattering$)$:

• Der Zufallsprozess der Kanalimpulsantwort  $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$  wird allgemein als komplex  (also Beschreibung im äquivalenten Tiefpassbereich),  gaußisch  $($Kennung  $\rm G)$  sowie als mittelwertfrei  (Rayleigh, nicht Rice, also keine Sichtverbindung)  angenommen.
  

• Der Zufallsprozess sei schwach stationär  ⇒   seine Kenngrößen ändern sich mit der Zeit nur geringfügig, und die AKF  $ {\varphi}_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1,\hspace{0.05cm}\tau_2,\hspace{0.05cm} t_2)$  der zeitvarianten Impulsantwort hängt nicht von den absoluten Zeiten  $t_1$  und  $t_2$  ab, sondern nur von der Zeitdifferenz  $\Delta t = t_2 - t_1$.  Darauf weist die Kennung  $\rm WSS$  hin   ⇒   $\rm W$ide $\rm S$ense $\rm S$tationary.
  

• Die einzelnen Echos durch Mehrwegeausbreitung sind unkorreliert, was die Kennung  $\rm US$   ⇒   $\rm U$ncorrelated $\rm S$cattering ausdrückt.

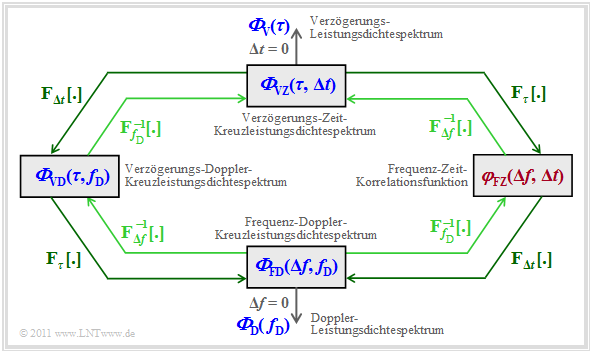
Der Mobilfunkkanal lässt sich gemäß dieser Grafik vollständig beschreiben.  Auf die einzelnen Leistungsdichtespektren  (blau beschriftet)  und die Korrelationsfunktion  (mit roter Schrift)  wird auf den nächsten Seiten im Detail eingegangen.

Autokorrelationsfunktion der zeitvarianten Impulsantwort

Wir betrachten nun die  Autokorrelationsfunktion  $\rm (AKF)$  der zeitvarianten Impulsantwort   ⇒   $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$  genauer.  Es zeigt sich:

• Aufgrund der  $\rm WSS$–Eigenschaft lässt sich mit  $\Delta t = t_2 - t_1$  für die Autokorrelationsfunktion schreiben:

\[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.\]

• Da die Echos als unabhängig voneinander vorausgesetzt wurden  $\rm (US$–Eigenschaft$)$, kann man die Impulsantwort bezüglich den Verzögerungen  $\tau_1$  und  $\tau_2$  als unkorreliert annehmen.  Dann gilt:

\[\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. \]

• Ersetzt man nun  $\tau_1$  durch  $\tau$  und  $\tau_2$  durch  $\tau + \Delta \tau$, so lässt sich diese Autokorrelationsfunktion in folgender Weise darstellen:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]

• Wegen der Ausblendeigenschaft der Diracfunktion verschwindet die AKF für  $\tau_1 \ne \tau_2$   ⇒   $\Delta \tau \ne 0$.

• $ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.1cm}$  ist das  "Verzögerungs–Zeit–Kreuzleistungsdichtespektrum", das von der Verzögerung  $\tau \ (= \tau_1 =\tau_2)$  und von der Zeitdifferenz  $\Delta t = t_2 - t_1$  abhängt.
  
  

$\text{Bitte beachten Sie:}$ 

• Bei dieser Betrachtungsweise hängen Autokorrelationsfunktion  $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$  und Leistungsdichtespektrum  ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $  nicht wie sonst üblich über die Fouriertransformation zusammen, sondern sind über eine Diracfunktion verknüpft:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]

• Nicht alle Symmetrieeigenschaften, die aus dem  Wiener–Chintchine–Theorem  folgen, sind somit auch hier gegeben. Insbesondere ist es durchaus möglich und sogar sehr wahrscheinlich, dass ein solches Leistungsdichtespektrum eine ungerade Funktion ist.

In der Übersicht auf der letzten Seite ist das  Verzögerungs–Zeit–Kreuzleistungsdichtespektrum  ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $  oben in der Mitte zu erkennen.

• Da  $\eta_{\rm VZ}(\tau, t) $  wie jede beliebige  Impulsantwort  die Einheit  $\rm [1/s]$  aufweist, hat die Autokorrelationsfunktion die Einheit  $\rm [1/s^2]$:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot \eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ].\]

• Da aber auch die Diracfunktion mit Zeitargument, also  $\delta(\Delta \tau)$, die Einheit  $\rm [1/s]$  hat, besitzt das Verzögerungs–Zeit–Kreuzleistungsdichtespektrum  ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $  ebenfalls die Einheit $\rm [1/s]$:

\[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.\]

Leistungsdichtespektrum der zeitvarianten Impulsantwort

Verzögerungs–Leistungsdichtespektrum

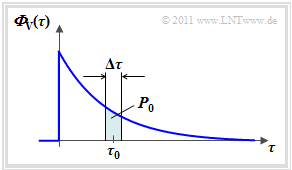
Zum  Verzögerungs–Leistungsdichtespektrum  ${\it \Phi}_{\rm V}(\Delta \tau)$  kommt man, indem man in der Funktion  ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$  den zweiten Parameter  $\Delta t = 0$  setzt.  Die Grafik zeigt einen beispielhaften Verlauf.

Das Verzögerungs–Leistungsdichtespektrum ist eine zentrale Größe für die Beschreibung des Mobilfunkkanals.  Diese weist folgende Eigenschaften auf:

• ${\it \Phi}_{\rm V}(\Delta \tau_0)$  ist ein Maß für die „Leistung” derjenigen Signalanteile, die um  $\tau_0$  verzögert werden.  Es wird hierfür implizit eine Mittelung über alle Dopplerfrequenzen  $(f_{\rm D})$  vorgenommen.
  

• Das Verzögerungs–Leistungsdichtespektrum  ${\it \Phi}_{\rm V}(\Delta \tau)$  hat wie  ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$  die Einheit  $\rm [1/s]$.  Es charakterisiert die Leistungsverteilung über alle möglichen Verzögerungszeiten  $\tau$.
  

• In der Grafik farblich markiert ist die Leistung  $ P_0 \approx {\it \Phi}_{\rm V}(\Delta \tau_0)\cdot \Delta \tau$  solcher Signalanteile, die beim Empfänger über beliebige Pfade mit einer Verzögerung zwischen  $\tau_0 \pm \Delta \tau/2$  eintreffen.
  

• Normiert man das Leistungsdichtespektrum  ${\it \Phi}_{\rm V}(\Delta \tau)$  derart, dass sich die Fläche  $1$  ergibt, so erhält man die  "Wahrscheinlichkeitsdichtefunktion"  $\rm (WDF)$ der Verzögerungszeit:

\[{\rm WDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.\]

Anmerkung zur Nomenklatur:

• Im Buch „Stochastische Signaltheorie” hätten wir diese  Wahrscheinlichkeitsdichtefunktion  mit  $f_\tau(\tau)$  bezeichnet.
• Um den Zusammenhang zwischen  ${\it \Phi}_{\rm V}(\Delta \tau)$  und WDF zu verdeutlichen und Verwechslungen mit der Frequenz  $f$  zu vermeiden, verwenden wir diese Nomenklatur.
  

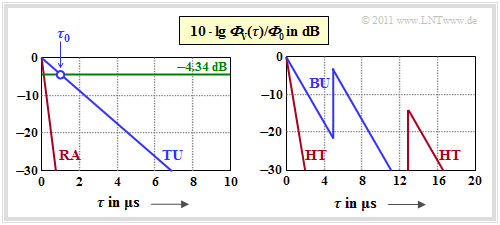
$\text{Beispiel 1: Verzögerungsmodelle nach COST 207}$

In den 1990er Jahren gründete die Europäische Union die Arbeitsgruppe COST 207 mit dem Ziel, standardisierte Kanalmodelle für den zellularen Mobilfunk bereitzustellen.  Hierbei steht „COST” für  European Cooperation in Science and Technology.

In diesem internationalen Gremium wurden Profile für die Verzögerungszeit  $\tau$  entwickelt, basierend auf Messungen und gültig für verschiedene Anwendungsszenarien.  Im Folgenden werden vier verschiedene Verzögerungs–Leistungsdichtespektren angegeben, wobei stets der Normierungsfaktor  ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$  verwendet wird.  Die Grafik zeigt die Verzögerungs–Leistungsdichte dieser Profile in logarithmischer Darstellung:

Verzögerungs–Leistungsdichte nach COST

(1)  Profil $\rm RA$ (englisch "Rural Area")   ⇒   ländliches Gebiet:

\[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}{\rm im \hspace{0.15cm}Bereich}\hspace{0.3cm} 0 < \tau < 0.7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.109\,{\rm µ s}\hspace{0.05cm}.\]

(2)  Profil $\rm TU$ (englisch "Typical Urban")   ⇒   Städte und Vororte:

\[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}{\rm im \hspace{0.15cm}Bereich}\hspace{0.3cm} 0 < \tau < 7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}.\]

(3)  Profil $\rm BU$ (englisch "Bad Urban")   ⇒   ungünstige Bedingungen in Städten:

\[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.5 \cdot {\rm e}^{ (5\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{0.1cm} {\rm für}\hspace{0.3cm} 0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{0.1cm} {\rm für}\hspace{0.3cm} 5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]

(4)  Profil $\rm HT$ (englisch "Hilly Terrain")   ⇒   hügeliges Gebiet und Bergland:

\[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.04 \cdot {\rm e}^{ (15\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{-0.25cm} {\rm für}\hspace{0.3cm} 0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{-0.25cm} {\rm für}\hspace{0.3cm} 15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]

Man erkennt aus den Grafiken:

• Aus den Exponentialfunktionen bei linearer Darstellung werden nun geradlinige Verläufe.

• Bei logarithmischer Darstellung kann man den LDS–Parameter  $\tau_0$  bei  $\rm 10 \cdot lg \ (1/e) = -4.34 \ dB$  ablesen, wie in der Grafik für das  $\rm TU$-Profil eingezeichnet.

• Auf diese vier COST–Profile wird in der  Aufgabe 2.8  noch genauer eingegangen.

AKF und LDS der frequenzvarianten Übertragungsfunktion

Die in der  Übersicht auf der ersten Seite dieses Kapitels  unten dargestellte Systemfunktion  $\eta_{\rm FD}(f, f_{\rm D})$  wird auch  frequenzvariante Übertragungsfunktion  genannt, wobei sich das Adjektiv „frequenzvariant” auf die Dopplerfrequenz bezieht.

Die dazugehörige AKF ist wie folgt definiert:

\[\varphi_{\rm FD}(f_1, f_{\rm D_1}, f_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm FD}(f_1, f_{\rm D_1}) \cdot \eta_{\rm FZ}^{\star}(f_2, f_{\rm D_2}) \right ]\hspace{0.05cm}. \]

Durch ähnliche Überlegungen wie auf der  vorletzten Seite  kann man diese Autokorrelationsfunktion unter GWSSUS–Bedingungen wie folgt darstellen:

\[\varphi_{\rm FD}(\Delta f, \Delta f_{\rm D}) = \delta(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \hspace{0.05cm}.\]

Dabei gilt:

• ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$  ist das so genannte  Frequenz–Doppler–Kreuzleistungsdichtespektrum, das in der Grafik am Seitenende durch gelbe Hinterlegung hervorgehoben ist.
  

• Das erste Argument  $\Delta f = f_2 - f_1$  berücksichtigt, dass AKF und LDS aufgrund der Stationarität nur von der Frequenzdifferenz abhängen.

• Der Faktor  $\delta (\Delta f_{\rm D})$  mit  $\Delta f_{\rm D} = f_{\rm D_2} - f_{\rm D_1}$  drückt die Unkorreliertheit der AKF bezüglich der Dopplerverschiebung aus.
  

• Man kommt von  ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$  zum  Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$, wenn man  $\Delta f= 0$  setzt.

• Das Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$  gibt an, mit welcher Leistung einzelne Dopplerfrequenzen auftreten.
  

• Die Wahrscheinlichkeitsdichte der Dopplerfrequenz ergibt sich aus  ${\it \Phi}_{\rm D}(f_{\rm D})$  durch geeignete Flächennormierung.  Die WDF weist wie  ${\it \Phi}_{\rm D}(f_{\rm D})$  die Einheit  $\rm [1/Hz]$  auf:

Zur Berechnung des Doppler–Leistungsdichtespektrums

\[{\rm WDF}_{\rm D}(f_{\rm D}) = \frac{{\it \Phi}_{\rm D}(f_{\rm D})}{\int_{-\infty }^{+\infty}{\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.15cm}{\rm d}f_{\rm D}} \hspace{0.05cm}.\]

• Oft, so zum Beispiel für eine vertikale Monopulsantenne im isotrop gestreuten Feld, ist  ${\it \Phi}_{\rm D}(f_{\rm D})$  durch das  Jakes–Spektrum  gegeben.
  

Das Frequenz–Doppler–Kreuzleistungsdichtespektrum  ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$  ist gelb hinterlegt.

• Eingezeichnet sind auch die Fourierzusammenhänge zu den benachbarten GWSSUS–Systembeschreibungsfunktionen.
  

• Wir verweisen hier auf das interaktive Applet  Zur Verdeutlichung des Dopplereffekts.

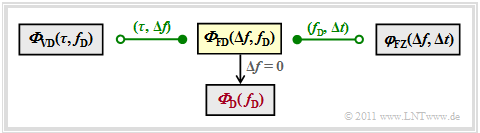
AKF und LDS der Verzögerungs–Doppler–Funktion

Die in der  Übersicht auf der ersten Seite dieses Kapitels  links dargestellte Systemfunktion wurde mit  $\eta_{\rm VD}(\tau, f_{\rm D})$  bezeichnet.  Die AKF dieser Verzögerungs–Doppler–Funktion kann unter Berücksichtigung der GWSSUS–Eigenschaften mit  $\Delta \tau = \tau_2 - \tau_1$  und  $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$  wie folgt geschrieben werden:

\[\varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = \varphi_{\rm VD}(\Delta \tau, \Delta f_{\rm D}) = \delta(\Delta \tau) \cdot {\rm \delta}(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \hspace{0.05cm}.\]

Zu dieser Gleichung ist anzumerken:

• Die erste Diracfunktion  $\delta (\Delta \tau)$  berücksichtigt, dass die Verzögerungen unkorreliert sind („Uncorrelated Scattering”).
• Die zweite Diracfunktion  $\delta (\Delta f_{\rm D})$  folgt aus der Stationarität („Wide Sense Stationary”).
  

• Das Verzögerungs–Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$  – auch  Scatter–LDS  genannt – kann aus  ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$  bzw.  ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$  berechnet werden:

\[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) ={\rm F}_{\Delta t} \big [ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VZ}(\tau, \Delta t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm D} \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta t}\hspace{0.15cm}{\rm d}\Delta t \hspace{0.05cm},\]

\[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\rm F}_{f_{\rm D}}^{-1} \big [ {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \cdot {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \tau \hspace{0.05cm}\cdot \hspace{0.05cm} \Delta f}\hspace{0.15cm}{\rm d}\Delta f \hspace{0.05cm}. \]

• Sowohl die Systemfunktion  $\eta_{\rm VD}(\tau, f_{\rm D})$  als auch die abgeleiteten Funktionen  $\varphi _{\rm VD}(\Delta \tau, \Delta f_{\rm D})$  und  ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$  sind dimensionslos.  Nähere Angaben hierüber finden Sie in der Angabe zu  Aufgabe 2.6.

• Weiterhin ist bei Erfüllung der GWSSUS–Voraussetzungen die Scatterfunktion gleich dem Produkt aus Verzögerungs– und Doppler–Leistungsdichtespektrum:

\[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]

Eindimensionale Beschreibungsfunktionen des GWSSUS–Modells

$\text{Fazit:}$  Die Abbildung fasst die bisherigen Ergebnisse dieses Kapitels zusammen.

Festzuhalten ist:

(1)   Der Einfluss der Verzögerungszeit (Laufzeit)  $\tau$  und der Dopplerfrequenz  $f_{\rm D}$  lässt sich separieren

• in das blaue Leistungsdichtespektrum ${\it \Phi}_{\rm V}(\tau)$, und
• das rote Leistungsdichtespektrum ${\it \Phi}_{\rm D}(f_{\rm D})$.
  

(2)   Das 2D–Verzögerungs–Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$  ist gleich dem Produkt aus diesen beiden Anteilen.

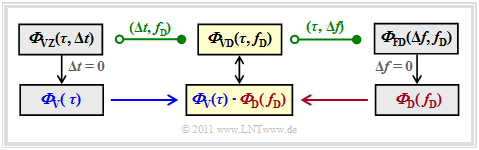
AKF und LDS der zeitvarianten Übertragungsfunktion

Die folgende Grafik zeigt alle Zusammenhänge zwischen den einzelnen Leistungsdichtespektren nochmals in kompakter Form.

Kompakte Zusammenstellung aller GWSSUS–Beschreibungsgrößen

Auf den letzten Seiten wurden dabei bereits behandelt:

• das  Verzögerungs–Zeit–Kreuzleistungsdichtespektrum:

$${\it \Phi}_{\rm VZ}(\tau, \Delta t)\hspace{0.55cm}\Rightarrow \hspace{0.3cm}\text{mit} \hspace{0.2cm}\Delta t = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau),$$

• das  Frequenz–Doppler–Kreuzleistungsdichtespektrum:

$${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{mit} \hspace{0.2cm}\Delta f = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm D}( f_{\rm D}),$$

• das  Verzögerungs–Doppler–Kreuzleistungsdichtespektrum:

$${\it \Phi}_{\rm VD}(\tau, f_{\rm D})= {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.$$

Bisher noch nicht betrachtet wurde die  Frequenz–Zeit–Korrelationsfunktion
(in nebenstehender Grafik gelb markiert):

\[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.\]

Berücksichtigt man wieder die GWSSUS–Vereinfachungen sowie die Identität  $\eta_{\rm FZ}(f, \hspace{0.05cm}t) = H(f, \hspace{0.05cm}t)$, so lässt sich die AKF mit  $\Delta f = f_2 - f_1$  und  $\Delta t = t_2 - t_1$  auch wie folgt schreiben:

\[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_{\rm FZ}(\Delta f, \Delta t) = {\rm E} \big [ H(f, t) \cdot H^{\star}(f + \Delta f, t + \Delta t) \big ]\hspace{0.05cm}.\]

Hierzu ist anzumerken:

• Schon an der Namensgebung ist zu erkennen, dass  $\varphi_{\rm FZ}(\Delta f, \Delta t)$  eine Korrelationsfunktion ist und kein Leistungsdichtespektrum wie die Funktionen  ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$,  ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$  und  ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$.
  

• Die Fourierzusammenhänge mit den benachbarten Funktionen lauten:

\[{\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.05cm}\Delta f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \varphi_{\rm FZ}(\Delta f, \hspace{0.05cm}\Delta t) \hspace{0.2cm} \stackrel{\Delta t,\hspace{0.05cm} f_{\rm D}}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm FD}(\Delta f,\hspace{0.05cm} f_{\rm D}) \hspace{0.05cm}.\]

• Setzt man in dieser 2D– Funktion die Parameter  $\Delta t = 0$  bzw.  $\Delta f = 0$, so ergeben sich die separaten Korrelationsfunktionen für den Frequenz– bzw. den Zeitbereich:

\[\varphi_{\rm F}(\Delta f) = \varphi_{\rm FZ}(\Delta f, \Delta t = 0) \hspace{0.05cm},\]

\[\varphi_{\rm Z}(\Delta t) = \varphi_{\rm FZ}(\Delta f = 0, \Delta t ) \hspace{0.05cm}.\]

• Aus obiger Grafik wird auch deutlich, dass diese Korrelationsfunktionen mit den hergeleiteten Leistungsdichtespektren über die Fouriertransformation korrespondieren:

\[\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}, \hspace{0.4cm}\varphi_{\rm Z}(\Delta t) \hspace{0.2cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]

Kenngrößen des GWSSUS–Modells

Entsprechend den Ergebnissen der letzten Seite wird der Mobilfunkkanal durch

• das Verzögerungs–Leistungsdichtespektrum  ${\it \Phi}_{\rm V}(\tau)$  und
  

• das Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$
  
  

vollständig beschrieben.  Durch geeignete Normierung auf die jeweilige Fläche  $1$  ergeben sich daraus die Dichtefunktionen bezüglich der Verzögerungszeit  $\tau$  bzw. der Dopplerfrequenz  $f_{\rm D}$.

Aus den Leistungsdichtespektren bzw. den zugehörigen Korrelationsfunktionen können Kenngrößen abgeleitet werden.  Die wichtigsten sind hier zusammengestellt:

$\text{Definition:}$  Die  Mehrwegeverbreiterung  (englisch:  Time Delay Spread  oder  Multipath Spread )  $T_{\rm V}$  gibt die Verbreiterung an, die ein Diracimpuls durch den Kanal im statistischen Mittel erfährt.  $T_{\rm V}$  ist definiert als die Standardabweichung  $(\sigma_{\rm V})$  der Zufallsgröße  $\tau$:

\[T_{\rm V} = \sigma_{\rm V} = \sqrt{ {\rm E} \big [ \tau^2 \big ] - m_{\rm V}^2} \hspace{0.05cm}.\]

• Der Mittelwert  $m_{\rm V} = {\rm E}\big[\tau \big]$  ist eine für alle Signalanteile „gleiche mittlere Laufzeit” (englisch:   Average Excess Delay).
• ${\rm E} \big [ \tau^2 \big ] $  ist als quadratischer Mittelwert zu berechnen.

$\text{Definition:}$  Die  Kohärenzbandbreite  $B_{\rm K}$  (englisch:   Coherence Bandwidth )  ist derjenige  $\Delta f$–Wert, bei dem der Frequenz–Korrelationsfunktion betragsmäßig erstmals auf die Hälfte abgesunken ist.

\[\vert \varphi_{\rm F}(\Delta f = B_{\rm K})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm F}(\Delta f = 0)\vert \hspace{0.05cm}.\]

• $B_{\rm K}$  ist ein Maß für die Frequenzdifferenz, um die sich zwei harmonische Schwingungen mindestens unterscheiden müssen, damit sie völlig andere Kanalübertragungseigenschaften vorfinden.
• Ist die Signalbandbreite  $B_{\rm S} <B_{\rm K}$, so werden alle Spektralanteile durch den Kanal annähernd gleich verändert.
  Das heißt:   Genau dann liegt nichtfrequenzselektives Fading vor.

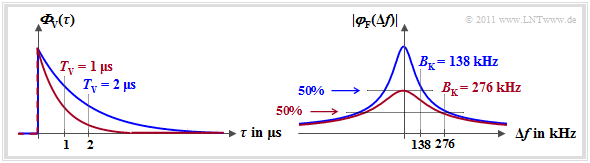
$\text{Beispiel 2:}$  In der Grafik links dargestellt ist die Verzögerungsleistungsdichte  ${\it \Phi}_{\rm V}(\tau)$

Mehrwegeverbreiterung und Kohärenzbandbreite

• mit  $T_{\rm V} = 1 \ \rm µs$  (rote Kurve),
• mit  $T_{\rm V} = 2 \ \rm µ s$  (blaue Kurve).

In der rechten  $\varphi_{\rm F}(\Delta f)$–Darstellung sind die Kohärenzbandbreiten eingezeichnet:

• $B_{\rm K} = 276 \ \rm kHz$  (rote Kurve),
• $B_{\rm K} = 138 \ \rm kHz$  (blaue Kurve).

Man erkennt aus diesen Zahlenwerten:

• Die aus  ${\it \Phi}_{\rm V}(\tau)$  berechenbare Mehrwegeverbreiterung  $T_{\rm V}$  steht mit der durch  $\varphi_{\rm F}(\Delta f)$  festgelegten Kohärenzbandbreite  $B_{\rm K}$  in einem festen Verhältnis zueinander:   $B_{\rm K} \approx 0.276/T_{\rm V}$.
• Die oft  benutzte Näherung  $B_{\rm K}\hspace{0.02cm}' \approx 1/T_{\rm V}$  ist hingegen bei exponentiellem  ${\it \Phi}_{\rm V}(\tau)$  sehr ungenau.

Betrachten wir nun die Zeitvarianz–Kenngrößen, die von der Zeit–Korrelationsfunktion  $\varphi_{\rm Z}(\Delta t)$  bzw. vom Doppler–Leistungsdichtespektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$  abgeleitet werden:

$\text{Definition:}$  Die  Korrelationsdauer $T_{\rm D}$  (englisch:   Coherence Time )  gibt die Zeit an, die im Mittel vergehen muss, bis der Kanal seine Übertragungseigenschaften aufgrund der Zeitvarianz völlig geändert hat.  Deren Definition ist ähnlich wie die Definition der Kohärenzbandbreite:

\[\vert \varphi_{\rm Z}(\Delta t = T_{\rm D})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm Z}(\Delta t = 0)\vert \hspace{0.05cm}.\]

$\text{Definition:}$  Die  Dopplerverbreiterung  $B_{\rm D}$  (oder „Fading–Bandbreite”, englisch:   Doppler Spread )  ist die mittlere Frequenzverbreiterung, die die einzelnen spektralen Signalanteile erfahren.  Bei der Berechnung geht man ähnlich vor wie bei der Mehrwegeverbreiterung, indem man die Dopplerverbreiterung  $B_{\rm D}$  als die Standardabweichung der Zufallsgröße  $f_{\rm D}$  berechnet:

\[B_{\rm D} = \sigma_{\rm D} = \sqrt{ {\rm E} \left [ f_{\rm D}^2 \right ] - m_{\rm D}^2} \hspace{0.05cm}.\]

• Zunächst ist aus  ${\it \Phi}_{\rm D}(f_{\rm D})$  durch Flächennormierung auf  $1$  die Doppler–WDF zu ermitteln.
• Daraus ergeben sich die mittlere Dopplerverschiebung  $m_{\rm D} = {\rm E}[f_{\rm D}]$  und die Standardabweichung  $\sigma_{\rm D}$.

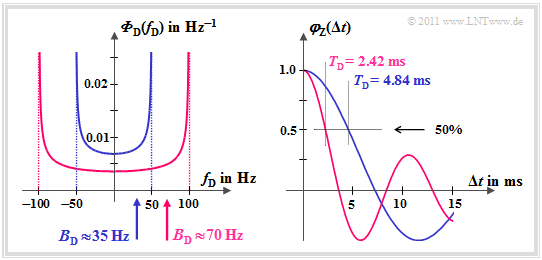
$\text{Beispiel 3:}$  Die Grafik gilt für einen zeitvarianten Kanal ohne Direktkomponente. Links dargestellt ist das  Jakes–Spektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$.

Dopplerverbreiterung und Korrelationsdauer

Die Dopplerverbreiterung  $B_{\rm D}$  lässt sich daraus ermitteln:

\[f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.45cm} B_{\rm D} \approx 35\,{\rm Hz} \hspace{0.05cm},\]

\[f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.2cm} B_{\rm D} \approx 70\,{\rm Hz} \hspace{0.05cm}.\]

Die Zeitkorrelationsfunktion  $\varphi_{\rm Z}(\Delta t)$  als die Fourierrücktransformierte von  ${\it \Phi}_{\rm D}(f_{\rm D})$  ist rechts skizziert.

Bei den gegebenen Randbedingungen lautet diese mit der Besselfunktion:

\[\varphi_{\rm Z}(\Delta t \hspace{-0.05cm} = \hspace{-0.05cm}T_{\rm D}) \hspace{-0.05cm}= \hspace{-0.05cm} {\rm J}_0(2 \pi \hspace{-0.05cm} \cdot \hspace{-0.05cm} f_{\rm D,\hspace{0.05cm}max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\Delta t ).\]

• Die Korrelationsdauer der blauen Kurve ist  $T_{\rm D} = 4.84 \ \rm ms$.
• Für  $f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}$  ist die Korrelationsdauer nur halb so groß.
• Allgemein gilt im vorliegenden Fall:   $B_{\rm D} \cdot T_{\rm D}\approx 0.17$.

Simulation gemäß dem GWSSUS–Modell

Das abschließend nur kurz dargelegte Monte–Carlo–Verfahren zur Simulation eines GWSSUS–Mobilfunkkanals basiert auf Arbeiten von Rice [Ric44] und Höher [Höh90].

• Die 2D–Impulsantwort wird durch eine Summe aus $M$ komplexen Exponentialfunktionen dargestellt.  $M$  ist als die Anzahl unterschiedlicher Pfade interpretierbar:

\[h(\tau,\ t)= \frac{1}{\sqrt {M}} \cdot \sum_{m=1}^{M} \alpha_m \cdot \delta (t - \tau_m) \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \phi_{m} }\cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi f_{{\rm D},\hspace{0.05cm} m} t} \hspace{0.05cm}. \]

• Vor Beginn werden die Verzögerungen  $\tau_m$,  die Dämpfungsfaktoren  $\alpha_m$,  die gleichverteilten Phasen  $\phi_m$  und die Dopplerfrequenzen  $f_{{\rm D},\hspace{0.05cm} m}$  nach den GWSSUS–Vorgaben „ausgewürfelt”.  Grundlage für das Auswürfeln der Dopplerfrequenzen  $f_{{\rm D},\hspace{0.05cm} m}$  ist das  Jakes–Spektrum  ${\it \Phi}_{\rm D}(f_{\rm D})$,  das  – geeignet normiert –  gleichzeitig die WDF der Dopplerfrequenzen angibt.
  

• Wegen  ${\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})$  ist für alle  $m$  die Verzögerungszeit  $\tau_m$  unabhängig von der Dopplerfrequenz  $f_{{\rm D},\hspace{0.05cm} m}$.  Für den terrestrischen Landmobilfunk gilt dies mit guter Näherung.  Für das Auswürfeln der Parameter  $\alpha_m$  und  $\tau_m$,  die das Verzögerungs–Leistungsdichtespektrum  $ {\it \Phi}_{\rm V}(\tau)$  bestimmen, stehen die  COST–Profile  $\rm RA$  (Rural Area),  $\rm TU$  (Typical Urban),  $\rm BU$  (Bad Urban)  und  $\rm HT$  (Hilly Terrain) zur Verfügung.
  

• Je größer bei der Simulation die Anzahl  $M$  unterschiedlicher Pfade gewählt wird, um so besser wird eine reale Impulsantwort durch obige Gleichung angenähert.  Die höhere Simulationsgenauigkeit geht allerdings auf Kosten der Simulationsdauer.  In der Literatur werden für  $M$  günstige Werte zwischen  $100$  und  $600$  angegeben.
  

Zeitvariante Übertragungsfunktion
$($Betragsquadrat,  simuliert$)$

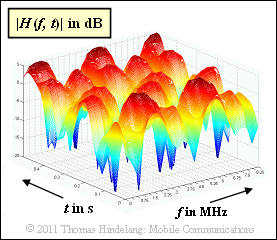
$\text{Beispiel 4:}$  Die Grafik aus [Hin08] zeigt ein Simulationsergebnis:   Als 2D–Plot ist  $20 \cdot \lg \vert H(f, \hspace{0.1cm}t)\vert$  dargestellt, wobei die zeitvariante Übertragungsfunktion  $H(f, \hspace{0.1cm}t)$  in diesem Tutorial auch mit  $\eta_{\rm FZ}(f, \hspace{0.1cm}t)$  bezeichnet wird.

Der Simulation liegen folgende Parameter zugrunde:

• Die Zeitvarianz entsteht durch eine Bewegung mit  $v = 3 \ \rm km/h$.
• Die Trägerfrequenz ist  $f_{\rm T} = 2 \ \rm GHz$.
  

• Die maximale Verzögerungszeit beträgt  $\tau_{\rm max} \approx 0.4 \ \rm µ s$.
• Daraus ergibt sich nach der Näherung für die Kohärenzbandbreite  $B_{\rm K}\hspace{0.02cm}' \approx 2.5 \ \rm MHz$.
  

• Die maximale Dopplerfrequenz ist  $f_\text{D, max} \approx 5.5 \ \rm Hz$.
• Die Dopplerverbreiterung ergibt sich zu  $B_{\rm D} \approx 4 \ \rm Hz$.

Aufgaben zum Kapitel

Aufgabe 2.5: Scatter-Funktion

Aufgabe 2.5Z: Mehrwege-Szenario

Aufgabe 2.6: Einheiten bei GWSSUS

Aufgabe 2.7: Kohärenzbandbreite

Aufgabe 2.7Z: Kohärenzbandbreite des LZI–Zweiwegekanals

Aufgabe 2.8: COST-Verzögerungsmodelle

Aufgabe 2.9: Korrelationsdauer