Aufgabe 5.1: Fehlerabstandsverteilung
Ein jedes digitales Kanalmodell kann in gleicher Weise beschrieben werden durch
- die Fehlerfolge $〈e_{\rm \nu}〉$,
- durch die Fehlerabstandsfolge $〈a_{\rm \nu '}〉$.
Beispielhaft betrachten wir die Folgen:
- $$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < \hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, ... \hspace{-0.1cm}> \hspace{0.05cm},$$
- $$< \hspace{-0.1cm}a_{\nu\hspace{0.05cm} '} \hspace{-0.15cm}> \ = \ <\hspace{-0.1cm}2, 3, 1, 4, 2, 5, 1, 1, 3, 4, 1, 2, ... \hspace{-0.1cm}> \hspace{0.05cm}.$$
Man erkennt daraus beispielsweise:
- Der Fehlerabstand $a_2 = 3$ bedeutet, dass zwischen dem ersten und dem zweiten Fehler zwei fehlerfreie Symbole liegen.
- $a_3 = 1$ deutet dagegen darauf hin, dass nach dem zweiten direkt ein dritter Fehler folgt.
Die unterschiedlichen Laufindizes ($\nu$ und $\nu '$, jeweils beginnend mit $1$) sind erforderlich, da keine Synchronität zwischen der Fehlerabstandsfolge und der Fehlerfolge besteht.
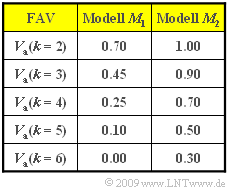
In der Grafik ist für zwei verschiedene Modelle $M_1$ und $M_2$ die Fehlerabstandsverteilung (FAV)
- $$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$
angegeben. Diese Tabelle soll in dieser Aufgabe ausgewertet werden.
Hinweis: Die Aufgabe gehört zum Themengebiet des Kapitels Beschreibungsgrößen digitaler Kanalmodelle.
Fragebogen
Musterlösung
- $e_{\rm 16} \underline {= 0}$,
- $e_{\rm 17} \underline {= 1}$,
- $e_{\rm 18} \undelrine {= 1}$.
(2) Aus der Definitionsgleichung folgt bereits
- $$V_a(k = 1) = {\rm Pr}(a \ge 1)\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$
(3) Es gilt ${\rm Pr}(a = k) = V_a(k) \, –V_a(k+1)$. Daraus erhält man für die einzelnen Wahrscheinlichkeiten:
- $${\rm Pr}(a = 1)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(1) - V_a(2) = 1 - 0.7\hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$
- $${\rm Pr}(a = 2)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(2) - V_a(3) = 0.7 - 0.45 \hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm},$$
- $${\rm Pr}(a = 3)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(3) - V_a(4) = 0.45 - 0.25 \hspace{0.15cm}\underline {= 0.2}\hspace{0.05cm},$$
- $${\rm Pr}(a = 4)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(4) - V_a(5) = 0.25 - 0.10 \hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$
- $${\rm Pr}(a = 5)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(5) - V_a(6) = 0.10 - 0 \hspace{0.15cm}\underline {= 0.10}\hspace{0.05cm}.$$
(4) Aus $V_a(k=6) = {\rm Pr}(a ≥ 6) = 0$ folgt für den maximalen Fehlerabstand direkt $k_{\rm max} = 5$.
(5) Mit den unter (3) berechneten Wahrscheinlichkeiten ergibt sich für den gesuchten Erwartungswert:
- $${\rm E}[a] = \sum_{k = 1}^{5} k \cdot {\rm Pr}(a = k) = 1 \cdot 0.3 +2 \cdot 0.25 +3 \cdot 0.2 +4 \cdot 0.15 +5 \cdot 0.1\hspace{0.15cm}\underline { = 2.5} \hspace{0.05cm}.$$
(6) Die mittlere Fehlerwahrscheinlichkeit ist der Kehrwert des mittleren Fehlerabstands: $p_{\rm M} \underline {= 0.4}$.
(7) Die Aussage 1 stimmt, da ${\rm Pr}(a = 1) = V_1(1) \, – V_(2) = 0$ ist.
- Die zweite Aussage ist nicht sicher, da $V_a(6)$ nur die Summe der Wahrscheinlichkeiten ${\rm Pr}(a ≥ 6)$ angibt, aber nicht ${\rm Pr}(a = 6)$ allein. Nur mit der zusätzlichen Angabe $V_a(7) = 0$ würde die Aussage 2 zutreffen.
- Ebenso ist für den Erwartungswert ${\rm E}[a] augrund fehlender Angaben keine endgültige Aussage möglich. Mit $V_a(7 = 0)$ würde sich :{\rm E}[a] = 2 \cdot 0.1 +3 \cdot 0.2 +4 \cdot 0.2 +5 \cdot 0.2 +6 \cdot 0.3= 4.4$$ ergeben. Ohne diese Angabe ist nur die Aussage ${\rm E}[a] ≥ 4.4$ möglich. Damit gilt aber für die mittlere Fehlerwahrscheinlichkeit die Bedingung $p_{\rm M} < 1/4.4 < 0.227$ ⇒ Die Aussage 3 trifft also mit Sicherheit nicht zu. Mit Sicherheit stimmt nur die Aussage 1.