Aufgabe 2.08: Generatorpolynome für Reed-Solomon
Aus LNTwww
Version vom 10. Oktober 2022, 15:24 Uhr von Guenter (Diskussion | Beiträge)
In der "Aufgabe 2.7" sollten Sie die Codeworte des $\rm RSC \, (7, \, 3, \, 5)_8$ über ein Polynom ermitteln. Man kann aber das Codewort $\underline{c}$ auch aus dem Informationswort $\underline{u}$ und der Generatormatrix $\mathbf{G}$ gemäß der folgenden Gleichung bestimmen:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$
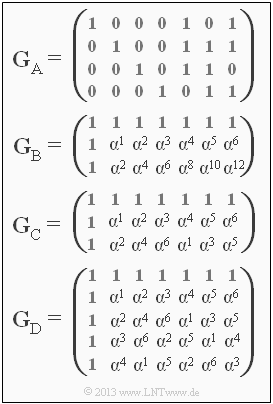
- Zwei dieser Generatormatrizen beschreiben den $\rm RSC \, (7, \, 3, \, 5)_8$. In der Teilaufgabe (1) ist explizit gefragt, welche.
- Eine weitere Generatormatrix gehört zum $\rm RSC \, (7, \, 5, \, 3)_8$, der in der Teilaufgabe (3) betrachtet wird.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Definition und Eigenschaften von Reed–Solomon–Codes".
- Weitere Informationen zu den Reed–Solomon–Codes finden Sie in der "Aufgabe 2.7".
Fragebogen
Musterlösung
(1) Richtig sind die Lösungsvorschläge 2 und 3 ⇒ Matrizen $\mathbf{G}_{\rm B}$ und $\mathbf{G}_{\rm C}$.
- In der Matrix $\mathbf{G}_{\rm C}$ wurden bereits die erlaubten Umformungen $\alpha^8 = \alpha, \ \alpha^{10} = \alpha^3$ und $\alpha^{12} = \alpha^5$ berücksichtigt.
- Die Matrix $\mathbf{G}_{\rm A}$ gilt für den $(7, \, 5, \, 3)$–Hamming–Code und $\mathbf{G}_{\rm D}$ gehört zum $\rm RSC \, (7, \, 5, \, 3)_8$. Siehe hierzu Teilaufgabe (3).
(2) Beim $\rm RSC \, (7, \, 3, \, 5)_8$ werden in jedem Codierschritt $k = 3$ Informationssymbole verarbeitet, im Codierschritt 1 gemäß der Angabe die Symbole $\alpha^4, \ 1$ und $\alpha^3$.
- Mit der Generatormatrix $\mathbf{G}_{\rm C}$ gilt somit:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm C} = \begin{pmatrix} \alpha^4 & 1 & \alpha^3 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm}. $$
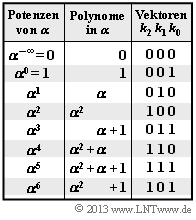
- Damit ergibt sich entsprechend der nebenstehenden Hilfstabelle:
- $$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 = (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2}= (110) + (010) + (110) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{2} + \alpha^{3}\cdot \alpha^{4}= (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{3} + \alpha^{3}\cdot \alpha^{6}=$ (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$
- $$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{4} + \alpha^{3}\cdot \alpha^{1} = \alpha^{4} \hspace{0.05cm},$$
- $$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{5} + \alpha^{3}\cdot \alpha^{3}= (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{6} + \alpha^{3}\cdot \alpha^{5}= (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$
- Man erhält das genau gleiche Ergebnis wie in der (4) von "Aufgabe 2.7". Richtig sind die Lösungsvorschläge 1 und 2.
- Es gilt also nicht $c_6 = 0$, sondern $c_6 = 1$.
(3) Beim $\rm RSC \, (7, \, 5, \, 3)_8$ ist das Informationswort $\underline{u} = (u_0, \, u_1, \, u_2, \, u_3, \, u_4)$ zu berücksichtigen.
- Mit der Generatormatrix $\mathbf{G}_{\rm D}$ erhält man:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm D} = \begin{pmatrix} \alpha^4 & 1 & \alpha^3 & 0 & \alpha^6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5 & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 & \alpha^{6} & \alpha^{3} \end{pmatrix}\hspace{0.05cm}. $$
- Daraus folgt:
- $$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 + 0 \cdot 1 + \alpha^{6}\cdot 1= (110) + (001) + (011) + (000) + (101) = (001) = 1 \hspace{0.05cm},$$
- $$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2} \right ] + 0 \cdot \alpha^{3} + \alpha^{6}\cdot \alpha^{4}= \left [ \alpha^{3} \right ] + \alpha^{3} = 0 \hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass der Klammerausdruck $[ \ \text{...} \ ]$ genau dem Ergebnis $c_1$ der Teilaufgabe (2) entspricht.
- Entsprechendes wird auch bei den folgenden Berechnungen berücksichtigt:
- $$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{3} \right ] + \alpha^{6}\cdot \alpha^{1}= \left [ \alpha^{3} \right ] + \alpha^{7} = (011) + (001) = (010) = \alpha^{1} \hspace{0.05cm},$$
- $$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ 1 \right ] + \alpha^{6}\cdot \alpha^{5}= \left [ 1 \right ] + \alpha^{4}= (001) + (110) = (111) = \alpha^{5} \hspace{0.05cm},$$
- $$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4} \right ] + \alpha^{6}\cdot \alpha^{2}= \left [ \alpha^{4} \right ] + \alpha^{1} = (110) + (010) = (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{2} \right ] + \alpha^{6}\cdot \alpha^{6}= \left [ \alpha^{2} \right ] + \alpha^{5} = (100) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ 1 \right ] + \alpha^{6}\cdot \alpha^{3}= \left [ 1 \right ] + \alpha^{2} = (001) + (100) = (101) = \alpha^{6} \hspace{0.05cm}.$$
- Das heißt: Alle Lösungsvorschläge sind richtig.