Aufgabe 2.07: Reed–Solomon–Code (7, 3, 5) zur Basis 8

• Zurück zum Buch

$\rm GF(2^3)$–Darstellung als Potenzen, Polynome, Vektoren

Der hier betrachtete Reed–Solomon–Code mit der Bezeichnung  $\rm RSC \, (7, \, 3, \, 5)_8$

• codiert einen Informationsblock  $\underline{u} = (u_0, \, u_1, \, u_2)$  von  $k = 3$  Symbolen,  wobei  $u_0, \, u_1, \, u_2 ∈ \rm GF(2^3)$  keine Bits,  sondern Symbole darstellen;

• erzeugt ein Codewort  $\underline{c} = (c_0, \, c_1,\hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6)$  der Länge  $n = 7$  mit Codesymbolen  $c_i$  ebenfalls aus dem Galoisfeld  $\rm GF(2^3)$,

• besitzt die freie Distanz  $d_{\rm min} = n - k + 1 = 5$,  so dass bis zu   $e = 4$   Symbolfehler erkannt und bis zu   $t = 2$   Symbolfehler korrigiert werden können.

Die Elemente des zugrunde liegenden Galoisfeldes lauten:

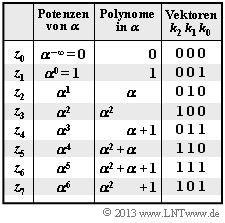
$${\rm GF}(2^3) = \{\hspace{0.1cm} 0\hspace{0.05cm},\hspace{0.1cm} 1 \hspace{0.05cm},\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}.$$

1. Diese Elemente lassen sich entsprechend der Grafik auch als Polynome oder als Koeffizientenvektoren darstellen.
2. Man erkennt aus obiger Tabelle,  dass alle  $u_i ∈ \rm GF(2^3)$  und alle  $c_i ∈ \rm GF(2^3)$  auch durch  $m = 3 \ \rm Bit$  charakterisiert werden können,  zum Beispiel  $\alpha^4$  durch  „$110$”.

Sie sollen in dieser Aufgabe für die binäre Eingangsfolge

$$110 \hspace{0.09cm}001\hspace{0.09cm} 011\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 000\hspace{0.09cm} 111 \hspace{0.05cm} \text{...}$$

den Codiervorgang nachvollziehen.  Beachten Sie dabei:

• Der Reed–Solomon–Coder arbeitet blockweise.  Im ersten Codierschritt werden aus den drei ersten Informationssymbolen die Codesymbole  $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$  erzeugt,  im zweiten Schritt dann aus dem Informationsblock  $\underline{u} = (u_3, \, u_4, \, u_5)$  die Symbole  $(c_7, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_{13})$  des zweiten Codewortes, usw.

• Man beschreibt den Informationsblock  $\underline{u}$  durch das Polynom   $u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2$   vom Grad  $2$.  Allgemein ergibt sich für das Galoisfeld  $\rm GF(2^m)$  der Grad des Polynoms zu  $m - 1$.

• Die Codesymbole  $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , c_6$  erhält man,  indem in das Polynom  $u(x)$  alle Elemente  $x$  von  $\rm GF(2^3)$  mit Ausnahme des Nullelementes eingesetzt werden:

$${\rm GF}(2^3)\hspace{-0.01cm}\setminus \hspace{-0.01cm}\{ 0\} = \{\hspace{0.1cm}\alpha^{0}\hspace{0.05cm},\hspace{0.1cm} \alpha^1\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm} \alpha^{4} \hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.1cm}\}\hspace{0.05cm}.$$

• Formal lässt sich der  $\rm RSC \, (7, \, 3, \, 5)_8$  wie folgt beschreiben:

$$C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}u(\alpha^{2})\hspace{0.1cm} \big ) \hspace{0.1cm} \big | \hspace{0.2cm} u(x) = \sum_{i = 0}^{2} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^3) \Big \} \hspace{0.05cm}.$$

Hinweise:

• Die vorliegende Aufgabe gehört zum Kapitel  "Definition und Eigenschaften von Reed–Solomon–Codes".

• Die  "Aufgabe 2.8"  ist ähnlich strukturiert wie diese,  aber zur Generierung eines Codewortes  $\underline{c}$  wird dann die Generatormatrix  $\mathbf{G}$  herangezogen.

Fragebogen

1

Wie lautet der binäre Informationsblock im ersten Codierschritt?

	$\underline{u}_{\rm bin} = (110)$,
	$\underline{u}_{\rm bin} = (110_|001_|011)$,
	$\underline{u}_{\rm bin} = (110_|001_|0)$.

2

Wie lauten die Informationssymbole im ersten Codierschritt?

	$u_0 = \alpha^4$,
	$u_0 = 0$,
	$u_1 = \alpha^6$,
	$u_1 = \alpha^0$,
	$u_2 = \alpha^3$,
	$u_2 = \alpha^2$.

3

Wie lautet der Informationsblock als Polynom  $u(x)$?

	$u(x) = \alpha^3 \cdot x + x^2 + \alpha^4 \cdot x^3$,
	$u(x) = \alpha^3 + x + \alpha^4 \cdot x^2$,
	$u(x) = \alpha^4 + x + \alpha^3 \cdot x^2$.

4

Wie lauten die Codesymbole  $c_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} ,\ c_6$  für den ersten Codierschritt.

	$c_0 = \alpha^2$,
	$c_1 = \alpha^3$,
	$c_2 = \alpha^3$,
	$c_3 = 1$,
	$c_4 = \alpha^2$,
	$c_5 = \alpha^4$,
	$c_6 = 1$.

5

Wie lautet das binäre Codewort?

	$\underline{c}_{\rm bin} = 100_|011_|011_|001_|110_|100_|001$,
	$\underline{c}_{\rm bin} = 011_|011_|001_|110_|100_|001_|100$,
	$\underline{c}_{\rm bin} = 100_|111_|0$.

6

Welche Aussagen gelten für den zweiten Codierschritt?

	Es gilt  $u_0 = u_1 = u_2 = 0$.
	Es gilt  $u(x) = 1$.
	Das Codewort  $\underline{c} ∈ \rm GF(2^3)$  besteht aus sieben Nullsymbolen.
	Das binäre Codewort   $\underline{c}_{\rm bin} ∈ \rm GF(2)$  besteht aus 21 Nullen.

Musterlösung

Musterlösung

(1)  Richtig ist der  Lösungsvorschlag 2:

• Alle Informationssymbole entstammen hier dem Galoisfeld  $\rm GF(2^3)$.  In Binärschreibweise wird jedes Symbol durch drei Bit dargestellt.

• Aufgrund des RS–Codeparameters  $k = 3$  besteht ein Informationsblock aus drei Informationssymbolen:  $\underline{u} = (u_0, \, u_1, \, u_2)$.

• Dementsprechend beinhaltet der binäre Informationsblock  $\underline{u}_{\rm bin}$  genau  $3 \cdot 3 = 9$  Bit.

(2)  Entsprechend der Tabelle auf der Angabenseite besteht folgender Zusammenhang zwischen dem Koeffizientenvektor und der Exponentialdarstellung:

$$(110) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_0 = \alpha^{4}\hspace{0.05cm},\hspace{0.6cm} (001) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_1 = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.6cm} (011) \hspace{0.1cm} \Rightarrow \hspace{0.2cm} u_2 = \alpha^{3}\hspace{0.05cm}.$$

• Richtig sind also die  Lösungsvorschläge 1, 4 und 5.

• Der Informationsblock im ersten Codierschritt lautet:  $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$.

(3)  In Polynomdarstellung ergibt sich für den Informationsblock  $\underline{u} = (\alpha^4, \, 1, \, \alpha^3)$:

$$u(x) = u_0 + u_1 \cdot x + u_2 \cdot x^2 = \alpha^{4} + x + \alpha^{3}\cdot x^2 \hspace{0.05cm}.$$

• Richtig ist demnach der  Lösungsvorschlag 3.

• Der erste Lösungsvorschlag kann schon allein deshalb nicht stimmen,  da der Polynomgrad höchstens  $2$  sein kann,  wenn alle Informations– und Codesymbole aus  $\rm GF(2^3)$  entstammen.

(4)  Für die Codesymbole erhält man mit der Polynomdarstellung entsprechend der Angabenseite:

$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{0} = 1) = \alpha^{4} + 1 + \alpha^{3}\cdot 1^2 = (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$

$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{1}) = \alpha^{4} + \alpha + \alpha^{5}= (110) + (010) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$

$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{2}) = \alpha^{4} + \alpha^{2} + \alpha^{7}= (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$

$$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{3}) = \alpha^{4} + \alpha^{3} + \alpha^{9}= (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$

$$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{4}) = \alpha^{4} + \alpha^{4} + \alpha^{11} = \alpha^{4} \hspace{0.05cm},$$

$$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{5}) = \alpha^{4} + \alpha^{5} + \alpha^{13}= (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$

$$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u(x = \alpha^{6}) = \alpha^{4} + \alpha^{6} + \alpha^{15}= (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$

• Richtig sind also die  Lösungsvorschläge 1, 2, 3, 4, 7.

• Die angegebenen Lösungen zu 5 und 6 sind genau vertauscht.

(5)  Richtig ist der  erste Lösungsvorschlag:

• Es ergibt sich aus dem Ergebnis der Teilaufgabe  (4)  und der Zuordnung

$$\alpha^2 ↔ 100, \ \alpha^3 ↔ 011, \ \alpha^3 ↔ 011, \ 1 ↔ 001, \ \alpha^4 ↔ 110, \ \alpha^2 ↔ 100, \ 1 ↔ 001.$$

• Der letzte Lösungsvorschlag kann schon allein deshalb nicht stimmen,  da das binäre Codewort aus  $n \cdot m = 7 \cdot 3 = 21$  Bit bestehen muss.

• Selbst wenn Sie in der Teilaufgabe  (4)  nur das Ergebnis  $c_0 = \alpha^2$  ermittelt haben,  so wissen Sie schon,  dass hier der Vorschlag 2 nicht der richtige sein kann.

(6)  Die  Aussagen 1, 3, 4  sind richtig:

• Die Bit 10, ... , 18 der Eingangssequenz sind alle  $0$  und damit auch die Informationssymbole  $u_0, \ u_1, \ u_2 ∈ \rm GF(2^3)$.

• Dementsprechend ist auch  $u(x) = 0$,  so dass alle Codesymbole  $c_i = u(x = \alpha^i)$  dem Nullsymbol entsprechen  $($Index: $0 ≤ i ≤ 6)$.

• Die binäre Codefolge besteht somit aus  $n \cdot m = 21$  Nullen.