|
|
| Zeile 78: |
Zeile 78: |
| | \hspace{0.05cm},\hspace{0.3cm}\text{mit}$$ | | \hspace{0.05cm},\hspace{0.3cm}\text{mit}$$ |
| | :$$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$ | | :$$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$ |
| − | ${\rm I_0}( ... )$ bezeichnet die [https://de.wikipedia.org/wiki/Besselsche_Differentialgleichung modifizierte Besselfunktion].
| |
| − | :$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta
| |
| − | + {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − |
| |
| − | *Da jedes Bit genau auf ein Symbol abgebildet wird, ist die mittlere Bitfehlerwahrscheinlichkeit $p_{\rm B}$ genau so groß:
| |
| − |
| |
| − | ::<math>p_{\rm B}
| |
| − | = {\rm Q} \left ( \sqrt{{E_{\rm S}}/{N_0}}\right ) = {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.</math>
| |
| | | | |
| | Wir betrachten [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|On–Off–Keying]] (bzw. 2–ASK) im äquivalenten Tiefpassbereich. | | Wir betrachten [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|On–Off–Keying]] (bzw. 2–ASK) im äquivalenten Tiefpassbereich. |
| Zeile 132: |
Zeile 119: |
| | | | |
| | Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool [[Applets:On-Off-Keying|Nichtkohärentes On–Off–Keying]] bestimmen.}} | | Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool [[Applets:On-Off-Keying|Nichtkohärentes On–Off–Keying]] bestimmen.}} |
| − | ===Zusammenhang $x(t)\Leftrightarrow X(f)$===
| |
| − | *Der Zusammenhang zwischen der Zeitfunktion $x(t)$ und dem Spektrum $X(f)$ ist durch das [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|erste Fourierintegral]] gegeben:
| |
| − | :$$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm}
| |
| − | \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$
| |
| − |
| |
| − | *Um aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ berechnen zu können, benötigt man das [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_zweite_Fourierintegral|zweite Fourierintegral]]:
| |
| − | :$$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm}
| |
| − | {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$
| |
| − |
| |
| − | *In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt:
| |
| − | :$$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$
| |
| − | *$x(t)$ und $X(f)$ haben unterschiedliche Einheiten, beispielsweise $x(t)$ in $\rm V$, $X(f)$ in $\rm V/Hz$.
| |
| − | *Der Zusammenhang zwischen diesem Modul und dem ähnlich aufgebauten Applet [[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang & Impulsantwort]] basiert auf dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Vertauschungssatz|Vertauschungssatz]].
| |
| − | *Alle Zeiten sind auf eine Zeit $T$ normiert und alle Frequenzen auf $1/T$ ⇒ die Spektralwerte $X(f)$ müssen noch mit der Normierungszeit $T$ multipliziert werden.
| |
| − |
| |
| − |
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel:}$ Stellt man einen Rechteckimpuls mit Amplitude $A_1 = 1$ und äquivalenter Impulsdauer $\Delta t_1 = 1$ ein, so ist $x_1(t)$ im Bereich $-0.5 < t < +0.5$ gleich Eins und außerhalb dieses Bereichs gleich Null. Die Spektralfunktion $X_1(f)$ verläuft $\rm si$–förmig mit $X_1(f= 0) = 1$ und der ersten Nullstelle bei $f=1$.
| |
| − |
| |
| − | *Soll mit dieser Einstellung ein Rechteckimpuls mit $A = K = 3 \ \rm V$ und $\Delta t = T = 2 \ \rm ms$ nachgebildet werden, dann sind alle Signalwerte mit $K = 3 \ \rm V$ und alle Spektralwerte mit $K \cdot T = 0.006 \ \rm V/Hz$ zu multiplizieren.
| |
| − | *Der maximale Spektralwert ist dann $X(f= 0) = 0.006 \ \rm V/Hz$ und die erste Nullstelle liegt bei $f=1/T = 0.5 \ \rm kHz$.}}
| |
| − |
| |
| − |
| |
| − | ===Gaußimpuls $\Rightarrow$ Gaussian Pulse ===
| |
| − |
| |
| − | *Die Zeitfunktion des Gaußimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
| |
| − | :$$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$
| |
| − | *Die äquivalente Zeitdauer $\Delta t$ ergibt sich aus dem flächengleichen Rechteck.
| |
| − | *Der Wert bei $t = \Delta t/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $t=0$.
| |
| − | *Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
| |
| − | :$$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$
| |
| − | *Je kleiner die äquivalente Zeitdauer $\Delta t$ ist, um so breiter und niedriger ist das Spektrum ⇒ [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Reziprozit.C3.A4tsgesetz_von_Zeitdauer_und_Bandbreite|Reziprozitätsgesetz von Bandbreite und Impulsdauer]].
| |
| − | *Sowohl $x(t)$ als auch $X(f)$ sind zu keinem $f$– bzw. $t$–Wert exakt gleich Null.
| |
| − | *Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $x(t)$ bereits bei $t=1.5 \Delta t$ auf weniger als $0.1\% $ des Maximums abgefallen.
| |
| − |
| |
| − |
| |
| − | ===Rechteckimpuls $\Rightarrow$ Rectangular Pulse ===
| |
| − | *Die Zeitfunktion des Rechteckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
| |
| − |
| |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
| |
| − |
| |
| − | *Der $\pm \Delta t/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
| |
| − | *Für die Spektralfunktion erhält man entsprechend den Gesetzmäßigkeiten der Fouriertransformation (1. Fourierintegral):
| |
| − | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{mit} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$
| |
| − | *Der Spektralwert bei $f=0$ ist gleich der Rechteckfläche der Zeitfunktion.
| |
| − | *Die Spektralfunktion besitzt Nullstellen in äquidistanten Abständen $1/\Delta t$.
| |
| − | *Das Integral über der Spektralfunktion $X(f)$ ist gleich dem Signalwert zum Zeitpunkt $t=0$, also der Impulshöhe $K$.
| |
| − |
| |
| − |
| |
| − | ===Dreieckimpuls $\Rightarrow$ Dreieckimpuls Triangular Pulse===
| |
| − | *Die Zeitfunktion des Dreieckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
| |
| − |
| |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
| |
| − |
| |
| − | *Die absolute Zeitdauer ist $2 \cdot \Delta t$; diese ist doppelt so groß als die des Rechtecks.
| |
| − | *Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
| |
| − | :$$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
| |
| − | *Obige Zeitfunktion ist gleich der Faltung zweier Rechteckimpulse, jeweils mit Breite $\Delta t$.
| |
| − | *Daraus folgt: $X(f)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion.
| |
| − | *$X(f)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf.
| |
| − | *Der asymptotische Abfall von $X(f)$ erfolgt hier mit $1/f^2$, während zum Vergleich der Rechteckimpuls mit $1/f$ abfällt.
| |
| − |
| |
| − |
| |
| − |
| |
| − | ===Trapezimpuls $\Rightarrow$ Trapezoidal Pulse ===
| |
| − | Die Zeitfunktion des Trapezimpulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:
| |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
| |
| − |
| |
| − | *Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
| |
| − | *Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:
| |
| − | :$$r=\frac{t_2-t_1}{t_2+t_1}.$$
| |
| − | *Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Dreieckimpuls.
| |
| − | *Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
| |
| − | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
| |
| − | *Der asymptotische Abfall von $X(f)$ liegt zwischen $1/f$ $($für Rechteck, $r=0)$ und $1/f^2$ $($für Dreieck, $r=1)$.
| |
| − |
| |
| | | | |
| − | ===Cosinus-Rolloff-Impuls $\Rightarrow$ Cosine-rolloff Pulse ===
| |
| − | Die Zeitfunktion des Cosinus-Rolloff-Impulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:
| |
| − |
| |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
| |
| − |
| |
| − | *Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
| |
| − | *Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:
| |
| − | :$$r=\frac{t_2-t_1}{t_2+t_1}.$$
| |
| − | *Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Cosinus-Quadrat-Impuls.
| |
| − | *Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
| |
| − | :$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
| |
| − | *Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $X(f)$ asymptotisch mit $f$ ab.
| |
| − |
| |
| − |
| |
| − | ===Cosinus-Quadrat-Impuls ===
| |
| − | *Dies ist ein Sonderfall des Cosinus-Rolloff-Impulses und ergibt sich für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$:
| |
| − |
| |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
| |
| − |
| |
| − | *Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
| |
| − | :$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
| |
| − | *Wegen der letzten ${\rm si}$-Funktion ist $X(f)=0$ für alle Vielfachen von $F=1/\Delta t$. Die äquidistanten Nulldurchgänge des Cos-Rolloff-Impulses bleiben erhalten.
| |
| − | *Aufgrund des Klammerausdrucks weist $X(f)$ nun weitere Nulldurchgänge bei $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... auf.
| |
| − | *Für die Frequenz $f=\pm F/2$ erhält man die Spektralwerte $K\cdot \Delta t/2$.
| |
| − | *Der asymptotische Abfall von $X(f)$ verläuft in diesem Sonderfall mit $1/f^3$.
| |
| | | | |
| | ==Versuchsdurchführung== | | ==Versuchsdurchführung== |
| Zeile 257: |
Zeile 143: |
| | *Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist. | | *Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist. |
| | | | |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(2)''' Vergleichen Sie den '''roten Gaußimpuls''' $(A_1 = 1, \Delta t_1 = 1)$ mit dem '''blauen Rechteckimpuls''' $(A_2 = 1,\Delta t_2)$.<br> Variieren Sie die äquivalente Impulsdauer $\Delta t_2$ zwischen $0.5$ und $2$. Interpretieren Sie die dargestellten Graphen.}}
| |
| − |
| |
| − | *Man erkennt das [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Reziprozit.C3.A4tsgesetz_von_Zeitdauer_und_Bandbreite|Reziprozitätsgesetz von Bandbreite und Impulsdauer]]. Je größer $\Delta t_2$ ist, um so höher und schmäler ist die Spektralfunktion $X_2(f)$.
| |
| − | *Bei jeder Einstellung von $\Delta t_2$ sind die Zeitsignalwerte $x_1(t= 0)$ und $x_2(t=0)$ gleich ⇒ Auch die Integrale über $X_1(f)$ und $X_2(f)$ sind identisch.
| |
| − |
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(3)''' Vergleichen Sie den '''roten Rechteckimpuls''' $(A_1 = 1, \Delta t_1 = 1)$ mit dem '''blauen Rechteckimpuls''' $(A_2 = 1,\Delta t_2 = 0.5)$.<br> Variieren Sie $\Delta t_2$ zwischen $0.05$ und $2$. Interpretieren Sie die dargestellten Graphen und extrapolieren Sie das Ergebnis.}}
| |
| − |
| |
| − | *Das blaue Spektrum ist nun doppelt so breit wie das rote, aber nur halb so hoch. Erste Nullstelle von $X_1(f)$ bei $f =1$ und von $X_2(f)$ erst bei $f =2$.
| |
| − | *Verkleinerung von $\Delta t_2$: $X_2(f)$ immer niedriger und breiter. Sehr flacher Verlauf bei $\Delta t_2 = 0.05$: $X_2(f = 0)= 0.05$, $X_2(f = \pm 3)= 0.048$.
| |
| − | *Würde man $\Delta t_2 = \varepsilon \to 0$ wählen (im Programm nicht möglich), so ergäbe sich das nahezu konstante, sehr kleine Spektrum $X_2(f)=A \cdot \varepsilon \to 0$.
| |
| − | *Erhöht man die Amplitude auf $A=1/\varepsilon$, so ergibt sich die konstante Spektralfunktion $X_2(f) = 1$ der [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals#Diracfunktion_im_Frequenzbereich|Diracfunktion]] $\delta(t)$. Das bedeutet:
| |
| − | * $\delta(t)$ ist durch ein Rechteck mit Breite $\Delta t = \varepsilon \to 0$ und Höhe $A = 1/\varepsilon \to \infty$ approximierbar. Das Diracgewicht ist Eins: $x(t) = 1 \cdot \delta (t)$.
| |
| − |
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(4)''' Vergleichen Sie den '''Rechteckimpuls''' $(A_1 = 1, \Delta t_1 = 1)$ mit dem '''Dreieckimpuls''' $(A_2 = 1,\Delta t_2 = 1)$. Interpretieren Sie die Spektalfunktionen.}}
| |
| − |
| |
| − | *Das (normierte) Spektrum des Rechtecks $x_1(t)$ mit den (normierte) Parametern $A_1 = 1, \ \Delta t_1 = 1$ lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
| |
| − | * Die Faltung des Rechtecks $x_1(t)$ mit sich selbst ergibt das Dreieck $x_2(t) = x_1(t) \star x_1(t)$. Nach dem [[Signaldarstellung/Faltungssatz_und_Faltungsoperation#Faltung_im_Zeitbereich|Faltungssatz]] gilt somit $X_2(f) = \big [X_1(f)\big]^2 $.
| |
| − | *Durch das Quadrieren der $\rm si$–förmigen Spektralfunktion $X_1(f)$ bleiben die Nullstellen in $X_2(f)$ erhalten. Es gilt aber nun $X_2(f) \ge 0$.
| |
| − |
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(5)''' Vergleichen Sie den '''Trapezimpuls''' $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem '''Dreieckimpuls''' $(A_2 = 1,\Delta t_2 = 1)$.<br> Variieren Sie $r_1$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_1(f)$.}}
| |
| − |
| |
| − | *Der Trapezimpuls mit Rolloff-Faktor $r_1= 0$ ist identisch mit dem Rechteckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
| |
| − | *Der Trapezimpuls mit Rolloff-Faktor $r_1= 1$ ist identisch mit dem Dreieckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}^2(\pi\cdot f)$.
| |
| − | *In beiden Fällen besitzt $X_1(f)$ äquidistante Nulldurchgänge bei $\pm 1$, $\pm 2$, ... (sonst keine). Mit $0 < r_1 < 1$ gibt es abhängig von $r_1$ weitere Nulldurchgänge.
| |
| − |
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(6)''' Vergleichen Sie den '''Trapezimpuls''' $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem '''Cosinus-Rolloff-Impuls''' $(A_2 = 1,\Delta t_2 = 1.0, r_1 = 0.5)$.<br> Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_2(f)$ für $r_2 = 0.7$.}}
| |
| − |
| |
| − | *Bei gleichem $r= 0.5$ besitzt der Cosinus-Rolloff-Impuls $X_2(f)$ ⇒ für $f > 1$ betragsmäßig größere Anteile als der Trapezimpuls.
| |
| − | *Bei gleichem Rolloff-Faktor $(r_1 = r_2= 0.5)$ verläuft der Abfall von $X_2(f)$ um die Frequenz $f = 0.5$ steiler als der Abfall von $X_1(f)$.
| |
| − | *Mit $r_1 = 0.5$ und $r_2 = 0.7$ gilt $x_1(t) \approx x_2(t)$ und damit auch $X_1(f) \approx X_2(f)$. Vergleichbare Flankensteilheit.
| |
| − |
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | '''(7)''' Vergleichen Sie den '''roten Trapezimpuls''' $(A_1 = 1, \Delta t_1 = 1, r_1 = 1)$ mit dem '''blauen Cosinus-Rolloff-Impuls''' $(A_2 = 1,\Delta t_2 = 1.0, r_2 = 1)$.<br> Interpretieren Sie die Zeitfunktion $x_2(t)$ und die Spektralfunktion $X_2(f)$ systemtheoretisch.}}
| |
| − |
| |
| − | *Es handelt sich bei $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \text{für} \ |t| \le 1$ um den Cosinus-Quadrat-Impuls. Nulldurchgänge bei $f = \pm 1$, $\pm 2$, ...
| |
| − | *Für die Frequenz $f=\pm 0.5$ erhält man die Spektralwerte $X_2(f)=0.5$. Der asymptotische Abfall verläuft hier mit $1/f^3$.
| |
| | | | |
| | | | |
| − | ==Zur Handhabung des Programms==
| |
| | <br> | | <br> |
| | [[Datei:Exercise_impuls.png |right|frame|Bildschirmabzug (englische Version, heller Hintergrund)]] | | [[Datei:Exercise_impuls.png |right|frame|Bildschirmabzug (englische Version, heller Hintergrund)]] |
Applet in neuem Tab öffnen
English Version
Programmbeschreibung
Dargestellt werden impulsförmige symmetrische Zeitsignale ⇒ „Impulse” $x(t)$ und die dazugehörigen Spektralfunktionen $X(f)$, nämlich
- Gaußimpuls (englisch: Gaussian pulse),
- Rechteckimpuls (englisch: Rectangular pulse),
- Dreieckimpuls (englisch: Triangular pulse),
- Trapezimpuls (englisch: Trapezoidal pulse),
- Cosinus–Rolloff–Impuls (englisch: Cosine-rolloff pulse).
Weiter ist zu beachten:
- Die Funktionen $x(t)$ bzw. $X(f)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
- Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
- Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $x(t)$ (Signalwerte) bzw. $X(f)$ (Spektralwerte) sind jeweils normiert.
Theoretischer Hintergrund
On–Off–Keying mit kohärenter Demodulation
Das einfachste digitale Modulationsverfahren ist On–Off–Keying $\rm (OOK)$. Dieses Verfahren wird teilweise auch als Amplitude Shift Keying $\rm (2–ASK)$ bezeichnet und kann im äquivalenten Tiefpassbereich wie folgt charakterisiert werden:
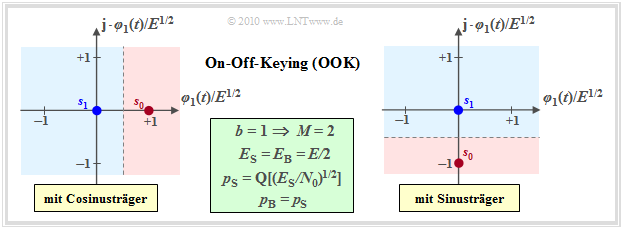
Signalraumkonstellationen für On–Off–Keying
$\rm OOK$ ist ein eindimensionales Modulationsverfahren mit $s_{1} \equiv 0$ und
- $s_{0} = \{E^{1/2}, 0\}$ (bei Cosinus–Träger) bzw.
- $s_{0} = \{0, -E^{1/2}\}$ (bei Sinus–Träger).
Bei kohärenter Demodulation ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht wieder aus den zwei Punkten $\boldsymbol{r}_0=\boldsymbol{s}_0$ und $\boldsymbol{r}_1=\boldsymbol{s}_1$.
Im kohärenten Fall ist das AWGN–Rauschen eindimensional mit der Varianz $\sigma_n^2 = N_0/2$ anzusetzen und man erhält entsprechend dem Theorieteil für die Bitfehlerwahrscheinlichkeit $p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s})$:
- $$p_{\rm B} = {\rm Q} \left ( \frac{d/2}{\sigma_n}\right ) = {\rm Q} \left ( \sqrt{\frac{E}{2 N_0}}\right )
= {\rm Q} \left ( \sqrt{{E_{\rm B}}/{N_0}}\right ) \hspace{0.05cm}.$$
- Diese Gleichung gilt für gleichwahrscheinliche Symbole und der Entscheiderschwelle $G$ in der Mitte zwischen $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.
- $E_{\rm B}=E/2$ bezeichnet für diesen Fall die „mittlere Energie pro Bit” und $N_0$ die (einseitige) AWGN–Rauschleistungsdichte.
- Die Funktion ${\rm Q}(x)$ nennt man das „Komplementäre Gaußsche Fehlerintegral”. Der Link weist auf das Applet Komplementäre Gaußsche Fehlerfunktionen.
On–Off–Keying mit inkohärenter Demodulation
Die zweite Grafik zeigt die Strukur des optimalen inkohärenten OOK–Empfängers (im äquivalenten Tiefpassbereich). Detailbeschreibung
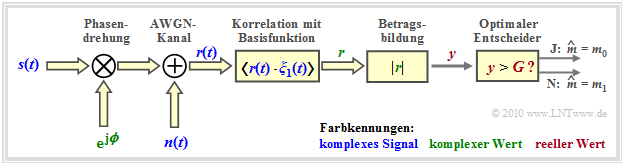
Empfänger für inkohärente OOK-Demodulation (komplexe Signale sind blau beschriftet)
Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex.
- Erforderlich ist nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}(t)$.
- Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$.
- Somit beträgt die mittlere Bitfehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen:
- $$p_{\rm B} = {\rm Pr}(\boldsymbol{r}\ne \boldsymbol{s}) = {1}/{ 2} \cdot {\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1})
+ {1}/{ 2} \cdot {\rm Pr}(\boldsymbol{r_1}|\boldsymbol{s_0}).$$
Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Rayleigh– und Riceverteilung
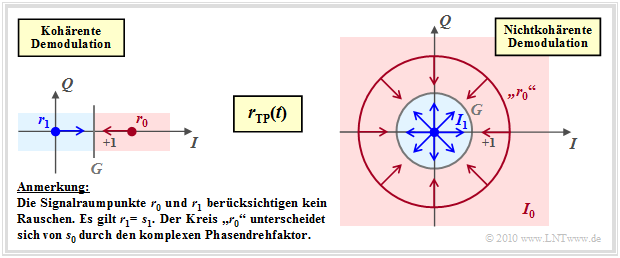
Zur Berechnung der Bitfehlerwahrscheinlichkeit bei inkohärenter Demodulation gehen wir von der rechten Skizze der nachfolgenden Grafik aus. Dargestellt ist das Empfangssignal im äquivalenten Tiefpassbereich in der komplexen Ebene.:
??? Kohärente und Inkohärente Demodulation von On-Off-Keying
- Der Punkt $\boldsymbol{s_1}=0$ führt im Empfangsignal zu $\boldsymbol{r_1}=0$.
- Dagegen wird aus dem Punkt $\boldsymbol{s_0}=1$ wegen des Phasenwinkels $\phi$ der Kreis $\boldsymbol{r_1}$ mit Radius $1$.
- Die Entscheidungsregion für die $1$ ist ebenfalls kreisförmig mit Radius $G$. Dies ist eine optimierbare Sytemgröße.
- Unter Berücksichtigung des AWGN–Rauschens gilt dann $\boldsymbol{r_1}=\boldsymbol{s_1} + \boldsymbol{n_1}$. Die Rauschkomponente $\boldsymbol{n_1}$ besitzt eine Rayleighverteilung $($Betrag der beiden mittelwertfreien Gaußkomponenten für $\rm I$ und $\rm Q)$. Damit erhält man:
- $${\rm Pr}(\boldsymbol{r_0}|\boldsymbol{s_1}) = \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1}) \,{\rm d} \eta
\hspace{0.05cm}.$$
- Mit der rotationssymmetrischen Rauschkomponente $\eta$ lautet die Rayleigh–WDF:
- $$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_1}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_1})=\frac{\eta}{\sigma^2}\cdot {\rm e}^{-\eta^2 / ( 2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sigma^2) } .$$
- Analog dazu gilt für die zweite bedingte Wahrscheinlichkeit in obiger Gleichung:
- $${\rm Pr}(\boldsymbol{r_1}|\boldsymbol{s_0}) = \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0}) \,{\rm d} \eta
\hspace{0.05cm},\hspace{0.3cm}\text{mit}$$
- $$p_{y\hspace{0.05cm}\vert \hspace{0.05cm}\boldsymbol{s_0}} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} \boldsymbol{s_0})=\frac{\eta}{\sigma^2}\cdot{\rm e}^{-({C^2+\it \eta^{\rm 2} })/ ({\rm 2 \it \sigma^{\rm 2} })}\cdot {\rm I_0}(\frac{\it \eta\cdot C}{\sigma^{\rm 2} }) \hspace{0.4cm}{\rm mit} \hspace{0.4cm} {\rm I_0}(\eta) = \sum_{k=0}^{\infty}\frac{(\eta/2)^{2k} }{k! \cdot {\rm \Gamma ({\it k}+1)} }.$$
Wir betrachten On–Off–Keying (bzw. 2–ASK) im äquivalenten Tiefpassbereich.
- Bei kohärenter Demodulation (linke Grafik) ist die Signalraumkonstellation des Empfangssignals gleich der des Sendesignals und besteht aus zwei Punkten.
- Die Entscheidungsgrenze $G$ liegt in der Mitte zwischen diesen Punkten $\boldsymbol{r}_0$ und $\boldsymbol{r}_1$.
- Die Pfeile markieren die grobe Richtung von Rauschvektoren, die eventuell zu Übertragungsfehlern führen.
Dagegen gilt bei nichtkohärenter Demodulation (rechte Grafik):
- Der Punkt $\boldsymbol{r}_1 = \boldsymbol{s}_1 = 0$ bleibt weiter erhalten. Dagegen kann $\boldsymbol{r}_0 = \boldsymbol{s}_0 \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi}$ auf jeden Punkt des Kreises um $\boldsymbol{s}_0$ liegen, da $\phi$ unbekannt ist.
- Der Entscheidungsprozess unter Berücksichtigung des AWGN–Rauschens ist nun zweidimensional zu interpretieren, wie durch die Pfeile in der rechten Grafik angedeutet.
- Das Entscheidungsgebiet $I_1$ ist ein Kreis, dessen Radius $G$ ein optimierbarer Parameter ist. Das Entscheidungsgebiet $I_0$ liegt außerhalb des Kreises.

Empfänger für nichtkohärente OOK-Demodulation (komplexen Signale sind blau beschriftet)
Damit liegt die Strukur des optimalen OOK–Empfängers (im äquivalenten Tiefpassbereich) fest. Entsprechend dieser zweiten Grafik gilt:
- Das Eingangssignal $\boldsymbol{r}(t) = \boldsymbol{s}(t) \cdot {\rm e}^{\hspace{0.02cm}{\rm j}\hspace{0.03cm}\phi} + \boldsymbol{n}(t)$ ist aufgrund des Phasenwinkels $\phi$ und wegen des komplexen Rauschterms $\boldsymbol{n}(t)$ im allgemeinen komplex. Erforderlich ist demzufolge nun die Korrelation zwischen dem komplexen Empfangssignal $\boldsymbol{r}(t)$ und einer komplexen Basisfunktion $\boldsymbol{\xi}_1(t)$.
- Das Ergebnis ist der (komplexe) Detektorwert $\boldsymbol{r}$, woraus als reelle Entscheidereingangsgröße der Betrag $y = |\boldsymbol{r}(t)|$ gebildet wird.
- Ist der Entscheidungswert $y \gt G$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. Somit beträgt die Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen:
- \[p_{\rm S} = {\rm Pr}({\cal{E}}) = {1}/{ 2} \cdot \int_{0}^{G} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}|\hspace{0.05cm} m_0) \,{\rm d} \eta
+ {1}/{ 2} \cdot \int_{G}^{\infty} p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (\eta \hspace{0.05cm}\vert \hspace{0.05cm} m_1) \,{\rm d} \eta
\hspace{0.05cm}.\]
- Aufgrund der Rice–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_0)$ und der Rayleigh–WDF $p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (\eta\hspace{0.05cm}|\hspace{0.05cm}m_1)$ kann allerdings diese Wahrscheinlichkeit nur numerisch ermittelt werden. Die optimale Entscheidungsgrenze $G$ ist vorher als die Lösung der folgenden Gleichung zu bestimmen:
- \[p_{y\hspace{0.05cm}\vert \hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_0) = p_{y\hspace{0.05cm}|\hspace{0.05cm}m} (G \hspace{0.05cm}|\hspace{0.05cm}m_1)
\hspace{0.05cm}.\]
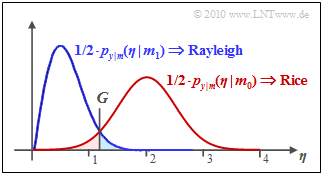
Dichtefunktionen für „OOK, nichtkohärent”
$\text{Beispiel 1:}$ Die Grafik zeigt das Ergebnis dieser Gleichung für $\sigma_n = 0.5$ und $C = 2$, wobei die (rote) Rice–WDF durch eine Gauß–WDF mit Mittelwert $C$ und Streuung $\sigma_n$ approximiert ist. Man erkennt daraus:
- Die optimale Entscheidungsgrenze $($hier: $G \approx 1.25)$ ergibt sich aus dem Schnittpunkt der beiden Kurven.
- Die Symbolfehlerwahrscheinlichkeit $p_{\rm S}$ ist die Summe der beiden farblich hinterlegten Flächen. Im Beispiel ergibt sich $p_{\rm S} \approx 5\%$.
Die Fehlerwahrscheinlichkeit für andere Werte von $C$ und $\sigma_n$ sowie die optimale Entscheidungsgrenze $G$ können Sie mit dem Berechnungstool Nichtkohärentes On–Off–Keying bestimmen.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart.
- „Rot” bezieht sich auf den ersten Parametersatz ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$.
- „Blau” bezieht sich auf den zweiten Parametersatz ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
- Werte betragsmäßig kleiner $0.0005$ werden im Programm zu Null gesetzt.
(1) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1, \Delta t_2 = 1)$ ⇒ Voreinstellung.
Welche Unterschiede erkennt man im Zeit- und im Frequenzbereich?
- Der Gaußimpuls reicht sowohl im Zeit– als auch im Frequenzbereich theoretisch bis ins Unendliche.
- Praktisch sind aber $x_1(t)$ für $|t| > 1.5$ und $X_1(f)$ für $|f| > 1.5$ nahezu Null.
- Das Rechteck ist zeitlich steng begrenzt: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ hat in einem viel größeren Bereich als $X_1(f)$ Anteile.
- Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist.
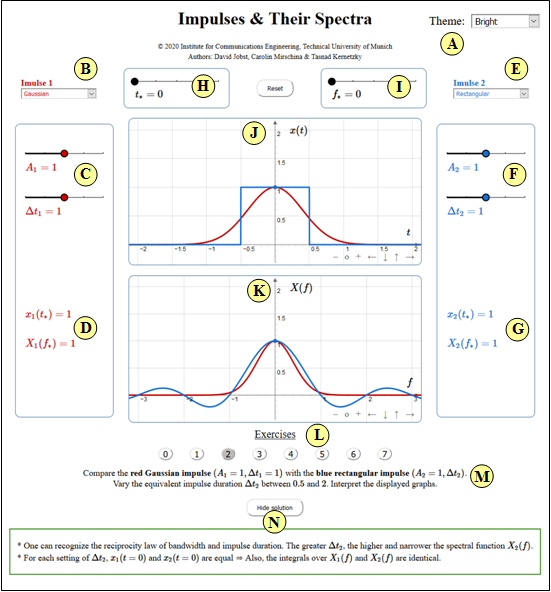
Bildschirmabzug (englische Version, heller Hintergrund)
(A) Theme (veränderbare grafische Oberflächengestaltung)
- Dark: schwarzer Hintergrund (wird von den Autoren empfohlen)
- Bright: weißer Hintergrund (empfohlen für Beamer und Ausdrucke)
- Deuteranopia: für Nutzer mit ausgeprägter Grün–Sehschwäche
- Protanopia: für Nutzer mit ausgeprägter Rot–Sehschwäche
(B) Vorauswahl für die Impulsform $x_1(t)$ (rote Kurve)
(C) Parameterfestlegung für $x_1(t)$
(D) Numerikausgabe für $x_1(t_*)$ und $X_1(f_*)$
(E) Vorauswahl für die Impulsform $x_2(t)$ (blaue Kurve)
(F) Parameterfestlegung für $x_2(t)$
(G) Numerikausgabe für $x_2(t_*)$ und $X_2(f_*)$
(H) Einstellung der Zeit $t_*$ für die Numerikausgabe
(I) Einstellung der Frequenz $f_*$ für die Numerikausgabe
(J) Bereich der graphischen Darstellung im Zeitbereich
(K) Bereich der graphischen Darstellung im Frequenzbereich
(L) Auswahl der Aufgabe entsprechend der Aufgabennummer
(M) Aufgabenbeschreibung und Fragestellung
(N) Musterlösung anzeigen und verbergen
Details zu den obigen Punkten (J ) und (K)
Zoom–Funktionen:
„$+$” (Vergrößern), „$-$” (Verkleinern), „$\rm o$” (Zurücksetzen)
Verschiebe–Funktionen: „$\leftarrow$” „$\uparrow$” „$\downarrow$” „$\rightarrow$”
„$\leftarrow$” bedeutet: Bildausschnitt nach links, Ordinate nach rechts
Andere Möglichkeiten:
- Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
- Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
- 2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.
- Letztmalige Überarbeitung 2020 durch Carolin Mirschina im Rahmen einer Werkstudententätigkeit.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Applet in neuem Tab öffnen
English Version





