Stochastische Signaltheorie/Erzeugung vorgegebener AKF-Eigenschaften: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==AKF am Ausgang eines nichtrekursiven Filters== | ==AKF am Ausgang eines nichtrekursiven Filters== | ||
| − | Wir betrachten ein ''nichtrekursives Laufzeitfilter M-ter Ordnung'' gemäß der folgenden Grafik. Die zeitdiskrete Eingangsgröße $〈x_ν〉$ ist | + | <br> |
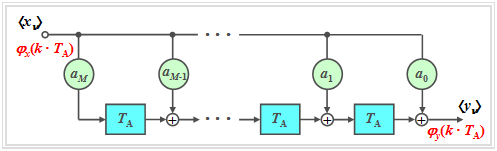
| + | Wir betrachten ein ''nichtrekursives Laufzeitfilter M-ter Ordnung'' gemäß der folgenden Grafik. | ||
| + | [[Datei:P_ID555__Sto_T_5_3_S1_neu.png |frame| Nichtrekursives Filter ''M''-ter Ordnung]] | ||
| + | Die zeitdiskrete Eingangsgröße $〈x_ν〉$ ist | ||
* mittelwertfrei ($m_x = 0$), | * mittelwertfrei ($m_x = 0$), | ||
*gaußverteilt (mit Streuung $σ_x$), und | *gaußverteilt (mit Streuung $σ_x$), und | ||
| − | * ohne Gedächtnis(„Weißes Rauschen”) | + | * ohne Gedächtnis („Weißes Rauschen”) <br>⇒ statistisch unabhängige Abtastwerte. |
| + | |||
| − | |||
Daraus ergeben sich folgende Eigenschaften: | Daraus ergeben sich folgende Eigenschaften: | ||
| Zeile 17: | Zeile 20: | ||
:$$\varphi _x ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\sigma _x ^2 } & {\rm{f\ddot{u}r}\quad {\it k} = 0,} \\ 0 & {\rm{f\ddot{u}r}\quad {\it k} \ne 0.} \\\end{array}} \right.$$ | :$$\varphi _x ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\sigma _x ^2 } & {\rm{f\ddot{u}r}\quad {\it k} = 0,} \\ 0 & {\rm{f\ddot{u}r}\quad {\it k} \ne 0.} \\\end{array}} \right.$$ | ||
*Die AKF der zeitdiskreten Ausgangsfolge $〈y_ν〉$ ist wie folgt gegeben: | *Die AKF der zeitdiskreten Ausgangsfolge $〈y_ν〉$ ist wie folgt gegeben: | ||
| − | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k } } \quad {\rm{f\ddot{u}r}}\quad {\it k} = 0, 1,\,...\,,\,{\it M}.$$ | + | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k } } \quad {\rm{f\ddot{u}r}}\quad {\it k} = 0, 1,\,\text{...}\,,\,{\it M}.$$ |
| − | *Alle AKF–Werte mit $k > M$ sind $0$, und alle AKF–Werte mit $k < M$ sind symmetrisch | + | *Alle AKF–Werte mit $k > M$ sind $0$, und alle AKF–Werte mit $k < M$ sind symmetrisch zu $k = 0$: |
:$$\varphi _y ( { - k \cdot T_{\rm A} } ) = \varphi _y ( {k \cdot T_{\rm A} } ).$$ | :$$\varphi _y ( { - k \cdot T_{\rm A} } ) = \varphi _y ( {k \cdot T_{\rm A} } ).$$ | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 1:}$ Liegt am Eingang eines nichtrekursiven Filters erster Ordnung (Filterkoeffizienten $a_0 = 0.6$, $a_1 = 0.8$) zeitdiskretes weißes Rauschen mit der Streuung $σ_x = 2$ an, so lauten die diskreten AKF-Werte des Ausgangssignals (alle anderen AKF-Werte sind $0$): | ||
[[Datei:P_ID597__Sto_T_5_3_S1_b_neu.png |frame| AKF am Ausgang eines Filters erster Ordnung|right]] | [[Datei:P_ID597__Sto_T_5_3_S1_b_neu.png |frame| AKF am Ausgang eines Filters erster Ordnung|right]] | ||
:$$\varphi _y (0) = \sigma _x ^2 \cdot ( {a_0 ^2 + a_1 ^2 }) = 4,$$ | :$$\varphi _y (0) = \sigma _x ^2 \cdot ( {a_0 ^2 + a_1 ^2 }) = 4,$$ | ||
:$$\varphi _y ( { - T_{\rm A} } ) = \varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot a_0 \cdot a_1 = 1.92.$$ | :$$\varphi _y ( { - T_{\rm A} } ) = \varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot a_0 \cdot a_1 = 1.92.$$ | ||
| + | <br clear=all> | ||
| + | Die Grafik kann wie folgt interpretiert werden: | ||
| + | *Wegen $a_0^2 + a_1^2 = 1$ besitzt das Ausgangssignal $y(t)$ genau die gleiche Varianz $σ_y^2 = φ_y(0)$ wie das Eingangssignal: $σ_x^2 = φ_x(0) = 4$. | ||
| + | *Im Gegensatz zur Eingangsfolge $〈x_ν〉$ gibt es bei der Ausgangsfolge $〈y_ν〉$ statistische Bindungen zwischen benachbarten Abtastwerten. }} | ||
| + | |||
| + | ==Zur Koeffizientenbestimmung== | ||
| + | <br> | ||
| + | Nun soll folgende Fragebeantwortet werden: | ||
| + | Wie können die Koeffizienten $a_0$, ... , $a_M$ eines nichtrekursiven Filters $M$–ter Ordnung ermittelt werden, | ||
| + | *wenn die gewünschten AKF-Werte $φ_y(0)$, ... , $φ_y(M · T_{\rm A})$ gegeben sind, und | ||
| + | * außerhalb des Bereiches von $-M · T_{\rm A}$ bis $+M · T_{\rm A}$ alle AKF-Werte Null sein sollen. | ||
| − | |||
| − | |||
| − | |||
| + | Für $σ_x = 1$ ergibt sich das folgende ''nichtlineare Gleichungssystem'', wobei zur Vereinfachung der Schreibweise $φ_k = φ_y(k · T_{\rm A})$ verwendet wird: | ||
| + | :$$\begin{align*}\varphi _0 & = \sum\limits_{\mu = 0}^M {a_\mu^2 ,}\\ \varphi _1 & = \sum\limits_{\mu = 0}^{M - 1} {a_\mu \cdot a_{\mu + 1} ,} \\ & . & \\ & . &\\ & . &\\ \varphi _{M - 1} & = a_0 \cdot a_{M - 1} + a_1 \cdot a_M , \\ \\ \varphi _M & = a_0 \cdot a_M .\end{align*}$$ | ||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Fazit:}$ | |
| − | Man erhält somit für die $M +$ | + | *Man erhält somit für die $M + 1$ Koeffizienten auch $M + 1$ unabhängige Gleichungen. |
| + | *Durch sukzessives Eliminieren der Koeffizienten $a_1$, ... , $a_M$ bleibt für $a_0$ schließlich eine nichtlineare Gleichung höherer Ordnung übrig.}} | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| − | *ein rekursives Filter erster Ordnung ⇒ $M = 1$, | + | $\text{Beispiel 2:}$ Wir betrachten die folgende Konstellation: |
| + | *ein rekursives Filter erster Ordnung ⇒ $M = 1$, | ||
*eine zeitdiskrete Eingangsfolge $〈x_ν〉$ mit Mittelwert $m_x =$ 0 und Streuung $σ_x = 1$, | *eine zeitdiskrete Eingangsfolge $〈x_ν〉$ mit Mittelwert $m_x =$ 0 und Streuung $σ_x = 1$, | ||
| − | *gewünschte AKF-Werte der Folge $〈y_ν〉: φ_y(0) = φ_0 =0.58$ und $φ_y(±T_{\rm A}) = φ_1 = 0.21$. | + | *gewünschte AKF-Werte der Folge $〈y_ν〉$: $ φ_y(0) = φ_0 =0.58$ und $φ_y(±T_{\rm A}) = φ_1 = 0.21$. |
| + | |||
Damit lautet das obige Gleichungssystem: | Damit lautet das obige Gleichungssystem: | ||
| Zeile 53: | Zeile 68: | ||
Dies führt zu einer Gleichung vom Grad $4$, nämlich | Dies führt zu einer Gleichung vom Grad $4$, nämlich | ||
:$$a_0 ^2 + \left( { { {0.21} }/{ {a_0 } } } \right)^2 = 0.58\quad \Rightarrow \quad a_0 ^4 - 0.58 \cdot a_0 ^2 + 0.21^2 = 0.$$ | :$$a_0 ^2 + \left( { { {0.21} }/{ {a_0 } } } \right)^2 = 0.58\quad \Rightarrow \quad a_0 ^4 - 0.58 \cdot a_0 ^2 + 0.21^2 = 0.$$ | ||
| − | Eine Lösung stellt $a_0 = 0.7$ dar. Durch Einsetzen in die zweite Gleichung findet man $a_1 = 0.3$. | + | Eine Lösung stellt $a_0 = 0.7$ dar. Durch Einsetzen in die zweite Gleichung findet man $a_1 = 0.3$. }} |
| − | Man erkennt aus diesem Beispiel, dass sich schon im einfachsten Fall ⇒ $M = 1$ | + | Man erkennt aus diesem Beispiel, dass sich schon im einfachsten Fall ⇒ $M = 1$ für $a_0$ eine nichtlineare Bestimmungsgleichung vom Grad $4$ ergibt. |
==Mehrdeutigkeiten bei der Koeffizientenbestimmung== | ==Mehrdeutigkeiten bei der Koeffizientenbestimmung== | ||
| + | <br> | ||
Wie das letzte Beispiel gezeigt hat, ist mit $M = 1$ die Bestimmungsgleichung für $a_0$ vom Grad $4$. Dies bedeutet gleichzeitig, dass es auch vier Koeffizientensätze gibt, die alle zur gleichen AKF führen. Dies ist aus folgenden Gründen einsichtig: | Wie das letzte Beispiel gezeigt hat, ist mit $M = 1$ die Bestimmungsgleichung für $a_0$ vom Grad $4$. Dies bedeutet gleichzeitig, dass es auch vier Koeffizientensätze gibt, die alle zur gleichen AKF führen. Dies ist aus folgenden Gründen einsichtig: | ||
*Die Koeffizienten $a_0$ und $a_1$ können gleichzeitig ihr Vorzeichen ändern, ohne dass dadurch das Gleichungssystem verändert wird. | *Die Koeffizienten $a_0$ und $a_1$ können gleichzeitig ihr Vorzeichen ändern, ohne dass dadurch das Gleichungssystem verändert wird. | ||
| Zeile 64: | Zeile 80: | ||
| − | {{Beispiel} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 3:}$ Wie im [[Stochastische_Signaltheorie/Erzeugung_vorgegebener_AKF-Eigenschaften#Zur_Koeffizientenbestimmung|letzten Abschnitt]] gezeigt wurde, ist der Parametersatz $a_0 = 0.7$, $a_1 = 0.3$ geeignet, die AKF-Werte $φ_0 = 0.58$ und $φ_1 = 0.21$ zu generieren. Die gewünschte AKF der Ausgangsfolge lautet dann in ausführlicher Schreibweise: | ||
:$$\varphi_y(\tau) = 0.58 \cdot \delta(\tau) + 0.21 \cdot \delta(\tau - T_{\rm A}) | :$$\varphi_y(\tau) = 0.58 \cdot \delta(\tau) + 0.21 \cdot \delta(\tau - T_{\rm A}) | ||
+ 0.21 \cdot \delta(\tau + T_{\rm A}) .$$ | + 0.21 \cdot \delta(\tau + T_{\rm A}) .$$ | ||
[[Datei:P_ID557__Sto_T_5_3_S2_b_neu_100.png |frame| Beispiel zur AKF-Berechnung|right]] | [[Datei:P_ID557__Sto_T_5_3_S2_b_neu_100.png |frame| Beispiel zur AKF-Berechnung|right]] | ||
| − | Zur gleichen AKF kommt man auch mit den | + | Zur gleichen AKF kommt man auch mit den Koeffizienten |
*$a_0 = - 0.7,\quad a_1 = -0.3,$ | *$a_0 = - 0.7,\quad a_1 = -0.3,$ | ||
*$a_0 = +0.3,\quad a_1 = +0.7,$ | *$a_0 = +0.3,\quad a_1 = +0.7,$ | ||
*$a_0 = - 0.3,\quad a_1 = -0.7.$ | *$a_0 = - 0.3,\quad a_1 = -0.7.$ | ||
| + | |||
Diese Konfigurationen ergeben sich durch | Diese Konfigurationen ergeben sich durch | ||
| − | *gleichzeitiges Multiplizieren aller Koeffizienten mit $ | + | *gleichzeitiges Multiplizieren aller Koeffizienten mit $-1$, sowie |
*Vertauschen der Zahlenwerte von $a_0$ und $a_1$. | *Vertauschen der Zahlenwerte von $a_0$ und $a_1$. | ||
| − | Die Grafik zeigt die entsprechenden Impulsantworten, die zur gewünschten AKF führen. | + | Die Grafik zeigt die entsprechenden Impulsantworten, die zur gewünschten AKF führen.}} |
| − | |||
| − | |||
| − | |||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:5.5 AKF-äquivalente Filter|Aufgabe 5.5: AKF-äquivalente Filter]] | ||
| − | + | [[Aufgaben:5.5Z AKF nach Filter 1. Ordnung|Aufgabe 5.5Z: AKF nach Filter 1. Ordnung]] | |
| − | |||
| − | [[Aufgaben:5.5Z AKF nach Filter 1. Ordnung| | ||
| − | [[Aufgaben:5.6 Filterdimensionierung|Aufgabe 5.6: | + | [[Aufgaben:5.6 Filterdimensionierung|Aufgabe 5.6: Filterdimensionierung]] |
| − | [[Aufgaben:5.6Z Nochmals FIlterdimensionierung| | + | [[Aufgaben:5.6Z Nochmals FIlterdimensionierung|Aufgabe 5.6Z: Nochmals FIlterdimensionierung]] |
{{Display}} | {{Display}} | ||
Version vom 13. April 2018, 15:57 Uhr
Inhaltsverzeichnis
AKF am Ausgang eines nichtrekursiven Filters
Wir betrachten ein nichtrekursives Laufzeitfilter M-ter Ordnung gemäß der folgenden Grafik.
Die zeitdiskrete Eingangsgröße $〈x_ν〉$ ist
- mittelwertfrei ($m_x = 0$),
- gaußverteilt (mit Streuung $σ_x$), und
- ohne Gedächtnis („Weißes Rauschen”)
⇒ statistisch unabhängige Abtastwerte.
Daraus ergeben sich folgende Eigenschaften:
- Die zeitdiskrete Autokorrelationsfunktion (AKF) am Eingang lautet:
- $$\varphi _x ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\sigma _x ^2 } & {\rm{f\ddot{u}r}\quad {\it k} = 0,} \\ 0 & {\rm{f\ddot{u}r}\quad {\it k} \ne 0.} \\\end{array}} \right.$$
- Die AKF der zeitdiskreten Ausgangsfolge $〈y_ν〉$ ist wie folgt gegeben:
- $$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k } } \quad {\rm{f\ddot{u}r}}\quad {\it k} = 0, 1,\,\text{...}\,,\,{\it M}.$$
- Alle AKF–Werte mit $k > M$ sind $0$, und alle AKF–Werte mit $k < M$ sind symmetrisch zu $k = 0$:
- $$\varphi _y ( { - k \cdot T_{\rm A} } ) = \varphi _y ( {k \cdot T_{\rm A} } ).$$
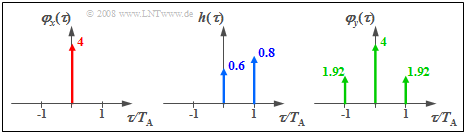
$\text{Beispiel 1:}$ Liegt am Eingang eines nichtrekursiven Filters erster Ordnung (Filterkoeffizienten $a_0 = 0.6$, $a_1 = 0.8$) zeitdiskretes weißes Rauschen mit der Streuung $σ_x = 2$ an, so lauten die diskreten AKF-Werte des Ausgangssignals (alle anderen AKF-Werte sind $0$):
- $$\varphi _y (0) = \sigma _x ^2 \cdot ( {a_0 ^2 + a_1 ^2 }) = 4,$$
- $$\varphi _y ( { - T_{\rm A} } ) = \varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot a_0 \cdot a_1 = 1.92.$$
Die Grafik kann wie folgt interpretiert werden:
- Wegen $a_0^2 + a_1^2 = 1$ besitzt das Ausgangssignal $y(t)$ genau die gleiche Varianz $σ_y^2 = φ_y(0)$ wie das Eingangssignal: $σ_x^2 = φ_x(0) = 4$.
- Im Gegensatz zur Eingangsfolge $〈x_ν〉$ gibt es bei der Ausgangsfolge $〈y_ν〉$ statistische Bindungen zwischen benachbarten Abtastwerten.
Zur Koeffizientenbestimmung
Nun soll folgende Fragebeantwortet werden:
Wie können die Koeffizienten $a_0$, ... , $a_M$ eines nichtrekursiven Filters $M$–ter Ordnung ermittelt werden,
- wenn die gewünschten AKF-Werte $φ_y(0)$, ... , $φ_y(M · T_{\rm A})$ gegeben sind, und
- außerhalb des Bereiches von $-M · T_{\rm A}$ bis $+M · T_{\rm A}$ alle AKF-Werte Null sein sollen.
Für $σ_x = 1$ ergibt sich das folgende nichtlineare Gleichungssystem, wobei zur Vereinfachung der Schreibweise $φ_k = φ_y(k · T_{\rm A})$ verwendet wird:
- $$\begin{align*}\varphi _0 & = \sum\limits_{\mu = 0}^M {a_\mu^2 ,}\\ \varphi _1 & = \sum\limits_{\mu = 0}^{M - 1} {a_\mu \cdot a_{\mu + 1} ,} \\ & . & \\ & . &\\ & . &\\ \varphi _{M - 1} & = a_0 \cdot a_{M - 1} + a_1 \cdot a_M , \\ \\ \varphi _M & = a_0 \cdot a_M .\end{align*}$$
$\text{Fazit:}$
- Man erhält somit für die $M + 1$ Koeffizienten auch $M + 1$ unabhängige Gleichungen.
- Durch sukzessives Eliminieren der Koeffizienten $a_1$, ... , $a_M$ bleibt für $a_0$ schließlich eine nichtlineare Gleichung höherer Ordnung übrig.
$\text{Beispiel 2:}$ Wir betrachten die folgende Konstellation:
- ein rekursives Filter erster Ordnung ⇒ $M = 1$,
- eine zeitdiskrete Eingangsfolge $〈x_ν〉$ mit Mittelwert $m_x =$ 0 und Streuung $σ_x = 1$,
- gewünschte AKF-Werte der Folge $〈y_ν〉$: $ φ_y(0) = φ_0 =0.58$ und $φ_y(±T_{\rm A}) = φ_1 = 0.21$.
Damit lautet das obige Gleichungssystem:
- $$\varphi _0 = a_0 ^2 + a_1 ^2 = 0.58,$$
- $$\varphi _1 = a_0 \cdot a_1 = 0.21.$$
Dies führt zu einer Gleichung vom Grad $4$, nämlich
- $$a_0 ^2 + \left( { { {0.21} }/{ {a_0 } } } \right)^2 = 0.58\quad \Rightarrow \quad a_0 ^4 - 0.58 \cdot a_0 ^2 + 0.21^2 = 0.$$
Eine Lösung stellt $a_0 = 0.7$ dar. Durch Einsetzen in die zweite Gleichung findet man $a_1 = 0.3$.
Man erkennt aus diesem Beispiel, dass sich schon im einfachsten Fall ⇒ $M = 1$ für $a_0$ eine nichtlineare Bestimmungsgleichung vom Grad $4$ ergibt.
Mehrdeutigkeiten bei der Koeffizientenbestimmung
Wie das letzte Beispiel gezeigt hat, ist mit $M = 1$ die Bestimmungsgleichung für $a_0$ vom Grad $4$. Dies bedeutet gleichzeitig, dass es auch vier Koeffizientensätze gibt, die alle zur gleichen AKF führen. Dies ist aus folgenden Gründen einsichtig:
- Die Koeffizienten $a_0$ und $a_1$ können gleichzeitig ihr Vorzeichen ändern, ohne dass dadurch das Gleichungssystem verändert wird.
- Ersetzt man $a_0$ durch $a_1$ und umgekehrt, so ergibt sich die gleiche Bestimmungsgleichung. Diese Operation entspricht einer Spiegelung und Verschiebung der Impulsantwort.
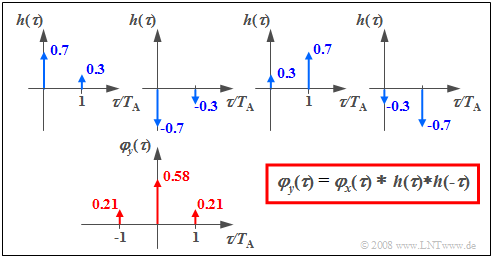
$\text{Beispiel 3:}$ Wie im letzten Abschnitt gezeigt wurde, ist der Parametersatz $a_0 = 0.7$, $a_1 = 0.3$ geeignet, die AKF-Werte $φ_0 = 0.58$ und $φ_1 = 0.21$ zu generieren. Die gewünschte AKF der Ausgangsfolge lautet dann in ausführlicher Schreibweise:
- $$\varphi_y(\tau) = 0.58 \cdot \delta(\tau) + 0.21 \cdot \delta(\tau - T_{\rm A}) + 0.21 \cdot \delta(\tau + T_{\rm A}) .$$
Zur gleichen AKF kommt man auch mit den Koeffizienten
- $a_0 = - 0.7,\quad a_1 = -0.3,$
- $a_0 = +0.3,\quad a_1 = +0.7,$
- $a_0 = - 0.3,\quad a_1 = -0.7.$
Diese Konfigurationen ergeben sich durch
- gleichzeitiges Multiplizieren aller Koeffizienten mit $-1$, sowie
- Vertauschen der Zahlenwerte von $a_0$ und $a_1$.
Die Grafik zeigt die entsprechenden Impulsantworten, die zur gewünschten AKF führen.
Aufgaben zum Kapitel
Aufgabe 5.5: AKF-äquivalente Filter
Aufgabe 5.5Z: AKF nach Filter 1. Ordnung
Aufgabe 5.6: Filterdimensionierung
Aufgabe 5.6Z: Nochmals FIlterdimensionierung