Aufgaben:Aufgabe 1.5: Nachbildung des Jakes–Spektrums: Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2124__Mob_A_1_5.png|right|frame]] | [[Datei:P_ID2124__Mob_A_1_5.png|right|frame]] | ||
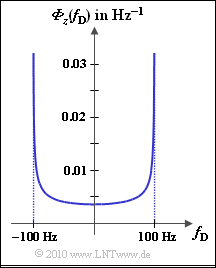
| − | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Dopplereffekt]] | + | Bei einem Mobilfunksystem macht sich der [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#Ph.C3.A4nomenologische_Beschreibung_des_Dopplereffekts|Dopplereffekt]] auch im Leistungsdichtespektrum der Dopplerfrequenz <i>f</i><sub>D</sub> bemerkbar. Es ergibt sich das sog. [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading|Jakes–Spektrum]], das für die maximale Dopplerfrequenz <i>f</i><sub>D, max</sub> = 100 Hz in der Grafik dargestellt ist. <i>Φ<sub>z</sub></i>(<i>f</i><sub>D</sub>) hat nur Anteile innerhalb des Bereichs ±<i>f</i><sub>D, max</sub>, wobei gilt: |
| + | :$${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus <i>Φ<sub>z</sub></i>(<i>f</i><sub>D</sub>) durch die [[Signaldarstellung/Fouriertransformation_und_-r%C3%BCcktransformation#Das_zweite_Fourierintegral|Fourierrücktransformation]]. | ||
| + | Mit der <i>Besselfunktion</i> erster Art und nullter Ordnung (J<sub>0</sub>) erhält man: | ||
| + | :$$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Modellierung_von_nichtfrequenzselektivem_Fading|Rayleigh–Kanalmodell]] zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang <i>H</i><sub>DF</sub>(<i>f</i><sub>D</sub>). Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. | ||
| + | Wir beschränken uns hier auf den Zweig zur Generierung des Realteils <i>x</i>(<i>t</i>). Für den Imaginärteil <i>y</i>(<i>t</i>) ergeben sich genau gleiche Verhältnisse. | ||
| + | Am Eingang des im [[Mobile_Kommunikation/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Frequenzselektives_Fading_vs._nichtfrequenzselektives_Fading|Rayleigh–Kanalmodell]] linken digitalen Filters liegt weißes Gaußsches Rauschen <i>n</i>(<i>t</i>) mit der Varianz <i>σ</i><sup>2</sup> = 0.5 an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu | ||
| + | :$$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''Hinweis:''' Die Aufgabe gehört zum [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh%E2%80%93Prozesses|Kapitel 1.3]] dieses Buches. Das digitale Filter wird in [[Stochastische_Signaltheorie/Digitale_Filter|Kapitel 5.2]] des Buches „Stochastische Signaltheorie” ausführlich behandelt. | ||
Version vom 21. Oktober 2017, 13:19 Uhr
Bei einem Mobilfunksystem macht sich der Dopplereffekt auch im Leistungsdichtespektrum der Dopplerfrequenz fD bemerkbar. Es ergibt sich das sog. Jakes–Spektrum, das für die maximale Dopplerfrequenz fD, max = 100 Hz in der Grafik dargestellt ist. Φz(fD) hat nur Anteile innerhalb des Bereichs ±fD, max, wobei gilt:
- $${\it \Phi}_z(f_{\rm D}) = \frac{2 \cdot \sigma^2}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.$$
Was im Frequenzbereich durch das Leistungsdichtespektrum ausgedrückt wird, beschreibt man im Zeitbereich durch die Autokorrelationsfunktion. Diese ergibt sich aus Φz(fD) durch die Fourierrücktransformation. Mit der Besselfunktion erster Art und nullter Ordnung (J0) erhält man:
- $$\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm}.$$
Um den Dopplereffekt – und damit eine Relativbewegung zwischen Sender und Empfänger – bei einer Systemsimulation zu berücksichtigen, werden im Rayleigh–Kanalmodell zwei digitale Filter eingefügt, jeweils mit dem Frequenzgang HDF(fD). Die Dimensionierung dieser Filter ist Inhalt dieser Aufgabe. Wir beschränken uns hier auf den Zweig zur Generierung des Realteils x(t). Für den Imaginärteil y(t) ergeben sich genau gleiche Verhältnisse. Am Eingang des im Rayleigh–Kanalmodell linken digitalen Filters liegt weißes Gaußsches Rauschen n(t) mit der Varianz σ2 = 0.5 an. Die Realteilkomponente ergibt sich dann gemäß der Faltung zu
- $$x(t) = n(t) \star h_{\rm DF}(t) \hspace{0.05cm}.$$
Hinweis: Die Aufgabe gehört zum Kapitel 1.3 dieses Buches. Das digitale Filter wird in Kapitel 5.2 des Buches „Stochastische Signaltheorie” ausführlich behandelt.
Fragebogen
Musterlösung