Applets:Zur Verdeutlichung der Pseudoternärcodes: Unterschied zwischen den Versionen
| Zeile 32: | Zeile 32: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | === Allgemeine Beschreibung der | + | === Allgemeine Beschreibung der Pseudoternärcodes === |
| − | Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die ''Ordnung'' des Codes. | + | Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die ''Ordnung'' des Codes. |
| + | |||
| + | [[Datei:P_ID1343__Dig_T_2_4_S1_v1.png|right|frame|Blockschaltbild und Ersatzschaltbild eines Pseudoternärcodierers|class=fit]] | ||
Typisch für eine symbolweise Codierung ist, dass | Typisch für eine symbolweise Codierung ist, dass | ||
| Zeile 40: | Zeile 42: | ||
*Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.<br><br> | *Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.<br><br> | ||
| − | Besondere Bedeutung besitzen | + | Besondere Bedeutung besitzen ''Pseudomehrstufencodes'' – besser bekannt unter der englischen Bezeichnung ''Partial Response Codes''. |
| − | + | ||
| − | Im Folgenden werden ausschließlich ''Pseudoternärcodes'' ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. | + | *Im Folgenden werden ausschließlich ''Pseudoternärcodes'' ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind. |
| + | *In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist. | ||
| − | |||
Man erkennt aus den beiden Darstellungen: | Man erkennt aus den beiden Darstellungen: | ||
| − | *Der | + | *Der Pseudoternärcodierer kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.<br> |
| − | *Der ''nichtlineare Vorcodierer'' gewinnt durch eine Modulo–2–Addition ( | + | *Der ''nichtlineare Vorcodierer'' gewinnt durch eine Modulo–2–Addition („Antivalenz”) zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind: |
:$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | :$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, | ||
+1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, | ||
+1\}\hspace{0.05cm}.$$ | +1\}\hspace{0.05cm}.$$ | ||
| − | *Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.<br> | + | *Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.<br> |
*Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das ''lineare Codiernetzwerk'' durch die herkömmliche Subtraktion | *Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das ''lineare Codiernetzwerk'' durch die herkömmliche Subtraktion | ||
| Zeile 59: | Zeile 61: | ||
C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$ | ||
| − | :das durch folgende [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] bezüglich dem Eingangssignal $b(t)$ und dem | + | :das durch folgende [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] bzw. [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|Übertragungsfunktion]] bezüglich dem Eingangssignal $b(t)$ und dem Ausgangssignal $c(t)$ beschrieben werden kann: |
:$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | :$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm | ||
C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$ | ||
| Zeile 67: | Zeile 69: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | Das $\text{Sendesignal aller Pseudoternärcodes}$ wird im Folgenden stets wie folgt dargestellt: |
:$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | Dieses ist sowohl ''ternär'' ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch ''redundant'' ⇒ statistische Bindungen zwischen den $a_\nu$.}} | + | Dieses ist sowohl ''ternär'' ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch ''redundant'' ⇒ statistische Bindungen zwischen den $a_\nu$. |
| + | Wird für den Sendegrundimpuls $g_s(t)$ das NRZ–Rechteck vorausgesetzt, so lautet das '''Sendesignal aller Pseudoternärcodes''':}} | ||
| + | |||
| + | |||
=== Eigenschaften des AMI-Codes=== | === Eigenschaften des AMI-Codes=== | ||
Version vom 28. Juli 2020, 13:42 Uhr
Inhaltsverzeichnis
Programmbeschreibung
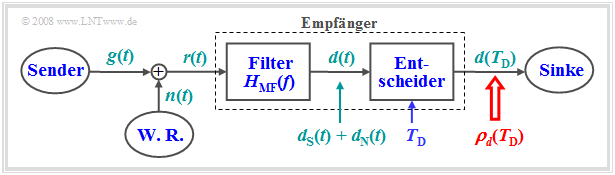
Das Applet soll die Eigenschaften des so genannten „Matched-Filters” $({\rm MF})$ verdeutlichen. Dieses dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude und/oder der Lage einer bekannten Signalform in einer stark verrauschten Umgebung. Oder allgemeiner gesprochen: Das Matched-Filter – manchmal auch als „Optimalfilter” oder als „Korrelationsfilter” bezeichnet – dient dem Nachweis der Signalexistenz.
Die Grafik zeigt den so genannten Matched-Filter-Empfänger:
- Dieser kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem Signal–zu–Rausch–Verhältnis $($englisch: signal–to–noise–ratio, $\rm SNR)$ – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht.
- Eine Anwendung ist die Radartechnik, bei der man zwar die Impulsform $g(t)$ kennt, nicht aber, wann der Impuls gesendet wurde und mit welcher Stärke und Verzögerung dieser ankommt.
- Das Matched-Filter wird aber auch als Empfangsfilter in digitalen Übertragungssystemen (oder zumindest als Teil davon) eingesetzt, um die Fehlerwahrscheinlichkeit des Systems zu minimieren.
Alle Parameter, Zeiten und Frequenzen sind als normierte Größen zu verstehen und damit dimensionslos.
- Für den Eingangsimpuls $g(t)$ sind „Rechteck”, „Gauß” und „Exponential” einstellbar, die jeweils durch die Impulsamplitude $A_g$, die äquivalente Impulsdauer $\Delta t_g$ sowie die Verschiebung $\tau_g$ gegenüber dem (hinsichtlich Zeit) symmetrischen Fall beschrieben werden. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Eingangsimpulsen.
- Für das Empfangsfilter kann zwischen den Alternativen „Spalt–Tiefpass”, „Gauß–Tiefpass”, „Tiefpass erster Ordnung”und „extrem akausales Filter” gewählt werden. Dargestellt werden die jeweiligen Impulsantworten $h(t)$, gekennzeichnet durch deren Höhe $A_h$, die äquivalente Dauer $\Delta t_h$ und die Verschiebung $\tau_h$. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Impulsantworten.
- Weitere Eingabeparameter sind der Detektionszeitpunkt $T_{\rm D}$ sowie die ebenfalls normierte Rauschleistungsdichte $N_0$ am Empfängereingang.
Als Numerikwerte ausgegeben werden
- die Energie $E_g$ des Eingangsimpulses $g(t)$, der Nutzabtastwert $d_{\rm S} (T_{\rm D})$ am Filterausgang sowie die Rauschvarianz $\sigma_d^2$ am Filterausgang,
- das Signal–zu–Rausch–Verhältnis $\rm (SNR)$ $\rho_{d} (T_{\rm D})$ am Filterausgang und die zugehörige dB–Angabe $10 \cdot \lg \ \rho_{d} (T_{\rm D})$,
- der hierfür maximale Wert $10 \cdot \lg \ \rho_{\rm MF}$.
Erfüllt die eingegebene Konfiguration die Matched-Filter-Bedingungen, dann gilt: $10 \cdot \lg \ \rho_{d} (T_{\rm D,\ opt}) = 10 \cdot \lg \ \rho_{\rm MF}$.
Theoretischer Hintergrund
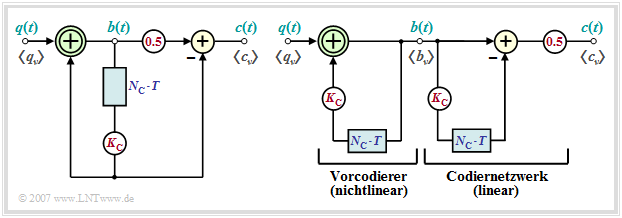
Allgemeine Beschreibung der Pseudoternärcodes
Bei der symbolweisen Codierung wird mit jedem ankommenden Quellensymbol $q_\nu$ ein Codesymbol $c_\nu$ erzeugt, das außer vom aktuellen Eingangssymbol $q_\nu$ auch von den $N_{\rm C}$ vorangegangenen Symbolen $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $ abhängt. $N_{\rm C}$ bezeichnet man als die Ordnung des Codes.
Typisch für eine symbolweise Codierung ist, dass
- die Symboldauer $T$ des Codersignals (und des Sendesignals) mit der Bitdauer $T_{\rm B}$ des binären Quellensignals übereinstimmt, und
- Codierung und Decodierung nicht zu größeren Zeitverzögerungen führen, die bei Verwendung von Blockcodes unvermeidbar sind.
Besondere Bedeutung besitzen Pseudomehrstufencodes – besser bekannt unter der englischen Bezeichnung Partial Response Codes.
- Im Folgenden werden ausschließlich Pseudoternärcodes ⇒ Stufenzahl $M = 3$ betrachtet, die durch das Blockschaltbild entsprechend der linken Grafik beschreibbar sind.
- In der rechten Grafik ist ein Ersatzschaltbild angegeben, das für eine Analyse dieser Codes sehr gut geeignet ist.
Man erkennt aus den beiden Darstellungen:
- Der Pseudoternärcodierer kann in den nichtlinearen Vorcodierer und ein lineares Codiernetzwerk aufgespalten werden, wenn man – wie im rechten Ersatzschaltbild dargestellt – die Verzögerung um $N_{\rm C} \cdot T$ und die Gewichtung mit $K_{\rm C}$ zur Verdeutlichung zweimal zeichnet.
- Der nichtlineare Vorcodierer gewinnt durch eine Modulo–2–Addition („Antivalenz”) zwischen den Symbolen $q_\nu$ und $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $ die vorcodierten Symbole $b_\nu$, die ebenfalls binär sind:
- $$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.$$
- Die Symbole $b_\nu$ sind wie die Quellensymbole $q_\nu$ statistisch voneinander unabhängig. Der Vorcodierer fügt also keine Redundanz hinzu. Er gestattet aber eine einfachere Realisierung des Decoders und verhindert eine Fehlerfortpflanzung nach einem Übertragungsfehler.
- Die eigentliche Umcodierung von binär $(M_q = 2)$ auf ternär $(M = M_c = 3)$ bewirkt das lineare Codiernetzwerk durch die herkömmliche Subtraktion
- $$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$
- das durch folgende Impulsantwort bzw. Übertragungsfunktion bezüglich dem Eingangssignal $b(t)$ und dem Ausgangssignal $c(t)$ beschrieben werden kann:
- $$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$
- Die relative Coderedundanz ist für alle Pseudoternärcodes gleich. Setzt man in die allgemeine Definitionsgleichung $M_q=2$, $M_c=3$ und $T_c =T_q$ ein, so erhält man
- $$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$
Das $\text{Sendesignal aller Pseudoternärcodes}$ wird im Folgenden stets wie folgt dargestellt:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T)\hspace{0.05cm}.$$
Dieses ist sowohl ternär ⇒ $a_\nu \in \{-1, \ 0, +1\}$ als auch redundant ⇒ statistische Bindungen zwischen den $a_\nu$. Wird für den Sendegrundimpuls $g_s(t)$ das NRZ–Rechteck vorausgesetzt, so lautet das Sendesignal aller Pseudoternärcodes:
Eigenschaften des AMI-Codes
Die einzelnen Pseudoternärcodes unterscheiden sich in den Parametern $N_{\rm C}$ und $K_{\rm C}$.
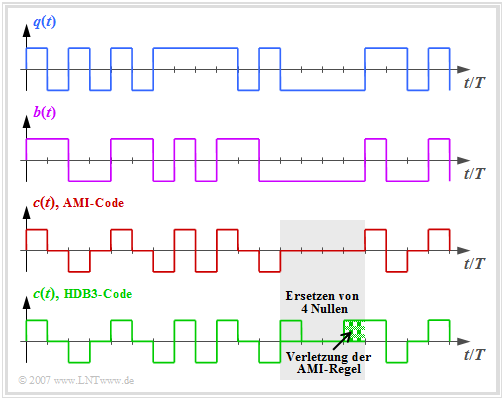
Der bekannteste Vertreter ist der Bipolarcode erster Ordnung mit den Codeparametern $N_{\rm C} = 1$ und $K_{\rm C} = 1$, der auch unter der Bezeichnung AMI–Code (von: Alternate Mark Inversion) bekannt ist. Dieser wird zum Beispiel bei ISDN (Integrated Services Digital Networks) auf der so genannten $S_0$–Schnittstelle eingesetzt.
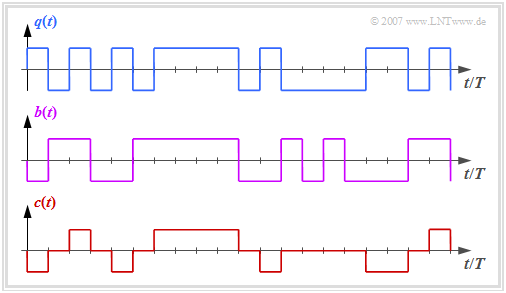
Die Grafik zeigt oben das binäre Quellensignal $q(t)$. Im zweiten und dritten Diagramm sind dargestellt:
- das ebenfalls binäre Signal $b(t)$ nach dem Vorcodierer, und
- das Codersignal $c(t) = s(t)$ des AMI–Codes.
Man erkennt das einfache AMI–Codierprinzip:
- Jeder Binärwert „–1” von $q(t)$ ⇒ Symbol $\rm L$ wird durch den ternären Amplitudenkoeffizienten $a_\nu = 0$ codiert.
- Der Binärwert „+1” von $q(t)$ ⇒ Symbol $\rm H$ wird alternierend mit $a_\nu = +1$ und $a_\nu = -1$ dargestellt.
Damit wird sichergestellt, dass im AMI–codierten Signal keine langen „+1”– bzw. „–1”–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde.
Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird.
Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der B6ZS–Code und der HDB3–Code:
- Beim HDB3–Code (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.
- Im grau hinterlegten Bereich ist dies die Folge „+ 0 0 +”, da das letzte Symbol vor der Ersetzung ein „Minus” war.
- Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf $3$ begrenzt und beim B6ZS–Code auf $5$.
- Der Decoder erkennt diese Codeverletzung und ersetzt „+ 0 0 +” wieder durch „0 0 0 0”.
Leistungsdichtespektrum des AMI-Codes
Der Frequenzgang des linearen Codiernetzwerks eines Pseudoternärcodes lautet allgemein:
- $$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi\hspace{0.03cm}\cdot \hspace{0.03cm}f \hspace{0.03cm}\cdot \hspace{0.03cm} N_{\rm C}\hspace{0.03cm}\cdot \hspace{0.03cm}T} \big] ={1}/{2} \cdot \big [1 - K \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} \alpha} \big ]\hspace{0.05cm}.$$
Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten $(K$ und $\alpha$ sind Abkürzungen entsprechend obiger Gleichung$)$:
- $$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos (\alpha) \big ] $$
- $$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ] \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$
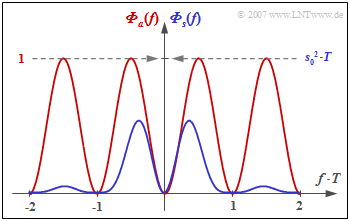
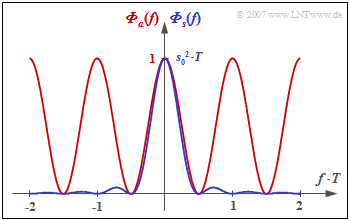
Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$:
- $${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$$
Die Grafik zeigt
- das LDS ${\it \Phi}_a(f)$ der Amplitudenkoeffizienten (rote Kurve), und
- das LDS ${\it \Phi}_s(f)$ des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.
Man erkennt aus dieser Darstellung
- die Gleichsignalfreiheit des AMI–Codes, da ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$ ist,
- die Leistung $P_{\rm S} = s_0^2/2$ des AMI–codierten Sendesignals (Integral über ${\it \Phi}_s(f)$ von $- \infty$ bis $+\infty$).
Hinweise:
- Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.
- Die hier behandelte Thematik können Sie sich mit dem interaktiven Applet Signale, AKF und LDS der Pseudoternärcodes verdeutlichen.
Eigenschaften des Duobinärcodes
Der Duobinärcode ist durch die Codeparameter $N_{\rm C} = 1$ und $K_{\rm C} = -1$ festgelegt. Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten bzw. für das LDS des Sendesignals:
- $${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm},$$
- $$ {\it \Phi}_s(f) = s_0^2 \cdot T \cdot \cos^2 (\pi f T)\cdot {\rm si}^2 (\pi f T)= s_0^2 \cdot T \cdot {\rm si}^2 (2 \pi f T) \hspace{0.05cm}.$$
Die Grafik zeigt das Leistungsdichtespektrum
- der Amplitudenkoeffizienten ⇒ ${\it \Phi}_a(f)$ als rote Kurve,
- des gesamten Sendsignals ⇒ ${\it \Phi}_s(f)$ als blaue Kurve.
In der zweiten Grafik sind die Signale $q(t)$, $b(t)$ und $c(t) = s(t)$ skizziert. Wir verweisen hier wieder auf das Applet Signale, AKF und LDS der Pseudoternärcodes, das auch die Eigenschaften des Duobinärcodes verdeutlicht.
Aus diesen Darstellungen geht hervor:
- Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität („+1” bzw. „–1”) direkt aufeinanderfolgen.
- Deshalb gilt ${\it \Phi}_a(f = 0)=1$ und ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.
- Dagegen tritt beim Duobinärcode die alternierende Folge „ ... , +1, –1, +1, –1, +1, ... ” nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
- Deshalb gilt beim Duobinärcode: ${\it \Phi}_s(f = 1/(2T) = 0$.
- Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ des pseudoternären Duobinärcodes ist identisch mit dem LDS bei redundanzfreier Binärcodierung mit halber Rate $($Symboldauer $2T)$.
AKF–Berechnung eines Digitalsignals
Zur Vereinfachung der Schreibweise wird im Folgenden $M_c = M$ und $T_c = T$ gesetzt. Damit kann für das Sendesignal $s(t)$ bei einer zeitlich unbegrenzten Nachrichtenfolge mit $a_\nu \in \{ a_1,$ ... , $a_M\}$ geschrieben werden:
- $$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$$
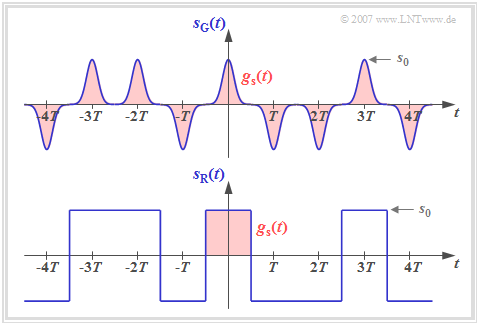
Diese Signaldarstellung beinhaltet sowohl die Quellenstatistik $($Amplitudenkoeffizienten $a_\nu$) als auch die Sendeimpulsform $g_s(t)$. Die Grafik zeigt zwei binäre bipolare Sendesignale $s_{\rm G}(t)$ und $s_{\rm R}(t)$ mit gleichen Amplitudenkoeffizienten $a_\nu$, die sich somit lediglich durch den Sendegrundimpuls $g_s(t)$ unterscheiden.
Man erkennt aus dieser Darstellung, dass ein Digitalsignal im Allgemeinen nichtstationär ist:
- Beim Sendesignal $s_{\rm G}(t)$ mit schmalen Gaußimpulsen ist die Nichtstationarität offensichtlich, da zum Beispiel bei Vielfachen von $T$ die Varianz $\sigma_s^2 = s_0^2$ ist, während genau dazwischen $\sigma_s^2 \approx 0$ gilt.
- Auch das Signal $s_{\rm R}(t)$ mit NRZ–rechteckförmigen Impulsen ist im strengen Sinne nichtstationär, da sich hier die Momente an den Bitgrenzen gegenüber allen anderen Zeitpunkten unterscheiden. Beispielsweise gilt $s_{\rm R}(t = \pm T/2)=0$.
$\text{Definition:}$ Einen Zufallsprozess, dessen Momente $m_k(t) = m_k(t+ \nu \cdot T)$ sich periodisch mit $T$ wiederholen, bezeichnet man als zyklostationär; $k$ und $\nu$ besitzen bei dieser impliziten Definition ganzzahlige Zahlenwerte.
Viele der für ergodische Prozesse gültigen Regeln kann man mit nur geringen Einschränkungen auch auf zykloergodische (und damit auf zyklostationäre ) Prozesse anwenden.
Insbesondere gilt für die Autokorrelationsfunktion (AKF) solcher Zufallsprozesse mit Mustersignal $s(t)$:
- $$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] \hspace{0.05cm}.$$
Mit obiger Gleichung des Sendesignals kann die AKF als Zeitmittelwert auch wie folgt geschrieben werden:
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T} \cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -N}^{+N} a_\nu \cdot a_{\nu + \lambda} \cdot \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau - \lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.$$
Da die Grenzwert–, Integral– und Summenbildung miteinander vertauscht werden darf, kann mit den Substitutionen $N = T_{\rm M}/(2T)$, $\lambda = \kappa- \nu$ und $t - \nu \cdot T \to T$ hierfür auch geschrieben werden:
- $$\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}} \cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} \sum_{\nu = -\infty}^{+\infty} \sum_{\kappa = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T ) \cdot a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T ) \,{\rm d} t \hspace{0.05cm}.$$
Nun werden zur Abkürzung folgende Größen eingeführt:
$\text{Definition:}$ Die diskrete AKF der Amplitudenkoeffizienten liefert Aussagen über die linearen statistischen Bindungen der Amplitudenkoeffizienten $a_{\nu}$ und $a_{\nu + \lambda}$ und besitzt keine Einheit:
- $$\varphi_a(\lambda) = \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot a_{\nu + \lambda} \hspace{0.05cm}.$$
$\text{Definition:}$ Die Energie–AKF des Grundimpulses ist ähnlich definiert wie die allgemeine (Leistungs–)AKF. Sie wird mit einem Punkt gekennzeichnet. Da $g_s(t)$ energiebegrenzt ist, kann auf die Division durch $T_{\rm M}$ und den Grenzübergang verzichtet werden:
- $$\varphi^{^{\bullet} }_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$$
$\text{Definition:}$ Für die Autokorrelationsfunktion eines Digitalsignals $s(t)$ gilt allgemein:
- $$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
Das Signal $s(t)$ kann dabei binär oder mehrstufig, unipolar oder bipolar sowie redundanzfrei oder redundant (leitungscodiert) sein. Die Impulsform wird durch die Energie–AKF berücksichtigt.
Beschreibt das Digitalsignal $s(t)$ einen Spannungsverlauf, so hat die Energie–AKF des Grundimpulses $g_s(t)$ die Einheit $\rm V^2s$ und $\varphi_s(\tau)$ die Einheit $\rm V^2$, jeweils bezogen auf den Widerstand $1 \ \rm \Omega$.
Anmerkung: Im strengen Sinne der Systemtheorie müsste man die AKF der Amplitudenkoeffizienten wie folgt definieren:
- $$\varphi_{a , \hspace{0.08cm}\delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty} \varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
Damit würde sich die obige Gleichung wie folgt darstellen:
- $$\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a , \hspace{0.08cm} \delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$
Zur einfacheren Darstellung wird im Folgenden die diskrete AKF der Amplitudenkoeffizienten
⇒ $\varphi_a(\lambda)$
ohne diese Diracfunktionen geschrieben.
LDS–Berechnung eines Digitalsignals
Die Entsprechungsgröße zur Autokorrelationsfunktion (AKF) eines Zufallssignals ⇒ $\varphi_s(\tau)$ ist im Frequenzbereich das Leistungsdichtespektrum (LDS) ⇒ ${\it \Phi}_s(f)$, das mit der AKF über das Fourierintegral in einem festen Bezug steht:
- $$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$$
Berücksichtigt man den Zusammenhang zwischen Energie–AKF und Energiespektrum,
- $$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm},$$
sowie den Verschiebungssatz, so kann das Leistungsdichtespektrum des Digitalsignals $s(t)$ in folgender Weise dargestellt werden:
- $${\it \Phi}_s(f) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it \Phi}^{^{\hspace{0.05cm}\bullet}}_{gs}(f) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = {1}/{T} \cdot |G_s(f)|^2 \cdot \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( 2 \pi f \lambda T)\hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass ${\it \Phi}_s(f)$ und $|G_s(f)|^2$ reellwertig sind und gleichzeitig $\varphi_a(-\lambda) =\varphi_a(+\lambda)$ gilt.
Definiert man nun die spektrale Leistungsdichte der Amplitudenkoeffizienten zu
- $${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm},$$
so erhält man den folgenden Ausdruck:
- $${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$$
$\text{Fazit:}$ Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ eines Digitalsignals $s(t)$ kann als Produkt zweier Funktionen dargestellt werden::
- Der erste Term ${\it \Phi}_a(f)$ ist dimensionslos und beschreibt die spektrale Formung des Sendesignals durch die statistischen Bindungen der Quelle.
- Dagegen berücksichtigt $\vert G_s(f) \vert^2$ die spektrale Formung durch den Sendegrundimpuls $g_s(t)$. Je schmaler dieser ist, desto breiter ist $\vert G_s(f) \vert^2$ und um so größer ist damit der Bandbreitenbedarf.
- Das Energiespektrum hat die Einheit $\rm V^2s/Hz$ und das Leistungsdichtespektrum – aufgrund der Division durch den Symbolabstand $T$ – die Einheit $\rm V^2/Hz$. Beide Angaben gelten wieder nur für den Widerstand $1 \ \rm \Omega$.
Fehlerwahrscheinlichkeit der Pseudoternärcodes
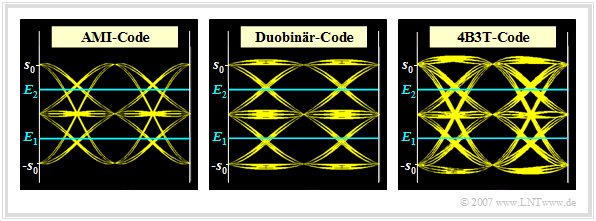
Die Grafik zeigt die Augendiagramme (ohne Rauschen) bei Verwendung
- von AMI–Code (links)
- und Duobinärcode (Mitte)
- im Vergleich zum 4B3T–Code (rechts).
Es gelten die gleichen Voraussetzungen wie auf der Seite Fehlerwahrscheinlichkeit der 4B3T-Codes. Insbesondere:
- Cosinus–Rolloff–Charakteristik des Gesamtfrequenzgangs (von Sender und Empfänger) mit dem Rolloff–Faktor $r = 0.8$.
Die Ergebnisse sind wie folgt zu interpretieren:
- Man erkennt in der linken Grafik, dass beim AMI–Code die horizontalen Linien bei $+s_0$ und $-s_0$ fehlen (Gleichsignalfreiheit!), während beim Duobinärcode (mittlere Grafik) keine Übergänge von $+s_0$ auf $-s_0$ (und umgekehrt) möglich sind. Beim 4B3T–Code erkennt man im Augendiagramm deutlich mehr Linien als bei den beiden linken Bildern. Der redundanzfreie Ternärcode würde nahezu das gleiche Ergebnis liefern.
- Auf der oben zitierten Seite wurde die Symbolfehlerwahrscheinlichkeit des 4B3T–Codes für die Leistungskenngröße $10 \cdot \lg \hspace{0.05cm}(s_0^2 \cdot T/N_0) = 13 \ \rm dB$ (gültig für Spitzenwertbegrenzung!) wie folgt berechnet:
- $${ \sigma_d}/{s_0} = 0.145 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( \frac{s_0/2}{ \sigma_d} \right) \approx {4}/{3} \cdot {\rm Q} \left( 3.45 \right) = 3.7 \cdot 10^{-4} \hspace{0.05cm}.$$
- Bei Verwendung eines Pseudoternärcodes ergibt sich eine größere Fehlerwahrscheinlichkeit, weil hier der Rauscheffektivwert gegenüber der redundanzfreien Binärcodierung nicht verringert wird:
- $${ \sigma_d}/{s_0} = 0.167 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( \frac{s_0/2}{ \sigma_d} \right) \approx {4}/{3} \cdot {\rm Q} \left( 3 \right) = 1.8 \cdot 10^{-3} \hspace{0.05cm}.$$
- Bei Erfüllung der Nyquistbedingung unterscheiden sich der AMI– und der Duobinärcode trotz völlig unterschiedlicher Augendiagramme hinsichtlich der Fehlerwahrscheinlichkeit nicht.
- Wie aber im Abschnitt Augenöffnung bei den Pseudoternärcodes noch gezeigt werden wird, ist das Fehlerverhalten der beiden Codes immer dann extrem unterschiedlich, wenn Impulsinterferenzen eine Rolle spielen.
===Detailbeschreibung des zugrunde liegenden Modells===
Für die einzelnen Komponenten des obigen Blockschaltbild gelten folgende Voraussetzungen:
- Der Nutzanteil $g(t)$ des Empfangssignals $r(t)=g(t)+n(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $ [g(t) ]^2$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
- Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
- Das Filterausgangssignal $d(t)= d_{\rm S}(t) + d_{\rm N}(t)$ besteht additiv aus zwei Anteilen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S\hspace{0.04cm}$ignal $g(t)$ zurück, $d_{\rm N}(t)$ auf das $\rm N\hspace{0.04cm}$oise $n(t)$.
- Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma_d^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Hierbei bezeichnen ${σ_d}^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) Detektionszeitpunkt.
Matched-Filter-Optimierung
Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit Impulsantwort $h(t)$ und Frequenzgang $H(f) =\mathcal{ F}\{h(t)\}$ geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm S$ für „Signal”):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
Damit lautet das hier vorliegende Optimierungsproblem:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
Dieser Quotient wird für den folgenden Frequenzgang $H(f)$ am größten wird:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } } \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \rho _{\rm MF}.$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Herleitung des Matched–Filter–Kriteriums:}$
$(1)$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
$(2)$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
$(3)$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ ergibt sich somit die folgende Schranke:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
$(4)$ Wir setzen für den Filterfrequenzgang nun versuchsweise ein:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$
$(5)$ Dann erhält man aus der obigen Gleichung $(2)$ folgendes Ergebnis:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
$\text{Das heißt:}$
- Mit dem Ansatz $(4)$ für das Matched–Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht.
- Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen.
- Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.
$\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit Amplitude $\rm 1\hspace{0.05cm}V$, Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden.
- Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
- Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
Das beste Ergebnis ⇒ das maximale S/N–Verhältnis erzielt man mit dem Matched-Filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}= 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{\rm MF}.$$
Interpretation des Matched-Filters
Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
Diese beiden Funktionen lassen sich wie folgt interpretieren:
- Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
- Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig.
- Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
- Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
- Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)\equiv 0$ $($„Kausalität”, siehe Buch Lineare zeitinvariante Systeme$)$.
- Der Nutzanteil $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der Energie-AKF $\varphi^{^{\bullet} }_{g} (t )$ und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Bitte beachten Sie:}$ Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.
$\text{Beispiel 2:}$ Wir gehen davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.08cm}ms$ und $\rm 2.5\hspace{0.08cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ gewünscht wird.
Unter diesen Voraussetzungen gilt:
- Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ bis $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$ konstant sein.
- Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
- Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier $\rm si$–förmig.
- Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.
Weitere Angaben zu den betrachteten Eingangsimpulsen
Alle Angaben sind ohne Berücksichtigung der Verzögerung $\tau_g$.
(1) Rechteckimpuls ⇒ Rectangular Impulse
- Der Impuls $g(t)$ hat im Bereich $\pm \Delta t_g/2$ die konstante Höhe $A_g$ und ist außerhalb Null.
- Die Spektralfunktion $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_g$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g$.
(2) Gaußimpuls ⇒ Gaussian Impulse
- Der Impuls $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $g(t= 0)=A_g$.
- Je kleiner die äquivalente Zeitdauer $\Delta t_g$ ist, um so breiter und niedriger ist das Spektrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$.
(3) Exponentialimpuls ⇒ Exponential Impulse
- Der Impuls ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$.
- $g(t)$ ist (stark) unsymmetrisch ⇒ das Spektrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig;
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/2$.
Weitere Angaben zu den betrachteten Impulsantworten
Die verschiedenen Empfangsfilter $H(f)$ werden durch ihre Impulsantworten $h(t)$ beschrieben.
Diese werden ähnlich wie die Eingangsimpulse $g(t)$ durch die Impulshöhe $A_h$, die äquivalente Impulsdauer $\Delta t_h$ sowie die Verzögerung $\tau_h$ gegenüber dem symmetrischen Fall gekennzeichnet. Die folgenden Kurzbeschreibungen gelten stets für $\tau_h= 0$.
(1) Spalt–Tiefpass ⇒ Rechteckförmige Impulsantwort
- Die Impulsantwort $h(t)$ hat im Bereich $\pm \Delta t_h/2$ die konstante Höhe $A_h$ und ist außerhalb Null.
- Der Frequenzgang $H(f)=K \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_h$.
- Bei Weißem Rauschen ist die Rauschvarianz am Filterausgang: $\sigma_d^2= N_0/2 \cdot A_h^2 \cdot \Delta t_h$.
(2) Gauß–Tiefpass ⇒ Gaußsche Impulsantwort
- Die Impulsantwort $h(t)=A_h\cdot {\rm e}^{-\pi\cdot(t/\Delta t_h)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $h(t= 0)=A_h$.
- Je kleiner die äquivalente Zeitdauer $\Delta t_h$ ist, um so breiter und niedriger ist der Frequenzgang $H(f)=K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_h)^2}$.
- Bei Weißem Rauschen ist die Rauschvarianz am Filterausgang: $\sigma_d^2= N_0/2 \cdot A_h^2 \cdot \Delta t_h/\sqrt{2}$.
(3) Tiefpass 1. Ordnung ⇒ Exponentiell abfallende Impulsantwort
- Die Impulsantwort ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $h(t)=A_h\cdot {\rm e}^{-t/\Delta t_h}$.
- $h(t)$ ist kausal und (stark) unsymmetrisch. Der Frequenzgang $H(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig.
- Bei Weißem Rauschen ist die Rauschvarianz am Filterausgang: $\sigma_d^2= N_0/4 \cdot A_h^2 \cdot \Delta t_h$.
(4) Extrem akausales Filter ⇒ Impulsantwort spiegelbildlich zu (3)
- Die Impulsantwort ist für $t>0$ identisch Null und für negative Zeiten unendlich weit ausgedehnt ⇒ $h(t)=A_h\cdot {\rm e}^{t/\Delta t_h}$ für $t<0$.
- Der Frequenzgang $H(f)$ ist konjugiert komplex zum Frequenzgang des Tiefpasses 1. Ordnung.
- Die Rauschvarianz am Filterausgang ist bei Weißem Rauschen genau so groß wie beim Tiefpass 1. Ordnung: $\sigma_d^2= N_0/4 \cdot A_h^2 \cdot \Delta t_h$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ... , 11) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
- Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen.
(1) Der Eingangsimpuls sei gaußförmig mit $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Welche Einstellung führt zum „Matched–Filter”? Wie groß ist $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$?
- Das Matched–Filter muss ebenfalls einen gaußförmigen Verlauf haben und es muss gelten: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$.
- Das (momentane) Signal–zu–Rauschleistungsverhältnis am Filterausgang ist $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB.
- Mit keinem anderen Filter als dem Matched–Filter ist dieses $\rm SNR$ (oder ein noch besseres) zu erreichen.
(2) Das Matched–Filter bei rechteckförmigen Eingangsimpuls mit $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ ist ein Spalt–Tiefpass ⇒ rechteckförmige Impulsantwort.
Wie groß ist hier $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? Interpretieren Sie alle dargestellten Grafiken und die numerischen Ergebnisse auf verschiedene Art und Weise.
- Die eingestellten Filterparameter sind $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB.
- Die Impulsenergie ist das Integral über $g^2(t)$ ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ ist hier implizit berücksichtigt.
- Eine andere Gleichung lautet: $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. Die Rauschvarianz kann z. B. als Integral über $h^2(t)$ berechnet werden: $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$.
- Das Nutzsignal $d_{\rm S} (t)= g(t) * h(t)$ hat einen dreieckförmigen Verlauf mit dem Maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$.
(3) Es gelten weiter die Einstellungen von (2) mit Ausnahme von $N_0=0.02 $ statt $N_0=0.01$. Welche Veränderungen sind erkennbar?
- Der einzige Unterschied ist die doppelt so große Rauschvarianz $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $T_{\rm D} = 0.1 $ statt $T_{\rm D, \ opt} = 0$. Wie wirkt sich dieser nichtoptimale Detektionszeitpunkt aus?
- Nun ist der Nutzabtastwert $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ kleiner ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. Es ergibt sich eine Verschlechterung um knapp ein dB.
- Für die weiteren Aufgaben wird vom optimalen Detektionszeitpunkt $T_{\rm D, \ opt}$ ausgegangen, wenn nicht explizit etwas anderes angegeben wird.
(5) Es gelten wieder die Einstellungen von (3) mit Ausnahme einer niedrigeren Impulsantwort $A_h = 0.8 $ statt $A_h = 1$. Interpretieren Sie die Veränderungen.
- Es handelt sich auch mit $A_h \ne A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
- Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber (3) jeweils um den Faktor $0.8^2$ vermindert wird.
(6) Gegenüber (5) wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$?
- Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} \approx 21.9$ dB.
- Der höhere Wert $21.9$ dB gegenüber (5) lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist.
(7) Wir gehen weiter von der Rechteck–Rechteck–Kombination aus mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=0$.
Interpretieren Sie die Ergebnisse nach Variation der äquivalenten Impulsdauer $\Delta t_h$ von $h(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_h$.
- Das Optimum ergibt sich erwartungsgemäß für die äquivalente Impulsdauer $\Delta t_h=\Delta t_g=1$. Dann ist $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$.
- Ist $\Delta t_h<\Delta t_g=1$, so ist das Nutzsignal trapezförmig. Für $\Delta t_h=0.6$: $d_{\rm S} (T_{\rm D}=0)= 0.6$ und $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 17.8$ dB.
- Auch für $\Delta t_h>1$ ist das Nutzsignal trapezförmig, aber trotzdem $d_{\rm S} (T_{\rm D}=0)= 1$. Die Rauschvarianz $\sigma_d^2$ nimmt kontinuierlich mit $\Delta t_h$ zu.
- Für $\Delta t_h=1.4$ ist $\sigma_d^2=0.0140$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 18.5$ dB. Gegenüber dem Matched–Filter $(\Delta t_h=1)$ beträgt die Verschlechterung ca. $1.5$ dB.
(8) Interpretieren Sie nun die Ergebnisse für verschiedene $\Delta t_g$ des Eingangsimpulses $g(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_g$.
- Beachten Sie: Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ ist die Differenz aus $20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (violette Kurve) und $20\cdot \lg \ \big [K \cdot \sigma_d \big ]$ (grüne Kurve).
- Beim betrachteten Parametersatz und $K=10$ ist der grüne Term $20\cdot \lg \ \big [K \cdot \sigma_d \big ] = 0$ dB für alle $\Delta t_g$ ⇒ die blaue und die violette Kurve sind identisch.
- Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ steigt von $15.6$ dB $($für $\Delta t_g = 0.6)$ bis $20$ dB $($für $\Delta t_g = 1)$ kontinuierlich an und bleibt für $\Delta t_g > 1$ dann konstant.
- Die Einstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ ergibt aber kein Matched-Filter. Vielmehr gilt mit $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB.
- Die Grafikdarstellung über $\Delta t_h$ mit der Grundeinstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ zeigt nun einen monotonen Anstieg der blauen Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$.
- Für $\Delta t_h = 0.6$ ergibt sich $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 17.8$ dB, für $\Delta t_h = 1.4$ dagegen $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 21.5$ dB $=10 \cdot \lg \ \rho_{\rm MF}$.
(9) Wir betrachten den Exponentialimpuls $g(t)$ und den Tiefpass erster Ordnung sowie $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=1$.
Erfüllt diese Einstellung den Matched-Filter-Kriterien? Begründen Sie Ihre Antworten mit möglichst vielen Argumenten.
- Hier gilt $h(t)=g(t)$. Bei einer Matched-Filter-Konfiguration müsste $h(t)={\rm const.} \cdot g(T_{\rm D}-t)$ gelten.
- Das Detektionsnutzsignal $d_{\rm S}(t)$ hat keinen symmetrischen Verlauf um das Maximum. Beim Matched-Filter müsste $d_{\rm S}(T_{\rm D}-t) = d_{\rm S}(T_{\rm D}+t) $ gelten.
- Trotz $\Delta t_h=\Delta t_g$ ist $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) \approx 14.3$ dB kleiner als $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 \approx 17$ dB.
(10) Was ändert sich bei sonst gleichen Einstellungen mit dem „extrem akausalen Filter”? Erfüllt die Einstellung die Matched-Filter-Kriterien? Begründung.
- Hier gilt nun $h(t)=g(-t)$ und das Detektionsnutzsignal $d_{\rm S}(t)$ ist symmetrisch um $t=0$. Sinnvollerweise sollte hier $T_{\rm D} = 0 $ gewählt werden.
- Damit erhält man für $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) =10 \cdot \lg \ d_{\rm S}^2 (T_{\rm D,\ opt})/\sigma_d^2 = 17$ dB den gleichen Wert wie für $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 = 17$ dB.
- Das Nutzsignal $d_{\rm S}(t)$ ist formgleich mit der Energie–AKF des Sendeimulses $g(t)$. Das Matched-Filter bündelt die Energie um den geeigneten Zeitpunkt $T_{\rm D,\ opt}$.
(11) Mit welchem Rechteckimpuls $g(t)$ erreicht man mit dem entsprechend angepassten Filter das gleiche $\rho _{\rm MF}=50$ wie in Aufgabe (10)?
Mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=0.5$ oder mit $A_h=A_g=0.5,\ \Delta t_h=\Delta t_g=1$ ?
- Aus der Gleichung $\rho _{\rm MF} = 2 \cdot E_g/N_0$ geht bereits hervor, dass das SNR nur von der Energie $E_g$ des Eingangsimpulses abhängt und nicht von dessen Form.
- Der Exponentialimpuls mit $A_g=1,\ \Delta t_g=1$ hat die Energie $E_g=0.5$. Der Rechteckimpuls mit $A_g=1,\ \Delta t_g=0.5$ ebenfalls ⇒ $\rho _{\rm MF}=50$.
- Dagegen besitzt der Rechteckimpuls mit $A_g=0.5,\ \Delta t_g=1$ eine kleinere Energie ⇒ $E_g=0.25$ ⇒ $\rho _{\rm MF}=25$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} = 14$ dB.
Zur Handhabung des Applets
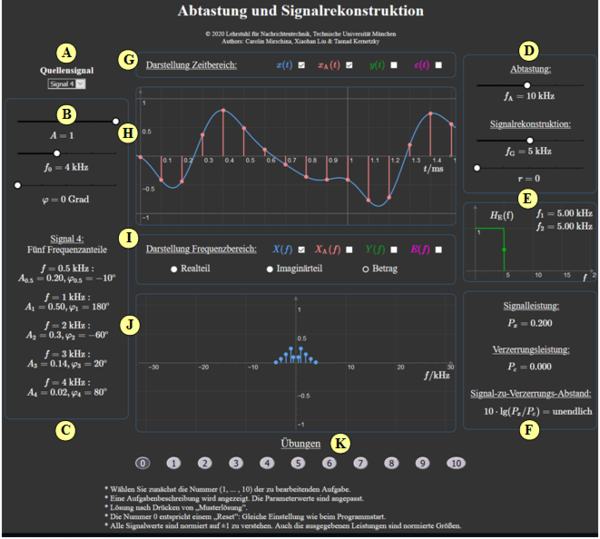
(A) Auswahl eines von vier Quellensignalen
(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)
(C) Ausgabe der verwendeten Programmparameter
(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$
(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$
(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$
(G) Darstellungsauswahl für Zeitbereich
(H) Grafikbereich für Zeitbereich
( I ) Darstellungsauswahl für Frequenzbereich
(J) Grafikbereich für Frequenzbereich
(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger im Rahmen seiner Diplomarbeit (LB) mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.