|
|
| Zeile 3: |
Zeile 3: |
| | ==Programmbeschreibung== | | ==Programmbeschreibung== |
| | <br> | | <br> |
| − | In diesem Applet werden binäre $(M=2)$ und ternäre $(M=3)$ Kanalmodelle ohne Gedächtnis betrachtet mit jeweils $M$ Eingängen $X$ und $M$ Ausgängen $Y$. Ein solches Nachrichtensystem ist durch die Wahrscheinlichkeitsfunktion $P_X(X)$ und die Matrix $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ der Übergangswahrscheinlichkeiten vollständig bestimmt.
| |
| | | | |
| − | Für diese binären bzw. ternären Systeme werden folgende informationstheoretische Beschreibungsgrößen hergeleitet und verdeutlicht:
| |
| − | *die ''Quellenentropie'' $H(X)$ und die ''Sinkenentropie'' $H(Y)$,
| |
| − | *die ''Äquivokation'' („Rückschlussentropie”) $H(X|Y)$ und die ''Irrelevanz'' („Streuentropie”) $H(Y|X)$,
| |
| − | *die ''Verbundentropie'' $H(XY)$ sowie die ''Transinformation'' (englisch: ''Mutual Information'') $I(X; Y)$,
| |
| − | *die ''Kanalkapazität'' als die entscheidende Kenngröße digitaler Kanalmodelle ohne Gedächtnis:
| |
| − | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
| |
| − |
| |
| − | Diese informationstheoretische Größen können sowohl in analytische geschlossener Form berechnet oder durch Auswertung von Quellen– und Sinkensymbolfolge simulativ ermittelt werden.
| |
| | | | |
| | ==Theoretischer Hintergrund== | | ==Theoretischer Hintergrund== |
| | <br> | | <br> |
| − | ===Erwartungswerte zweidimensionaler Zufallsgrößen=== | + | ===Erwartungswerte von 2D–Zufallsgrößen und Korrelationskoeffizient=== |
| − | <br>
| + | |
| − | Ein Sonderfall der statistischen Abhängigkeit ist die ''Korrelation''. | + | Wir betrachten eine zweidimensionale $\rm (2D)$–Zufallsgröße $(XY)$ mit der Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten $X$ und $Y$ statistische Abhängigkeiten bestehen. Ein Sonderfall ist die ''Korrelation''. |
| | | | |
| | {{BlaueBox|TEXT= | | {{BlaueBox|TEXT= |
| − | $\text{Definition:}$ Unter '''Korrelation''' versteht man eine ''lineare Abhängigkeit'' zwischen den Einzelkomponenten $x$ und $y$. | + | $\text{Definition:}$ Unter '''Korrelation''' versteht man eine ''lineare Abhängigkeit'' zwischen den Einzelkomponenten $X$ und $Y$. |
| | *Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig. | | *Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig. |
| − | *Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.}} | + | *Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.}} |
| | | | |
| | | | |
| − | Zur quantitativen Erfassung der Korrelation verwendet man verschiedene Erwartungswerte der 2D-Zufallsgröße $(x, y)$. | + | Für das Folgende setzen wir voraus, dass $X$ und $Y$ mittelwertfrei seien ${\rm E}\big [ X \big ] = {\rm E}\big [ Y \big ]=0$. Zur Beschreibung der Korrelation genügen dann folgende Erwartungswerte: |
| | + | * die '''Varianzen''' in $X$– bzw. in $Y$–Richtung: |
| | + | :$$\sigma_X^2= {\rm E}\big [ X^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}x^2 \cdot f_{X}(x) \, {\rm d}x\hspace{0.05cm},\hspace{0.5cm}\sigma_Y^2= {\rm E}\big [Y^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}y^2 \cdot f_{Y}(y) \, {\rm d}y\hspace{0.05cm};$$ |
| | + | * die '''Kovarianz''' zwischen den Einzelkomponenten $X$ und $Y$: |
| | + | :$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\ \cdot y \cdot f_{XY}(x,y) \, {\rm d}x\, {\rm d}y\hspace{0.05cm}.$$ |
| | | | |
| − | Diese sind analog definiert zum eindimensionalen Fall
| + | Bei statististischer Unabhängigkeit der beiden Komponenten $X$ und $Y$ ist die Kovarianz $\mu_{XY} \equiv 0$. |
| − | *gemäß [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße|Kapitel 2]] (bei wertdiskreten Zufallsgrößen) | + | |
| − | *bzw. [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Kapitel 3]] (bei wertkontinuierlichen Zufallsgrößen):
| + | *Das Ergebnis $\mu_{XY} = 0$ ist aber auch bei statistisch abhängigen Komponenten $X$ und $Y$ möglich, nämlich dann, wenn diese unkorreliert, also ''linear unabhängig'' sind. |
| − | | + | *Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $Y=X^2.$ |
| | | | |
| − | {{BlaueBox|TEXT=
| |
| − | $\text{Definition:}$ Für die (nichtzentrierten) '''Momente''' gilt die Beziehung:
| |
| − | :$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$
| |
| − | Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$ }}
| |
| | | | |
| | + | Man spricht von '''vollständiger Korrelation''', wenn die (deterministische) Abhängigkeit zwischen $X$ und $Y$ durch die Gleichung $Y = K · X$ ausgedrückt wird. Dann ergibt sich für die Kovarianz: |
| | + | * $\mu_{XY} = σ_X · σ_Y$ bei positivem Wert von $K$, |
| | + | * $\mu_{XY} = -σ_X · σ_Y$ bei negativem $K$–Wert. |
| | | | |
| − | {{BlaueBox|TEXT=
| |
| − | $\text{Definition:}$ Die auf $m_x$ bzw. $m_y$ bezogenen '''Zentralmomente''' lauten:
| |
| − | :$$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$
| |
| − | In dieser allgemein gültigen Definitionsgleichung sind die Varianzen $σ_x^2$ und $σ_y^2$ der zwei Einzelkomponenten durch $\mu_{20}$ bzw. $\mu_{02}$ mit enthalten. }}
| |
| | | | |
| | + | Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten. |
| | | | |
| | {{BlaueBox|TEXT= | | {{BlaueBox|TEXT= |
| − | $\text{Definition:}$ Besondere Bedeutung besitzt die '''Kovarianz''' $(k = l = 1)$, die ein Maß für die ''lineare statistische Abhängigkeit'' zwischen den Zufallsgrößen $x$ und $y$ ist: | + | $\text{Definition:}$ Der '''Korrelationskoeffizient''' ist der Quotient aus der Kovarianz $\mu_{XY}$ und dem Produkt der Effektivwerte $σ_X$ und $σ_Y$ der beiden Komponenten: |
| − | :$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$ | + | :$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}.$$}} |
| − | Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht.}}
| |
| | | | |
| | | | |
| − | ''Anmerkungen:''
| + | Der Korrelationskoeffizient $\rho_{XY}$ weist folgende Eigenschaften auf: |
| − | *Die Kovarianz $\mu_{11}=\mu_{xy}$ hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen: | + | *Aufgrund der Normierung gilt stets $-1 \le ρ_{XY} ≤ +1$. |
| − | :$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$
| + | *Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{XY} = 0$. |
| | + | *Bei strenger linearer Abhängigkeit zwischen $X$ und $Y$ ist $ρ_{XY}= ±1$ ⇒ vollständige Korrelation. |
| | + | *Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $X$–Wert im statistischen Mittel auch $Y$ größer ist als bei kleinerem $X$. |
| | + | *Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $Y$ mit steigendem $X$ im Mittel kleiner wird. |
| | | | |
| − | *Diese Gleichung ist für numerische Auswertungen enorm vorteilhaft, da $m_{xy}$, $m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ in einem einzigen Durchlauf gefunden werden können.
| |
| − | *Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und könnte dann erst in einem zweiten Durchlauf den Erwartungswert ${\rm E}\big[(x - m_x) · (y - m_y)\big]$ berechnen.
| |
| | | | |
| − | | + | [[Datei:Korrelation_1a.png|right|frame| 2D-WDF $f_{XY}(x, y)$ sowie die zugehörigen Randwahrscheinlichkeitsdichten $f_{X}(x)$ und $f_{Y}(y)$]] |
| − | [[Datei:P_ID628__Sto_T_4_1_S6Neu.png |right|frame| Beispielhafte 2D-Erwartungswerte]] | |
| | {{GraueBox|TEXT= | | {{GraueBox|TEXT= |
| − | $\text{Beispiel 4:}$ In den beiden ersten Zeilen der Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben. | + | $\text{Beispiel 1:}$ Die 2D–Zufallsgröße $XY$ sei diskret und kann nur vier verschiedene Werte annehmen: |
| − |
| + | *$(+0.5,\ 0)$ sowie $(-0.5,\ 0)$ jeweils mit der Wahrscheinlichkeit $0.3$, |
| − | *Durch Mittelung über die jeweils zehn Folgenelemente erhält man | + | *$(+1,\ +1)$ sowie $(+1,\ -1)$ jeweils mit der Wahrscheinlichkeit $0.2$. |
| − | :$$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$
| |
| − | *Daraus ergibt sich direkt der Wert für die Kovarianz:
| |
| − | :$$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$
| |
| − | <br clear=all>
| |
| − | Ohne Kenntnis der Gleichung $\mu_{xy} = m_{xy} - m_x · m_y$ hätte man zunächst im ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln müssen, <br>um dann in einem zweiten Durchlauf die Kovarianz $\mu_{xy}$ als Erwartungswert des Produkts der mittelwertfreien Größen bestimmen zu können.}}
| |
| − | | |
| − | ===Korrelationskoeffizient===
| |
| − | <br>
| |
| − | Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten|WDF und VTF bei statistisch unabhängigen Komponenten]] betrachtet.
| |
| | | | |
| − | *Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also ''linear unabhängig'' sind.
| |
| − | *Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$
| |
| | | | |
| | + | $\rm (A)$ Die Varianzen bzw. die Streuungen können aus $f_{X}(x)$ und $f_{Y}(y)$ berechnet werden: |
| | + | :$$\sigma_X^2 = 2 \cdot \big [0.2 \cdot 1^2 + 0.3 \cdot 0.5^2 \big] = 0.55\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_X = 0.7416,$$ |
| | + | :$$\sigma_Y^2 = \big [0.2 \cdot (-1)^2 + 0.6 \cdot 0^2 +0.2 \cdot (+1)^2 \big] = 0.4\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_Y = 0.6324.$$ |
| | | | |
| − | Man spricht von '''vollständiger Korrelation''', wenn die (deterministische) Abhängigkeit zwischen $x$ und $y$ durch die Gleichung $y = K · x$ ausgedrückt wird. Dann ergibt sich für die Kovarianz:
| + | $\rm (B)$ Für die Kovarianz ergibt sich der folgende Erwartungswert: |
| − | * $\mu_{xy} = σ_x · σ_y$ bei positivem Wert von $K$,
| + | :$$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = 2 \cdot \big [0.2 \cdot 1 \cdot 1 + 0.3 \cdot 0.5 \cdot 0 \big] = 0.4.$$ |
| − | * $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert.
| |
| | | | |
| | + | $\rm (C)$ Damit erhält man für den Korrelationskoeffizient: |
| | + | :$$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}=\frac{0.4 } {0.7416 \cdot 0.6324 }\approx 0.853. |
| | + | $$}} |
| | + | <br clear=all> |
| | | | |
| − | Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.
| + | ===Dummy=== |
| − | | |
| − | {{BlaueBox|TEXT=
| |
| − | $\text{Definition:}$ Der '''Korrelationskoeffizient''' ist der Quotient aus der Kovarianz $\mu_{xy}$ und dem Produkt der Effektivwerte $σ_x$ und $σ_y$ der beiden Komponenten:
| |
| − | :$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$}}
| |
| − | | |
| | | | |
| − | Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf:
| |
| − | *Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$.
| |
| − | *Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$.
| |
| − | *Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$ ⇒ vollständige Korrelation.
| |
| − | *Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
| |
| − | *Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird.
| |
| | | | |
| | | | |
| − | [[Datei:P_ID232__Sto_T_4_1_S7a_neu.png |right|frame| Gaußsche 2D-WDF mit Korrelation]]
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 5:}$ Es gelten folgende Voraussetzungen:
| |
| − | *Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF.
| |
| − | *Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$.
| |
| − | *Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$.
| |
| − |
| |
| − |
| |
| − | Im Unterschied zum [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten| Beispiel 2]] mit statistisch unabhängigen Komponenten ⇒ $ρ_{xy} = 0$ $($trotz $σ_y < σ_x)$ erkennt man, dass hier bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.}}
| |
| | | | |
| | | | |
| Zeile 132: |
Zeile 97: |
| | *Das interaktive Applet [[Applets:Korrelationskoeffizient_%26_Regressionsgerade|Korrelationskoeffizient und Regressionsgerade]] verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird: | | *Das interaktive Applet [[Applets:Korrelationskoeffizient_%26_Regressionsgerade|Korrelationskoeffizient und Regressionsgerade]] verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird: |
| | :$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$ | | :$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$ |
| − | ===Zugrunde liegendes Modell der Digitalsignalübertragung ===
| |
| − |
| |
| − | Die Menge der möglichen '''Quellensymbole''' wird durch die diskrete Zufallsgröße $X$ charakterisiert.
| |
| − | *Im binären Fall ⇒ $M_X= |X| = 2$ gilt $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B} \hspace{0.05cm}\}$ mit der Wahrscheinlichkeitsfunktion $($englisch: ''Probability Mass Function'', $\rm PMF)$ $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B}\big)$ sowie den Quellensymbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}=1- p_{\rm A}$.
| |
| − | *Entsprechend gilt für eine Ternärquelle ⇒ $M_X= |X| = 3$: $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B}, \hspace{0.15cm} {\rm C} \hspace{0.05cm}\}$, $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B},\hspace{0.15cm}p_{\rm C}\big)$, $p_{\rm C}=1- p_{\rm A}-p_{\rm B}$.
| |
| − |
| |
| − |
| |
| − | Die Menge der möglichen '''Sinkensymbole''' wird durch die diskrete Zufallsgröße $Y$ charakterisiert. Diese entstammen der gleichen Symbolmenge wie die Quellensymbole ⇒ $M_Y=M_X = M$. Zur Vereinfachung der nachfolgenden Beschreibung bezeichnen wir diese mit Kleinbuchstaben, zum Beispiel für $M=3$: $Y = \{\hspace{0.05cm}{\rm a}, \hspace{0.15cm} {\rm b}, \hspace{0.15cm} {\rm c} \hspace{0.05cm}\}$.
| |
| − |
| |
| − | Der Zusammenhang zwischen den Zufallsgrößen $X$ und $Y$ ist durch ein '''digitales Kanalmodell ohne Gedächtnis''' $($englisch: ''Discrete Memoryless Channel'', $\rm DMC)$ festgelegt. Die linke Grafik zeigt dieses für $M=2$ und die rechte Grafik für $M=3$.
| |
| − |
| |
| − | [[Datei:Transinf_1_neu.png|center|frame|Digitales Kanalmodell für $M=2$ (links) und für $M=3$ (rechts). <br>Bitte beachten Sie: In der rechten Grafik sind nicht alle Übergänge beschriftet]]
| |
| − |
| |
| − | Die folgende Beschreibung gilt für den einfacheren Fall $M=2$. Für die Berechnung aller informationstheoretischer Größen im nächsten Abschnitt benötigen wir außer $P_X(X)$ und $P_Y(Y)$ noch die zweidimensionalen Wahrscheinlichkeitsfunktionen $($jeweils eine $2\times2$–Matrix$)$ aller
| |
| − | # [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#Bedingte_Wahrscheinlichkeit|bedingten Wahrscheinlichkeiten]] ⇒ $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ ⇒ durch das DMC–Modell vorgegeben;
| |
| − | # [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Verbundwahrscheinlichkeit_und_Verbundentropie|Verbundwahrscheinlichkeiten]] ⇒ $P_{XY}(X,\hspace{0.1cm}Y)$;
| |
| − | # [[Stochastische_Signaltheorie/Statistische_Abhängigkeit_und_Unabhängigkeit#R.C3.BCckschlusswahrscheinlichkeit|Rückschlusswahrscheinlichkeiten]] ⇒ $P_{\hspace{0.01cm}X\hspace{0.03cm} \vert \hspace{0.03cm}Y}(X\hspace{0.03cm} \vert \hspace{0.03cm} Y)$.
| |
| − |
| |
| − |
| |
| − | [[Datei:Transinf_2.png|right|frame|Betrachtetes Modell des Binärkanals]]
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 1}$: Wir betrachten den skizzierten Binärkanal.
| |
| − | * Die Verfälschungswahrscheinlichkeiten seien:
| |
| − |
| |
| − | :$$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\
| |
| − | p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
| |
| − |
| |
| − | :$$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) =
| |
| − | \begin{pmatrix}
| |
| − | 0.95 & 0.05\\
| |
| − | 0.4 & 0.6
| |
| − | \end{pmatrix} \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Außerdem gehen wir von nicht gleichwahrscheinlichen Quellensymbolen aus:
| |
| − |
| |
| − | :$$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )=
| |
| − | \big ( 0.1,\ 0.9 \big )
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Für die Wahrscheinlichkeitsfunktion der Sinke ergibt sich somit:
| |
| − |
| |
| − | :$$P_Y(Y) = \big [ {\rm Pr}( Y\hspace{-0.1cm} = {\rm a})\hspace{0.05cm}, \ {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) \big ] = \big ( 0.1\hspace{0.05cm},\ 0.9 \big ) \cdot
| |
| − | \begin{pmatrix}
| |
| − | 0.95 & 0.05\\
| |
| − | 0.4 & 0.6
| |
| − | \end{pmatrix} $$
| |
| − |
| |
| − | :$$\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) =
| |
| − | 0.1 \cdot 0.95 + 0.9 \cdot 0.4 = 0.455\hspace{0.05cm},\hspace{1.0cm}
| |
| − | {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) = 1 - {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) = 0.545.$$
| |
| − |
| |
| − | *Die Verbundwahrscheinlichkeiten $p_{\mu \kappa} = \text{Pr}\big[(X = μ) ∩ (Y = κ)\big]$ zwischen Quelle und Sinke sind:
| |
| − |
| |
| − | :$$\begin{align*}p_{\rm Aa} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.095\hspace{0.05cm},\hspace{0.5cm}p_{\rm Ab} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.005\hspace{0.05cm},\\
| |
| − | p_{\rm Ba} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.360\hspace{0.05cm},
| |
| − | \hspace{0.5cm}p_{\rm Bb} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.540\hspace{0.05cm}.
| |
| − | \end{align*}$$
| |
| − |
| |
| − | :$$\Rightarrow \hspace{0.3cm} P_{XY}(X,\hspace{0.1cm}Y) =
| |
| − | \begin{pmatrix}
| |
| − | 0.095 & 0.005\\
| |
| − | 0.36 & 0.54
| |
| − | \end{pmatrix} \hspace{0.05cm}.$$
| |
| − |
| |
| − | * Für die Rückschlusswahrscheinlichkeiten erhält man:
| |
| − |
| |
| − | :$$\begin{align*}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Aa}/p_{\rm a} = 0.095/0.455 = 0.2088\hspace{0.05cm},\hspace{0.5cm}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Ab}/p_{\rm b} = 0.005/0.545 = 0.0092\hspace{0.05cm},\\
| |
| − | p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Ba}/p_{\rm a} = 0.36/0.455 = 0.7912\hspace{0.05cm},\hspace{0.5cm}p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Bb}/p_{\rm b} = 0.54/0.545 = 0.9908\hspace{0.05cm}
| |
| − | \end{align*}$$
| |
| − |
| |
| − | :$$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}X\hspace{0.05cm} \vert \hspace{0.05cm}Y}(X\hspace{0.05cm} \vert \hspace{0.05cm} Y) =
| |
| − | \begin{pmatrix}
| |
| − | 0.2088 & 0.0092\\
| |
| − | 0.7912 & 0.9908
| |
| − | \end{pmatrix} \hspace{0.05cm}.$$ }}
| |
| − | <br clear=all><br><br>
| |
| − | ===Definition und Interpretation verschiedener Entropiefunktionen ===
| |
| − |
| |
| − | Im [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen|$\rm LNTwww$–Theorieteil]] werden alle für 2D–Zufallsgrößen relevanten Entropien definiert, die auch für die Digitalsignalübertragung gelten. Zudem finden Sie dort zwei Schaubilder, die den Zusammenhang zwischen den einzelnen Entropien illustrieren.
| |
| − | *Für die Digitalsignalübertragung ist die rechte Darstellung zweckmäßig, bei der die Richtung von der Quelle $X$ zur Sinke $Y$ erkennbar ist.
| |
| − | *Wir interpretieren nun ausgehend von dieser Grafik die einzelnen informationstheoretischen Größen.
| |
| − |
| |
| − |
| |
| − | [[Datei:P_ID2781__Inf_T_3_3_S2.png|center|frame|Zwei informationstheoretische Modelle für die Digitalsignalübertragung.
| |
| − | <br>Bitte beachten Sie: In der rechten Grafik ist $H_{XY}$ nicht darstellbar]]
| |
| − |
| |
| − | *Die '''Quellenentropie''' (englisch: ''Source Entropy'' ) $H(X)$ bezeichnet den mittleren Informationsgehalt der Quellensymbolfolge. Mit dem Symbolumfang $|X|$ gilt:
| |
| − |
| |
| − | :$$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm}
| |
| − | = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\big ] \hspace{0.2cm}
| |
| − | =\hspace{0.2cm} \sum_{\mu = 1}^{|X|}
| |
| − | P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Die '''Äquivokation''' (auch ''Rückschlussentropie'' genannt, englisch: ''Equivocation'' ) $H(X|Y)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Sinke $Y$ genau Bescheid weiß, durch Beobachtung der Quelle $X$ gewinnt:
| |
| − |
| |
| − | :$$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|}
| |
| − | P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y}
| |
| − | (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})}
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Die Äquivokation ist der Anteil der Quellenentropie $H(X)$, der durch Kanalstörungen (bei digitalem Kanal: Übertragungsfehler) verloren geht. Es verbleibt die '''Transinformation''' (englisch: ''Mutual Information'') $I(X; Y)$, die zur Sinke gelangt:
| |
| − |
| |
| − | :$$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|}
| |
| − | P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa})}{P_{\hspace{0.05cm}X}(\hspace{0.05cm}x_{\mu}) \cdot P_{\hspace{0.05cm}Y}(\hspace{0.05cm}y_{\kappa})}
| |
| − | \hspace{0.05cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$
| |
| − |
| |
| − | '''Hallo Veronika, bitte diese Gleichung an Beispielen überprüfen und mir zeigen, wie es geht. Ich stelle mich zu blöd!'''
| |
| − |
| |
| − | *Die '''Irrelevanz''' (manchmal auch ''Streuentropie'' genannt, englisch: ''Irrelevance'') $H(Y|X)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Quelle $X$ genau Bescheid weiß, durch Beobachtung der Sinke $Y$ gewinnt:
| |
| − |
| |
| − | :$$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|}
| |
| − | P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X}
| |
| − | (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})}
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Die '''Sinkenentropie''' $H(Y)$, der mittlere Informationsgehalt der Sinke, ist die Summe aus der nützlichen Transinformation $I(X; Y)$ und der Irrelevanz $H(Y|X)$, die ausschließlich von Kanalfehlern herrührt:
| |
| − |
| |
| − | :$$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm}
| |
| − | = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\big ] \hspace{0.2cm} =I(X;Y) + H(Y|X)
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | *Die '''Verbundentropie''' $H(XY)$ gibt ist den mittleren Informationsgehalt der 2D–Zufallsgröße $XY$ an.  sie beschreibt zudem eine obere Schranke für die Summe aus Quellenentropie und Sinkenentropie:
| |
| − |
| |
| − | :$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm}
| |
| − | P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})}\le H(X) + H(Y) \hspace{0.05cm}.$$
| |
| − |
| |
| − | [[Datei:Transinf_2.png|right|frame|Betrachtetes Modell des Binärkanals]]
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 2}$: Es gelten die gleichen Voraussetzungen wie für das [[Applets:Transinformation_bei_binären_und_ternären_Nachrichtensystemen#Zugrunde_liegendes_Modell_der_Digitalsignal.C3.BCbertragung|$\text{Beispiel 1}$]]:
| |
| − |
| |
| − | '''(1)''' Die Quellensymbole sind nicht gleichwahrscheinlich:
| |
| − | :$$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )=
| |
| − | \big ( 0.1,\ 0.9 \big )
| |
| − | \hspace{0.05cm}.$$
| |
| − | '''(2)''' Die Verfälschungswahrscheinlichkeiten seien:
| |
| − | :$$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\
| |
| − | p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
| |
| − |
| |
| − | :$$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) =
| |
| − | \begin{pmatrix}
| |
| − | 0.95 & 0.05\\
| |
| − | 0.4 & 0.6
| |
| − | \end{pmatrix} \hspace{0.05cm}.$$
| |
| − |
| |
| − | [[Datei:Inf_T_1_1_S4_vers2.png|frame|Binäre Entropiefunktion als Funktion von $p$|right]]
| |
| − | *Wegen Voraussetzung '''(1)''' erhält man so für die Quellenentropie mit der [[Informationstheorie/Gedächtnislose_Nachrichtenquellen#Bin.C3.A4re_Entropiefunktion|binären Entropiefunktion]] $H_{\rm bin}(p)$:
| |
| − |
| |
| − | :$$H(X) = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm A}\hspace{0.1cm} } + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_{\rm B} }= H_{\rm bin} (p_{\rm A}) = H_{\rm bin} (0.1)= 0.469 \ {\rm bit}
| |
| − | \hspace{0.05cm};$$
| |
| − |
| |
| − | ::$$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + (1 - p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1 - p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)}
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | * Entsprechend gilt für die Sinkenentropie mit der PMF $P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b} \big )=
| |
| − | \big ( 0.455,\ 0.545 \big )$:
| |
| − | :$$H(Y) = H_{\rm bin} (0.455)= 0.994 \ {\rm bit}
| |
| − | \hspace{0.05cm}.$$
| |
| − | *Als nächstes berechnen wir die Verbundentropie:
| |
| − | :$$H(XY) = p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+ p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }+p_{\rm Ba} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ba}\hspace{0.1cm} }+ p_{\rm Bb} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Bb}\hspace{0.1cm} }$$
| |
| − | :$$\Rightarrow \hspace{0.3cm}H(XY) = 0.095 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.095 } +0.005 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.005 }+0.36 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.36 }+0.54 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.54 }= 1.371 \ {\rm bit}
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | Entsprechend dem oberen linken Schaubild sind somit auch die restlichen informationstheoretischen Größen berechenbar:
| |
| − | [[Datei:Transinf_4.png|right|frame|Informationstheoretisches Modell für $\text{Beispiel 2}$]]
| |
| − |
| |
| − | *die '''Äquivokation''' (oder Rückschlussentropie):
| |
| − |
| |
| − | :$$H(X \vert Y) \hspace{-0.01cm} =\hspace{-0.01cm} H(XY) \hspace{-0.01cm} -\hspace{-0.01cm} H(Y) \hspace{-0.01cm} = \hspace{-0.01cm} 1.371\hspace{-0.01cm} -\hspace{-0.01cm} 0.994\hspace{-0.01cm} =\hspace{-0.01cm} 0.377\ {\rm bit}
| |
| − | \hspace{0.05cm},$$
| |
| − |
| |
| − | *die '''Irrelevanz''' (oder Streuentropie):
| |
| − |
| |
| − | :$$H(Y \vert X) = H(XY) - H(X) = 1.371 - 0.994 = 0.902\ {\rm bit}
| |
| − | \hspace{0.05cm}.$$
| |
| − |
| |
| − | *die '''Transinformation''' (englisch ''Mutual Information''):
| |
| − |
| |
| − | :$$I(X;Y) = H(X) + H(Y) - H(XY) = 0.469 + 0.994 - 1.371 = 0.092\ {\rm bit}
| |
| − | \hspace{0.05cm},$$
| |
| − |
| |
| − | Die Ergebnisse sind in nebenstehender Grafik zusammengefasst.
| |
| − |
| |
| − | ''Anmerkung'': Äquivokation und Irrelevanz könnte man (allerdfings mit Mehraufwand) auch direkt aus den entsprechenden Wahrscheinlichkeitsfunktionen berechnen, zum Beispiel:
| |
| − |
| |
| − | :$$H(Y \vert X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}\vert \hspace{0.03cm}X}
| |
| − | (\hspace{0.05cm}y\hspace{0.03cm} \vert \hspace{0.05cm} x)}= p_{\rm Aa} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} } +
| |
| − | p_{\rm Ab} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} } +
| |
| − | p_{\rm Ba} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} } +
| |
| − | p_{\rm Bb} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} } = 0.902 \ {\rm bit} \hspace{0.05cm}.$$}}
| |
| − |
| |
| − |
| |
| − | [[Datei:Transinf_3.png|right|frame|Betrachtetes Modell des Ternärkanals:<br>Rote Übergänge stehen für $p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}C} = q$ und blaue für $p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}A} =\text{...}= p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}C}= (1-q)/2$]]
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 3}$: Nun betrachten wir ein Übertragungssystem mit $M_X = M_Y = M=3$.
| |
| − |
| |
| − | '''(1)''' Die Quellensymbole seien gleichwahrscheinlich:
| |
| − | :$$P_X(X) = \big ( p_{\rm A},\ p_{\rm B},\ p_{\rm C} \big )=
| |
| − | \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(X)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit}
| |
| − | \hspace{0.05cm}.$$
| |
| − | '''(2)''' Das Kanalmodell ist symmetrisch ⇒ auch die Sinkensymbole sind gleichwahrscheinlich:
| |
| − | :$$P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b},\ p_{\rm c} \big )=
| |
| − | \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(Y)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit}
| |
| − | \hspace{0.05cm}.$$
| |
| − | '''(3)''' Die Verbundwahrscheinlichkeiten ergeben sich wie folgt:
| |
| − | :$$p_{\rm Aa}= p_{\rm Bb}= p_{\rm Cc}= q/M,$$
| |
| − | :$$p_{\rm Ab}= p_{\rm Ac}= p_{\rm Ba}= p_{\rm Bc} = p_{\rm Ca}= p_{\rm Cb} = (1-q)/(2M)$$
| |
| − | :$$\Rightarrow\hspace{0.30cm}H(XY) = 3 \cdot p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+6 \cdot p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }= \
| |
| − | \text{...} \ = q \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{q }+ (1-q) \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{(1-q)/2 }.$$
| |
| − | [[Datei:Transinf_10.png|right|frame|Einige Ergebnisse zum $\text{Beispiel 3}$]]
| |
| − | '''(4)''' Für die Transinformation erhält man nach einigen Umformungen unter Berücksichtigung der Gleichung
| |
| − | :$$I(X;Y) = H(X) + H(Y) - H(XY)\text{:}$$
| |
| − | :$$I(X;Y) = {\rm log_2}\ (M) - (1-q) -H_{\rm bin}(q).$$
| |
| − | * Bei fehlerfreier Ternärübertragung $(q=1)$ gilt $I(X;Y) = H(X) = H(Y)={\rm log_2}\hspace{0.1cm}3$.
| |
| − | * Mit $q=0.8$ sinkt die Transinformaion schon auf $I(X;Y) = 0.663$ und mit $q=0.5$ auf $0.085$ bit.
| |
| − | *Der ungünstigste Fall aus informationstheoretischer Sicht ist $q=1/3$ ⇒ $I(X;Y) = 0$.
| |
| − | *Dagegen ist der aus der aus Sicht der Übertragungstheorie ungünstigste Fall $q=0$ ⇒ „kein einziges Übertragungssymbol kommt richtig an” aus informationstheoretischer Sicht gar nicht so schlecht.
| |
| − | * Um dieses gute Ergebnis nutzen zu können, ist allerdings sendeseitig eine Kanalcodierung erforderlich. }}
| |
| − | <br><br>
| |
| − | ===Definition und Bedeutung der Kanalkapazität ===
| |
| − |
| |
| − | Berechnet man die Transinformation $I(X, Y)$ wie zuletzt im $\text{Beispiel 2}$ ausgeführt, so hängt diese nicht nur vom diskreten gedächtnislosen Kanal (englisch: ''Discrete Memoryless Channel'', kurz DMC) ab, sondern auch von der Quellenstatistik ⇒ $P_X(X)$ ab. Ergo: '''Die Transinformation''' $I(X, Y)$ ''' ist keine reine Kanalkenngröße'''.
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | $\text{Definition:}$ Die von [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] eingeführte '''Kanalkapazität''' (englisch: ''Channel Capacity'') lautet gemäß seinem Standardwerk [Sha48]<ref name = ''Sha48''>Shannon, C.E.: ''A Mathematical Theory of Communication''. In: Bell Syst. Techn. J. 27 (1948), S. 379-423 und S. 623-656.</ref>:
| |
| − |
| |
| − | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
| |
| − |
| |
| − | Oft wird die Zusatzeinheit „bit/Kanalzugriff” hinzugefügt, bei englischen Texten „bit/use”. Da nach dieser Definition stets die bestmögliche Quellenstatistik zugrunde liegt, hängt $C$ nur von den Kanaleigenschaften ⇒ $P_{Y \vert X}(Y \vert X)$ ab, nicht jedoch von der Quellenstatistik ⇒ $P_X(X)$. }}
| |
| − |
| |
| − |
| |
| − | Shannon benötigte die Kanalbeschreibungsgröße $C$ zur Formulierung des Kanalcodierungstheorems – eines der Highlights der von ihm begründeten Informationstheorie.
| |
| − |
| |
| − | {{BlaueBox|TEXT=
| |
| − | $\text{Shannons Kanalcodierungstheorem:}$
| |
| − | *Zu jedem Übertragungskanal mit der Kanalkapazität $C > 0$ existiert (mindestens) ein $(k, n)$–Blockcode, dessen (Block–)Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R = k/n$ kleiner oder gleich der Kanalkapazität ist: $R ≤ C.$
| |
| − | * Voraussetzung hierfür ist allerdings, dass für die Blocklänge dieses Codes gilt: $n → ∞.$
| |
| − |
| |
| − |
| |
| − | $\text{Umkehrschluss von Shannons Kanalcodierungstheorem:}$
| |
| − |
| |
| − | Ist die Rate $R$ des verwendeten $(n$, $k)$–Blockcodes größer als die Kanalkapazität $C$, so ist niemals eine beliebig kleine Blockfehlerwahrscheinlichkeit nicht erreichbar.}}
| |
| − |
| |
| − |
| |
| − | [[Datei:Transinf_9.png|right|frame|Informationsheoretischer Größen für <br>verschiedene $p_{\rm A}$ und $p_{\rm B}= 1- p_{\rm A}$ ]]
| |
| − | {{GraueBox|TEXT=
| |
| − | $\text{Beispiel 4}$: Wir betrachten den gleichen diskreten gedächtnislosen Kanal wie im $\text{Beispiel 2}$.
| |
| − | In diesem $\text{Beispiel 2}$ wurden die Symbolwahrscheinlichkeiten $p_{\rm A} = 0.1$ und $p_{\rm B}= 1- p_{\rm A}=0.9$ vorausgesetzt. Damit ergab sich die Transinformation zu $I(X;Y)= 0.092$ bit/Kanalzugriff ⇒ siehe erste Zeile, vierte Spalte in der Tabelle.
| |
| − |
| |
| − | Die '''Kanalkapazität''' ist die Transinformation $I(X, Y)$ bei bestmöglichen Symbolwahrscheinlichkeiten $p_{\rm A} = 0.55$ und $p_{\rm B}= 1- p_{\rm A}=0.45$:
| |
| − | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = 0.284 \ \rm bit/Kanalzugriff \hspace{0.05cm}.$$
| |
| − |
| |
| − | Aus der Tabelle erkennt man weiter (auf die Zusatzeinheit „bit/Kanalzugriff„ verzichten wir im Folgenden):
| |
| − | *Der Parameter $p_{\rm A} = 0.1$ war sehr ungünstig gewählt, weil beim vorliegenden Kanal das Symbol $\rm A$ mehr verfälscht wird als $\rm B$. Schon mit $p_{\rm A} = 0.9$ ergibt sich ein etwas besserer Wert: $I(X; Y)=0.130$.
| |
| − | *Aus dem gleichen Grund liefert $p_{\rm A} = 0.55$, $p_{\rm B} = 0.45$ ein etwas besseres Ergebnis als gleichwahrscheinliche Symbole $p_{\rm A} = p_{\rm B} =0.5$.
| |
| − | *Je unsymmetrischer der Kanal ist, um so mehr weicht die optimale Wahrscheinlichkeitsfunktion $P_X(X)$ von der Gleichverteilung ab. Im Umkehrschluss: Bei symmetrischem Kanal ergibt sich stets die Gleichverteilung.}}
| |
| − |
| |
| − |
| |
| − | Der Ternärkanal von $\text{Beispiel 3}$ ist symmetrisch. Deshalb ist hier $P_X(X) = \big ( 1/3,\ 1/3,\ 1/3 \big )$ für jeden $q$–Wert optimal, und die in der Ergebnistabelle angegebene Transinformation $I(X;Y)$ ist gleichzeitig die Kanalkapazität $C$.
| |
| − |
| |
| − |
| |
| | | | |
| | | | |
Applet in neuem Tab öffnen
Programmbeschreibung
Theoretischer Hintergrund
Erwartungswerte von 2D–Zufallsgrößen und Korrelationskoeffizient
Wir betrachten eine zweidimensionale $\rm (2D)$–Zufallsgröße $(XY)$ mit der Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ $f_{XY}(x, y)$, wobei zwischen den Einzelkomponenten $X$ und $Y$ statistische Abhängigkeiten bestehen. Ein Sonderfall ist die Korrelation.
$\text{Definition:}$ Unter Korrelation versteht man eine lineare Abhängigkeit zwischen den Einzelkomponenten $X$ und $Y$.
- Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
- Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.
Für das Folgende setzen wir voraus, dass $X$ und $Y$ mittelwertfrei seien ${\rm E}\big [ X \big ] = {\rm E}\big [ Y \big ]=0$. Zur Beschreibung der Korrelation genügen dann folgende Erwartungswerte:
- die Varianzen in $X$– bzw. in $Y$–Richtung:
- $$\sigma_X^2= {\rm E}\big [ X^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}x^2 \cdot f_{X}(x) \, {\rm d}x\hspace{0.05cm},\hspace{0.5cm}\sigma_Y^2= {\rm E}\big [Y^2 \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}y^2 \cdot f_{Y}(y) \, {\rm d}y\hspace{0.05cm};$$
- die Kovarianz zwischen den Einzelkomponenten $X$ und $Y$:
- $$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = \int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\ \cdot y \cdot f_{XY}(x,y) \, {\rm d}x\, {\rm d}y\hspace{0.05cm}.$$
Bei statististischer Unabhängigkeit der beiden Komponenten $X$ und $Y$ ist die Kovarianz $\mu_{XY} \equiv 0$.
- Das Ergebnis $\mu_{XY} = 0$ ist aber auch bei statistisch abhängigen Komponenten $X$ und $Y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind.
- Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $Y=X^2.$
Man spricht von vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen $X$ und $Y$ durch die Gleichung $Y = K · X$ ausgedrückt wird. Dann ergibt sich für die Kovarianz:
- $\mu_{XY} = σ_X · σ_Y$ bei positivem Wert von $K$,
- $\mu_{XY} = -σ_X · σ_Y$ bei negativem $K$–Wert.
Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.
$\text{Definition:}$ Der Korrelationskoeffizient ist der Quotient aus der Kovarianz $\mu_{XY}$ und dem Produkt der Effektivwerte $σ_X$ und $σ_Y$ der beiden Komponenten:
- $$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}.$$
Der Korrelationskoeffizient $\rho_{XY}$ weist folgende Eigenschaften auf:
- Aufgrund der Normierung gilt stets $-1 \le ρ_{XY} ≤ +1$.
- Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{XY} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $X$ und $Y$ ist $ρ_{XY}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $X$–Wert im statistischen Mittel auch $Y$ größer ist als bei kleinerem $X$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $Y$ mit steigendem $X$ im Mittel kleiner wird.
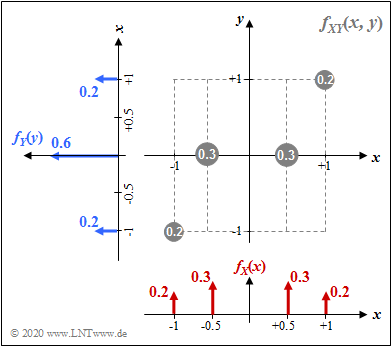
2D-WDF $f_{XY}(x, y)$ sowie die zugehörigen Randwahrscheinlichkeitsdichten $f_{X}(x)$ und $f_{Y}(y)$
$\text{Beispiel 1:}$ Die 2D–Zufallsgröße $XY$ sei diskret und kann nur vier verschiedene Werte annehmen:
- $(+0.5,\ 0)$ sowie $(-0.5,\ 0)$ jeweils mit der Wahrscheinlichkeit $0.3$,
- $(+1,\ +1)$ sowie $(+1,\ -1)$ jeweils mit der Wahrscheinlichkeit $0.2$.
$\rm (A)$ Die Varianzen bzw. die Streuungen können aus $f_{X}(x)$ und $f_{Y}(y)$ berechnet werden:
- $$\sigma_X^2 = 2 \cdot \big [0.2 \cdot 1^2 + 0.3 \cdot 0.5^2 \big] = 0.55\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_X = 0.7416,$$
- $$\sigma_Y^2 = \big [0.2 \cdot (-1)^2 + 0.6 \cdot 0^2 +0.2 \cdot (+1)^2 \big] = 0.4\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\sigma_Y = 0.6324.$$
$\rm (B)$ Für die Kovarianz ergibt sich der folgende Erwartungswert:
- $$\mu_{XY}= {\rm E}\big [ X \cdot Y \big ] = 2 \cdot \big [0.2 \cdot 1 \cdot 1 + 0.3 \cdot 0.5 \cdot 0 \big] = 0.4.$$
$\rm (C)$ Damit erhält man für den Korrelationskoeffizient:
- $$\rho_{XY}=\frac{\mu_{XY} } {\sigma_X \cdot \sigma_Y}=\frac{0.4 } {0.7416 \cdot 0.6324 }\approx 0.853.
$$
Dummy
Korrelationsgerade
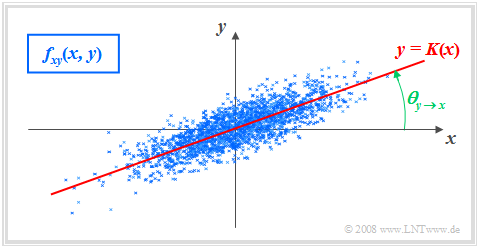
Gaußsche 2D-WDF mit Korrelationsgerade
$\text{Definition:}$ Als Korrelationsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch Regressionsgerade genannt.
Die Korrelationsgerade besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet:
- $$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$
Der Winkel, den die Korrelationsgerade zur $x$–Achse einnimmt, beträgt:
- $$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$
Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt.
- Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.
- Das interaktive Applet Korrelationskoeffizient und Regressionsgerade verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:
- $$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$
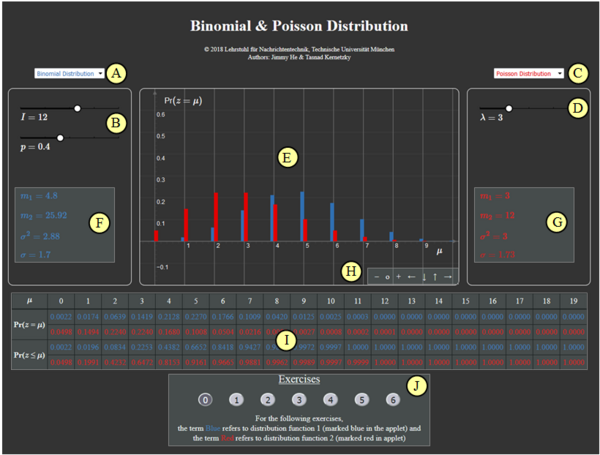
Versuchsdurchführung
- Wählen Sie zunächst die Nummer 1 ... 6 der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Hide solution”.
- Aufgabenstellung und Lösung in Englisch.
Die Nummer 0 entspricht einem „Reset”:
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines „Reset–Textes” mit weiteren Erläuterungen zum Applet.
In der folgenden Beschreibung bedeutet
- Blau: Verteilungsfunktion 1 (im Applet blau markiert),
- Rot: Verteilungsfunktion 2 (im Applet rot markiert).
(1) Setzen Sie Blau: Binomialverteilung $(I=5, \ p=0.4)$ und Rot: Binomialverteilung $(I=10, \ p=0.2)$.
- Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$
$\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$
(2) Es gelten weiter die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder }
{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$.
$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$
$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158.$
(3) Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $
$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$
(4) Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.
- Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;
$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;
(5) Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exakt)}$.
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0 \ ( \approx 0)$
$\hspace{1.85cm} \text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16}/{16!}\approx 2 \cdot 10^{-22}$.
(6) Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$
$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$
Zur Handhabung des Applets
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Applet in neuem Tab öffnen