Kanalcodierung/Decodierung von Faltungscodes: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 20: | Zeile 20: | ||
\underline{x}= (x_1,\hspace{0.05cm} x_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, x_{2L}, \hspace{0.05cm} x_{2L+1} ,\hspace{0.05cm} \text{...} \hspace{0.1cm}, \hspace{0.05cm} x_{2L+2m} ) \hspace{0.05cm}.</math> | \underline{x}= (x_1,\hspace{0.05cm} x_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, x_{2L}, \hspace{0.05cm} x_{2L+1} ,\hspace{0.05cm} \text{...} \hspace{0.1cm}, \hspace{0.05cm} x_{2L+2m} ) \hspace{0.05cm}.</math> | ||
| − | *Die Empfangssequenz $\underline{y} = (y_1, \ y_2, \ \text{...} )$ ergibt sich entsprechend dem angenommenen Kanalmodell. Bei einem digitalen Modell wie dem [[Kanalcodierung/ | + | *Die Empfangssequenz $\underline{y} = (y_1, \ y_2, \ \text{...} )$ ergibt sich entsprechend dem angenommenen Kanalmodell. Bei einem digitalen Modell wie dem [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| Binary Symmetric Channel]] (BSC) gilt $y_i ∈ \{0, 1\}$, so dass die Verfälschung von $\underline{x}$ auf $\underline{y}$ mit der [[Kanalcodierung/Zielsetzung_der_Kanalcodierung#Einige_wichtige_Definitionen_zur_Blockcodierung| Hamming–Distanz]] $d_{\rm H}(\underline{x}, \underline{y})$ quantifiziert werden kann. Die erforderlichen Modifikationen für den [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#AWGN.E2.80.93Kanal_bei_bin.C3.A4rem_Eingang| AWGN–Kanal]] folgen im Abschnitt [[Kanalcodierung/Decodierung_von_Faltungscodes#Viterbi.E2.80.93Algorithmus.2C_basierend_auf_Korrelation_und_Metriken| Viterbi–Algorithmus, basierend auf Korrelation und Metriken]]. |
*Der Viterbi–Algorithmus liefert eine Schätzung $\underline{z}$ für die Codesequenz $\underline{x}$ und eine weitere Schätzung $\underline{v}$ für die Informationssequenz $\underline{u}$. Dabei gilt: | *Der Viterbi–Algorithmus liefert eine Schätzung $\underline{z}$ für die Codesequenz $\underline{x}$ und eine weitere Schätzung $\underline{v}$ für die Informationssequenz $\underline{u}$. Dabei gilt: | ||
| Zeile 183: | Zeile 183: | ||
== Zusammenhang zwischen Hamming–Distanz und Korrelation == | == Zusammenhang zwischen Hamming–Distanz und Korrelation == | ||
<br> | <br> | ||
| − | Insbesondere beim [[Kanalcodierung/ | + | Insbesondere beim [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC| BSC–Modell]] – aber auch bei jedem anderen Binärkanal ⇒ Eingang $x_i ∈ \{0,1\}$, Ausgang $y_i ∈ \{0,1\}$ wie zum Beispiel dem [[Digitalsignalübertragung/Bündelfehlerkanäle#Kanalmodell_nach_Gilbert.E2.80.93Elliott| Gilbert–Elliott–Modell]] – liefert die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{y})$ genau die gleiche Information über die Ähnlichkeit der Eingangsfolge $\underline{x}$ und der Ausgangsfolge $\underline{y}$ wie das [[Digitalsignalübertragung/Signale,_Basisfunktionen_und_Vektorräume#Zur_Nomenklatur_im_vierten_Kapitel| innere Produkt]]. Nimmt man an, dass die beiden Folgen in bipolarer Darstellung vorliegen (gekennzeichnet durch Tilden) und dass die Folgenlänge jeweils $L$ ist, so gilt für das innere Produkt: |
::<math><\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} | ::<math><\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} | ||
= \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.</math> | = \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.</math> | ||
| − | Wir bezeichnen dieses innere Produkt manchmal auch als den & | + | Wir bezeichnen dieses innere Produkt manchmal auch als den "'''Korrelationswert'''". Im Unterschied zum [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgr%C3%B6%C3%9Fen#Korrelationskoeffizient| Korrelationskoeffizienten]] kann der Korrelationswert den Wertebereich $±1$ durchaus überschreiten.<br> |
| − | [[Datei:KC_T_3_4_S5_neu.png|right|frame|Zusammenhang zwischen Haming–Distanz und | + | [[Datei:KC_T_3_4_S5_neu.png|right|frame|Zusammenhang zwischen Haming–Distanz und Korrelationswert |class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.<br> | $\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.<br> | ||
| Zeile 255: | Zeile 255: | ||
$\text{Beispiel 5:}$ Die folgende Detailbeschreibung der Trellisauswertung beziehen sich auf das obige Trellis: | $\text{Beispiel 5:}$ Die folgende Detailbeschreibung der Trellisauswertung beziehen sich auf das obige Trellis: | ||
| − | *Die Metriken zum Zeitpunkt $i = 1$ ergeben sich mit $\underline{y}_1 = (11)$ zu | + | *Die Metriken zum Zeitpunkt $i = 1$ ergeben sich mit $\underline{y}_1 = (11)$ zu |
::<math>{\it \Lambda}_1(S_0) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} | ::<math>{\it \Lambda}_1(S_0) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} | ||
| Zeile 264: | Zeile 264: | ||
= \hspace{0.1cm} +2 \hspace{0.05cm}.</math> | = \hspace{0.1cm} +2 \hspace{0.05cm}.</math> | ||
| − | *Entsprechend gilt zum Zeitpunkt $i = 2$ mit $\underline{y}_2 = (11)$: | + | *Entsprechend gilt zum Zeitpunkt $i = 2$ mit $\underline{y}_2 = (11)$: |
::<math>{\it \Lambda}_2(S_0) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} | ::<math>{\it \Lambda}_2(S_0) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} | ||
| Zeile 275: | Zeile 275: | ||
= \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm}.</math> | = \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm}.</math> | ||
| − | *Ab dem Zeitpunkt $i =3$ muss eine Entscheidung zwischen zwei Metriken getroffen werden. Beispielsweise erhält man mit $\underline{y}_3 = (10)$ für die oberste und die unterste Metrik im Trellis: | + | *Ab dem Zeitpunkt $i =3$ muss eine Entscheidung zwischen zwei Metriken getroffen werden. Beispielsweise erhält man mit $\underline{y}_3 = (10)$ für die oberste und die unterste Metrik im Trellis: |
::<math>{\it \Lambda}_3(S_0)={\rm max} \left [{\it \Lambda}_{2}(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}> \right ] = {\rm max} \left [ -4+0\hspace{0.05cm},\hspace{0.05cm} +2+0 \right ] = +2\hspace{0.05cm},</math> | ::<math>{\it \Lambda}_3(S_0)={\rm max} \left [{\it \Lambda}_{2}(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}> \right ] = {\rm max} \left [ -4+0\hspace{0.05cm},\hspace{0.05cm} +2+0 \right ] = +2\hspace{0.05cm},</math> | ||
::<math>{\it \Lambda}_3(S_3) ={\rm max} \left [{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_3) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}> \right ] = {\rm max} \left [ 0+0\hspace{0.05cm},\hspace{0.05cm} +2+2 \right ] = +4\hspace{0.05cm}.</math> | ::<math>{\it \Lambda}_3(S_3) ={\rm max} \left [{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_3) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}> \right ] = {\rm max} \left [ 0+0\hspace{0.05cm},\hspace{0.05cm} +2+2 \right ] = +4\hspace{0.05cm}.</math> | ||
| − | Vergleicht man die zu zu maximierenden Metriken ${\it \Lambda}_i(S_{\mu})$ mit den zu minimierenden Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ gemäß [[Kanalcodierung/Decodierung_von_Faltungscodes#Decodierbeispiele_f.C3.BCr_den_fehlerbehafteten_Fall| Beispiel 1]], so erkennt man den folgenden deterministischen Zusammenhang: | + | Vergleicht man die zu zu maximierenden Metriken ${\it \Lambda}_i(S_{\mu})$ mit den zu minimierenden Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ gemäß dem [[Kanalcodierung/Decodierung_von_Faltungscodes#Decodierbeispiele_f.C3.BCr_den_fehlerbehafteten_Fall| $\text{Beispiel 1}$]], so erkennt man den folgenden deterministischen Zusammenhang: |
::<math>{\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [ i - {\it \Gamma}_i(S_{\mu}) \big ] \hspace{0.05cm}.</math> | ::<math>{\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [ i - {\it \Gamma}_i(S_{\mu}) \big ] \hspace{0.05cm}.</math> | ||
| Zeile 289: | Zeile 289: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
| − | *Beim Binärkanal – zum Beispiel nach dem BSC–Modell – führen die beiden beschriebenen Viterbi–Varianten | + | *Beim Binärkanal – zum Beispiel nach dem BSC–Modell – führen die beiden beschriebenen Viterbi–Varianten „Fehlergrößenminimierung” und „Metrikmaximierung” zum gleichen Ergebnis.<br> |
| − | *Beim AWGN–Kanal ist dagegen die Fehlergrößenminimierung nicht anwendbar, da keine Hamming–Distanz zwischen dem binären Eingang $\underline{x}$ und dem analogen Ausgang $\underline{y}$ angegeben werden kann.<br> | + | *Beim AWGN–Kanal ist dagegen die Fehlergrößenminimierung nicht anwendbar, da keine Hamming–Distanz zwischen dem binären Eingang $\underline{x}$ und dem analogen Ausgang $\underline{y}$ angegeben werden kann.<br> |
| − | *Die Metrikmaximierung ist beim AWGN–Kanal vielmehr identisch mit der Minimierung der [[Kanalcodierung/Klassifizierung_von_Signalen#ML.E2.80.93Entscheidung_beim_AWGN.E2.80.93Kanal| Euklidischen Distanz]] – siehe [[Aufgaben:Aufgabe_3.10Z:_ML–Decodierung_von_Faltungscodes|Aufgabe 3.10Z]].<br> | + | *Die Metrikmaximierung ist beim AWGN–Kanal vielmehr identisch mit der Minimierung der [[Kanalcodierung/Klassifizierung_von_Signalen#ML.E2.80.93Entscheidung_beim_AWGN.E2.80.93Kanal| Euklidischen Distanz]] – siehe [[Aufgaben:Aufgabe_3.10Z:_ML–Decodierung_von_Faltungscodes|Aufgabe 3.10Z]].<br> |
| − | *Ein weiterer Vorteil der Metrikmaximierung ist, dass eine Zuverlässigkeitsinformation über die Empfangswerte $\underline{y}$ in einfacher Weise berücksichtigt werden kann.}}<br> | + | *Ein weiterer Vorteil der Metrikmaximierung ist, dass eine Zuverlässigkeitsinformation über die Empfangswerte $\underline{y}$ in einfacher Weise berücksichtigt werden kann.}}<br> |
== Viterbi–Entscheidung bei nicht–terminierten Faltungscodes== | == Viterbi–Entscheidung bei nicht–terminierten Faltungscodes== | ||
<br> | <br> | ||
| − | Bisher wurde stets ein terminierter Faltungscode der Länge $L\hspace{0.05cm}' = L + m$ betrachtet, und das Ergebnis des Viterbi–Decoders war der durchgehende Trellispfad vom Startzeitpunkt $(i = 0)$ bis zum Ende $(i = L\hspace{0.05cm}')$.<br> | + | Bisher wurde stets ein terminierter Faltungscode der Länge $L\hspace{0.05cm}' = L + m$ betrachtet, und das Ergebnis des Viterbi–Decoders war der durchgehende Trellispfad vom Startzeitpunkt $(i = 0)$ bis zum Ende $(i = L\hspace{0.05cm}')$.<br> |
| − | *Bei nicht–terminierten Faltungscodes $(L\hspace{0.05cm}' → ∞)$ ist diese Entscheidungsstrategie nicht anwendbar. | + | *Bei nicht–terminierten Faltungscodes $(L\hspace{0.05cm}' → ∞)$ ist diese Entscheidungsstrategie nicht anwendbar. |
*Hier muss der Algorithmus abgewandelt werden, um in endlicher Zeit eine bestmögliche Schätzung (gemäß Maximum–Likelihood) der einlaufenden Bits der Codesequenz liefern zu können.<br> | *Hier muss der Algorithmus abgewandelt werden, um in endlicher Zeit eine bestmögliche Schätzung (gemäß Maximum–Likelihood) der einlaufenden Bits der Codesequenz liefern zu können.<br> | ||
| Zeile 309: | Zeile 309: | ||
*die Nullfolge ⇒ $\underline{u} = \underline{0} = (0, 0, 0, \ \text{...})$ ⇒ $\underline{x} = \underline{0} = (00, 00, 00, \ \text{...})$,<br> | *die Nullfolge ⇒ $\underline{u} = \underline{0} = (0, 0, 0, \ \text{...})$ ⇒ $\underline{x} = \underline{0} = (00, 00, 00, \ \text{...})$,<br> | ||
| − | *jeweils einen Übertragungsfehler bei $i = 4$ und $i = 5$.<br><br> | + | *jeweils einen Übertragungsfehler bei $i = 4$ und $i = 5$.<br><br> |
Anhand der Stricharten erkennt man erlaubte (durchgezogene) und verbotene (punktierte) Pfeile in rot $(u_i = 0)$ und blau $(u_i = 1)$. Punktierte Linien haben einen Vergleich gegen einen Konkurrenten verloren und können nicht Teil des ausgewählten Pfades sein.<br> | Anhand der Stricharten erkennt man erlaubte (durchgezogene) und verbotene (punktierte) Pfeile in rot $(u_i = 0)$ und blau $(u_i = 1)$. Punktierte Linien haben einen Vergleich gegen einen Konkurrenten verloren und können nicht Teil des ausgewählten Pfades sein.<br> | ||
| Zeile 315: | Zeile 315: | ||
[[Datei:P ID2676 KC T 3 4 S7 v1.png|center|frame|Beispielhaftes Trellis und überlebende Pfade|class=fit]] | [[Datei:P ID2676 KC T 3 4 S7 v1.png|center|frame|Beispielhaftes Trellis und überlebende Pfade|class=fit]] | ||
| − | Der untere Teil der Grafik zeigt die $2^m$ überlebenden Pfade ${\it \Phi}_9(S_{\mu})$ zum Zeitpunkt $i = 9$. | + | Der untere Teil der Grafik zeigt die $2^m = 4$ überlebenden Pfade ${\it \Phi}_9(S_{\mu})$ zum Zeitpunkt $i = 9$. |
| − | *Man findet diese Pfade am einfachsten von rechts nach links ( | + | *Man findet diese Pfade am einfachsten von rechts nach links (Rückwärtsrichtung). |
| − | *Die folgende Angabe zeigt die durchlaufenen Zustände $S_{\mu}$ allerdings in Vorwärtsrichtung:<br> | + | *Die folgende Angabe zeigt die durchlaufenen Zustände $S_{\mu}$ allerdings in Vorwärtsrichtung:<br> |
:$${\it \Phi}_9(S_0) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0,$$ | :$${\it \Phi}_9(S_0) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0,$$ | ||
:$${\it \Phi}_9(S_1) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_3 → S_2 → S_1,$$ | :$${\it \Phi}_9(S_1) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_3 → S_2 → S_1,$$ | ||
| Zeile 323: | Zeile 323: | ||
:$${\it \Phi}_9(S_3) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_3.$$ | :$${\it \Phi}_9(S_3) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_3.$$ | ||
| − | Zu früheren Zeitpunkten $(i<9)$ würden sich andere überlebende Pfade ${\it \Phi}_i(S_{\mu})$ ergeben. Deshalb definieren wir: | + | Zu früheren Zeitpunkten $(i<9)$ würden sich andere überlebende Pfade ${\it \Phi}_i(S_{\mu})$ ergeben. Deshalb definieren wir: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Der <b>überlebende Pfad</b> (englisch: <i>Survivor</i>) ${\it \Phi}_i(S_{\mu})$ ist der durchgehende Pfad vom Start $S_0$ (bei $i = 0$ | + | $\text{Definition:}$ Der <b>überlebende Pfad</b> (englisch: <i>Survivor</i>) ${\it \Phi}_i(S_{\mu})$ ist der durchgehende Pfad vom Start $S_0$ $($bei $i = 0)$ zum Knoten $S_{\mu}$ zum Zeitpunkt $i$. Empfehlenswert ist die Pfadsuche in Rückwärtsrichtung.}}<br> |
| − | Die folgende Grafik zeigt die überlebenden Pfade für die Zeitpunkte $i = 6$ bis $i = 9$. Zusätzlich sind die jeweiligen Metriken ${\it \Lambda}_i(S_{\mu})$ für alle vier Zustände angegeben. | + | Die folgende Grafik zeigt die überlebenden Pfade für die Zeitpunkte $i = 6$ bis $i = 9$. Zusätzlich sind die jeweiligen Metriken ${\it \Lambda}_i(S_{\mu})$ für alle vier Zustände angegeben. |
| − | [[Datei:P ID2677 KC T 3 4 S7b v1.png|center|frame|Die überlebenden Pfade ${\it \Phi}_6, \ \text{...} \ , \ {\it \Phi}_9$|class=fit]] | + | [[Datei:P ID2677 KC T 3 4 S7b v1.png|center|frame|Die überlebenden Pfade ${\it \Phi}_6, \ \text{...} \ , \ {\it \Phi}_9$|class=fit]] |
Diese Grafik ist wie folgt zu interpretieren: | Diese Grafik ist wie folgt zu interpretieren: | ||
| − | *Zum Zeitpunkt $i = 9$ kann noch keine endgültige ML–Entscheidung über die ersten neun Bit der Informationssequenz getroffen werden. Allerdings ist bereits sicher, dass die wahrscheinlichste Bitfolge durch einen der Pfade ${\it \Phi}_9(S_0), \ \text{...} \ , \ {\it \Phi}_9(S_3)$ richtig wiedergegeben wird.<br> | + | *Zum Zeitpunkt $i = 9$ kann noch keine endgültige ML–Entscheidung über die ersten neun Bit der Informationssequenz getroffen werden. Allerdings ist bereits sicher, dass die wahrscheinlichste Bitfolge durch einen der Pfade ${\it \Phi}_9(S_0), \ \text{...} \ , \ {\it \Phi}_9(S_3)$ richtig wiedergegeben wird.<br> |
| − | *Da alle vier Pfade | + | *Da alle vier Pfade bis $i = 3$ identisch sind, ist die Entscheidung „$v_1 = 0, v_2 = 0, \ v_3 = 0$” die bestmögliche (hellgraue Hinterlegung). Auch zu einem späteren Zeitpunkt würde keine andere Entscheidung getroffen werden. Hinsichtlich der Bits $v_4, \ v_5, \ \text{...}$ sollte man sich zu diesem frühen Zeitpunkt noch nicht festlegen.<br> |
| − | *Müsste man zum Zeitpunkt $i = 9$ eine Zwangsentscheidung treffen, so würde man sich für ${\it \Phi}_9(S_0)$ ⇒ $\underline{v} = (0, 0, \ \text{...} \ , 0)$ entscheiden, da die Metrik ${\it \Lambda}_9(S_0) = 14$ größer ist als die Vergleichsmetriken.<br> | + | *Müsste man zum Zeitpunkt $i = 9$ eine Zwangsentscheidung treffen, so würde man sich für ${\it \Phi}_9(S_0)$ ⇒ $\underline{v} = (0, 0, \ \text{...} \ , 0)$ entscheiden, da die Metrik ${\it \Lambda}_9(S_0) = 14$ größer ist als die Vergleichsmetriken.<br> |
| − | *Die Zwangsentscheidung zum Zeitpunkt $i = 9$ führt in diesem Beispiel zum richtigen Ergebnis. Zum Zeitpunkt $i = 6$ wäre ein solcher Zwangsentscheid falsch gewesen ⇒ $\underline{v} = (0, 0, 0, 1, 0, 1)$, und zu den Zeitpunten $i = 7$ bzw. $i = 8$ nicht eindeutig.<br> | + | *Die Zwangsentscheidung zum Zeitpunkt $i = 9$ führt in diesem Beispiel zum richtigen Ergebnis. Zum Zeitpunkt $i = 6$ wäre ein solcher Zwangsentscheid falsch gewesen ⇒ $\underline{v} = (0, 0, 0, 1, 0, 1)$, und zu den Zeitpunten $i = 7$ bzw. $i = 8$ nicht eindeutig.<br> |
| Zeile 345: | Zeile 345: | ||
== Weitere Decodierverfahren für Faltungscodes == | == Weitere Decodierverfahren für Faltungscodes == | ||
<br> | <br> | ||
| − | Wir haben uns bisher nur mit dem Viterbi–Algorithmus in der Form beschäftigt, der 1967 von Andrew J. Viterbi in [Vit67]<ref name'Vit67'>Viterbi, A.J.: ''Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm''. In: IEEE Transactions on Information Theory, vol. IT-13, pp. 260-269, April 1967.</ref> veröffentlicht wurde. Erst 1974 hat [https://de.wikipedia.org/wiki/David_Forney George David Forney] nachgewiesen, dass dieser Algorithmus eine Maximum–Likelihood–Decodierung von Faltungscodes durchführt.<br> | + | Wir haben uns bisher nur mit dem Viterbi–Algorithmus in der Form beschäftigt, der 1967 von Andrew J. Viterbi in [Vit67]<ref name'Vit67'>Viterbi, A.J.: ''Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm''. In: IEEE Transactions on Information Theory, vol. IT-13, pp. 260-269, April 1967.</ref> veröffentlicht wurde. Erst 1974 hat [https://de.wikipedia.org/wiki/David_Forney George David Forney] nachgewiesen, dass dieser Algorithmus eine Maximum–Likelihood–Decodierung von Faltungscodes durchführt.<br> |
| − | Aber schon in den Jahren zuvor waren viele Wissenschaftler sehr bemüht, effiziente Decodierverfahren für die 1955 erstmals von [https://de.wikipedia.org/wiki/Peter_Elias Peter Elias] beschriebenen Faltungscodes bereitzustellen. Zu nennen sind hier unter Anderem – genauere Beschreibungen findet man beispielsweise in [Bos98]<ref name='Bos98'>Bossert, M.: ''Kanalcodierung.'' Stuttgart: B. G. Teubner, 1998.</ref> oder der englischen Ausgabe [Bos99]<ref name='Bos99'>Bossert, M.: ''Channel Coding for Telecommunications.'' Wiley & Sons, 1999.</ref>. | + | Aber schon in den Jahren zuvor waren viele Wissenschaftler sehr bemüht, effiziente Decodierverfahren für die 1955 erstmals von [https://de.wikipedia.org/wiki/Peter_Elias Peter Elias] beschriebenen Faltungscodes bereitzustellen. Zu nennen sind hier unter Anderem – genauere Beschreibungen findet man beispielsweise in [Bos98]<ref name='Bos98'>Bossert, M.: ''Kanalcodierung.'' Stuttgart: B. G. Teubner, 1998.</ref> oder der englischen Ausgabe [Bos99]<ref name='Bos99'>Bossert, M.: ''Channel Coding for Telecommunications.'' Wiley & Sons, 1999.</ref>. |
| − | *[http://ieeexplore.ieee.org/document/1057663/ <i>Sequential Decoding</i> ] von J. M. Wozencraft und B. Reiffen aus dem Jahre 1961,<br> | + | *[http://ieeexplore.ieee.org/document/1057663/ <i>Sequential Decoding</i> ] von J. M. Wozencraft und B. Reiffen aus dem Jahre 1961,<br> |
| − | *der Vorschlag von [https://en.wikipedia.org/wiki/Robert_Fano Robert Mario Fano] (1963), der als <i>Fano–Algorithmus</i> bekannt wurde,<br> | + | *der Vorschlag von [https://en.wikipedia.org/wiki/Robert_Fano Robert Mario Fano] (1963), der als <i>Fano–Algorithmus</i> bekannt wurde,<br> |
| − | *die Arbeiten von Kamil Zigangirov (1966) und [https://en.wikipedia.org/wiki/Frederick_Jelinek Frederick Jelinek] (1969), deren Decodierverfahren als <i>Stack–Algorithmus</i> bezeichnet wird.<br><br> | + | *die Arbeiten von Kamil Zigangirov (1966) und [https://en.wikipedia.org/wiki/Frederick_Jelinek Frederick Jelinek] (1969), deren Decodierverfahren auch als <i>Stack–Algorithmus</i> bezeichnet wird.<br><br> |
Alle diese Decodierverfahren und auch der Viterbi–Algorithmus in seiner bisher beschriebenen Form liefern „hart” entschiedene Ausgangswerte ⇒ $v_i ∈ \{0, 1\}$. Oftmals wären jedoch Informationen über die Zuverlässigkeit der getroffenen Entscheidungen wünschenswert, insbesondere dann, wenn ein verkettetes Codierschema mit einem äußeren und einem inneren Code vorliegt.<br> | Alle diese Decodierverfahren und auch der Viterbi–Algorithmus in seiner bisher beschriebenen Form liefern „hart” entschiedene Ausgangswerte ⇒ $v_i ∈ \{0, 1\}$. Oftmals wären jedoch Informationen über die Zuverlässigkeit der getroffenen Entscheidungen wünschenswert, insbesondere dann, wenn ein verkettetes Codierschema mit einem äußeren und einem inneren Code vorliegt.<br> | ||
| − | Kennt man die Zuverlässigkeit der vom inneren Decoder entschiedenen Bits zumindest grob, so kann durch diese Information die Bitfehlerwahrscheinlichkeit des äußeren Decoders (signifikant) herabgesetzt werden. Der von [[Biografien_und_Bibliografien/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29|Joachim Hagenauer]] in [Hag90]<ref name='Hag90'>Hagenauer, J.: ''Soft Output Viterbi Decoder.'' In: Technischer Report, Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), 1990.</ref> vorgeschlagene <i>Soft–Output–Viterbi–Algorithmus</i> (SOVA) erlaubt es, zusätzlich zu den entschiedenen Symbolen auch jeweils ein Zuverlässigkeitsmaß anzugeben.<br> | + | Kennt man die Zuverlässigkeit der vom inneren Decoder entschiedenen Bits zumindest grob, so kann durch diese Information die Bitfehlerwahrscheinlichkeit des äußeren Decoders (signifikant) herabgesetzt werden. Der von [[Biografien_und_Bibliografien/Lehrstuhlinhaber_des_LNT#Prof._Dr.-Ing._Dr.-Ing._E.h._Joachim_Hagenauer_.281993-2006.29|Joachim Hagenauer]] in [Hag90]<ref name='Hag90'>Hagenauer, J.: ''Soft Output Viterbi Decoder.'' In: Technischer Report, Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), 1990.</ref> vorgeschlagene <i>Soft–Output–Viterbi–Algorithmus</i> (SOVA) erlaubt es, zusätzlich zu den entschiedenen Symbolen auch jeweils ein Zuverlässigkeitsmaß anzugeben.<br> |
| + | |||
| + | Abschließend gehen wir noch etwas genauer auf den <i>BCJR–Algorithmus</i> ein, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv [BCJR74]<ref name='BCJR74'>Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: ''Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate.'' In: IEEE Transactions on Information Theory, Vol. IT-20, S. 284-287, 1974.</ref>. | ||
| + | *Während der Viterbi–Algorithmus nur eine Schätzung der Gesamtsequenz vornimmt ⇒ [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Definitionen_der_verschiedenen_Optimalempf.C3.A4nger|''block–wise ML'']], schätzt der BCJR–Algorithmus ein einzelnes Symbol (Bit) unter Berücksichtigung der gesamten empfangenen Codesequenz. | ||
| + | * Es handelt sich hierbei also um eine <i>symbolweise Maximum–Aposteriori–Decodierung</i> ⇒ [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Definitionen_der_verschiedenen_Optimalempf.C3.A4nger|''bit–wise MAP'']].<br> | ||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ Der Unterschied zwischen Viterbi–Algorithmus und BCJR–Algorithmus soll – stark vereinfacht – am Beispiel eines terminierten Faltungscodes dargestellt werden: | $\text{Fazit:}$ Der Unterschied zwischen Viterbi–Algorithmus und BCJR–Algorithmus soll – stark vereinfacht – am Beispiel eines terminierten Faltungscodes dargestellt werden: | ||
| − | *Der <b>Viterbi–Algorithmus</b> arbeitet das Trellis nur in einer Richtung – der <i>Vorwärtsrichtung</i> – ab und berechnet für jeden Knoten die Metriken ${\it \Lambda}_i(S_{\mu})$. Nach Erreichen des Endknotens wird der überlebende Pfad gesucht, der die wahrscheinlichste Codesequenz kennzeichnet.<br> | + | *Der <b>Viterbi–Algorithmus</b> arbeitet das Trellis nur in einer Richtung – der <i>Vorwärtsrichtung</i> – ab und berechnet für jeden Knoten die Metriken ${\it \Lambda}_i(S_{\mu})$. Nach Erreichen des Endknotens wird der überlebende Pfad gesucht, der die wahrscheinlichste Codesequenz kennzeichnet.<br> |
| − | *Beim <b>BCJR–Algorithmus</b> wird das Trellis zweimal abgearbeitet, einmal in Vorwärtsrichtung und anschließend in <i>Rückwärtsrichtung</i>. Für jeden Knoten sind dann zwei Metriken angebbar, aus denen für jedes Bit die Aposterori–Wahrscheinlichkeit bestimmt werden kann.}}<br> | + | *Beim <b>BCJR–Algorithmus</b> wird das Trellis zweimal abgearbeitet, einmal in Vorwärtsrichtung und anschließend in <i>Rückwärtsrichtung</i>. Für jeden Knoten sind dann zwei Metriken angebbar, aus denen für jedes Bit die Aposterori–Wahrscheinlichkeit bestimmt werden kann.}}<br> |
<i>Hinweise:</i> | <i>Hinweise:</i> | ||
| − | *Diese Kurzzusammenfassung basiert auf dem Lehrbüchern [Bos98]<ref name='Bos98'>Bossert, M.: ''Kanalcodierung.'' Stuttgart: B. G. Teubner, 1998.</ref> bzw. [Bos99]<ref name='Bos99'>Bossert, M.: ''Channel Coding for Telecommunications.'' Wiley & Sons, 1999.</ref>. | + | *Diese Kurzzusammenfassung basiert auf dem Lehrbüchern [Bos98]<ref name='Bos98'>Bossert, M.: ''Kanalcodierung.'' Stuttgart: B. G. Teubner, 1998.</ref> bzw. [Bos99]<ref name='Bos99'>Bossert, M.: ''Channel Coding for Telecommunications.'' Wiley & Sons, 1999.</ref>. |
| − | *Eine etwas ausführlichere Beschreibung des BCJR–Algorithmus' folgt auf der Seite [[Kanalcodierung/Soft–in_Soft–out_Decoder#Hard_Decision_vs._Soft_Decision| Hard Decision vs. Soft Decision]] im vierten Hauptkapitel.<br> | + | *Eine etwas ausführlichere Beschreibung des BCJR–Algorithmus' folgt auf der Seite [[Kanalcodierung/Soft–in_Soft–out_Decoder#Hard_Decision_vs._Soft_Decision| Hard Decision vs. Soft Decision]] [https://www.lntwww.de/Kanalcodierung im vierten Hauptkapitel] „Iterative Decodierverfahren”.<br> |
Aktuelle Version vom 17. November 2022, 18:50 Uhr
Inhaltsverzeichnis
- 1 Blockschaltbild und Voraussetzungen
- 2 Vorbemerkungen zu den nachfolgenden Decodierbeispielen
- 3 Erstellen des Trellis im fehlerfreien Fall – Fehlergrößenberechnung
- 4 Auswerten des Trellis im fehlerfreien Fall – Pfadsuche
- 5 Decodierbeispiele für den fehlerbehafteten Fall
- 6 Zusammenhang zwischen Hamming–Distanz und Korrelation
- 7 Viterbi–Algorithmus, basierend auf Korrelation und Metriken
- 8 Viterbi–Entscheidung bei nicht–terminierten Faltungscodes
- 9 Weitere Decodierverfahren für Faltungscodes
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Blockschaltbild und Voraussetzungen
Ein wesentlicher Vorteil der Faltungscodierung ist, dass es hierfür mit dem Viterbi–Algorithmus ein sehr effizientes Decodierverfahren gibt. Dieser von Andrew James Viterbi entwickelte Algorithmus wurde bereits im Kapitel Viterbi–Empfänger des Buches „Digitalsignalübertragung” im Hinblick auf seinen Einsatz zur Entzerrung beschrieben.
Für seinen Einsatz als Faltungsdecodierer gehen wir von obigem Blockschaltbild und den folgenden Voraussetzungen aus:
- Die Informationssequenz $\underline{u} = (u_1, \ u_2, \ \text{...} \ )$ ist hier im Gegensatz zur Beschreibung der linearen Blockcodes ⇒ Erstes Hauptkapitel oder von Reed–Solomon–Codes ⇒ Zweites Hauptkapitel im allgemeinen unendlich lang („semi–infinite” ). Für die Informationssymbole gilt stets $u_i ∈ \{0, 1\}$.
- Die Codesequenz $\underline{x} = (x_1, \ x_2, \ \text{...})$ mit $x_i ∈ \{0, 1\}$ hängt außer von $\underline{u}$ auch von der Coderate $R = 1/n$, dem Gedächtnis $m$ und der Übertragungsfunktionsmatrix $\mathbf{G}(D)$ ab. Bei endlicher Anzahl $L$ an Informationsbits sollte der Faltungscode durch Anfügen von $m$ Nullen terminiert werden:
- \[\underline{u}= (u_1,\hspace{0.05cm} u_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, u_L, \hspace{0.05cm} 0 \hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.1cm}, 0 ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (x_1,\hspace{0.05cm} x_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, x_{2L}, \hspace{0.05cm} x_{2L+1} ,\hspace{0.05cm} \text{...} \hspace{0.1cm}, \hspace{0.05cm} x_{2L+2m} ) \hspace{0.05cm}.\]
- Die Empfangssequenz $\underline{y} = (y_1, \ y_2, \ \text{...} )$ ergibt sich entsprechend dem angenommenen Kanalmodell. Bei einem digitalen Modell wie dem Binary Symmetric Channel (BSC) gilt $y_i ∈ \{0, 1\}$, so dass die Verfälschung von $\underline{x}$ auf $\underline{y}$ mit der Hamming–Distanz $d_{\rm H}(\underline{x}, \underline{y})$ quantifiziert werden kann. Die erforderlichen Modifikationen für den AWGN–Kanal folgen im Abschnitt Viterbi–Algorithmus, basierend auf Korrelation und Metriken.
- Der Viterbi–Algorithmus liefert eine Schätzung $\underline{z}$ für die Codesequenz $\underline{x}$ und eine weitere Schätzung $\underline{v}$ für die Informationssequenz $\underline{u}$. Dabei gilt:
- \[{\rm Pr}(\underline{z} \ne \underline{x})\stackrel{!}{=}{\rm Minimum} \hspace{0.25cm}\Rightarrow \hspace{0.25cm} {\rm Pr}(\underline{\upsilon} \ne \underline{u})\stackrel{!}{=}{\rm Minimum} \hspace{0.05cm}.\]
$\text{Fazit:}$ Bei einem digitalen Kanalmodell (zum Beispiel dem BSC–Modell) sucht der Viterbi–Algorithmus von allen möglichen Codesequenzen $\underline{x}\hspace{0.05cm}'$ diejenige Sequenz $\underline{z}$ mit der minimalen Hamming–Distanz $d_{\rm H}(\underline{x}\hspace{0.05cm}', \underline{y})$ zur Empfangssequenz $\underline{y}$:
\[\underline{z} = {\rm arg} \min_{\underline{x}\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}( \underline{x}\hspace{0.05cm}'\hspace{0.02cm},\hspace{0.02cm} \underline{y} ) = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm} \vert \hspace{0.05cm} \underline{x}')\hspace{0.05cm}.\]
Das bedeutet auch: Der Viterbi–Algorithmus erfüllt das Maximum–Likelihood–Kriterium.
Vorbemerkungen zu den nachfolgenden Decodierbeispielen
Für alle Beispiele in diesem Kapitels gelten folgende Voraussetzungen:
- Standard–Faltungscodierer: Rate $R = 1/2$, Gedächtnis $m = 2$;
- Übertragungsfunktionsmatrix: $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$;
- Länge der Informationssequenz: $L = 5$;
- Berücksichtigung der Terminierung: $L\hspace{0.05cm}' = 7$;
- Länge der Sequenzen $\underline{x}$ und $\underline{y}$ : jeweils $14$ Bit;
- Aufteilung gemäß $\underline{y} = (\underline{y}_1, \ \underline{y}_2, \ \text{...} \ , \ \underline{y}_7)$
⇒ Bitpaare $\underline{y}_i ∈ \{00, 01, 10, 11\}$; - Viterbi–Decodierung mittels Trellisdiagramms:
- roter Pfeil ⇒ Hypothese $u_i = 0$,
- blauer Pfeil ⇒ Hypothese $u_i = 1$;
- hypothetische Codesequenz $\underline{x}_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$;
- alle hypothetischen Größen mit Apostroph.
Wir gehen stets davon aus, dass die Viterbi–Decodierung auf der Hamming–Distanz $d_{\rm H}(\underline{x}_i\hspace{0.01cm}', \ \underline{y}_i)$ zwischen dem Empfangswort $\underline{y}_i$ und den vier möglichen Codeworten $x_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$ basiert. Dann gehen wir wie folgt vor:
- In die noch leeren Kreise werden die Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ der Zustände $S_{\mu} (0 ≤ \mu ≤ 3)$ zu den Zeitpunkten $i$ eingetragen. Der Startwert ist stets ${\it \Gamma}_0(S_0) = 0$.
- Die Fehlergrößen für $i = 1$ und $i = 2$ ergeben sich zu
- \[{\it \Gamma}_1(S_0) =d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm}, \hspace{2.38cm}{\it \Gamma}_1(S_1) = d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_0) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_1) = {\it \Gamma}_1(S_0)+ d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm},\hspace{0.6cm}{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1)+ d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm}.\]
- Ab $i = 3$ hat das Trellis seine Grundform erreicht, und zur Berechnung aller ${\it \Gamma}_i(S_{\mu})$ muss jeweils das Minimum zwischen zwei Summen ermittelt werden:
- \[{\it \Gamma}_i(S_0) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_1)={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_2) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_3) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm}.\]
- Von den zwei an einem Knoten ${\it \Gamma}_i(S_{\mu})$ ankommenden Zweigen wird der schlechtere (der zu einem größeren ${\it \Gamma}_i(S_{\mu})$ geführt hätte) eliminiert. Zu jedem Knoten führt dann nur noch ein einziger Zweig.
- Sind alle Fehlergrößen bis einschließlich $i = 7$ ermittelt, so kann der Viterbi–Algotithmus mit der Suche des zusammenhängenden Pfades vom Ende des Trellis ⇒ ${\it \Gamma}_7(S_0)$ bis zum Anfang ⇒ ${\it \Gamma}_0(S_0)$ abgeschlossen werden.
- Durch diesen Pfad liegen dann die am wahrscheinlichsten erscheinende Codesequenz $\underline{z}$ und die wahrscheinlichste Informationssequenz $\underline{v}$ fest.
- Nicht für alle Empfangssequenzen $\underline{y}$ gilt aber $\underline{z} = \underline{x}$ und $\underline{v} = \underline{u}$. Das heißt: Bei zu vielen Übertragungsfehlern versagt auch der Viterbi–Algorithmus.
Erstellen des Trellis im fehlerfreien Fall – Fehlergrößenberechnung
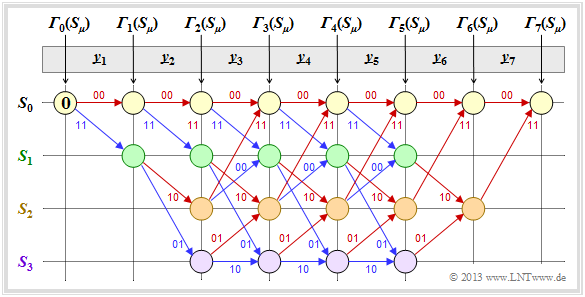
Zunächst gehen wir von der Empfangssequenz $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ aus, die hier – wegen der Codewortlänge $n = 2$ – bereits in Bitpaare $\underline{y}_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ \underline{y}_7$ unterteilt ist. Die in das Trellis eingetragenen Zahlenwerte und die verschiedenen Stricharten werden im folgenden Text erklärt.
- Ausgehend vom Initialwert ${\it \Gamma}_0(S_0) = 0$ kommt man mit $\underline{y}_1 = (11)$ durch Addition der Hamming-Distanzen
- $$d_{\rm H}((00), \ \underline{y}_1) = 2\text{ bzw. }d_{\rm H}((11), \ \underline{y}_1) = 0$$
- zu den Fehlergrößen ${\it \Gamma}_1(S_0) = 2, \ {\it \Gamma}_1(S_1) = 0$.
- Im zweiten Decodierschritt gibt es Fehlergrößen für alle vier Zustände: Mit $\underline{y}_2 = (01)$ erhält man:
- \[{\it \Gamma}_2(S_0) = {\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_1) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+2=2 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+0=0 \hspace{0.05cm}.\]
- In allen weiteren Decodierschritten müssen jeweils zwei Werte verglichen werden, wobei dem Knoten ${\it \Gamma}_i(S_{\mu})$ stets der kleinere Wert zugewiesen wird. Beispielsweise gilt für $i = 3$ mit $\underline{y}_3 = (01)$:
- \[{\it \Gamma}_3(S_0) ={\rm min} \left [{\it \Gamma}_{2}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \big ] = 3\hspace{0.05cm},\]
- \[{\it \Gamma}_3(S_3) ={\rm min} \left [{\it \Gamma}_{2}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+0\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.\]
- Ab $i = 6$ wird im betrachteten Beispiel die Terminierung des Faltungscodes wirksam. Hier sind nur noch zwei Vergleiche zur Bestimmung von ${\it \Gamma}_6(S_0) = 3$ und ${\it \Gamma}_6(S_2)= 0$ anzustellen, und für $i = 7$ nur noch ein einziger ein Vergleich mit dem Endergebnis ${\it \Gamma}_7(S_0) = 0$.
Die Beschreibung des Viterbi–Decodiervorgangs wird auf der nächsten Seite fortgesetzt.
Auswerten des Trellis im fehlerfreien Fall – Pfadsuche
Nachdem alle Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – im vorliegenden Beispiel für $1 ≤ i ≤ 7$ und $0 ≤ \mu ≤ 3$ – ermittelt wurden, kann der Viterbi–Decoder mit der Pfadsuche beginnen:
- Die Grafik zeigt das Trellis nach der Fehlergrößenberechnung. Alle Kreise sind mit Zahlenwerten belegt.
- Allerding ist der in der Grafik bereits eingezeichnete wahrscheinlichste Pfad noch nicht bekannt.
- Von den jeweils zwei an einem Knoten ankommenden Zweigen wird stets nur derjenige bei der abschließenden Pfadsuche herangezogen, der zur minimalen Fehlergröße ${\it \Gamma}_i(S_{\mu})$ geführt hat.
- Die „schlechten” Zweige werden verworfen. Sie sind in obiger Grafik jeweils punktiert dargestellt.
Die Pfadsuche läuft wie folgt ab:
- Ausgehend vom Endwert ${\it \Gamma}_7(S_0)$ wird in Rückwärtsrichtung ein zusammenhängender Pfad bis zum Startwert ${\it \Gamma}_0(S_0)$ gesucht. Erlaubt sind nur die durchgezogenen Zweige. Punktierte Linien können nicht Teil des ausgewählten Pfades sein.
- Der ausgewählte Pfad durchläuft von rechts nach links die Zustände $S_0 ← S_2 ← S_1 ← S_0 ← S_2 ← S_3 ← S_1 ← S_0$ und ist in der Grafik grau hinterlegt. Es gibt keinen zweiten durchgehenden Pfad von ${\it \Gamma}_7(S_0)$ zu ${\it \Gamma}_0(S_0)$. Das bedeutet: Das Decodierergebnis ist eindeutig.
- Das Ergebnis $\underline{v} = (1, 1, 0, 0, 1, 0, 0)$ des Viterbi–Decoders hinsichtlich der Informationssequenz erhält man, wenn man für den durchgehenden Pfad – nun aber in Vorwärtsrichtung von links nach rechts – die Farben der einzelnen Zweige auswertet $($rot entspricht einer $0$ und blau einer $1)$.
Aus dem Endwert ${\it \Gamma}_7(S_0) = 0$ erkennt man, dass in diesem ersten Beispiel keine Übertragungsfehler vorlagen:
- Das Decodierergebnis $\underline{z}$ stimmt also mit dem Empfangsvektor $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ und der tatsächlichen Codesequenz $\underline{x}$ überein.
- Bei fehlerfreier Übertragung ist $\underline{v}$ nicht nur die nach dem ML–Kriterium wahrscheinlichste Informationssequenz $\underline{u}$, sondern beide sind sogar identisch: $\underline{v} \equiv \underline{u}$.
Anmerkung: Bei der beschriebenen Decodierung wurde natürlich von der bereits in der Überschrift enthaltenen Information „Fehlerfreier Fall” kein Gebrauch gemacht.
Nun folgen drei Beispiele zur Viterbi–Decodierung für den fehlerbehafteten Fall.
Decodierbeispiele für den fehlerbehafteten Fall
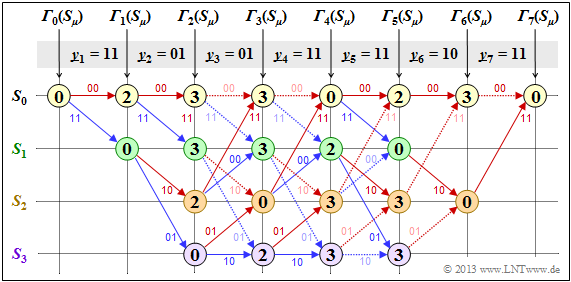
$\text{Beispiel 1:}$ Wir gehen hier vom Empfangsvektor $\underline{y} = \big (11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) $ aus, der keine gültige Codesequenz $\underline{x}$ darstellt. Die Berechnung der Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ und die Pfadsuche geschieht wie auf der Seite Vorbemerkungen beschrieben und auf den beiden letzten Seite für den fehlerfreien Fall demonstriert.
Als Resümee dieses ersten Beispiels ist festzuhalten:
- Auch beim obigen Trellis lässt sich ein eindeutiger Pfad (mit dunkelgrauer Hinterlegung) zurückverfolgen, der zu den folgenden Ergebnissen führt
(erkennbar an den Beschriftungen bzw. den Farben dieses Pfades):
- \[\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \big ) \hspace{0.05cm},\]
- \[ \underline{\upsilon} =\big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big ) \hspace{0.05cm}.\]
- Der Vergleich der am wahrscheinlichsten gesendeten Codesequenz $\underline{z}$ mit dem Empfangsvektor $\underline{y}$ zeigt, dass hier zwei Bitfehler (gleich am Beginn) vorlagen. Da aber der verwendete Faltungscode die freie Distanz $d_{\rm F} = 5$ aufweist, führen zwei Fehler noch nicht zu einem falschen Decodierergebnis.
- Es gibt andere Pfade wie zum Beispiel den heller markierten Pfad $(S_0 → S_1 → S_3 → S_3 → S_3 → S_2 → S_0 → S_0)$, die zunächst als vielversprechend erscheinen. Erst im letzten Decodierschritt $(i = 7)$ kann dieser hellgraue Pfad endgültig verworfen werden.
- Das Beispiel zeigt, dass eine zu frühe Entscheidung oft nicht zielführend ist. Man erkennt auch die Zweckmäßigkeit der Terminierung: Bei endgültiger Entscheidung bei $i = 5$ (Ende der Informationssequenz) wären die Sequenzen $(0, 1, 0, 1, 1)$ und $(1, 1, 1, 1, 0)$ noch als gleichwahrscheinlich angesehen worden.
Anmerkungen: Bei der Berechnung von ${\it \Gamma}_5(S_0) = 3$ und ${\it \Gamma}_5(S_1) = 3$ führen hier jeweils die beiden Vergleichszweige zur exakt gleichen minimalen Fehlergröße. In der Grafik sind diese beiden Sonderfälle durch Strichpunktierung markiert.
- In diesem Beispiel hat dieser Sonderfall keine Auswirkung auf die Pfadsuche.
- Der Algorithmus erwartet trotzdem stets eine Entscheidung zwischen zwei konkurrierenden Zweigen.
- In der Praxis hilft man sich dadurch, dass man bei Gleichheit einen der beiden Pfade zufällig auswählt.
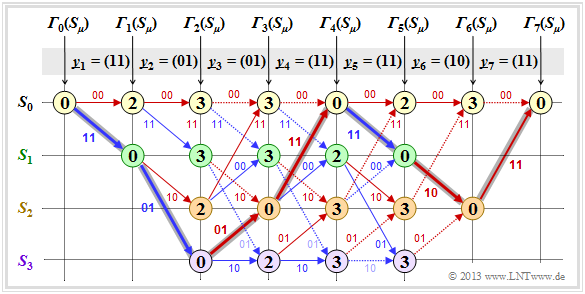
$\text{Beispiel 2:}$ Im diesem Beispiel gehen wir von folgenden Voraussetzungen bezüglich Quelle und Coder aus:
- \[\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.\]
Aus der Grafik erkennt man, dass sich hier der Decoder trotz dreier Bitfehler für den richtigen Pfad (dunkle Hinterlegung) entscheidet.
- Es gibt also nicht immer eine Fehlentscheidung, wenn mehr als $d_{\rm F}/2$ Bitfehler aufgetreten sind.
- Aber bei statistischer Verteilung der drei Übertragungsfehler würde häufiger falsch entschieden als richtig.
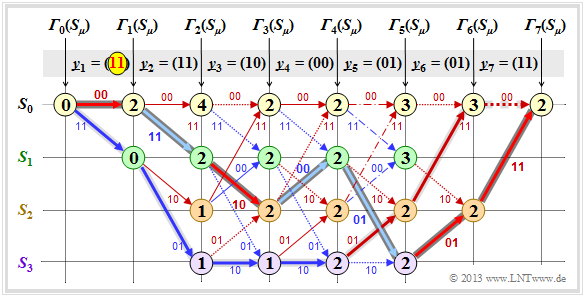
$\text{Beispiel 3:}$ Auch hier gelte \(\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.\) Im Unterschied zum $\text{Beispiel 2}$ ist aber noch ein vierter Bitfehler in Form von $\underline{y}_7 = (01)$ hinzugefügt.
- Nun führen beide Zweige im Schritt $i = 7$ zur minimalen Fehlergröße ${\it \Gamma}_7(S_0) = 4$, erkennbar an den strichpunktierten Übergängen. Entscheidet man sich im dann erforderlichen Losverfahren für den dunkel hinterlegten Pfad, so wird auch bei vier Bitfehlern noch die richtige Entscheidung getroffen: $\underline{v} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )$.
- Andernfalls kommt es zu einer Fehlentscheidung. Je nachdem, wie das Auswürfeln im Schritt $i =6$ zwischen den beiden strichpunktierten Konkurrenten ausgeht, entscheidet man sich entweder für den violetten oder den hellgrauen Pfad. Mit dem richtigen Pfad haben beide wenig gemein.
Zusammenhang zwischen Hamming–Distanz und Korrelation
Insbesondere beim BSC–Modell – aber auch bei jedem anderen Binärkanal ⇒ Eingang $x_i ∈ \{0,1\}$, Ausgang $y_i ∈ \{0,1\}$ wie zum Beispiel dem Gilbert–Elliott–Modell – liefert die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{y})$ genau die gleiche Information über die Ähnlichkeit der Eingangsfolge $\underline{x}$ und der Ausgangsfolge $\underline{y}$ wie das innere Produkt. Nimmt man an, dass die beiden Folgen in bipolarer Darstellung vorliegen (gekennzeichnet durch Tilden) und dass die Folgenlänge jeweils $L$ ist, so gilt für das innere Produkt:
- \[<\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} = \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.\]
Wir bezeichnen dieses innere Produkt manchmal auch als den "Korrelationswert". Im Unterschied zum Korrelationskoeffizienten kann der Korrelationswert den Wertebereich $±1$ durchaus überschreiten.
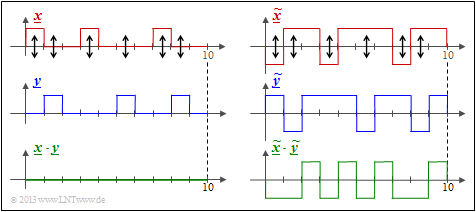
$\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.
- Links dargestellt sind die unipolaren Folgen $\underline{x}$ und $\underline{y}$ sowie das Produkt $\underline{x} \cdot \underline{y}$.
- Man erkennt die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{y}) = 6$ ⇒ sechs Bitfehler an den Pfeilpositionen.
- Das innere Produkt $ < \underline{x} \cdot \underline{y} > \hspace{0.15cm} = \hspace{0.15cm}0$ hat hier keine Aussagekraft. Zum Beispiel ist $< \underline{0} \cdot \underline{y} > $ unabhängig von $\underline{y}$ stets Null.
Die Hamming–Distanz $d_{\rm H} = 6$ erkennt man auch aus der bipolaren (antipodalen) Darstellung der rechten Grafik.
- Die „Korrelationswert” hat nun den richtigen Wert:
- $$4 \cdot (+1) + 6 \cdot (-1) = \, -2.$$
- Es gilt der deterministische Zusammenhang zwischen den beiden Größen mit der Folgenlänge $L$:
- $$ < \underline{ \tilde{x} } \cdot \underline{\tilde{y} } > \hspace{0.15cm} = \hspace{0.15cm} L - 2 \cdot d_{\rm H} (\underline{\tilde{x} }, \hspace{0.05cm}\underline{\tilde{y} })\hspace{0.05cm}. $$
$\text{Fazit:}$ Interpretieren wir nun diese Gleichung für einige Sonderfälle:
- Identische Folgen: Die Hamming–Distanz ist gleich $0$ und der „Korrelationswert” gleich $L$.
- Invertierte: Folgen: Die Hamming–Distanz ist gleich $L$ und der „Korrelationswert” gleich $-L$.
- Unkorrelierte Folgen: Die Hamming–Distanz ist gleich $L/2$, der „Korrelationswert” gleich $0$.
Viterbi–Algorithmus, basierend auf Korrelation und Metriken
Mit den Erkenntnissen der letzten Seite lässt sich der Viterbi–Algorithmus auch wie folgt charakterisieren.
$\text{Alternative Beschreibung:}$ Der Viterbi–Algorithmus sucht von allen möglichen Codesequenzen $\underline{x}' ∈ \mathcal{C}$ die Sequenz $\underline{z}$ mit dem maximalen „ Korrelationswert” zur Empfangssequenz $\underline{y}$:
- \[\underline{z} = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} \left\langle \tilde{\underline{x} }'\hspace{0.05cm} ,\hspace{0.05cm} \tilde{\underline{y} } \right\rangle \hspace{0.4cm}{\rm mit }\hspace{0.4cm}\tilde{\underline{x} }\hspace{0.05cm}'= 1 - 2 \cdot \underline{x}'\hspace{0.05cm}, \hspace{0.2cm} \tilde{\underline{y} }= 1 - 2 \cdot \underline{y} \hspace{0.05cm}.\]
$〈\ \text{ ...} \ 〉$ bezeichnet einen „Korrelationswert” entsprechend den Aussagen auf der letzten Seite. Die Tilden weisen wieder auf die bipolare (antipodale) Darstellung hin.
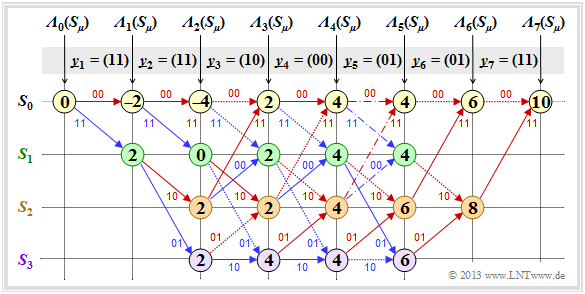
Die Grafik zeigt die diesbezügliche Trellisauswertung. Zugrunde liegt wie für die Trellisauswertung gemäß Beispiel 1 – basierend auf der minimalen Hamming–Distanz und den Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – wieder die Eingangsfolge $\underline{u} = \big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big )$ ⇒ Codefolge $\underline{x} = \big (00, 11, 10, 00, 01, 01, 11 \big ) \hspace{0.05cm}.$
Weiter werden vorausgesetzt:
- der Standard–Faltungscodierer: Rate $R = 1/2$, Gedächtnis $m = 2$;
- die Übertragungsfunktionsmatrix: $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$;
- Länge der Informationssequenz: $L = 5$;
- Berücksichtigung der Terminierung: $L' = 7$;
- der Empfangsvektor $\underline{y} = (11, 11, 10, 00, 01, 01, 11)$
⇒ zwei Bitfehler zu Beginn; - Viterbi–Decodierung mittels Trellisdiagramms:
- roter Pfeil ⇒ Hypothese $u_i = 0$,
- blauer Pfeil ⇒ Hypothese $u_i = 1$.
Nebenstehendes Trellis und die Trellisauswertung gemäß Beispiel 1 ähneln sich sehr. Ebenso wie die Suche nach der Sequenz mit der minimalen Hamming–Distanz geschieht auch die Suche nach dem maximalen Korrelationswert schrittweise:
- Die Knoten bezeichnet man hier als die Metriken ${\it \Lambda}_i(S_{\mu})$.
- Die englische Bezeichnung hierfür ist Cumulative Metric, während Branch Metric den Metrikzuwachs angibt.
- Der Endwert ${\it \Lambda}_7(S_0) = 10$ gibt den „Korrelationswert” zwischen der ausgewählten Folge $\underline{z}$ und dem Empfangsvektor $\underline{y}$ an.
- Im fehlerfreien Fall ergäbe sich ${\it \Lambda}_7(S_0) = 14$.
$\text{Beispiel 5:}$ Die folgende Detailbeschreibung der Trellisauswertung beziehen sich auf das obige Trellis:
- Die Metriken zum Zeitpunkt $i = 1$ ergeben sich mit $\underline{y}_1 = (11)$ zu
- \[{\it \Lambda}_1(S_0) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(+1,\hspace{0.05cm} +1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} -2 \hspace{0.05cm},\]
- \[{\it \Lambda}_1(S_1) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(-1,\hspace{0.05cm} -1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} +2 \hspace{0.05cm}.\]
- Entsprechend gilt zum Zeitpunkt $i = 2$ mit $\underline{y}_2 = (11)$:
- \[{\it \Lambda}_2(S_0) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2-2 = -4 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_1) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2+2 = 0 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_2)= {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_3)= {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm}.\]
- Ab dem Zeitpunkt $i =3$ muss eine Entscheidung zwischen zwei Metriken getroffen werden. Beispielsweise erhält man mit $\underline{y}_3 = (10)$ für die oberste und die unterste Metrik im Trellis:
- \[{\it \Lambda}_3(S_0)={\rm max} \left [{\it \Lambda}_{2}(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}> \right ] = {\rm max} \left [ -4+0\hspace{0.05cm},\hspace{0.05cm} +2+0 \right ] = +2\hspace{0.05cm},\]
- \[{\it \Lambda}_3(S_3) ={\rm max} \left [{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_3) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}> \right ] = {\rm max} \left [ 0+0\hspace{0.05cm},\hspace{0.05cm} +2+2 \right ] = +4\hspace{0.05cm}.\]
Vergleicht man die zu zu maximierenden Metriken ${\it \Lambda}_i(S_{\mu})$ mit den zu minimierenden Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ gemäß dem $\text{Beispiel 1}$, so erkennt man den folgenden deterministischen Zusammenhang:
- \[{\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [ i - {\it \Gamma}_i(S_{\mu}) \big ] \hspace{0.05cm}.\]
Die Auswahl der zu den einzelnen Decodierschritten überlebenden Zweige ist bei beiden Verfahren identisch, und auch die Pfadsuche liefert das gleiche Ergebnis.
$\text{Fazit:}$
- Beim Binärkanal – zum Beispiel nach dem BSC–Modell – führen die beiden beschriebenen Viterbi–Varianten „Fehlergrößenminimierung” und „Metrikmaximierung” zum gleichen Ergebnis.
- Beim AWGN–Kanal ist dagegen die Fehlergrößenminimierung nicht anwendbar, da keine Hamming–Distanz zwischen dem binären Eingang $\underline{x}$ und dem analogen Ausgang $\underline{y}$ angegeben werden kann.
- Die Metrikmaximierung ist beim AWGN–Kanal vielmehr identisch mit der Minimierung der Euklidischen Distanz – siehe Aufgabe 3.10Z.
- Ein weiterer Vorteil der Metrikmaximierung ist, dass eine Zuverlässigkeitsinformation über die Empfangswerte $\underline{y}$ in einfacher Weise berücksichtigt werden kann.
Viterbi–Entscheidung bei nicht–terminierten Faltungscodes
Bisher wurde stets ein terminierter Faltungscode der Länge $L\hspace{0.05cm}' = L + m$ betrachtet, und das Ergebnis des Viterbi–Decoders war der durchgehende Trellispfad vom Startzeitpunkt $(i = 0)$ bis zum Ende $(i = L\hspace{0.05cm}')$.
- Bei nicht–terminierten Faltungscodes $(L\hspace{0.05cm}' → ∞)$ ist diese Entscheidungsstrategie nicht anwendbar.
- Hier muss der Algorithmus abgewandelt werden, um in endlicher Zeit eine bestmögliche Schätzung (gemäß Maximum–Likelihood) der einlaufenden Bits der Codesequenz liefern zu können.
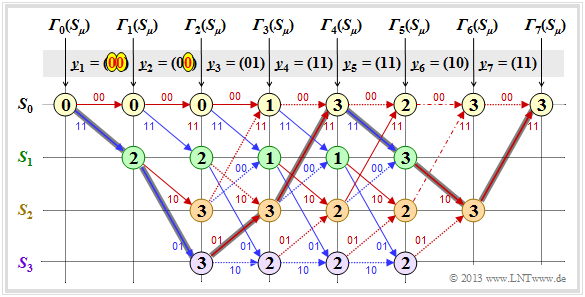
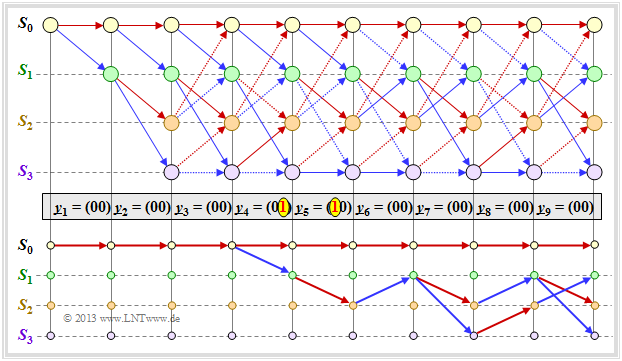
Die Grafik zeigt im oberen Teil ein beispielhaftes Trellis für
- „unseren” Standard–Codierer ⇒ $R = 1/2, \ m = 2, \ {\rm G}(D) = (1 + D + D^2, \ 1 + D^2)$,
- die Nullfolge ⇒ $\underline{u} = \underline{0} = (0, 0, 0, \ \text{...})$ ⇒ $\underline{x} = \underline{0} = (00, 00, 00, \ \text{...})$,
- jeweils einen Übertragungsfehler bei $i = 4$ und $i = 5$.
Anhand der Stricharten erkennt man erlaubte (durchgezogene) und verbotene (punktierte) Pfeile in rot $(u_i = 0)$ und blau $(u_i = 1)$. Punktierte Linien haben einen Vergleich gegen einen Konkurrenten verloren und können nicht Teil des ausgewählten Pfades sein.
Der untere Teil der Grafik zeigt die $2^m = 4$ überlebenden Pfade ${\it \Phi}_9(S_{\mu})$ zum Zeitpunkt $i = 9$.
- Man findet diese Pfade am einfachsten von rechts nach links (Rückwärtsrichtung).
- Die folgende Angabe zeigt die durchlaufenen Zustände $S_{\mu}$ allerdings in Vorwärtsrichtung:
- $${\it \Phi}_9(S_0) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0,$$
- $${\it \Phi}_9(S_1) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_3 → S_2 → S_1,$$
- $${\it \Phi}_9(S_2) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_2,$$
- $${\it \Phi}_9(S_3) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_3.$$
Zu früheren Zeitpunkten $(i<9)$ würden sich andere überlebende Pfade ${\it \Phi}_i(S_{\mu})$ ergeben. Deshalb definieren wir:
$\text{Definition:}$ Der überlebende Pfad (englisch: Survivor) ${\it \Phi}_i(S_{\mu})$ ist der durchgehende Pfad vom Start $S_0$ $($bei $i = 0)$ zum Knoten $S_{\mu}$ zum Zeitpunkt $i$. Empfehlenswert ist die Pfadsuche in Rückwärtsrichtung.
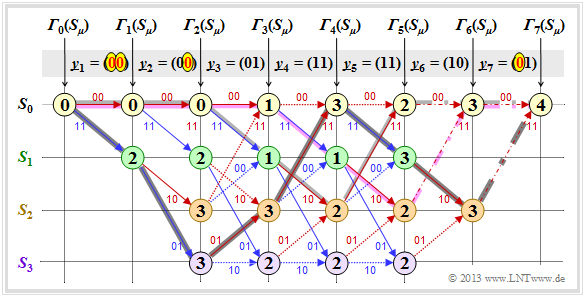
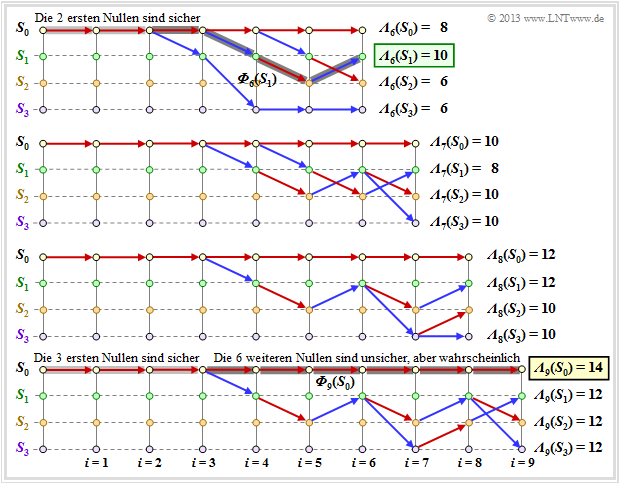
Die folgende Grafik zeigt die überlebenden Pfade für die Zeitpunkte $i = 6$ bis $i = 9$. Zusätzlich sind die jeweiligen Metriken ${\it \Lambda}_i(S_{\mu})$ für alle vier Zustände angegeben.
Diese Grafik ist wie folgt zu interpretieren:
- Zum Zeitpunkt $i = 9$ kann noch keine endgültige ML–Entscheidung über die ersten neun Bit der Informationssequenz getroffen werden. Allerdings ist bereits sicher, dass die wahrscheinlichste Bitfolge durch einen der Pfade ${\it \Phi}_9(S_0), \ \text{...} \ , \ {\it \Phi}_9(S_3)$ richtig wiedergegeben wird.
- Da alle vier Pfade bis $i = 3$ identisch sind, ist die Entscheidung „$v_1 = 0, v_2 = 0, \ v_3 = 0$” die bestmögliche (hellgraue Hinterlegung). Auch zu einem späteren Zeitpunkt würde keine andere Entscheidung getroffen werden. Hinsichtlich der Bits $v_4, \ v_5, \ \text{...}$ sollte man sich zu diesem frühen Zeitpunkt noch nicht festlegen.
- Müsste man zum Zeitpunkt $i = 9$ eine Zwangsentscheidung treffen, so würde man sich für ${\it \Phi}_9(S_0)$ ⇒ $\underline{v} = (0, 0, \ \text{...} \ , 0)$ entscheiden, da die Metrik ${\it \Lambda}_9(S_0) = 14$ größer ist als die Vergleichsmetriken.
- Die Zwangsentscheidung zum Zeitpunkt $i = 9$ führt in diesem Beispiel zum richtigen Ergebnis. Zum Zeitpunkt $i = 6$ wäre ein solcher Zwangsentscheid falsch gewesen ⇒ $\underline{v} = (0, 0, 0, 1, 0, 1)$, und zu den Zeitpunten $i = 7$ bzw. $i = 8$ nicht eindeutig.
Weitere Decodierverfahren für Faltungscodes
Wir haben uns bisher nur mit dem Viterbi–Algorithmus in der Form beschäftigt, der 1967 von Andrew J. Viterbi in [Vit67][1] veröffentlicht wurde. Erst 1974 hat George David Forney nachgewiesen, dass dieser Algorithmus eine Maximum–Likelihood–Decodierung von Faltungscodes durchführt.
Aber schon in den Jahren zuvor waren viele Wissenschaftler sehr bemüht, effiziente Decodierverfahren für die 1955 erstmals von Peter Elias beschriebenen Faltungscodes bereitzustellen. Zu nennen sind hier unter Anderem – genauere Beschreibungen findet man beispielsweise in [Bos98][2] oder der englischen Ausgabe [Bos99][3].
- Sequential Decoding von J. M. Wozencraft und B. Reiffen aus dem Jahre 1961,
- der Vorschlag von Robert Mario Fano (1963), der als Fano–Algorithmus bekannt wurde,
- die Arbeiten von Kamil Zigangirov (1966) und Frederick Jelinek (1969), deren Decodierverfahren auch als Stack–Algorithmus bezeichnet wird.
Alle diese Decodierverfahren und auch der Viterbi–Algorithmus in seiner bisher beschriebenen Form liefern „hart” entschiedene Ausgangswerte ⇒ $v_i ∈ \{0, 1\}$. Oftmals wären jedoch Informationen über die Zuverlässigkeit der getroffenen Entscheidungen wünschenswert, insbesondere dann, wenn ein verkettetes Codierschema mit einem äußeren und einem inneren Code vorliegt.
Kennt man die Zuverlässigkeit der vom inneren Decoder entschiedenen Bits zumindest grob, so kann durch diese Information die Bitfehlerwahrscheinlichkeit des äußeren Decoders (signifikant) herabgesetzt werden. Der von Joachim Hagenauer in [Hag90][4] vorgeschlagene Soft–Output–Viterbi–Algorithmus (SOVA) erlaubt es, zusätzlich zu den entschiedenen Symbolen auch jeweils ein Zuverlässigkeitsmaß anzugeben.
Abschließend gehen wir noch etwas genauer auf den BCJR–Algorithmus ein, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv [BCJR74][5].
- Während der Viterbi–Algorithmus nur eine Schätzung der Gesamtsequenz vornimmt ⇒ block–wise ML, schätzt der BCJR–Algorithmus ein einzelnes Symbol (Bit) unter Berücksichtigung der gesamten empfangenen Codesequenz.
- Es handelt sich hierbei also um eine symbolweise Maximum–Aposteriori–Decodierung ⇒ bit–wise MAP.
$\text{Fazit:}$ Der Unterschied zwischen Viterbi–Algorithmus und BCJR–Algorithmus soll – stark vereinfacht – am Beispiel eines terminierten Faltungscodes dargestellt werden:
- Der Viterbi–Algorithmus arbeitet das Trellis nur in einer Richtung – der Vorwärtsrichtung – ab und berechnet für jeden Knoten die Metriken ${\it \Lambda}_i(S_{\mu})$. Nach Erreichen des Endknotens wird der überlebende Pfad gesucht, der die wahrscheinlichste Codesequenz kennzeichnet.
- Beim BCJR–Algorithmus wird das Trellis zweimal abgearbeitet, einmal in Vorwärtsrichtung und anschließend in Rückwärtsrichtung. Für jeden Knoten sind dann zwei Metriken angebbar, aus denen für jedes Bit die Aposterori–Wahrscheinlichkeit bestimmt werden kann.
Hinweise:
- Diese Kurzzusammenfassung basiert auf dem Lehrbüchern [Bos98][2] bzw. [Bos99][3].
- Eine etwas ausführlichere Beschreibung des BCJR–Algorithmus' folgt auf der Seite Hard Decision vs. Soft Decision im vierten Hauptkapitel „Iterative Decodierverfahren”.
Aufgaben zum Kapitel
Aufgabe 3.9: Grundlegendes zum Viterbi–Algorithmus
Aufgabe 3.9Z: Nochmals Viterbi–Algorithmus
Aufgabe 3.10: Fehlergrößenberechnung
Aufgabe 3.10Z: ML–Decodierung von Faltungscodes
Aufgabe 3.11: Viterbi–Pfadsuche
Quellenverzeichnis
- ↑ Viterbi, A.J.: Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm. In: IEEE Transactions on Information Theory, vol. IT-13, pp. 260-269, April 1967.
- ↑ 2,0 2,1 Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998.
- ↑ 3,0 3,1 Bossert, M.: Channel Coding for Telecommunications. Wiley & Sons, 1999.
- ↑ Hagenauer, J.: Soft Output Viterbi Decoder. In: Technischer Report, Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), 1990.
- ↑ Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate. In: IEEE Transactions on Information Theory, Vol. IT-20, S. 284-287, 1974.