Applets:Impulse und Spektren: Unterschied zwischen den Versionen
Tasnad (Diskussion | Beiträge) |
|||
| Zeile 1: | Zeile 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|impulsesAndSpectra}} |
[https://en.lntwww.de/Applets:Impulses_and_Spectra '''English Version'''] | [https://en.lntwww.de/Applets:Impulses_and_Spectra '''English Version'''] | ||
| Zeile 236: | Zeile 236: | ||
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|impulsesAndSpectra}} |
[https://en.lntwww.de/Applets:Impulses_and_Spectra '''English Version'''] | [https://en.lntwww.de/Applets:Impulses_and_Spectra '''English Version'''] | ||
<br><br> | <br><br> | ||
Version vom 18. August 2020, 13:59 Uhr
Applet in neuem Tab öffnen English Version
Inhaltsverzeichnis
- 1 Programmbeschreibung
- 2 Theoretischer Hintergrund
- 2.1 Zusammenhang $x(t)\Leftrightarrow X(f)$
- 2.2 Gaußimpuls $\Rightarrow$ Gaussian Pulse
- 2.3 Rechteckimpuls $\Rightarrow$ Rectangular Pulse
- 2.4 Dreieckimpuls $\Rightarrow$ Dreieckimpuls Triangular Pulse
- 2.5 Trapezimpuls $\Rightarrow$ Trapezoidal Pulse
- 2.6 Cosinus-Rolloff-Impuls $\Rightarrow$ Cosine-rolloff Pulse
- 2.7 Cosinus-Quadrat-Impuls
- 3 Versuchsdurchführung
- 4 Zur Handhabung des Programms
- 5 Über die Autoren
- 6 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Programmbeschreibung
Dargestellt werden impulsförmige symmetrische Zeitsignale ⇒ „Impulse” $x(t)$ und die dazugehörigen Spektralfunktionen $X(f)$, nämlich
- Gaußimpuls (englisch: Gaussian pulse),
- Rechteckimpuls (englisch: Rectangular pulse),
- Dreieckimpuls (englisch: Triangular pulse),
- Trapezimpuls (englisch: Trapezoidal pulse),
- Cosinus–Rolloff–Impuls (englisch: Cosine-rolloff pulse).
Weiter ist zu beachten:
- Die Funktionen $x(t)$ bzw. $X(f)$ werden für bis zu zwei Parametersätzen in jeweils einem Diagramm dargestellt.
- Die roten Kurven und Zahlenangaben gelten für den linken Parametersatz, die blauen für den rechten Parametersatz.
- Die Abszissen $t$ (Zeit) und $f$ (Frequenz) sowie die Ordinaten $x(t)$ (Signalwerte) bzw. $X(f)$ (Spektralwerte) sind jeweils normiert.
Theoretischer Hintergrund
Zusammenhang $x(t)\Leftrightarrow X(f)$
- Der Zusammenhang zwischen der Zeitfunktion $x(t)$ und dem Spektrum $X(f)$ ist durch das erste Fourierintegral gegeben:
- $$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$
- Um aus der Spektralfunktion $X(f)$ die Zeitfunktion $x(t)$ berechnen zu können, benötigt man das zweite Fourierintegral:
- $$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$
- In allen Beispielen verwenden wir reelle und gerade Funktionen. Somit gilt:
- $$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$
- $x(t)$ und $X(f)$ haben unterschiedliche Einheiten, beispielsweise $x(t)$ in $\rm V$, $X(f)$ in $\rm V/Hz$.
- Der Zusammenhang zwischen diesem Modul und dem ähnlich aufgebauten Applet Frequenzgang & Impulsantwort basiert auf dem Vertauschungssatz.
- Alle Zeiten sind auf eine Zeit $T$ normiert und alle Frequenzen auf $1/T$ ⇒ die Spektralwerte $X(f)$ müssen noch mit der Normierungszeit $T$ multipliziert werden.
$\text{Beispiel:}$ Stellt man einen Rechteckimpuls mit Amplitude $A_1 = 1$ und äquivalenter Impulsdauer $\Delta t_1 = 1$ ein, so ist $x_1(t)$ im Bereich $-0.5 < t < +0.5$ gleich Eins und außerhalb dieses Bereichs gleich Null. Die Spektralfunktion $X_1(f)$ verläuft $\rm si$–förmig mit $X_1(f= 0) = 1$ und der ersten Nullstelle bei $f=1$.
- Soll mit dieser Einstellung ein Rechteckimpuls mit $A = K = 3 \ \rm V$ und $\Delta t = T = 2 \ \rm ms$ nachgebildet werden, dann sind alle Signalwerte mit $K = 3 \ \rm V$ und alle Spektralwerte mit $K \cdot T = 0.006 \ \rm V/Hz$ zu multiplizieren.
- Der maximale Spektralwert ist dann $X(f= 0) = 0.006 \ \rm V/Hz$ und die erste Nullstelle liegt bei $f=1/T = 0.5 \ \rm kHz$.
Gaußimpuls $\Rightarrow$ Gaussian Pulse
- Die Zeitfunktion des Gaußimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
- $$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$
- Die äquivalente Zeitdauer $\Delta t$ ergibt sich aus dem flächengleichen Rechteck.
- Der Wert bei $t = \Delta t/2$ ist um den Faktor $0.456$ kleiner als der Wert bei $t=0$.
- Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
- $$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$
- Je kleiner die äquivalente Zeitdauer $\Delta t$ ist, um so breiter und niedriger ist das Spektrum ⇒ Reziprozitätsgesetz von Bandbreite und Impulsdauer.
- Sowohl $x(t)$ als auch $X(f)$ sind zu keinem $f$– bzw. $t$–Wert exakt gleich Null.
- Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden. Zum Beispiel ist $x(t)$ bereits bei $t=1.5 \Delta t$ auf weniger als $0.1\% $ des Maximums abgefallen.
Rechteckimpuls $\Rightarrow$ Rectangular Pulse
- Die Zeitfunktion des Rechteckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
- Der $\pm \Delta t/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
- Für die Spektralfunktion erhält man entsprechend den Gesetzmäßigkeiten der Fouriertransformation (1. Fourierintegral):
- $$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{mit} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$
- Der Spektralwert bei $f=0$ ist gleich der Rechteckfläche der Zeitfunktion.
- Die Spektralfunktion besitzt Nullstellen in äquidistanten Abständen $1/\Delta t$.
- Das Integral über der Spektralfunktion $X(f)$ ist gleich dem Signalwert zum Zeitpunkt $t=0$, also der Impulshöhe $K$.
Dreieckimpuls $\Rightarrow$ Dreieckimpuls Triangular Pulse
- Die Zeitfunktion des Dreieckimpulses mit der Höhe $K$ und der (äquivalenten) Dauer $\Delta t$ lautet:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
- Die absolute Zeitdauer ist $2 \cdot \Delta t$; diese ist doppelt so groß als die des Rechtecks.
- Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
- $$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
- Obige Zeitfunktion ist gleich der Faltung zweier Rechteckimpulse, jeweils mit Breite $\Delta t$.
- Daraus folgt: $X(f)$ beinhaltet anstelle der ${\rm si}$-Funktion die ${\rm si}^2$-Funktion.
- $X(f)$ weist somit ebenfalls Nullstellen im äquidistanten Abständen $1/\Delta f$ auf.
- Der asymptotische Abfall von $X(f)$ erfolgt hier mit $1/f^2$, während zum Vergleich der Rechteckimpuls mit $1/f$ abfällt.
Trapezimpuls $\Rightarrow$ Trapezoidal Pulse
Die Zeitfunktion des Trapezimpulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
- Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
- Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:
- $$r=\frac{t_2-t_1}{t_2+t_1}.$$
- Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Dreieckimpuls.
- Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
- $$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
- Der asymptotische Abfall von $X(f)$ liegt zwischen $1/f$ $($für Rechteck, $r=0)$ und $1/f^2$ $($für Dreieck, $r=1)$.
Cosinus-Rolloff-Impuls $\Rightarrow$ Cosine-rolloff Pulse
Die Zeitfunktion des Cosinus-Rolloff-Impulses mit der Höhe $K$ und den Zeitparametern $t_1$ und $t_2$ lautet:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
- Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt: $\Delta t = t_1+t_2$.
- Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:
- $$r=\frac{t_2-t_1}{t_2+t_1}.$$
- Der Sonderfall $r=0$ entspricht dem Rechteckimpuls und der Sonderfall $r=1$ dem Cosinus-Quadrat-Impuls.
- Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
- $$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
- Je größer der Rolloff-Faktor $r$ ist, desto schneller nimmt $X(f)$ asymptotisch mit $f$ ab.
Cosinus-Quadrat-Impuls
- Dies ist ein Sonderfall des Cosinus-Rolloff-Impulses und ergibt sich für $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
- Für die Spektralfunktion erhält man gemäß der Fouriertransformation:
- $$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
- Wegen der letzten ${\rm si}$-Funktion ist $X(f)=0$ für alle Vielfachen von $F=1/\Delta t$. Die äquidistanten Nulldurchgänge des Cos-Rolloff-Impulses bleiben erhalten.
- Aufgrund des Klammerausdrucks weist $X(f)$ nun weitere Nulldurchgänge bei $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... auf.
- Für die Frequenz $f=\pm F/2$ erhält man die Spektralwerte $K\cdot \Delta t/2$.
- Der asymptotische Abfall von $X(f)$ verläuft in diesem Sonderfall mit $1/f^3$.
Versuchsdurchführung
- Wählen Sie zunächst die Nummer $(1,\ 2$, ... $)$ der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer $0$ entspricht einem „Reset”: Einstellung wie beim Programmstart.
- „Rot” bezieht sich auf den ersten Parametersatz ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$.
- „Blau” bezieht sich auf den zweiten Parametersatz ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
- Werte betragsmäßig kleiner $0.0005$ werden im Programm zu Null gesetzt.
(1) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1, \Delta t_2 = 1)$ ⇒ Voreinstellung.
Welche Unterschiede erkennt man im Zeit- und im Frequenzbereich?
- Der Gaußimpuls reicht sowohl im Zeit– als auch im Frequenzbereich theoretisch bis ins Unendliche.
- Praktisch sind aber $x_1(t)$ für $|t| > 1.5$ und $X_1(f)$ für $|f| > 1.5$ nahezu Null.
- Das Rechteck ist zeitlich steng begrenzt: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ hat in einem viel größeren Bereich als $X_1(f)$ Anteile.
- Es gilt $X_1(f = 0) = X_2(f = 0)$, weil das Integral über den Gaußimpuls $x_1(t)$ gleich dem Integral über den Rechteckimpuls $x_2(t)$ ist.
(2) Vergleichen Sie den roten Gaußimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1,\Delta t_2)$.
Variieren Sie die äquivalente Impulsdauer $\Delta t_2$ zwischen $0.5$ und $2$. Interpretieren Sie die dargestellten Graphen.
- Man erkennt das Reziprozitätsgesetz von Bandbreite und Impulsdauer. Je größer $\Delta t_2$ ist, um so höher und schmäler ist die Spektralfunktion $X_2(f)$.
- Bei jeder Einstellung von $\Delta t_2$ sind die Zeitsignalwerte $x_1(t= 0)$ und $x_2(t=0)$ gleich ⇒ Auch die Integrale über $X_1(f)$ und $X_2(f)$ sind identisch.
(3) Vergleichen Sie den roten Rechteckimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem blauen Rechteckimpuls $(A_2 = 1,\Delta t_2 = 0.5)$.
Variieren Sie $\Delta t_2$ zwischen $0.05$ und $2$. Interpretieren Sie die dargestellten Graphen und extrapolieren Sie das Ergebnis.
- Das blaue Spektrum ist nun doppelt so breit wie das rote, aber nur halb so hoch. Erste Nullstelle von $X_1(f)$ bei $f =1$ und von $X_2(f)$ erst bei $f =2$.
- Verkleinerung von $\Delta t_2$: $X_2(f)$ immer niedriger und breiter. Sehr flacher Verlauf bei $\Delta t_2 = 0.05$: $X_2(f = 0)= 0.05$, $X_2(f = \pm 3)= 0.048$.
- Würde man $\Delta t_2 = \varepsilon \to 0$ wählen (im Programm nicht möglich), so ergäbe sich das nahezu konstante, sehr kleine Spektrum $X_2(f)=A \cdot \varepsilon \to 0$.
- Erhöht man die Amplitude auf $A=1/\varepsilon$, so ergibt sich die konstante Spektralfunktion $X_2(f) = 1$ der Diracfunktion $\delta(t)$. Das bedeutet:
- $\delta(t)$ ist durch ein Rechteck mit Breite $\Delta t = \varepsilon \to 0$ und Höhe $A = 1/\varepsilon \to \infty$ approximierbar. Das Diracgewicht ist Eins: $x(t) = 1 \cdot \delta (t)$.
(4) Vergleichen Sie den Rechteckimpuls $(A_1 = 1, \Delta t_1 = 1)$ mit dem Dreieckimpuls $(A_2 = 1,\Delta t_2 = 1)$. Interpretieren Sie die Spektalfunktionen.
- Das (normierte) Spektrum des Rechtecks $x_1(t)$ mit den (normierte) Parametern $A_1 = 1, \ \Delta t_1 = 1$ lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
- Die Faltung des Rechtecks $x_1(t)$ mit sich selbst ergibt das Dreieck $x_2(t) = x_1(t) \star x_1(t)$. Nach dem Faltungssatz gilt somit $X_2(f) = \big [X_1(f)\big]^2 $.
- Durch das Quadrieren der $\rm si$–förmigen Spektralfunktion $X_1(f)$ bleiben die Nullstellen in $X_2(f)$ erhalten. Es gilt aber nun $X_2(f) \ge 0$.
(5) Vergleichen Sie den Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem Dreieckimpuls $(A_2 = 1,\Delta t_2 = 1)$.
Variieren Sie $r_1$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_1(f)$.
- Der Trapezimpuls mit Rolloff-Faktor $r_1= 0$ ist identisch mit dem Rechteckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}(\pi\cdot f)$.
- Der Trapezimpuls mit Rolloff-Faktor $r_1= 1$ ist identisch mit dem Dreieckimpuls. Das „normierte Spektrum” lautet: $X_1(f)= {\rm si}^2(\pi\cdot f)$.
- In beiden Fällen besitzt $X_1(f)$ äquidistante Nulldurchgänge bei $\pm 1$, $\pm 2$, ... (sonst keine). Mit $0 < r_1 < 1$ gibt es abhängig von $r_1$ weitere Nulldurchgänge.
(6) Vergleichen Sie den Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ mit dem Cosinus-Rolloff-Impuls $(A_2 = 1,\Delta t_2 = 1.0, r_1 = 0.5)$.
Variieren Sie $r_2$ zwischen $0$ und $1$. Interpretieren Sie die Spektalfunktion $X_2(f)$ für $r_2 = 0.7$.
- Bei gleichem $r= 0.5$ besitzt der Cosinus-Rolloff-Impuls $X_2(f)$ ⇒ für $f > 1$ betragsmäßig größere Anteile als der Trapezimpuls.
- Bei gleichem Rolloff-Faktor $(r_1 = r_2= 0.5)$ verläuft der Abfall von $X_2(f)$ um die Frequenz $f = 0.5$ steiler als der Abfall von $X_1(f)$.
- Mit $r_1 = 0.5$ und $r_2 = 0.7$ gilt $x_1(t) \approx x_2(t)$ und damit auch $X_1(f) \approx X_2(f)$. Vergleichbare Flankensteilheit.
(7) Vergleichen Sie den roten Trapezimpuls $(A_1 = 1, \Delta t_1 = 1, r_1 = 1)$ mit dem blauen Cosinus-Rolloff-Impuls $(A_2 = 1,\Delta t_2 = 1.0, r_2 = 1)$.
Interpretieren Sie die Zeitfunktion $x_2(t)$ und die Spektralfunktion $X_2(f)$ systemtheoretisch.
- Es handelt sich bei $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \text{für} \ |t| \le 1$ um den Cosinus-Quadrat-Impuls. Nulldurchgänge bei $f = \pm 1$, $\pm 2$, ...
- Für die Frequenz $f=\pm 0.5$ erhält man die Spektralwerte $X_2(f)=0.5$. Der asymptotische Abfall verläuft hier mit $1/f^3$.
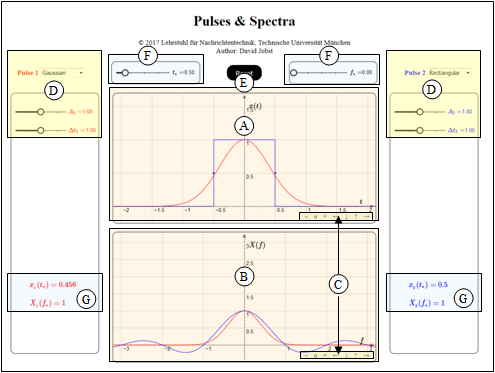
Zur Handhabung des Programms
(A) Bereich der graphischen Darstellung für $x(t)$
(B) Bereich der graphischen Darstellung für $X(f)$
(C) Variationsmöglichkeit für die graphischen Darstellungen
(D) Parametereingabe per Slider
links (rot): „Pulse 1”, rechts (blau): „Pulse 2”
(E) Parameter entsprechend der Voreinstellung ⇒ „Reset”
(F) Einstellung von $t_*$ und $f_*$ für Numerikausgabe
(G) Numerikausgabe von $x(t_*)$ und $X(f_*)$
links (rot): „Pulse 1”, rechts (blau): „Pulse 2”
Details zum obigen Punkt (C)
(*) Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
(*) Verschiebe–Funktionen „$\leftarrow$” (Bildausschnitt nach links, Ordinate nach rechts) sowie „$\uparrow$” „$\downarrow$” „$\rightarrow$”
Andere Möglichkeiten:
- Bei gedrückter Shifttaste und Scrollen kann im Koordinatensystem gezoomt werden.
- Bei gedrückter Shifttaste und gedrückter linker Maustaste kann das Koordinatensystem verschoben werden.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder und Klaus Eichin).
- 2017 wurde „Impulse & Spektren” von David Jobst im Rahmen seiner Ingenieurspraxis (Betreuer: Tasnád Kernetzky) auf „HTML5” umgesetzt und neu gestaltet.
- Letztmalige Überarbeitung 2020 durch Carolin Mirschina im Rahmen einer Werkstudententätigkeit.