Applets:Zur Verdeutlichung des Dopplereffekts: Unterschied zwischen den Versionen
| Zeile 342: | Zeile 342: | ||
:* Wie in der Aufgabe '''(6)''' sind auch hier nur Werte zwischen $f_{\rm D}=0.4$ und $f_{\rm D}=-0.4$ möglich, aber nun alle Zwischenwerte im Bereich $-0.4 \le f_{\rm D} \le +0.4$. | :* Wie in der Aufgabe '''(6)''' sind auch hier nur Werte zwischen $f_{\rm D}=0.4$ und $f_{\rm D}=-0.4$ möglich, aber nun alle Zwischenwerte im Bereich $-0.4 \le f_{\rm D} \le +0.4$. | ||
:* Wie Sie mit dem Button „Step” zeigen können, kommt der Dopplerwert $f_{\rm D}=0$ nur vor, wenn der Empfänger genau unterhalb des Senders liegt $(\alpha=\pm 90^\circ)$. | :* Wie Sie mit dem Button „Step” zeigen können, kommt der Dopplerwert $f_{\rm D}=0$ nur vor, wenn der Empfänger genau unterhalb des Senders liegt $(\alpha=\pm 90^\circ)$. | ||
| − | :* Dagegen sind Dopplerfrequenzen an den beiden Rändern $(|f_{\rm D}| = 0.4 -\varepsilon$, wobei $\varepsilon$ eine kleine positive Größe angibt$)$, sehr viel häufiger. | + | :* Dagegen sind Dopplerfrequenzen an den beiden Rändern $(|f_{\rm D}| = 0.4 -\varepsilon$, wobei $\varepsilon$ eine kleine positive Größe angibt$)$, sehr viel häufiger. |
| + | :* Schon aus diesem Versuch wird der prinzipielle Verlauf von Doppler–WDF und Doppler–LDS ⇒ „Jakes–Spektrum” erklärbar. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(8)''' Was ändert sich, wenn der Sender bei sonst gleichen Einstellungen fest am oberen Rand der Grafikfläche in der Mitte liegt $(300,\ 400) $? }} | ||
| + | :* Die Dopplerwerte $f_{\rm D} \approx0$ werden häufiger, solche an den Rändern seltener. Aufgrund der begrenzten Zeichenfläche gibt es keine Werte $|f_{\rm D}| > 0.325$. | ||
Version vom 8. Juni 2020, 10:47 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Das Applet behandelt die Systemkomponenten „Abtastung” und „Signalrekonstruktion”, zwei Komponenten, die zum Beispiel für das Verständnis der Pulscodemodulation $({\rm PCM})$ von großer Wichtigkeit sind. Die obere Grafik zeigt das für dieses Applet zugrundeliegende Modell. Darunter gezeichnet sind die Abtastwerte $x(\nu \cdot T_{\rm A})$ des zeitkontinuierlichen Signals $x(t)$. Die (unendliche) Summe über alle diese Abtastwerte bezeichnen wir als das abgetastete Signal $x_{\rm A}(t)$.
- Beim Sender wird aus dem zeitkontinuierlichen Quellensignal $x(t)$ das zeitdiskrete (abgetastete) Signal $x_{\rm A}(t)$ gewonnen. Man nennt diesen Vorgang Abtastung oder A/D–Wandlung.
- Der entsprechende Programmparameter für den Sender ist die Abtastrate $f_{\rm A}= 1/T_{\rm A}$. In der unteren Grafik ist der Abtastabstand $T_{\rm A}$ eingezeichnet.
- Beim Empfänger wird aus dem zeitdiskreten Empfangssignal $y_{\rm A}(t)$ das zeitkontinuierliche Sinkensignal $y(t)$ erzeugt ⇒ Signalrekonstruktion oder D/A–Wandlung entsprechend dem Empfänger–Frequenzgang $H_{\rm E}(f)$.
Das Applet berücksichtigt nicht die PCM–Blöcke „Quantisierung”, „Codierung / Decodierung” und der Digitale Übertragungskanal ist als ideal angenommen.
Theoretischer Hintergrund
Phänomenologische Beschreibung des Dopplereffekts
$\text{Definition:}$ Als $\rm Dopplereffekt$ bezeichnet man die Veränderung der wahrgenommenen Frequenz von Wellen jeder Art, die sich dann ergibt, wenn sich Quelle (Sender) und Beobachter (Empfänger) relativ zueinander bewegen. Dieser wurde Mitte des 19. Jahrhunderts von dem österreichischen Mathematiker, Physiker und Astronomen Christian Andreas Doppler theoretisch vorhergesagt und nach ihm benannt.
Qualitativ lässt sich der Dopplerreffekt wie folgt beschreiben:
- Nähern sich Beobachter und Quelle einander an, so erhöht sich aus Sicht des Beobachters die Frequenz, egal, ob sich der Beobachter bewegt oder die Quelle oder beide.
- Entfernt sich die Quelle vom Beobachter oder der Beobachter von der Quelle, so nimmt der Beobachter eine niedrigere Frequenz wahr, als tatsächlich gesendet wurde.
$\text{Beispiel 1:}$ Wir betrachten die Tonhöhenänderung des „Martinhorns” eines Rettungswagens. Solange sich das Fahrzeug annähert, hört der Beobachter einen höheren Ton als bei stehendem Wagen. Entfernt sich der Rettungswagen, so wird ein tieferer Ton wahrgenommen.
Den gleichen Effekt stellt man auch bei einem Autorennen fest. Die Frequenzänderungen und der „Sound” sind dabei um so deutlicher, je schneller die Autos fahren.
$\text{Beispiel 2:}$
Einige Eigenschaften dieses noch aus dem Physikunterricht bekannten Effekts sollen nun anhand von Bildschirmabzügen einer früheren Version des vorliegenden Applets dargestellt werden, wobei natürlich die dynamischen Programmeigenschaften verloren gehen.
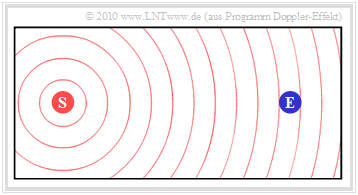
Die erste Grafik zeigt die Ausgangssituation:
- Der ruhende Sender $\rm (S)$ gibt die konstante Frequenz $f_{\rm S}$ ab.
- Die Wellenausbreitung ist in der Grafik durch konzentrische Kreise um $\rm (S)$ veranschaulicht.
- Beim ebenfalls ruhenden Empfänger $\rm (E)$ kommt dann natürlich die Frequenz $f_{\rm E} = f_{\rm S}$ an.
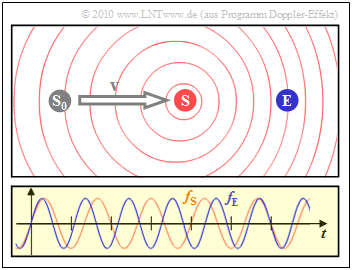
$\text{Beispiel 3:}$ Bei diesem Schnappschuss hat sich der Sender $\rm (S)$ mit konstanter Geschwindigkeit $v$ von seinem Startpunkt $\rm (S_0)$ auf den Empfänger $\rm (E)$ zu bewegt.
- Das rechte Diagramm zeigt, dass die vom Empfänger wahrgenommene Frequenz $f_{\rm E}$ (blaue Schwingung) um etwa $20\%$ größer ist als die Frequenz $f_{\rm S}$ am Sender (rote Schwingung).
- Aufgrund der Bewegung des Senders sind nun die Kreise nicht mehr konzentrisch.
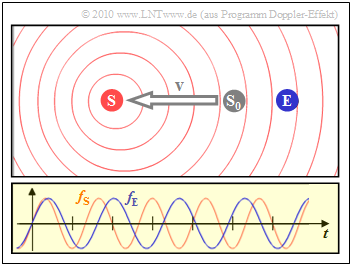
- Das linke Szenerio ergibt sich, wenn sich der Sender $\rm (S)$ vom Empfänger $\rm (E)$ entfernt:
- Dann ist die Empfangsfrequenz $f_{\rm E}$ (blaue Schwingung) um etwa $20\%$ kleiner als die Sendefrequenz $f_{\rm S}$.
Dopplerfrequenz als Funktion von Geschwindigkeit und Winkel der Verbindungslinie
Wir vereinbaren: Gesendet wird die Frequenz $f_{\rm S}$ und empfangen die Frequenz $f_{\rm E}$. Als Dopplerfrequenz bezeichnet man die Differenz $f_{\rm D} = f_{\rm E} - f_{\rm S}$ aufgrund der Relativbewegung zwischen Sender (Quelle) und Empfänger (Beobachter).
- Eine positive Dopplerfrequenz $(f_{\rm E} > f_{\rm S})$ ergibt sich dann, wenn sich Sender und Empfänger (relativ) aufeinander zu bewegen.
- Eine negative Dopplerfrequenz $(f_{\rm E} < f_{\rm S})$ bedeutet, dass sich Sender und Empfänger (direkt oder unter einem Winkel) voneinander entfernen.
Die exakte Gleichung für die Empfangsfrequenz $f_{\rm E}$ unter Einbeziehung eines Winkels $\alpha$ zwischen Bewegungsrichtung und der Verbindungslinie Sender–Empfänger lautet:
- \[f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c \cdot \cos(\alpha)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\text{ Exakte Gleichung}}.\]
Hierbei bezeichnet $v$ die Relativgeschwindigkeit zwischen Sender und Empfänger, während $c = 3 \cdot 10^8 \, {\rm m/s}$ die Lichtgeschwindigkeit angibt.
- Die Grafiken im $\text{Beispiel 3}$ gelten für die unrealistisch große Geschwindigkeit $v = c/5 = 60000\, {\rm km/s}$, die zu den Dopplerfrequenzen $f_{\rm D} = \pm 0.2\cdot f_{\rm S}$ führen.
- Beim Mobilfunk sind die Abweichungen zwischen $f_{\rm S}$ und $f_{\rm E}$ dagegen meist nur ein Bruchteil der Sendefrequenz. Bei solchen realistischen Geschwindigkeiten $(v \ll c)$ kann man von der folgenden Näherung ausgehen, bei der die durch die Relativitätstheorie beschriebenen Effekte unberücksichtigt bleiben:
- \[f_{\rm E} \approx f_{\rm S} \cdot \big [1 +{v}/{c} \cdot \cos(\alpha) \big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\text{ Näherung}}\hspace{0.05cm}.\]
$\text{Beispiel 4:}$ Wir gehen hier von einem festen Sender aus. Der Empfänger nähert sich dem Sender unter dem Winkel $\alpha = 0$.
Untersucht werden sollen verschiedene Geschwindigkeiten:
- eine unrealistisch große Geschwindigkeit $v_1 = 0.6 \cdot c = 1.8 \cdot 10^8 \ {\rm m/s}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_1/c = 0.6$,
- die Maximalgeschwindigkeit $v_2 = 3 \ {\rm km/s} \ \ (10800 \ {\rm km/h})$ bei unbemanntem Testflug $\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_2/c = 10^{-5}$,
- etwa die Höchstgeschwindigkeit $v_3 = 30 \ {\rm m/s} = 108 \ \rm km/h$ auf Bundesstraßen $\hspace{0.3cm}\Rightarrow\hspace{0.3cm}v_3/c = 10^{-7}$.
(1) Nach der exakten, relativistischen ersten Gleichung gilt:
- $$f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 - v/c } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot \left [ \frac{\sqrt{1 - (v/c)^2} }{1 - v/c } - 1 \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - (v/c)^2} }{1 - v/c } - 1 \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_1/c = 0.6\text{:}\hspace{0.5cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - 0.6^2} }{1 - 0.6 } - 1 = \frac{0.8}{0.4 } - 1 \hspace{0.15cm} \underline{ = 1} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E} }/{f_{\rm S} } = 2 \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_2/c = 10^{\rm -5}\text{:}\hspace{0.5cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - (10^{-5})^2} }{1 - (10^{-5}) } - 1 \approx 1 + 10^{-5} - 1 \hspace{0.15cm} \underline{ = 10^{-5} } \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E} }/{f_{\rm S} } = 1.00001 \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_3/c = 10^{\rm -7}\text{:}\hspace{0.5cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - (10^{-7})^2} }{1 - (10^{-7}) } - 1 \approx 1 + 10^{-7} - 1 \hspace{0.15cm} \underline{ = 10^{-7} } \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E} }/{f_{\rm S} } = 1.0000001 \hspace{0.05cm}.$$
(2) Dagegen gilt nach der Näherung, also ohne Berücksichtigung der Relativitätstheorie:
- $$f_{\rm E} = f_{\rm S} \cdot \big [ 1 + {v}/{c} \big ] \Rightarrow \hspace{0.3cm}{f_{\rm D} }/{f_{\rm S} } = {v}/{c} \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_1/c = 0.6\text{:}\hspace{0.7cm} f_{\rm D}/f_{\rm S} \ \underline {= \ 0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.6,$$
- $$\Rightarrow\hspace{0.3cm}v_2/c = 10^{-5}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ 10^{-5} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.00001,$$
- $$\Rightarrow\hspace{0.3cm}v_3/c = 10^{-7}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ 10^{-5} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 1.0000001.$$
$\text{Fazit:}$
- Für „kleine” Geschwindigkeiten liefert die Näherung bis hin zur Genauigkeit eines Taschenrechners das gleiche Ergebnis wie die relativistische Gleichung.
- Die Zahlenwerte zeigen, dass wir auch die Geschwindigkeit $v_2 = \ 10800 \ {\rm km/h}$ in dieser Hinsicht noch als „klein” bewerten können.
$\text{Beispiel 5:}$ Es gelten die gleichen Voraussetzungen wie im letzten Beispiel mit dem Unterschied: Nun entfernt sich der Empfänger vom Sender $(\alpha = 180^\circ)$.
(1) Nach der exakten, relativistischen ersten Gleichung gilt mit ${\rm cos}(\alpha) = -1$:
- $$f_{\rm E} = f_{\rm S} \cdot \frac{\sqrt{1 - (v/c)^2} }{1 + v/c } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot \left [ \frac{\sqrt{1 - (v/c)^2} }{1 + v/c } - 1 \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - (v/c)^2} }{1 + v/c } - 1 \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_1/c = 0.6\text{:}\hspace{0.5cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - 0.6^2} }{1 + 0.6 } - 1 = \frac{0.8}{1.6 } - 1 =-0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E} }/{f_{\rm S} } = 0.5 \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_2/c = 10^{\rm -5}\text{:}\hspace{0.5cm}{f_{\rm D} }/{f_{\rm S} } = \frac{\sqrt{1 - (10^{-5})^2} }{1 + (10^{-5}) } - 1 \approx - 10^{-5} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} {f_{\rm E} }/{f_{\rm S} } = 0.99999 \hspace{0.05cm}.$$
(2) Dagegen gilt nach der Näherung, also ohne Berücksichtigung der Relativitätstheorie:
- $$f_{\rm E} = f_{\rm S} \cdot \big [ 1 - {v}/{c} \big ] \Rightarrow \hspace{0.3cm}{f_{\rm D} }/{f_{\rm S} } = - {v}/{c} \hspace{0.05cm}.$$
- $$\Rightarrow\hspace{0.3cm}v_1/c = 0.6\text{:}\hspace{0.7cm} f_{\rm D}/f_{\rm S} \ \underline {= \ 0.6} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.4,$$
- $$\Rightarrow\hspace{0.3cm}v_2/c = 10^{-5}\text{:}\hspace{0.4cm} f_{\rm D}/f_{\rm S} \ = \ - 10^{-5} \ \ \ ⇒ \ \ \ f_{\rm E}/f_{\rm S} = 0.99999.$$
$\text{Fazit:}$
- Die Empfangsfrequenz $f_{\rm E}$ ist nun kleiner als die Sendefrequenz $f_{\rm S}$ und die Dopplerfrequenz $f_{\rm D}$ ist negativ.
- Bei der Näherung unterscheiden sich die Dopplerfrequenzen für die beiden Bewegungsrichtungen nur im Vorzeichen ⇒ $f_{\rm E} = f_{\rm S} \pm f_{\rm D}$.
- Bei der exakten, relativistischen Gleichung ist diese Symmetrie nicht gegeben.
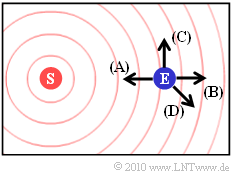
$\text{Beispiel 6:}$ Wie in den vorherigen Beispielen sei der Sender fest. Die Grafik zeigt mögliche Bewegungsrichtungen des Empfängers. Die Richtung $\rm (A)$ wurde im $\text{Beispiel 4}$ betrachtet und die Richtung $\rm (B)$ im $\text{Beispiel 5}$.
(4) Gleichung (2) führt hier zum Ergebnis:
- $$f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm S} \cdot {v_3}/{c} \cdot \cos(\alpha) \hspace{0.05cm}.$$
- Die Fahrtrichtung $\rm (C)$ verläuft senkrecht $(\alpha = 90^\circ)$ zur Verbindungslinie Sender–Empfänger. In diesem Fall tritt keine Dopplerverschiebung auf:
- $$f_{\rm D} \ \underline {= \ 0}.$$
- Die Bewegungsrichtung $\rm (D)$ ist durch $\alpha = \ -135^\circ$ charakterisiert. Daraus resultiert:
- $$f_{\rm D} = 2 \cdot 10^{9}\,\,{\rm Hz} \cdot \frac{30\,\,{\rm m/s <div style="clear:both;"> </div> </div>{3 \cdot 10^{8}\,\,{\rm m/s}} \cdot \cos(-135^{\circ}) \hspace{0.15cm} \underline{ \approx -141\,\,{\rm Hz}} \hspace{0.05cm}.$$
Dopplerfrequenz und deren Verteilung
deutlich kürzen und vereinfachen
Wir fassen die Aussagen der letzten Seite nochmals kurz zusammen, wobei wir von der zweiten, also der nicht–relativistischen Gleichung ausgehen:
- Bei einer Relativbewegung zwischen Sender (Quelle) und Empfänger (Beobachter) kommt es zu einer Verschiebung um die Dopplerfrequenz $f_{\rm D} = f_{\rm E} - f_{\rm S}$.
- Eine positive Dopplerfrequenz $(f_{\rm E} > f_{\rm S})$ ergibt sich dann, wenn sich Sender und Empfänger (relativ) aufeinander zu bewegen. Eine negative Dopplerfrequenz $(f_{\rm E} < f_{\rm S})$ bedeutet, dass sich Sender und Empfänger (direkt oder unter einem Winkel) voneinander entfernen.
- Die maximale Frequenzverschiebung tritt auf, wenn sich Sender und Empfänger direkt aufeinander zu bewegen ⇒ Winkel $\alpha = 0^\circ$. Dieser Maximalwert hängt in erster Näherung von der Sendefrequenz $ f_{\rm S}$ und der Geschwindigkeit $v$ ab $(c = 3 \cdot 10^8 \, {\rm m/s}$ gibt die Lichtgeschwindigkeit an$)$:
- \[f_{\rm D, \hspace{0.05cm} max} = f_{\rm S} \cdot {v}/{c} \hspace{0.05cm}.\]
- Erfolgt die Relativbewegung unter einem beliebigen Winkel $\alpha$ zur Verbindungslinie Sender–Empfänger, so entsteht eine Dopplerverschiebung um
- \[f_{\rm D} = f_{\rm E} - f_{\rm S} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} - \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \le f_{\rm D} \le + \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{0.05cm}.\]
$\text{Fazit:}$ Unter der Annahme gleichwahrscheinlicher Bewegungsrichtungen $($Gleichverteilung für den Winkel $\alpha$ im Bereich $- \pi \le \alpha \le +\pi)$ ergibt sich für die Wahrscheinlichkeitsdichtefunktion $($hier mit „wdf” bezeichnet$)$ der Dopplerfrequenz im Bereich $- f_\text{D, max} \le f_{\rm D} \le + f_\text{D, max}$:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt {1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
Außerhalb des Bereichs zwischen $-f_{\rm D}$ und $+f_{\rm D}$ hat die Wahrscheinlichkeitsdichtefunktion stets den Wert Null.
$\text{Herleitung:}$ Die entstehende Dopplerfrequenz in Abhängigkeit des Bewegungswinkels $\alpha$ lautet:
- \[f_{\rm D} = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha) = g(\alpha) \hspace{0.05cm}.\]
Wir bezeichnen diese Funktion mit $g(\alpha)$ und gehen davon aus, dass
- $\alpha$ alle Winkelwerte zwischen $\pm \pi$ annimmt,
- und zwar mit gleicher Wahrscheinlichkeit ⇒ Gleichverteilung.
Dann ergibt sich für die Wahrscheinlichkeit der Dopplerfrequenz entsprechend dem Kapitel Transformation von Zufallsgrößen im Buch „Stochastische Signaltheorie”:
- \[{\rm wdf}(f_{\rm D})=\frac{ {\rm wdf}(\alpha)}{\vert g\hspace{0.08cm}'(\alpha)\vert}\Bigg \vert_{\hspace{0.1cm} \alpha=h(f_{\rm D})} \hspace{0.05cm}\]
Verwendet sind hier
- die Ableitung $g\hspace{0.08cm}'(\alpha)= - f_\text{D, max} \cdot \sin(\alpha)$, und
- die Umkehrfunktion $ \alpha = h(f_{\rm D})$.
Im Beispiel lautet die Umkehrfunktion:
- $$ \alpha = \arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}).$$
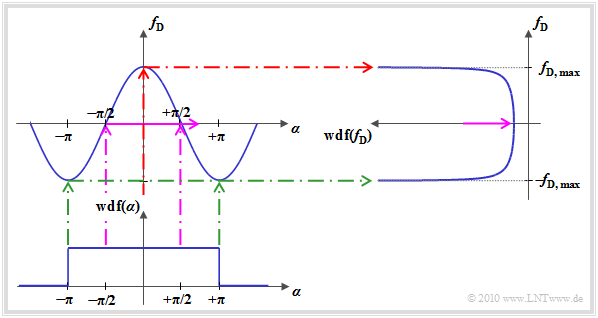
Die Grafik veranschaulicht den Rechengang zur Bestimmung der Dopplerfrequenz–WDF:
- Da die Kennlinie zwischen der Dopplerfrequenz $f_{\rm D}$ und dem Winkel $\alpha$ ⇒ $ g(\alpha) = f_{\rm D, \hspace{0.05cm} max} \cdot \cos(\alpha)$ auf den Wert $f_{\rm D, \hspace{0.05cm} max}$ begrenzt ist, ist für $f_{\rm D}$ kein Wert außerhalb dieses Bereichs möglich.
- Bei der Transformation von Zufallsgrößen muss zwischen Bereichen mit positiver und negativer Steigung der Transformationskennlinie unterschieden werden. Die $\alpha$–Werte zwischen $-\pi$ und $0$ $($positive Steigung der Transformationskennlinie$)$zwischen der Dopplerfrequenz $f_{\rm D}$ und dem Winkel $\alpha$ liefern das Ergebnis
- \[{\rm wdf}(f_{\rm D})=\frac{1/(2\pi)}{f_{\rm D, \hspace{0.05cm} max} \cdot \sin(\alpha)} \Bigg \vert_{\hspace{0.1cm} \alpha=\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})} = \frac{(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} )^{-1} }{ \sin(\arccos(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max}))} = \frac{1}{2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Aus Symmetriegründen trägt der positive $\alpha$–Bereich in gleicher Weise bei, so dass im inneren Bereich insgesamt gilt:
- \[{\rm wdf}(f_{\rm D}) = \frac{1}{\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot \sqrt { 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 } } \hspace{0.05cm}.\]
- Winkel im Bereich um $\alpha = \pm \pi/2$ führen zu einer kleinen Dopplerfrequenz ⇒ $f_{\rm D} \approx 0$ $($violette Markierung$)$. Aufgrund der relativ großen Steigung der cosinusförmigen Kennlinie $g(\alpha)$ bei $\alpha = \pm \pi/2$ ist der WDF–Wert bei $f_{\rm D} \approx 0$ allerdings sehr klein.
- Kleine Winkel $($um $\alpha \approx 0)$ führen dagegen zur maximalen Dopplerfrequenz ⇒ $f_{\rm D} \approx f_{\rm D, \hspace{0.05cm} max}$ $($rote Markierung$)$. Aufgrund der nahezu horizontalen Kennlinie $g(\alpha)$ ist hier die $f_{\rm D}$–WDF deutlich größer. Für $f_{\rm D} \equiv f_{\rm D, \hspace{0.05cm} max}$ ergibt sich sogar ein unendlich großer Wert.
- Winkel um $\alpha = \pm \pi$ führen dagegen zur Dopplerfrequenz $f_{\rm D} \approx -f_{\rm D, \hspace{0.05cm} max}$ $($grüne Markierung$)$. Auch hier ist die Kennlinie nahezu horizontal und es ergibt sich wiederum ein großer WDF–Wert.
AKF und LDS bei Rayleigh–Fading
deutlich kürzen und vereinfachen
Die statistischen Bindungen innerhalb der reellen „Signale” $x(t)$ und $y(t)$ bzw. innerhalb der komplexen Größe $z(t)$ sind auf den Dopplereffekt zurückzuführen.
Wir setzen nun eine in alle Richtungen gleich abstrahlende Antenne voraus. Dann ist das Doppler–LDS formgleich mit der WDF der Dopplerfrequenzen.
Für ${\it \Phi}_x(f_{\rm D})$ muss die WDF noch mit der Leistung $\sigma^2$ des Gaußprozesses multipliziert werden, und für das resultierende LDS ${\it \Phi}_z(f_{\rm D})$ des komplexen Faktors $z(t) = x(t) + {\rm j} \cdot y(t) $ gilt nach Verdoppelung:
- \[{\it \Phi}_z(f_{\rm D}) = \left\{ \begin{array}{c} (2\sigma^2)/( \pi \cdot f_{\rm D, \hspace{0.05cm} max}) \cdot \left [ 1 - (f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2 \right ]^{-0.5} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} |f_{\rm D}| \le f_{\rm D, \hspace{0.05cm} max} \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.\]
Man nennt diesen Verlauf nach William C. Jakes Jr. das Jakes–Spektrum. Die Verdoppelung ist notwendig, da bisher nur der Beitrag des Realteils $x(t)$ betrachtet wurde.
Die zugehörige Autokorrelationsfunktion (AKF) erhält man nach Fourierrücktransformation:
- \[\varphi_z ({\rm \Delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \Delta}t)\hspace{0.05cm},\]
mit der Besselfunktion erster Art und nullter Ordnung (erste Gleichung: Definition, zweite Gleichung: Reihenentwicklung):
- \[{\rm J }_0 (u) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{- {\rm j }\hspace{0.03cm}\cdot \hspace{0.03cm}u \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} = \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(-1)^k \cdot (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
Die Zahlenwerte dieser Funktion erhalten Sie mit dem gleichnamigen Applet.
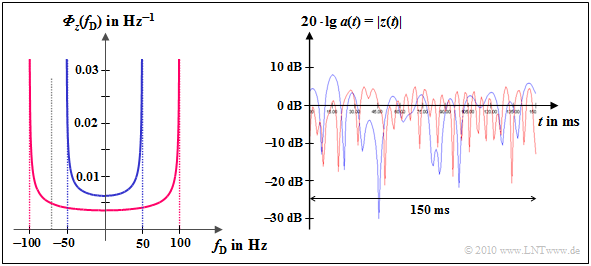
$\text{Beispiel 4:}$ Links dargestellt ist das Jakes–Spektrum
- für $f_{\rm D, \hspace{0.05cm} max} = 50 \ \rm Hz$ (blaue Kurve) bzw.
- für $f_{\rm D, \hspace{0.05cm} max} = 100 \ \rm Hz$ (rote Kurve).
Beim GSM–D–Netz $(f_{\rm S} = 900 \ \rm MHz)$ entsprechen diese Werte den Geschwindigkeiten $v = 60 \ \rm km/h$ bzw. $v = 120 \ \rm km/h$.
Beim E–Netz $(f_{\rm S} = 1.8 \ \rm GHz)$ gelten diese Werte für halb so große Geschwindigkeiten: $v = 30 \ \rm km/h$ bzw. $v = 60 \ \rm km/h$.
Das rechte Bild zeigt den logarithmierten Betrag von $z(t)$:
- Man erkennt das doppelt so schnelle Fading des roten Kurvenverlaufs.
- Die Rayleigh–WDF (Amplitudenverteilung) ist unabhängig von $f_{\rm D, \hspace{0.05cm} max}$ und deshalb für beide Fälle gleich.
Versuchsdurchführung
Eventuell noch überarbeiten
- Wählen Sie zunächst die Nummer 1 ... 10 der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
- In den folgenden Aufgabenbeschreibungen und Musterlösungen sind die Frequenzen $f_{\rm S}$, $f_{\rm E}$ und $f_{\rm D}$ jeweils auf die Bezugsfrequenz $f_{\rm 0}$ normiert.
bis hierher
AS: Für (1) gilt auch $S_x=150,\ S_y=200,\ \varphi=0$
(1) Zunächst betrachten wir die relativistische Einstellung „Exakt”. Der Sender bewegt sich stets mit Geschwindigkeit $v/c = 0.8$ und die Sendefrequenz sei $f_{\rm S}= 1$.
Welche Empfangsfrequenzen $f_{\rm E}$ ergeben sich bei beiden Bewegungsrichtungen? Wie groß ist jeweils die Dopplerfrequenz $f_{\rm D}$?
- Wenn sich der Sender unter dem Winkel $\varphi=0^\circ$ dem Empfänger annähert, ergibt sich die Empfangsfrequenz $f_{\rm E}= 3$ ⇒ Dopplerfrequenz $f_{\rm D}= f_{\rm E} - f_{\rm S}= 2$.
- Entfernt sich der Sender vom Empfänger $($z.B. für $\varphi=0^\circ$, wenn er diesen überholt, oder für $\varphi=180^\circ)$, dann gilt $f_{\rm E}= 0.333$ ⇒ $f_{\rm D}= f_{\rm E} - f_{\rm S}= -0.667$.
- Das gleiche Ergebnis erhält man bei ruhendem Sender und sich bewegendem Empfänger: Kommen sich beide näher, dann gilt $f_{\rm D}= 2$, ansonsten $f_{\rm D}= -0.667$.
(2) Die Einstellungen bleiben weitgehend erhalten. Wie ändern sich sich die Ergebnisse gegenüber (1) mit der Sendefrequenz $f_{\rm S}= 1.5$?
Tipp für eine möglichst zeitsparende Versuchsdurchführung: Schalten Sie abwechselnd zwischen den Fahrtrichtungen „Rechts” und „Links” hin und her.
- Bewegungsrichtung $\varphi=0^\circ$: Empfangsfrequenz $f_{\rm E}= 4.5$ ⇒ Dopplerfrequenz $f_{\rm D}= f_{\rm E} - f_{\rm S}= 3$. Aber: $f_{\rm E}/f_{\rm S}= 3$, $f_{\rm D}/f_{\rm S}= 2$ ⇒ Beides wie in (1).
- Bewegungsrichtung $\varphi=180^\circ$: Empfangsfrequenz $f_{\rm E}= 0.5$ ⇒ Dopplerfrequenz $f_{\rm D}= -1$. Aber: $f_{\rm E}/f_{\rm S}= 0.333$, $f_{\rm D}/f_{\rm S}= -0.667$ ⇒ Beides wie in (1).
AS: Für (3) gilt auch $S_x=300,\ S_y=200,\ \varphi=0$
(3) Wir betrachten weiter die relativistische Einstellung „Exakt”. Der Sender bewegt sich nun mit Geschwindigkeit $v/c = 0.4$ und die Sendefrequenz sei $f_{\rm S}= 2$.
Welche Frequenzen $f_{\rm E}$ und $f_{\rm E}$ ergeben sich bei beiden Bewegungsrichtungen? Wählen Sie wieder abwechselnd „Rechts” bzw. „Links”.
- Bewegungsrichtung $\varphi=0^\circ$: Empfangsfrequenz $f_{\rm E}= 3.055$ ⇒ Dopplerfrequenz $f_{\rm D}= f_{\rm E} - f_{\rm S}= 1.055$. ⇒ $f_{\rm E}/f_{\rm S}= 1.528$, $f_{\rm D}/f_{\rm S}= 0.528$.
- Bewegungsrichtung $\varphi=180^\circ$: Empfangsfrequenz $f_{\rm E}= 1.309$ ⇒ Dopplerfrequenz $f_{\rm D}= -0.691$. ⇒ $f_{\rm E}/f_{\rm S}= 0.655$, $f_{\rm D}/f_{\rm S}= -0.346$.
(4) Es gelten weiter die bisherigen Voraussetzungen, aber nun die nicht–relativistische Einstellung „Näherung”. Welche Unterschiede ergeben sich gegenüber (3)?
- Bewegungsrichtung $\varphi=0^\circ$: Empfangsfrequenz $f_{\rm E}= 2.8$ ⇒ Dopplerfrequenz $f_{\rm D}= f_{\rm E} - f_{\rm S}= 0.8$ ⇒ $f_{\rm E}/f_{\rm S}= 1.4$, $f_{\rm D}/f_{\rm S}= 0.4$.
- Bewegungsrichtung $\varphi=180^\circ$: Empfangsfrequenz $f_{\rm E}= 1.2$ ⇒ Dopplerfrequenz $f_{\rm D}= -0.8$. ⇒ $f_{\rm E}/f_{\rm S}= 0.6$, $f_{\rm D}/f_{\rm S}= -0.4$.
- Mit der „Näherung” ergeben sich für beide $f_{\rm D}$ gleiche Zahlenwerte mit verschiedenen Vorzeichen. Bei der exakten Gleichung ist diese Symmetrie nicht gegeben.
(5) Es gelte weiterhin $f_{\rm S}= 2$. Bis zu welcher Geschwingkeit $(v/c)$ ist der relative Fehler zwischen Näherung und exaktem Wert betragsmäßig kleiner als $5\%$?
- Mit $v/c =0.08$ erhält man für die Dopplerfrequenzen nach der exakten Gleichung $f_{\rm D}= 0.167$ bzw. $f_{\rm D}= -0.154$ und nach der Näherung $f_{\rm D}= \pm0.16$.
- Dementsprechend ist die relative Abweichung „(Näherung – Exakt)/Exakt)” gleich $0.16/0.167-1=-4.2\%$ bzw. $(-0.16)/(-0.154)-1=+3.9\%$.
- Mit $v/c =0.1$ sind die Abweichungen betragsmäßig $>5\%$. Für $v < c/10 = 30\hspace{0.05cm}000$ km/s ist aber die Dopplerfrequenz–Näherung ausreichend.
Dummy
AS: Für (6) gilt auch $S_x=300,\ S_y=50,\ \varphi=-45$ Oder $\varphi=+45$?
(6) Hier und in den nachfolgenden Aufgaben soll gelten: $f_{\rm S}= 1$, $v/c= 0.4$ ⇒ $f_{\rm D} = f_{\rm S} \cdot v/c \cdot \cos(\alpha)$. Mit $\cos(\alpha) = \pm 1$: $f_{\rm D}/f_{\rm S} =\pm 0.4$.
Welche normierten Dopplerfrequenzen ergeben sich mit dem eingestellten Startkoordinaten $(300,\ 50)$ und der Bewegungsrichtung $\varphi=-45^\circ$?
- Ausgehend vom Startpunkt $(300,\ 50)$ und $\varphi=-45^\circ$ bewegt sich der Sender direkt auf den Empfänger zu $(\alpha=0^\circ)$ oder entfernt sich von ihm $(\alpha=180^\circ)$.
- Es liegt also die gleiche Konstellation vor wie mit dem Startpunkt $(300,\ 200)$ und $\varphi=0^\circ$. Deshalb gilt auch hier für die Dopplerfrequenz: $f_{\rm D}/f_{\rm S} =\pm 0.4$.
(7) Nun liegt der Sender fest etwas oberhalb der Mitte $(300,\ 190),$ der Empfänger bewegt sich horizontal auf halber Höhe $(v/c = 0.4, \hspace{0.3cm}\varphi=0^\circ$ bzw. $\varphi=180^\circ)$.
Beobachten und interpretieren Sie die zeitliche Änderung der Dopplerfrequenz $f_{\rm D}$.
- Wie in der Aufgabe (6) sind auch hier nur Werte zwischen $f_{\rm D}=0.4$ und $f_{\rm D}=-0.4$ möglich, aber nun alle Zwischenwerte im Bereich $-0.4 \le f_{\rm D} \le +0.4$.
- Wie Sie mit dem Button „Step” zeigen können, kommt der Dopplerwert $f_{\rm D}=0$ nur vor, wenn der Empfänger genau unterhalb des Senders liegt $(\alpha=\pm 90^\circ)$.
- Dagegen sind Dopplerfrequenzen an den beiden Rändern $(|f_{\rm D}| = 0.4 -\varepsilon$, wobei $\varepsilon$ eine kleine positive Größe angibt$)$, sehr viel häufiger.
- Schon aus diesem Versuch wird der prinzipielle Verlauf von Doppler–WDF und Doppler–LDS ⇒ „Jakes–Spektrum” erklärbar.
(8) Was ändert sich, wenn der Sender bei sonst gleichen Einstellungen fest am oberen Rand der Grafikfläche in der Mitte liegt $(300,\ 400) $?
- Die Dopplerwerte $f_{\rm D} \approx0$ werden häufiger, solche an den Rändern seltener. Aufgrund der begrenzten Zeichenfläche gibt es keine Werte $|f_{\rm D}| > 0.325$.
Zur Handhabung des Applets
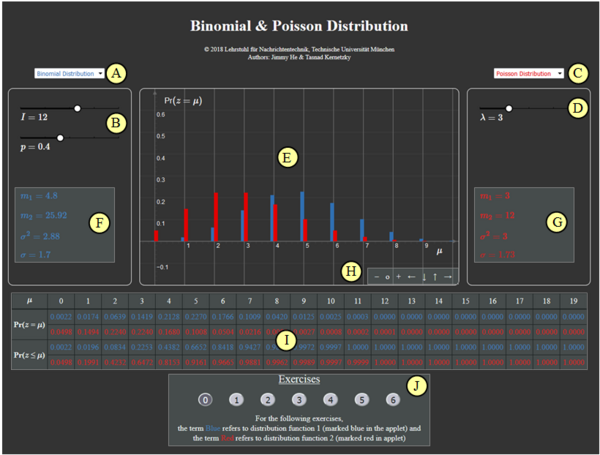
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2005 von Bettina Hirner im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Andre Schulz (Bachelorarbeit LB, Betreuer: Benedikt Leible und Tasnád Kernetzky ) unter „HTML5” neu gestaltet.