Kanalcodierung/Grundlegendes zu den Turbocodes: Unterschied zwischen den Versionen
| Zeile 162: | Zeile 162: | ||
*Bei kleinen Abszissenwerten ist der Kurvenabfall in der gewählten Darstellung nahezu linear und ausreichend steil. Für ${\rm Pr(Bitfehler)} = 10^{–5}$ benötigt man $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.<br> | *Bei kleinen Abszissenwerten ist der Kurvenabfall in der gewählten Darstellung nahezu linear und ausreichend steil. Für ${\rm Pr(Bitfehler)} = 10^{–5}$ benötigt man $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.<br> | ||
| − | *Im Vergleich zur [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalkapazit.C3.A4t_des_AWGN.E2.80.93Modells_.282.29| Shannon–Grenze]], die sich für die Coderate $R = 1/3$ zu $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.<br> | + | *Im Vergleich zur [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalkapazit.C3.A4t_des_AWGN.E2.80.93Modells_.282.29| Shannon–Grenze]], die sich für die Coderate $R = 1/3$ zu $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.<br> |
*Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.<br><br> | *Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.<br><br> | ||
Version vom 28. November 2017, 17:36 Uhr
Inhaltsverzeichnis
- 1 Grundstruktur eines Turbocodes (1)
- 2 Grundstruktur eines Turbocodes (2)
- 3 Erste Voraussetzung für Turbocodes: Rekursive Komponentencodes
- 4 Zweite Voraussetzung für Turbocodes: Interleaving
- 5 Symbolweise iterative Decodierung eines Turbocodes
- 6 Leistungsfähigkeit der Turbocodes (1)
- 7 Leistungsfähigkeit der Turbocodes (2)
- 8 Seriell verkettete Turbocodes – SCCC
- 9 Einige Anwendungsgebiete für Turbocodes
- 10 Aufgaben
- 11 Quellenverzeichnis
Grundstruktur eines Turbocodes (1)
Alle heute (2016) aktuellen Kommunikationssysteme wie UMTS (3. Mobilfunkgeneration) und LTE (4. Mobilfunkgeneration) verwenden das in Kapitel 4.1 dargelegte Konzept der symbolweisen iterativen Decodierung. Dass dies so ist, steht unmittelbar mit der Erfindung der Turbocodes im Jahre 1993 durch C. Berrou, A. Glavieux und P. Thitimajshima in Zusammenhang, denn erst mit diesen Codes konnte man sich der Shannon–Grenze mit vertretbarem Decodieraufwand annähern.
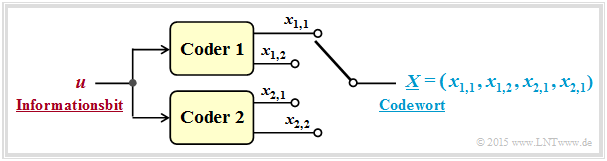
Turbocodes ergeben sich durch die parallele oder serielle Verkettung von Faltungscodes. Die Grafik zeigt die parallele Verkettung zweier Codes mit den Parametern $k = 1, \ n = 2$ ⇒ Rate $R = 1/2$.
In dieser Darstellung bezeichnet:
- $u$ das aktuell betrachtete Bit der Informationssequenz $\underline{u}$,
- $x_{i,j}$ das aktuell betrachtete Bit am Ausgang $j$ von Coder $i$ (mit $1 ≤ i ≤ 2, \ 1 ≤ j ≤ 2)$,
- $\underline{X} = (x_{1,1}, \ x_{1,2}, \ x_{2,1}, \ x_{2,2})$ das Codewort für das aktuelle Informationsbit $u$.
Die resultierende Rate des verketteten Codiersystems ist somit $R = 1/4$.
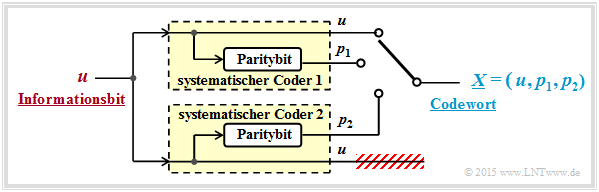
Verwendet man systematische Komponentencodes, so ergibt sich das folgende Modell:
Die Modifikationen gegenüber der oberen Grafik lassen sich wie folgt begründen:
- Bei systematischen Codes $C_1$ und $C_2$ ist sowohl $x_{1,1} = u$ als auch $x_{2,1} = u$. Deshalb kann man auf die Übertragung eines redundanten Bits (zum Beispiel $x_{2,2}$) verzichten.
- Mit dieser Reduktion ergibt sich ein Rate–1/3–Turbocode mit den Parametern $k = 1$ und $n = 3$. Das Codewort lautet mit den Paritybits $p_1$ und $p_2$ von Coder 1 bzw. Coder 2:
- \[\underline{X} = \left (u, p_1, p_2 \right )\hspace{0.05cm}.\]
Auf der nächsten Seite wird unser Turbocode–Modell nochmals geringfügig modifiziert.
Grundstruktur eines Turbocodes (2)
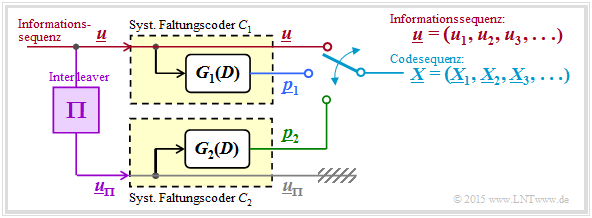
Im Folgenden gehen wir stets von einem noch weiter modifizierten Turbocoder–Modell aus:
- Wie es für die Beschreibung von Faltungscodes erforderlich ist, liegt nun am Eingang anstelle des isolierten Informationsbits $u$ die Informationssequenz $\underline{u} = (u_1, \ u_2, \ ... , \ u_i , \ ...)$ an.
- Die Codewortsequenz wird mit $\underline{x} = (\underline{X}_1, \underline{X}_2, \ ... , \ \underline{X}_i, \ ...)$ bezeichnet. Um Verwechslungen zu vermeiden, wurden vorne die Codeworte $\underline{X}_i = (u, \ p_1, \ p_2)$ mit Großbuchstaben eingeführt.
- Die Coder $C_1$ und $C_2$ werden (gedanklich) als Digitale Filter konzipiert und sind somit durch die Übertragungsfunktionen $G_1(D)$ und $G_2(D)$ darstellbar.
- Aus verschiedenen Gründen ⇒ siehe übernächste Seite sollte die Eingangssequenz des zweiten Coders ⇒ $\underline{u}_{\pi}$ gegenüber der Sequenz $\underline{u}$ durch einen Interleaver $(\Pi)$ verwürfelt sein.
- Somit spricht nichts dagegen, die beiden Coder gleich zu wählen: $G_1(D) = G_2(D) = G_3(D)$. Ohne Interleaver würde dies die Korrekturfähigkeit extrem einschränken.
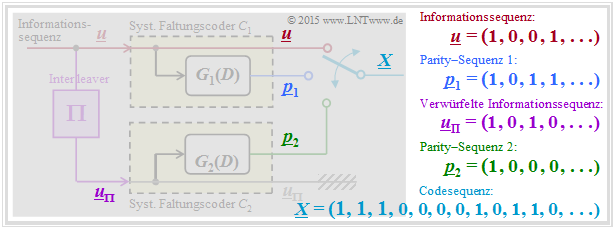
- Für $\underline{u}_{\pi}$ ist eine $3×4$–Interleaver–Matrix entsprechend Aufgabe Z4.8 berücksichtigt.
- Die Paritysequenzen ergeben sich gemäß $G_1(D) = G_2(D) = 1 + D^2$ ⇒ siehe Aufgabe A4.8.
Erste Voraussetzung für Turbocodes: Rekursive Komponentencodes
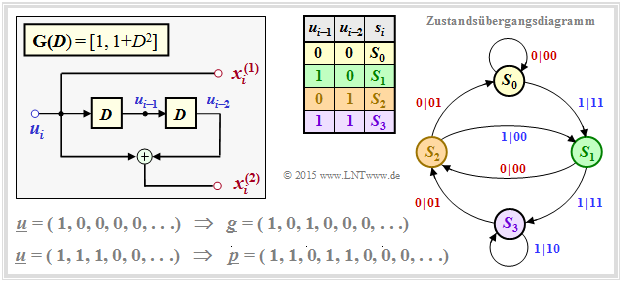
Nichtrekursive Übertragungsfunktionen zur Erzeugung der Paritysequenzen bewirken einen Turbocode mit unzureichend kleiner Minimaldistanz. Grund für diese Unzulänglichkeit ist die endliche Impulsantwort $\underline{g} = (1, \ g_2, \ ... , \ g_m, \ 0, \ 0, \ ...)$ mit $g_2, \ ... , \ g_m ∈ \{0, 1\}$. Hierbei bezeichnet $m$ das Codegedächtnis.
Die Grafik zeigt das Zustandsübergangsdiagramm für das Beispiel $\mathbf{G}(D) = [1, \ 1 + D^2]$. Die Übergänge sind mit „$u_i|u_i p_i$” beschriftet. Die Abfolge $S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \ ... \ $ führt bezüglich des Eingangs zur Informationssequenz $\underline{u} = (1, 0, 0, 0, 0, \ ...)$ und bezüglich des jeweils zweiten Codesymbols zur Paritysequenz $\underline{p} = (1, 0, 1, 0, 0, \ ...)$ ⇒ identisch mit der Impulsantwort $\underline{g}$ ⇒ Gedächtnis $m = 2$.
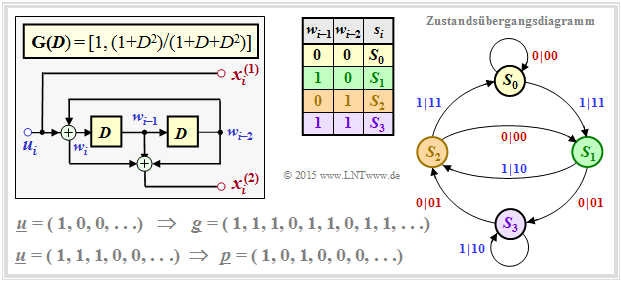
Die untere Grafik gilt für einen sog. RSC–Code (Recursive Systematic Convolutional) entsprechend $\mathbf{G}(D) = [1, \ (1+ D^2)/(1 + D + D^2)]$. Hier führt die Folge $S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → \ ... \ $ zur Impulsantwort $\underline{g} = (1, 1, 1, 0, 1, 1, 0, 1, 1, \ ...)$. Diese Impulsantwort setzt sich aufgrund der Schleife $S_1 → S_3 → S_2 → S_1$ bis ins Unendliche fort. Dies ermöglicht bzw. erleichtert die iterative Decodierung.
Mehr Details zu den Beispielen auf dieser Seite finden Sie in Aufgabe A4.8 und Aufgabe A4.9.
Zweite Voraussetzung für Turbocodes: Interleaving
Es ist offensichtlich, dass bei $G_1(D) = G_2(D)$ ein Interleaver $(\Pi)$ unerlässlich ist. Ein weiterer Grund ist, dass die Apriori–Information als unabhängig vorausgesetzt wird. Somit sollten benachbarte (und somit möglicherweise stark abhängige) Bits für den jeweils anderen Teilcode weit auseinander liegen.
Für jeden RSC–Code ⇒ unendliche Impulsantwort $\underline{g}$ ⇒ gebrochen–rationale Übertragungsfunktion $G(D)$ gibt es nämlich gewisse Eingangssequenzen $\underline{u}$, die zu sehr kurzen Paritysequenzen $\underline{p} = \underline{u} ∗ \underline{g}$ mit geringem Hamming–Gewicht $w_{\rm H}(\underline{p})$ führen. Eine solche Sequenz ist beispielsweise in der unteren Grafik auf der letzten Seite angegeben: $\underline{u} = (1, 1, 1, 0, 0, \ ...)$. Dann gilt für die Ausgangssequenz:
\[P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2\]
\[\Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm})\hspace{0.05cm}. \]
Durch Interleaving (deutsch: Verwürfelung) wird nun mit großer Wahrscheinlichkeit sichergestellt, dass diese Sequenz $\underline{u} = (1, 1, 1, 0, 0, \ ...)$ in eine Sequenz $\underline{u}_{\pi}$ gewandelt wird,
- die zwar ebenfalls nur drei Einsen beinhaltet,
- deren Ausgangssequenz aber durch ein großes Hamming–Gewicht $w_{\rm H}(\underline{p})$ gekennzeichnet ist.
Somit gelingt es dem Decoder, solche „Problemsequenzen” iterativ aufzulösen.
Zur Beschreibung der Interleaver verwendet man die Zuordnung $I_{\rm In} → I_{\rm Out}$. Diese Bezeichnungen stehen für die Indizes von Ausgangs– bzw. Eingangsfolge. Die Interleavergröße wird mit $I_{\rm max}$ benannt.
Es gibt mehrere, grundsätzlich verschiedene Interleaver–Konzepte:
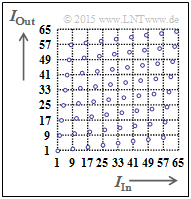
Bei einem Block–Interleaver füllt man eine Matrix mit $S$ Spalten und $Z$ Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit $I_{\rm max} = S \cdot Z \ \rm Bit$ deterministisch verwürfelt.
Die Grafik verdeutlicht das Prinzip für $I_{\rm max} = 64$ ⇒ $1 ≤ I_{\rm In} < 65$ und $1 ≤ I_{\rm Out} < 65$. Die Reihenfolge der Ausgangsbits lautet dann:
- $$1, 9, 17, 25, 33, 41, 49, 57, 2, 10, 18, \ ... , 48, 56, 64.$$
Mehr Informationen zum Block–Interleaving gibt es in Aufgabe Z4.8.
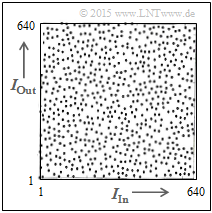
Turbocodes verwenden oft den $S$–Random–Interleaver. Dieser pseudozufällige Algorithmus mit dem Parameter „$S$” garantiert, dass zwei am Eingang weniger als $S$ auseinander liegende Indizes am Ausgang mindestens im Abstand $S + 1$ auftreten. Die linke Grafik zeigt die $S$–Random–Kennlinie $I_{\rm Out}(I_{\rm In})$ für $I_{\rm max} = 640$.
Auch dieser Algorithmus ist deterministisch, und man kann die Verwürfelung im Decoder rückgängig machen ⇒ De–Interleaving. Die Verteilung wirkt trotzdem „zufälliger” als bei Block–Interleaving.
Symbolweise iterative Decodierung eines Turbocodes
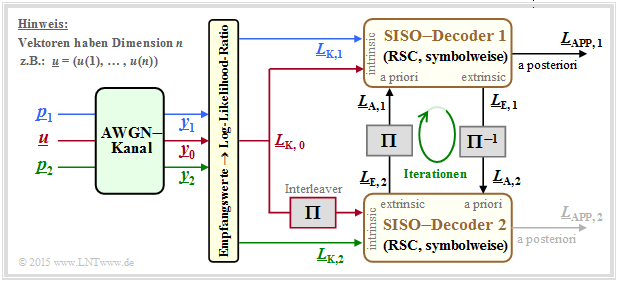
Die Decodierung eines Turbocodes geschieht grundsätzlich wie in Kapitel 4.1 beschrieben. Aus der folgenden Grafik erkennt man aber einige nur für den Turbodecoder zutreffende Besonderheiten.
Vorausgesetzt ist ein Rate–1/3–Turbocode entsprechend der Beschreibung auf der ersten Seite dieses Abschnitts. Auch die Farbgebung für die Informationssequenz $\underline{u}$ und die beiden Paritysequenzen $\underline{p}_1$ und $\underline{p}_2$ sind an die früheren Grafiken angepasst. Weiter ist zu bemerken:
- Die Empfangsvektoren $\underline{y}_0, \underline{y}_1$ und $\underline{y}_2$ sind reellwertig und liefern die jeweilige Soft–Information bezüglich der Sequenzen $\underline{u}$ (Information), $\underline{p}_1$ (Parity für Coder 1) und $\underline{p}_2$ (Parity für Coder 2).
- Der Decoder 1 erhält die erforderliche intrinsische Information in Form der $L$–Werte $L_{\rm K, 0}$ (aus $\underline{y}_0$) und $L_{\rm K,1}$ (aus $\underline{y}_1$) über jedes einzelne Bit der Sequenzen $\underline{u}$ und $\underline{p}_1$.
- Beim zweiten Decoder ist auch die Verwürfelung der Informationssequenz $\underline{u}$ durch den Interleaver zu berücksichtigen. Die zu verarbeitenden $L$–Werte sind somit $\pi(L_{\rm K, 0}$ und $L_{\rm K, 2}$.
- Beim allgemeinen SISO–Decoder am Ende von Kapitel 4.1 wurde der Informationsaustausch zwischen den beiden Komponentendecodern mit $\underline{L}_{\rm A, 2} = \underline{L}_{\rm E, 1}$ sowie $\underline{L}_{\rm A, 1} = \underline{L}_{\rm E, 2}$ angegeben. Ausgeschrieben auf Bitebene bedeuten diese Gleichungen mit $1 ≤ i ≤ n$:
- \[L_{\rm A, \hspace{0.01cm}2}(i) = L_{\rm E, \hspace{0.01cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.01cm}1}(i) = L_{\rm E, \hspace{0.01cm}2}(i) \hspace{0.03cm}.\]
- Beim Turbodecoder muss bei diesem Informationsaustausch auch der Interleaver berücksichtigt werden. Dann gilt wieder für $i = 1, \ ... , \ \pi$:
- \[L_{\rm A, \hspace{0.01cm}2}\left ({\rm \pi}(i) \right ) = L_{\rm E, \hspace{0.01cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.01cm}1}(i) = L_{\rm E, \hspace{0.01cm}2}\left ({\rm \pi}(i) \right ) \hspace{0.05cm}.\]
- Der Aposteriori–$L$–Wert wird in obigem Modell (willkürlich) vom Decoder 1 abgegeben. Dies lässt sich damit begründen, dass eine Iteration für einen zweifachen Informationsaustausch steht.
Leistungsfähigkeit der Turbocodes (1)
Wir betrachten wieder wie auf den letzten Seiten den Rate–1/3–Turbocode
- mit gleichen Filterfunktionen $G_1(D) = G_2(D) = (1 + D^2)/(1 + D + D^2)$ ⇒ Gedächtnis $m = 2$,
- mit der Interleavergröße $K$; zunächst gelte $K = 10000,$
- eine ausreichende Anzahl an Iterationen $(I = 20)$, hier nahezu gleichzusetzen mit „$I → ∞$”.
Die beiden RSC–Komponentencodes sind jeweils auf $K \ \rm Bit$ terminiert. Deshalb gruppieren wir
- die Informationssequenz $\underline{u}$ zu Blöcken mit je $K$ Informationsbits, und
- die Codesequenz $\underline{x}$ zu Blöcken mit je $N = 3 \cdot K$ Codebits.
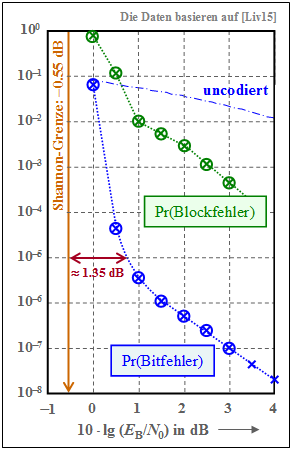
Die Grafik zeigt als grüne Kurve in doppelt–logarithmischer Darstellung die Blockfehlerwahrscheinlichkeit ⇒ ${\rm Pr(Blockfehler)}$ beim AWGN–Kanal in Abhängigkeit der Kenngröße $10 \cdot {\rm lg} \, (E_{\rm B}/N_0)$. Man erkennt:
- Die Daten entstammen dem Vorlesungsskript [Liv15][1]. Die mit Kreuzen markierten Punkte ergaben sich aus den Gewichtsfunktionen des Turbocodes mit Hilfe der Union Bound.
- Simulationsergebnisse aus [Liv15] sind in der Grafik durch Kreise markiert. Sie sind nahezu deckungsgleich mit den berechneten Werten.
- Die Union Bound ist nur eine obere Schranke, basierend auf ML–Decodierung. Der iterative Decoder ist suboptimal (also schlecher als ML). Diese beiden Effekte heben sich scheinbar auf.
- Etwa bei $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 1 \ \rm dB$ ist ein Knick im (grünen) Kurvenverlauf festzustellen, der mit der Steigungsänderung von ${\rm Pr(Bitfehler)}$ ⇒ blaue Kurve korrespondiert. Die Erklärung folgt unten.
Die blauen Kreuze (Berechnung) und die blauen Kreise (Simulation) bezeichnen die Bitfehlerwahrscheinlichkeit. Als Vergleichskurve ist die (strichpunktierte) Kurve für uncodierte Übertragung eingezeichnet. Anzumerken ist:
- Bei kleinen Abszissenwerten ist der Kurvenabfall in der gewählten Darstellung nahezu linear und ausreichend steil. Für ${\rm Pr(Bitfehler)} = 10^{–5}$ benötigt man $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.
- Im Vergleich zur Shannon–Grenze, die sich für die Coderate $R = 1/3$ zu $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode (mit Gedächtnis $m = 2$) nur etwa $1.35 \ \rm dB$ entfernt.
- Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (fast) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{–7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.
Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.
Leistungsfähigkeit der Turbocodes (2)
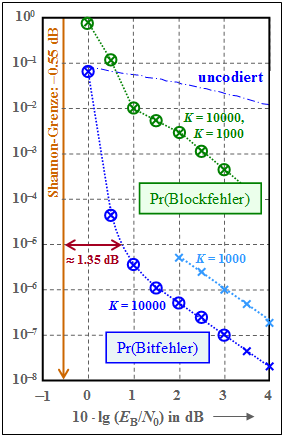
Wir betrachten weiter die (blaue) Bitfehlerwahrscheinlichkeit für die Interleavergröße K = 10000 und versuchen, den flacheren Abfall bei größerem EB/N0 zu erklären. Man spricht von einem Error Floor.
- Der Grund für dieses asymptotisch schlechtere Verhalten bei besserem Kanal (im Beispiel: ab ca. 10 · lg EB/N0 > 2 dB) ist die Periode P der Coderimpulsantwort g, wie auf der Seite Zweite Voraussetzung: Interleaving nachgewiesen.
- Im Beispiel (m = 2) ist die Periode P = 2m = 3. Dadurch ist für u = (1, 1, 1) ⇒ wH(u) = 3 trotz unbegrenzter Impulsantwort g die Paritysequenz begrenzt: p = (1, 0, 1) ⇒ wH(p) = 2.
- Die Sequenz u = (0, ..., 0, 1, 0, 0, 1, 0, ...) ⇒ U(D) = Dx · (1 + DP) führt ebenfalls zu einem kleinen Hamming–Gewicht wH(p) am Ausgang, was den iterativen Decodierprozess erschwert.
- Eine gewisse Abhilfe schafft der Interleaver, der dafür sorgt, dass nicht die beiden Sequenzen p1 und p2 gleichzeitig durch sehr kleine Hamming–Gewichte wH(p1) und wH(p2) belastet sind.
- Aus der Grafik erkennt man, dass Pr(Bitfehler) umgekehrt proportional zur Interleavergröße K ist. Das heißt: Bei großem K funktioniert die Entspreizung ungünstiger Eingangssequenzen besser.
- Allerdings gilt die Näherung K · Pr(Bitfehler) = const. nur für größere EB/N0–Werte ⇒ kleinere Bitfehlerwahrscheinlichkeiten. Der oben beschriebene Effekt tritt zwar auch bei kleinerem EB/N0 auf, doch sind dann die Auswirkungen auf die Bitfehlerwahrscheinlichkeit geringer.
Dagegen gilt der flachere Verlauf der Blockfehlerwahrscheinlichkeit (grüne Kurve weitgehend unabhängig von der Interleavergröße K, also sowohl für K = 1000 als auch für K = 10000. Im Bereich ab 10 · lg EB/N0 > 2 dB dominieren aufgrund der kleinen Bitfehlerwahrscheinlichkeiten (< 10–5) nämlich Einzelfehler, so dass hier die Näherung Pr(Blockfehler) ≈ Pr(Bitfehler) · K gültig ist.
Die hier beispielhaft gezeigten Kurven für Bit– und Blockfehlerwahrscheinlichkeit gelten qualitativ auch für m > 2, zum Beispiel für den Turbocode von UMTS und LTE (jeweils m = 3), der in Aufgabe A4.10 analysiert wird. Es ergeben sich aber einige quantitative Unterschiede:
- Die Kurve verläuft bei kleinem EB/N0 steiler und der Abstand von der Shannongrenze ist etwas geringer als im hier gezeigten Beispiel für m = 2.
- Auch für größeres m gibt es einen Error Floor. Der Knick in den dargestellten Kurven erfolgt aber später, also bei kleineren Fehlerwahrscheinlichkeiten.
Seriell verkettete Turbocodes – SCCC
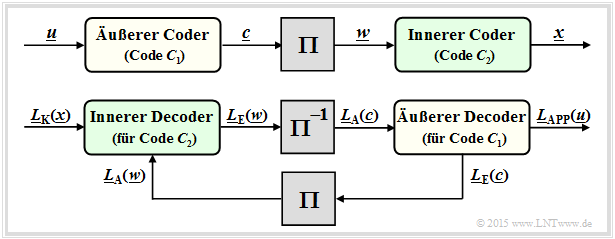
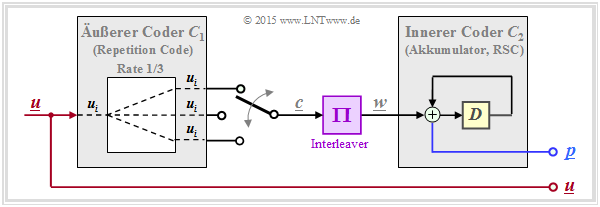
Die bisher betrachteten Turbocodes werden manchmal auch als Parallel Concatenated Convolutional Codes (PCCC) bezeichnet. Einige Jahre nach Berrou's Erfindung wurden von anderen Autoren auch Serial Concatenated Convolutional Codes (SCCC) entsprechend folgender Grafik vorgeschlagen.
- Die Informationssequenz u liegt am äußeren Faltungscoder C1 an. Dessen Ausgangssequenz sei c.
- Nach dem Interleaver (Π) folgt der innere Faltungscoder C2. Die Codesequenz wird x genannt.
- Die resultierende Coderate ist R = R1 · R2. Bei Rate–1/2–Komponentencodes ist R = 1/4.
Die untere Grafik zeigt den SCCC–Decoder und verdeutlicht die Verarbeitung der L–Werte und den Austausch der extrinsischen Information zwischen den beiden Komponentencoder:
- Der innere Decoder (für den Code C2) erhält vom Kanal die intrinsische Information LK(x) und vom äußeren Decoder (nach Interleaving) die Apriori–Information LA(w) mit w = π(c). An den äußeren Decoder wird die extrinsische Information LE(w) abgegeben.
- Der äußere Decoder (für C1) verarbeitet die Apriori–Information LA(c), also die extrinsische Information LE(w) nach dem De–Interleaving. Er liefert die extrinsische Information LE(c).
- Nach hinreichend vielen Iterationen ergibt sich das das gewünschte Decodierergebnis in Form der Aposteriori–L–Werte LAPP(u) der Informationssequenz u.
Wichtig für seriell verkettete Faltungscodes ist, dass der innere Code rekursiv ist (also ein RSC–Code). Der äußere Code C1 kann auch nichtrekursiv sein. Zur Leistungsfähigkeit solcher Codes ist anzumerken:
- SCCCs sind bei großem EB/N0 besser als PCCCs ⇒ niedrigerer Error Floor. Die Aussage gilt schon für SCCC–Komponentencodes mit Gedächtnis m = 2 (nur vier Trelliszustände), während bei PCCC das Gedächtnis m = 3 bzw. m = 4 (acht bzw. sechzehn Trelliszustände) sein sollte.
- Im unteren Bereich (kleines EB/N0) ist dagegen der beste seriell verkettete Faltungscode (SCCC) um einige Zehntel Dezibel schlechter als der vergleichbare Turbocode gemäß Berrou (PCCC). Entsprechend größer ist auch der Abstand von der Shannongrenze.
Einige Anwendungsgebiete für Turbocodes
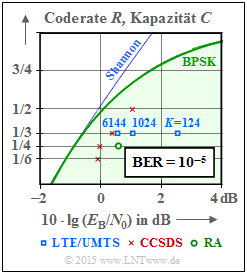
In fast allen neueren Kommunikationssystemen (nach 1993 standardisiert) werden Turbocodes eingesetzt. Die Grafik zeigt deren Leistungsfähigkeit beim AWGN–Kanal im Vergleich zur Shannonschen Kanalkapazität (blaue Kurve).
Der grün hinterlegte Bereich „BPSK” gibt die Shannongrenze für Nachrichtensystemee mit binärem Eingang an, mit der nach dem Kanalcodierungstheorem eine fehlerfreie Übertragung gerade noch möglich ist.
Anzumerken ist, dass hier für die eingezeichneten Kanalcodes von standardisierten Systemen die Fehlerrate 10–5 zugrunde liegt, während die informationstheoretischen Kapazitätskurven (Shannon, BPSK) für die Fehlerwahrscheinlichkeit 0 gelten.
- Die blauen Rechtecke markieren die Turbocodes für UMTS. Diese sind Rate–1/3–Codes mit Gedächtnis m = 3. Die Leistungsfähigkeit hängt stark von der Interleavergröße ab. Mit K = 6144 liegt dieser Code nur etwa 1 dB rechts von der Shannon–Grenze. LTE verwendet die gleichen Turbocodes. Geringfügige Unterschiede ergeben sich aufgrund des unterschiedlichen Interleavers.
- Die roten Kreuze markieren die Turbocodes nach CCSDS (Consultative Comittee for Space Data Systems), entwickelt für den Einsatz bei fernen Weltraummissionen. Diese Klasse geht von der einheitlichen Interleavergröße K = 6920 aus und stellt Codes der Rate 1/6, 1/4, 1/3 und 1/2 zur Verfügung. Die niedrigsten Coderaten erlauben einen Betrieb mit 10 · lg (EB/N0) ≈ 0 dB.
- Der grüne Kreis steht für einen sehr einfachen Repeat–Accumulate (RA) Code, einem seriell–verketteten Turbocode. Der äußere Decoder verwendet einen Wiederholungscode (englisch: Repetition Code), im gezeichneten Beispiel mit der Rate R = 1/3. Nach dem Interleaver folgt ein RSC–Code mit G(D) = 1/(1 + D) ⇒ Gedächtnis m = 1. Bei systematischer Ausführung ist die Gesamtcoderate R = 1/4 (zu jedem Informationsbit noch drei Paritybits). Aus der oberen Grafik erkennt man, dass dieser einfache RA–Code überraschend gut ist. Mit der Interleavergröße K = 300000 beträgt der Abstand von der Shannon–Grenze lediglich ca. 1.5 dB.
In der oberen Grafik nicht eingetragen sind die Turbocodes für den Standard DVB Return Channel Terrestrial (RCS) sowie für den WiMax–Standard (IEEE 802.16), die ähnliche Turbocodes benutzen.
Aufgaben
A4.8 Wiederholung zu den Faltungscodes
Zusatzaufgaben:4.8 Grundlegendes zum Interleaving
A4.9 Wiederholung zu den RSC-Codes
Quellenverzeichnis
- ↑ Liva, G.: Channels Codes for Iterative Decoding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2015.