Inhaltsverzeichnis
- 1 Statische und dynamische Wörterbuchtechniken
- 2 LZ77 – die Grundform der Lempel–Ziv–Algorithmen
- 3 Die Lempel–Ziv–Variante LZ78
- 4 Der Lempel–Ziv–Welch–Algorithmus
- 5 Lempel–Ziv–Codierung mit variabler Indexbitlänge
- 6 Decodierung des LZW–Algorithmus
- 7 Restredundanz als Maß für die Effizienz von Codierverfahren
- 8 Effizienz der Lempel–Ziv–Codierung
- 9 Quantitative Aussagen zur asymptotischen Optimalität
- 10 Aufgaben zum Kapitel
Statische und dynamische Wörterbuchtechniken
Viele Datenkomprimierungsverfahren verwenden Wörterbücher. Die Idee ist dabei die Folgende:
- Man konstruiere eine Liste der Zeichenmuster, die im Text vorkommen,
- und codiere diese Muster als Indizes der Liste.
Besonders effizient ist diese Vorgehensweise, wenn sich bestimmte Muster im Text häufig wiederholen und dies bei der Codierung auch berücksichtigt wird. Hierbei unterscheidet man:
- Verfahren mit statischem Wörterbuch,
- Verfahren mit dynamischem Wörterbuch.
$\text{(1) Verfahren mit statischem Wörterbuch}$
Ein statisches Wörterbuch ist nur für ganz spezielle Anwendungen sinnvoll, zum Beispiel für eine Datei der folgenden Form:
Beispielsweise ergibt sich mit den Zuordnungen
- $$"\boldsymbol{\rm 0}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 000000} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm 9}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001001} \hspace{0.05cm}, "\hspace{-0.03cm}\_\hspace{-0.03cm}\_\hspace{0.03cm}" \hspace{0.1cm}{\rm (Blank)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001010} \hspace{0.05cm},$$
- $$"\hspace{-0.01cm}.\hspace{-0.01cm}" \hspace{0.1cm}{\rm (Punkt)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001011} \hspace{0.05cm}, "\hspace{-0.01cm},\hspace{-0.01cm}" \hspace{0.1cm}{\rm (Komma)}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001011} \hspace{0.05cm}, " {\rm end\hspace{-0.1cm}-\hspace{-0.1cm}of\hspace{-0.1cm}-\hspace{-0.1cm}line}\hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 001101} \hspace{0.05cm},$$
- $$"\boldsymbol{\rm A}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 100000} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm E}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 100100} \hspace{0.05cm}, \hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm L}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101011} \hspace{0.05cm},\hspace{0.15cm}"\boldsymbol{\rm M}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101100} \hspace{0.05cm},$$
- $$"\boldsymbol{\rm O}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 101110} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm},\hspace{0.05cm} "\boldsymbol{\rm U}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 110100} \hspace{0.05cm}, "\boldsymbol{\rm Name\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010000} \hspace{0.05cm},\hspace{0.05cm}$$
- $$"\boldsymbol{\rm ,\_\hspace{-0.03cm}\_Vorname\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010001} \hspace{0.05cm},\hspace{0.05cm} "\boldsymbol{\rm ,\_\hspace{-0.03cm}\_Wohnort\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_}" \hspace{0.05cm} \mapsto \hspace{0.05cm} \boldsymbol{\rm 010010} \hspace{0.05cm},\hspace{0.15cm} ... \hspace{0.15cm}$$
für die mit jeweils sechs Bit pro Zeichen binär–quellencodierte erste Zeile des obigen Textes:
- $$\boldsymbol{010000} \hspace{0.15cm}\boldsymbol{100000} \hspace{0.15cm}\boldsymbol{100001} \hspace{0.15cm}\boldsymbol{100100} \hspace{0.15cm}\boldsymbol{101011} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{(\rm Name\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(A)\hspace{0.05cm}(B)\hspace{0.05cm}(E)\hspace{0.05cm}(L)}$$
- $$\boldsymbol{010001} \hspace{0.15cm}\boldsymbol{101011}\hspace{0.15cm} \boldsymbol{100100} \hspace{0.15cm}\boldsymbol{101110} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \boldsymbol{(,\hspace{-0.05cm}\_\hspace{-0.03cm}\_\rm Vorname\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(L)\hspace{0.05cm}(E)\hspace{0.05cm}(O)}$$
- $$\boldsymbol{010010} \hspace{0.15cm}\boldsymbol{110100} \hspace{0.15cm}\boldsymbol{101011} \hspace{0.15cm}\boldsymbol{101100} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \boldsymbol{(,\hspace{-0.05cm}\_\hspace{-0.03cm}\_\rm Wohnort\hspace{-0.1cm}:\hspace{-0.05cm}\_\hspace{-0.03cm}\_) \hspace{0.05cm}(U)\hspace{0.05cm}(L)\hspace{0.05cm}(M)} \hspace{0.05cm} $$
- $$\boldsymbol{001101} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ({\rm end\hspace{-0.1cm}-\hspace{-0.1cm}of\hspace{-0.1cm}-\hspace{-0.1cm}line}) \hspace{0.05cm}$$
$\text{Fazit:}$ Bei dieser spezifischen Anwendung lässt sich die erste Zeile mit $14 · 6 = 84$ Bit darstellen.
- Dagegen würde man bei herkömmlicher Binärcodierung $39 · 7 = 273$ Bit benötigen, weil:
Aufgrund der Kleinbuchstaben im Text reichen hier sechs Bit pro Zeichen nicht aus. - Für den gesamten Text ergeben sich $103 · 6 = 618$ Bit gegenüber $196 · 7 = 1372$ Bit.
- Allerdings muss die Codetabelle auch dem Empfänger bekannt sein.
$\text{(2) Verfahren mit dynamischem Wörterbuch}$
Alle relevanten Komprimierungsverfahren arbeiten allerdings nicht mit statischem Wörterbuch, sondern mit „dynamischen Wörterbüchern”, die erst während der Codierung sukzessive entstehen:
- Solche Verfahren sind flexibel einsetzbar und müssen nicht an die Anwendung adaptiert werden. Man spricht von universellen Quellencodierverfahren.
- Dann genügt ein einziger Durchlauf, während bei statischem Wörterbuch die Datei vor dem Codiervorgang erst analysiert werden muss.
- An der Sinke wird das dynamische Wörterbuch in gleicher Weise generiert wie bei der Quelle. Damit entfällt die Übertragung des Wörterbuchs.
$\text{Beispiel 1:}$ Die Grafik zeigt einen kleinen Ausschnitt von $80$ Byte einer BMP–Datei in Hexadezimaldarstellung. Es handelt sich um die unkomprimierte Darstellung eines natürlichen Bildes.
- Man erkennt, dass in diesem kleinen Ausschnitt einer Landschaftsaufnahme die Bytes $\rm FF$, $\rm 55$ und $\rm 47$ sehr häufig auftreten.
- Eine Datenkomprimierung ist deshalb erfolgversprechend.
- Da aber an anderen Stellen der $\text{4 MByte}$–Datei oder bei anderem Bildinhalt andere Bytekombinationen dominieren, wäre hier die Verwendung eines statischen Wörterbuchs nicht zielführend.
$\text{Beispiel 2:}$ Bei einer künstlich erzeugten Grafik – zum Beispiel einem Formular – könnte man dagegen durchaus mit statischem Wörterbuch arbeiten.
Wir betrachten hier ein S/W–Bild mit $27 × 27$ Pixeln, wobei die Zuordnung „Schwarz” ⇒ 0 und „Weiß” ⇒ 1 vereinbart wurde.
- Oben (schwarze Markierung) wird jede Zeile durch $27$ Nullen beschrieben.
- In der Mitte (blaue Markierung) wechseln sich stets drei Nullen und drei Einsen ab.
- Unten (rote Markierung) werden pro Zeile $25$ Einsen durch zwei Nullen begrenzt.
LZ77 – die Grundform der Lempel–Ziv–Algorithmen
Die wichtigsten Verfahren zur Datenkomprimierung mit dynamischem Wörterbuch gehen auf Abraham Lempel und Jacob Ziv zurück. Die gesamte Lempel–Ziv–Familie (im Folgenden verwenden wir hierfür kurz: $\rm LZ$–Verfahren) kann wie folgt charakterisiert werden:
- Lempel–Ziv–Verfahren nutzen die Tatsache, dass in einem Text oft ganze Wörter – oder zumindest Teile davon – mehrfach vorkommen. Man sammelt alle Wortfragmente, die man auch als „Phrasen” bezeichnet, in einem ausreichend großen Wörterbuch.
- Im Gegensatz zur ein paar Jahre vorher (von Shannon und Huffman) entwickelten Entropiecodierung ist hier nicht die Häufigkeit einzelner Zeichen oder Zeichenfolgen die Grundlage der Komprimierung, so dass die LZ–Verfahren auch ohne Kenntnis der Quellenstatistik angewendet werden können.
- Eine LZ–Komprimierung kommt dementsprechend mit einem einzigen Durchgang aus und auch der Quellensymbolumfang $M$ und die Symbolmenge $\{q_μ\}$ mit $μ = 1$, ... , $M$ muss nicht bekannt sein. Man spricht von universeller Quellencodierung (englisch: "Universal Source Coding").
Wir betrachten zunächst den Lempel–Ziv–Algorithmus in seiner ursprünglichen Form aus dem Jahre 1977, bekannt unter der Bezeichnung $\rm LZ77$:
- Dieser arbeitet mit einem Fenster, das sukzessive über den Text verschoben wird. Man spricht auch von einem „Sliding Window”.
- Die Fenstergröße $G$ ist dabei ein wichtiger Parameter, der das Komprimierungsergebnis entscheidend beeinflusst.
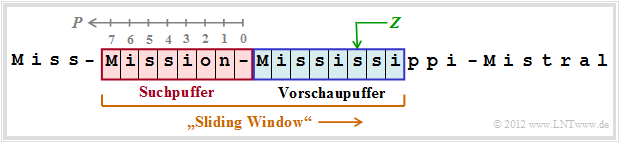
Die Grafik zeigt eine beispielhafte Belegung des Sliding Windows. Dieses ist unterteilt in
- den Vorschaupuffer $($blaue Hinterlegung), und
- den Suchpuffer $($rote Hinterlegung, mit den Positionen
$P = 0$, ... , $7$ ⇒ Fenstergröße $G = 8)$.
Der bearbeitete Text umfasst die vier Worte Miss, Mission, Mississippi und Mistral, jeweils getrennt durch einen Bindestrich. Zum betrachteten Zeitpunkt steht im Vorschaupuffer Mississi.
- Gesucht wird nun im Suchpuffer die beste Übereinstimmung ⇒ die Zeichenfolge mit der maximalen Übereinstimmungslänge $L$. Diese ergibt sich für die Position $P = 7$ und die Länge $L = 5$ zu Missi.
- Dieser Schritt wird dann durch das Triple $(7, 5, $ s$)$ ausgedrückt ⇒ allgemein $(P, \ L, \ Z)$, wobei $Z =$ s dasjenige Zeichen angibt, das nicht mehr mit der gefundenen Zeichenfolge im Suchpuffer übereinstimmt.
- Anschließend wird das Fenster um $L + 1 = 6$ Zeichen nach rechts verschoben. Im Vorschaupuffer steht nun sippi–Mi, im Suchpuffer n–Missis und die Codierung ergibt das Triple $(2, 2,$ p$)$.
Im folgenden Beispiel wird der LZ77–Codier–Algorithmen genauer beschrieben. Die Decodierung läuft in vergleichbarer Weise ab.
$\text{Beispiel 3:}$ Wir betrachten die LZ77–Codierung des Strings ABABCBCBAABCABe entsprechend der folgenden Grafik. Die Eingangsfolge hat die Länge $N = 15$.
Weiter wird vorausgesetzt:
- Für die Zeichen gelte $Z ∈ \{$ A, B, C, e $\}$, wobei e dem "end–of–file" (Ende des Eingabe–Strings) entspricht,
- Die Größe von Vorschau– und Suchpuffer sind jeweils $G = 4$ ⇒ Position $P ∈ \{0,\ 1,\ 2,\ 3\}$.
Darstellung des Codiervorgangs:
Schritt 1 und 2: Es werden die Zeichen A und B durch die Triple $(0, 0, $ A$)$ und $(0, 0, $ B$)$ codiert, da diese im Suchpuffer noch nicht abgelegt sind. Dann Verschiebung des Sliding Window jeweils um 1.
Schritt 3: AB wird über den Suchpuffer maskiert und gleichzeitig das noch unbekannte Zeichen C angehängt. Danach wird das Sliding Window um drei Positionen nach rechts verschoben.
Schritt 4: Hier wird gezeigt, dass der Suchstring BCB auch im Vorschaupuffer enden darf. Jetzt kann das Fenster um vier Positionen verschoben werden.
Schritt 5: Es wird im Suchpuffer lediglich A gefunden und B abgehängt. Bei größerem Suchpuffer könnten dagegen ABC gemeinsam maskiert werden. Dazu müsste $G ≥ 7$ sein.
Schritt 6: Ebenso muss das Zeichen C aufgrund des zu kleinen Puffers separat codiert werden. Da aber CA vorher noch nicht aufgetreten ist, würde hier $G = 7$ die Komprimierung nicht verbessern.
Schritt 7: Mit der Berücksichtigung des end–of–file (e) gemeinsam mit AB aus dem Suchpuffer ist der Codiervorgang abgeschlossen.
Vor der Übertragung müssen natürlich die angegebenen Triple noch binär codiert werden. Dabei benötigt man im vorliegenden Beispiel für
- die Position $P ∈ \{0,\ 1,\ 2,\ 3\}$ zwei Bit (gelbe Hinterlegung in obiger Tabelle),
- die Kopierlänge $L$ drei Bit (grün hinterlegt), so dass man auch $L = 7$ noch darstellen könnte,
- alle Zeichen jeweils zwei Bit (weiß hinterlegt), zum Beispiel A → 00, B → 01, C → 10, e („end–of–file”) → 11.
Damit hat die $\rm LZ77$–Ausgangsfolge eine Länge von $7 · 7 = 49$ Bit, während die Eingangsfolge nur $15 · 2 = 30$ Bit benötigt hat.
$\text{Fazit:}$ Eine Lempel–Ziv–Komprimierung macht nur bei großen Dateien Sinn !
Die Lempel–Ziv–Variante LZ78
Der LZ77–Algorithmus erzeugt dann eine sehr ineffiziente Ausgabe, wenn sich häufigere Zeichenfolgen erst mit größerem Abstand wiederholen. Solche Wiederholungen können aufgrund der begrenzten Puffergröße $G$ des Sliding Windows oft nicht erkannt werden.
Lempel und Ziv haben dieses Manko bereits ein Jahr nach der Veröffentlichung der ersten Version LZ77 korrigiert:
- Der Algorithmus LZ78 verwendet zur Komprimierung anstelle des lokalen Wörterbuchs (Suchpuffer) ein globales Wörterbuch.
- Bei entsprechender Wörterbuchgröße lassen sich somit auch solche Phrasen, die schon längere Zeit vorher aufgetreten sind, effizient komprimieren.
$\text{Beispiel 4:}$ Zur Erklärung des LZ78–Algorithmus betrachten wir die gleiche Folge ABABCBCBAABCABe wie für das LZ77–$\text{Beispiel 3}$.
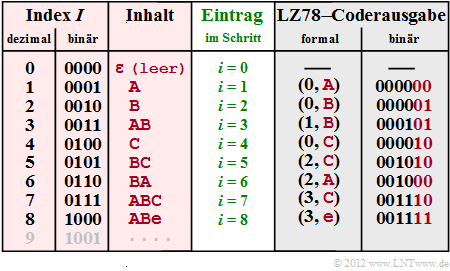
Die Grafik zeigt (mit roter Hinterlegung) das Wörterbuch mit Index $I $ (in Dezimal– und Binärdarstellung, Spalte 1 und 2) und dem entsprechenden Inhalt (Spalte 3), der zum Codierschritt $i $ eingetragen wird (Spalte 4).
- Bei LZ78 gilt sowohl für die Codierung als auch für die Decodierung stets $i = I$.
- In Spalte 5 findet man die formalisierte Coderausgabe $($Index $I$, neues Zeichen $Z)$.
- In Spalte 6 ist die dazugehörige Binärcodierung angegeben mit vier Bit für den Index und der gleichen Zeichenzuordnung A → 00, B → 01, C → 10, e („end–of–file”) → 11 wie im $\text{Beispiel 3}$.
- Zu Beginn (Schritt $\underline{i = 0}$) ist das Wörterbuch $\rm (WB)$ leer bis auf den Eintrag ε $($leeres Zeichen, nicht zu verwechseln mit dem Leerzeichen, das aber hier nicht verwendet wird$)$ mit Index $I = 0$.
- Im Schritt $\underline{i = 1}$ findet man im Wörterbuch noch keinen verwertbaren Eintrag, und es wird (0, A) ausgegeben (A folgt auf ε). Im Wörterbuch erfolgt der Eintrag A in Zeile $I = 1$ (abgekürzt 1: A).
- Damit vergleichbar ist die Vorgehensweise im zweiten Schritt ($\underline{i = 2}$). Ausgegeben wird hier (0, B) und ins Wörterbuch wird 2: B eingetragen.
- Da bei Schritt $\underline{i = 3}$ bereits der Eintrag 1: A gefunden wird, können hier die Zeichen AB gemeinsam durch (1, B) codiert werden und es wird der neue Wörterbucheintrag 3: AB vorgenommen.
- Nach Codierung und Eintrag des neuen Zeichens C in Schritt $\underline{i = 4}$ wird im Schritt $\underline{i = 5}$ das Zeichenpaar BC gemeinsam codiert ⇒ (2, C) und in das Wörterbuch 5: BC eingetragen.
- In Schritt $\underline{i = 6}$ werden mit 6: BA ebenfalls zwei Zeichen gemeinsam behandelt und in den beiden letzten Schritten jeweils drei, nämlich 7: ABC und 8: ABe.
- Die Ausgabe (3, C) in Schritt $\underline{i = 7}$ steht für „WB(3) + C” = ABC und die Ausgabe (3, e) in Schritt $\underline{i = 8}$ für ABe.
In diesem $\text{Beispiel 4}$ besteht somit die $\rm LZ78$–Codesymbolfolge aus $8 · 6 = 48$ Bit. Das Ergebnis ist vergleichbar mit dem LZ77–$\text{Beispiel 3}$ $(49$ Bit$)$.
$\text{Fazit:}$ Auf Details und Verbesserungen von $\rm LZ78$ wird hier verzichtet. Hier verweisen wir auf den LZW–Algorithmus, der auf den nächsten Seiten beschrieben wird. Soviel nur vorneweg:
- Der Index $I$ wird hier einheitlich mit vier Bit dargestellt, wodurch das Wörterbuch auf $16$ Einträge beschränkt ist. Durch eine variable Bitanzahl für den Index kann man diese Einschränkung umgehen. Gleichzeitig erhält man so einen besseren Komprimierungsfaktor.
- Das Wörterbuch muss bei allen LZ–Varianten nicht übertragen werden, sondern wird beim Decoder in genau gleicher Weise erzeugt wie auf der Coderseite. Die Decodierung erfolgt bei LZ78 – nicht aber bei LZW – ebenfalls in analoger Weise wie die Codierung.
- Alle LZ–Verfahren sind asymptotisch optimal, das heißt, dass bei unendlich langen Folgen die mittlere Codewortlänge $L_{\rm M}$ pro Quellensymbol gleich der Quellenentropie $H$ ist.
- Bei kurzen Folgen ist die Abweichung allerdings beträchtlich. Mehr dazu am Kapitelende.
Der Lempel–Ziv–Welch–Algorithmus
Die heute gebräuchlichste Variante der Lempel–Ziv–Komprimierung wurde von Terry Welch entworfen und 1983 veröffentlicht.
- Wir bezeichnen diese im Folgenden als den Lempel–Ziv–Welch–Algorithmus, abgekürzt mit $\rm LZW$.
- Ebenso wie LZ78 leichte Vorteile gegenüber LZ77 aufweist (wie zu erwarten – warum sonst hätte der Algorithmus modifiziert werden sollen?),
hat LZW gegenüber LZ78 auch mehr Vorteile als Nachteile.
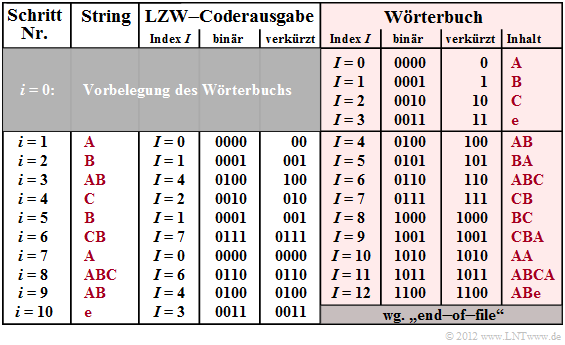
Die Grafik zeigt die Coderausgabe für unsere beispielhafte Eingangsfolge ABABCBCBAABCABe. Rechts dargestellt ist das Wörterbuch (rot hinterlegt), das bei der LZW–Codierung sukzessive entsteht. Die Unterschiede gegenüber LZ78 erkennt man im Vergleich zur Grafik auf der letzten Seite, nämlich:
- Bei LZW sind im Wörterbuch schon zu Beginn $(i = 0)$ alle im Text vorkommenden Zeichen eingetragen und einer Binärfolge zugeordnet, im Beispiel mit den Indizes $I = 0$, ... , $I = 3$.
- Das bedeutet aber auch, dass bei LZW doch gewisse Kenntnisse über die Nachrichtenquelle vorhanden sein müssen, während LZ78 eine „echte universelle Codierung” darstellt.
- Bei LZW wird zu jedem Codierschritt $i$ nur der Wörterbuchindex $I$ übertragen, während bei LZ78 die Kombination $(I$, $Z)$ ausgegeben wird; $Z$ bezeichnet dabei das aktuell neue Zeichen.
- Aufgrund des Fehlens von $Z$ in der Coderausgabe ist die LZW–Decodierung komplizierter als bei LZ78, wie auf der Seite Decodierung des LZW–Algorithmus beschrieben wird.
$\text{Beispiel 5:}$ Für diese beispielhafte LZW–Codierung wird wie bei „LZ77” und „LZ78” wieder die Eingangsfolge ABABCBCBAABCABe vorausgesetzt. Die folgende Beschreibung bezieht sich also auf die obige Grafik.
Schritt i = 0 (Vorbelegung): Die erlaubten Zeichen A, B, C und e („end–of–file”) werden in das Wörterbuch eingetragen und den Indizes $I = 0$, ... , $I = 3$ zugeordnet.
Schritt i = 1: Das Zeichen A wird durch den Dezimalindex $I = 0$ codiert und dessen Binärdarstellung 0000 übertragen. Anschließend wird ins Wörterbuch die Kombination aus dem aktuellen Zeichen A und dem nachfolgenden Zeichen B der Eingangsfolge unter dem Index $I = 4$ abgelegt.
Schritt i = 2: Darstellung von B durch Index $I = 1$ bzw. 0001 (binär) sowie Wörterbucheintrag von BA unter dem Index $I = 5$.
Schritt i = 3: Aufgrund des Eintrags AB zum Zeitpunkt $i = 1$ ist der zu übertragende Index $I = 4$ (binär: 0100). Neuer Eintrag ins Wörterbuch: ABC unter $I = 6$.
Schritt i = 8: Hier werden die Zeichen ABC gemeinsam durch den Index $I = 6$ (binär: 0110) dargestellt und der Eintrag für ABCA vorgenommen.
Mit der Codierung von e (EOF–Marke) ist der Codiervorgang nach zehn Schritten beendet. Bei LZ78 wurden nur acht Schritte benötigt. Es ist aber zu berücksichtigen:
- Der LZW–Algorithmus benötigt für die Darstellung dieser fünfzehn Eingangssymbole nur $10 · 4 = 40$ Bit gegenüber den $8 · 6 = 48$ Bit bei LZ78. Vorausgesetzt sind für diese einfache Rechnung jeweils vier Bit zur Indexdarstellung.
- Sowohl bei LZW als auch bei LZ78 kommt man mit weniger Bit aus $($nämlich mit $34$ bzw. $42)$, wenn man berücksichtigt, dass zum Schritt $i = 1$ der Index nur mit zwei Bit codiert werden muss $(I ≤ 3)$ und für $i = 2$ bis $i = 5$ drei Bit ausreichen $(I ≤ 7)$.
Auf den nächsten Seiten wird auf die variable Bitanzahl zur Indexdarstellung sowie auf die Decodierung von LZ78– und LZW–codierten Binärfolgen im Detail eingegangen.
Lempel–Ziv–Codierung mit variabler Indexbitlänge
Aus Gründen einer möglichst kompakten Darstellung betrachten wir nun nur noch Binärquellen mit dem Wertevorrat $\{$A, B$\}$. Das Abschlusszeichen end–of–file bleibt ebenfalls unberücksichtigt.
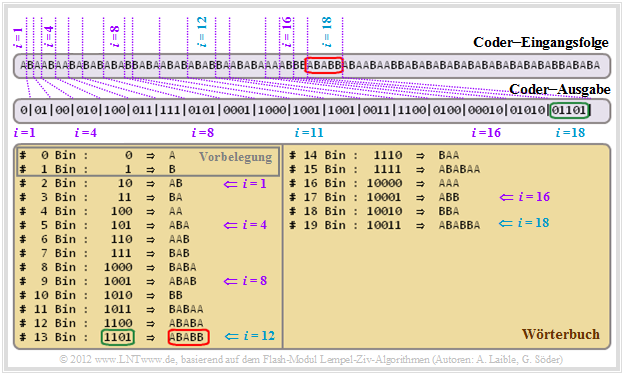
Wir demonstrieren die LZW–Codierung anhand eines Bildschirmabzugs unseres interaktiven SWF–Moduls Lempel–Ziv–Welch–Algorithmen.
- Beim ersten Codierschritt $(i = 1)$ wird A ⇒ 0 codiert. Danach erfolgt im Wörterbuch der Eintrag mit dem Index $I = 2$ und dem Inhalt AB.
- Da es bei Schritt $i = 1$ im Wörterbuch mit A und B nur zwei Einträge gibt, genügt ein Bit. Dagegen werden bei Schritt $i = 2$ und $i = 3$ für B ⇒ 01 bzw. A ⇒ 00 jeweils zwei Bit benötigt.
- Ab $i = 4$ erfolgt die Indexdarstellung mit drei Bit, ab $i = 8$ mit vier Bit und ab $i = 16$ mit fünf Bit. Hieraus lässt sich ein einfacher Algorithmus für die jeweilige Index–Bitanzahl $L(i)$ ableiten.
- Betrachten wir abschließend den Codierschritt $i = 18$. Hier wird die rot markierte Sequenz ABABB, die zum Zeitpunkt $i = 11$ in das Wörterbuch eingetragen wurde $($Index $I = 13$ ⇒ 1101$)$ bearbeitet. Die Coder–Ausgabe lautet wegen $i ≥ 16$ aber nun 01101 (grüne Markierung bei der Coder–Ausgabe).
Die Aussagen gelten auch für LZ78.
Das heißt: Beim LZ78 ergibt sich durch eine variable Indexbitlänge die gleiche Verbesserung wie beim LZW.
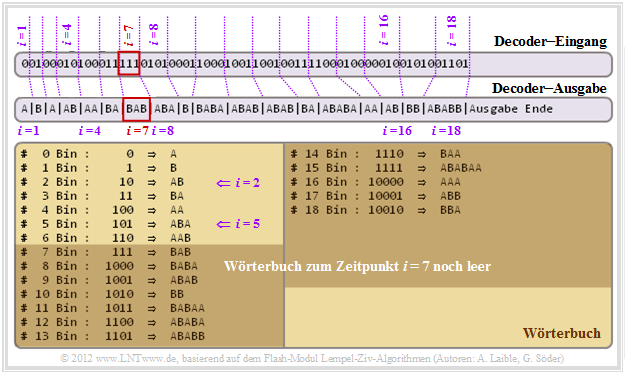
Decodierung des LZW–Algorithmus
Am Decoder liegt nun die auf der letzten Seite ermittelte Coder–Ausgabe als Eingangsfolge an. Die Grafik zeigt, dass es auch bei variabler Indexbitlänge möglich ist, diese Folge eindeutig zu decodieren. Bitte beachten Sie:
- Dem Decoder ist bekannt, dass im ersten Codierschritt $(i = 1)$ der Index $I $ mit nur einem Bit codiert wurde, in den Schritten $i = 2$ und $i = 3$ mit zwei Bit, ab $i = 4$ mit drei Bit, ab $i = 8$ mit vier Bit, usw.
- Beim Decoder wird das gleiche Wörterbuch generiert wie beim Coder, doch erfolgen hier die Wörterbucheinträge einen Zeitschritt später.
- Zum Schritt $\underline{i = 1}$ wird also das anliegende Symbol 0 als A decodiert. Ebenso ergibt sich zum Schritt $\underline{i = 2}$ aus der Vorbelegung des Wörterbuches und der hierfür vereinbarten Zwei–Bit–Darstellung: 01 ⇒ B.
- Der Eintrag der Zeile $\underline{I = 2}$ $($Inhalt: AB$)$ des Wörterbuchs erfolgt also erst zum Schritt $\underline{i = 2}$. Beim Codiervorgang konnte dies bereits am Ende von Schritt $i = 1$ geschehen.
- Betrachten wir nun die Decodierung für $\underline{i = 4}$. Der Index $\underline{I = 2}$ liefert das Ergebnis 010 ⇒ AB und im nächsten Schritt $(\underline{i = 5})$ wird die Wörterbuchzeile $\underline{I = 5}$ mit ABA belegt.
- Diese Zeitverschiebung hinsichtlich der Wörterbuch–Einträge kann zu Decodierproblemen führen. So gibt es zum Schritt $\underline{i = 7}$ noch keinen Wörterbuch–Eintrag mit Index $\underline{I= 7}$.
- Was ist in einem solchen Fall $(\underline{I = i})$ zu tun? Man nimmt das Ergebnis des vorherigen Decodierschrittes $($hier: BA für $\underline{i = 6})$ und fügt das erste Zeichen dieser Sequenz am Ende noch einmal an. Decodierergebnis für $\underline{i = 7}$ zu 111 ⇒ BAB.
Natürlich ist es unbefriedigend, nur ein Rezept anzugeben. In Aufgabe 2.4Z sollen Sie die zugehörige Begründung liefern. Siehe Musterlösung. – Bei der LZ78–Decodierung tritt das hier geschilderte Problem nicht auf, da nicht nur der Index $I $, sondern auch das aktuelle Zeichen $Z$ im Codierergebnis enthalten ist und übertragen wird.
Restredundanz als Maß für die Effizienz von Codierverfahren
Für den Rest dieses Kapitels gehen wir von folgenden Voraussetzungen aus:
- Der Symbolumfang der Quelle $($oder im übertragungstechnischen Sinne: die Stufenzahl) sei $M$, wobei $M$ eine Zweierpotenz darstellt ⇒ $M = 2, \ 4, \ 8, \ 16$, ....
- Die Quellenentropie sei $H$. Gibt es keine statistischen Bindungen zwischen den Symbolen und sind diese zudem gleichwahrscheinlich, so gilt $H = H_0$, wobei $H_0 = \log_2 \ M$ den Entscheidungsgehalt angibt. Andernfalls gilt $H < H_0$.
- Eine Symbolfolge der Länge $N$ wird quellencodiert und liefert eine binäre Codefolge der Länge $L$. Über die Art der Quellencodierung treffen wir vorerst keine Aussage.
Nach dem Quellencodierungstheorem muss dann die mittlere Codewortlänge $L_{\rm M}$ größer oder gleich der Quellenentropie $H$ (in bit/Quellensymbol) sein. Das bedeutet
- für die Gesamtlänge der quellencodierten Binärfolge:
- $$L \ge N \cdot H \hspace{0.05cm},$$
- für die relative Redundanz der Codefolge, im Folgenden kurz Restredundanz genannt:
- $$r = \frac{L - N \cdot H}{L} \hspace{0.05cm}.$$
$\text{Beispiel 6:}$ Gäbe es für eine redundanzfreie binäre Quellensymbolfolge $(M = 2,\ p_{\rm A} = p_{\rm B} = 0.5$, ohne statistische Bindungen$)$ der Länge $N = 10000$ eine „perfekte Quellencodierung”, so hätte auch die Codefolge die Länge $L = 10000$.
Konsequenz: Ist bei einem Code das Ergebnis $L = N$ nie möglich, so bezeichnet man diesen Code als „nicht–perfekt”.
- Für diese redundanzfreie Nachrichtenquelle ist Lempel–Ziv nicht geeignet. Es wird stets $L > N$ gelten. Man kann es auch ganz lapidar so ausdrücken: Die perfekte Quellencodierung ist hier „gar keine Codierung”.
- Eine redundante Binärquelle mit $p_{\rm A} = 0.89$, $p_{\rm B} = 0.11$ ⇒ $H = 0.5$ könnte man mit einer perfekten Quellencodierung durch $L = 5000$ Bit darstellen, ohne dass wir hier sagen können, wie diese perfekte Quellencodierung aussieht.
- Bei einer Quaternärquelle ist $H > 1 \ \rm (bit/Quellensymbol)$ möglich, so dass auch bei perfekter Codierung stets $L > N$ sein wird. Ist die Quelle redundanzfrei (keine Bindungen, alle $M$ Symbole gleichwahrscheinlich), so hat sie die Entropie $H= 2 \ \rm (bit/Quellensymbol)$.
Bei allen diesen Beispielen für perfekte Quellencodierung wäre die relative Redundanz der Codefolge (also die Restredundanz) $r = 0$. Das heißt: Die Nullen und Einsen sind gleichwahrscheinlich und es bestehen keine statistischen Bindungen zwischen den einzelnen Binärsymbolen.
Das Problem ist: Bei endlicher Folgenlänge $N$ gibt es keine perfekte Quellencodierung !
Effizienz der Lempel–Ziv–Codierung
Von den Lempel–Ziv–Algorithmen weiß man (und kann diese Aussage sogar beweisen), dass sie asymptotisch optimal sind. Das bedeutet, dass die relative Redundanz der Codesymbolfolge (hier als Funktion der Quellensymbolfolgenlänge $N$ geschrieben)
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}$$
für große $N$ den Grenzwert „Null” liefert:
- $$\lim_{N \rightarrow \infty}r(N) = 0 \hspace{0.05cm}.$$
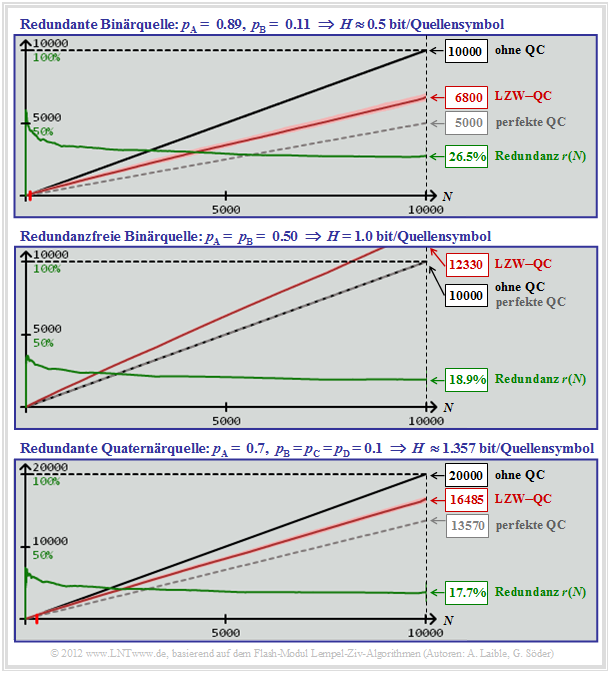
Was aber sagt die Eigenschaft „asymptotisch optimal” für praxisrelevante Folgenlängen aus? Nicht allzu viel, wie der nachfolgende Bildschirmabzug unseres Simulationstools Lempel–Ziv–Algorithmen zeigt. Alle Kurven gelten exakt nur für den LZW–Algorithmus. Die Ergebnisse für LZ77 und LZ78 sind aber nur geringfügig schlechter.
Die drei Grafiken zeigen für verschiedene Nachrichtenquellen die Abhängigkeit folgender Größen von der Quellensymbolfolgenlänge $N$:
- die erforderliche Bitanzahl $N · \log_2 M$ ohne Quellencodierung (schwarze Kurven),
- die erforderliche Bitanzahl $H$ · $N$ bei perfekter Quellencodierung (grau–gestrichelt),
- die erforderliche Bitanzahl $L(N)$ bei LZW–Codierung (rote Kurven nach Mittelung),
- die relative Redundanz ⇒ Restredundanz $r(N)$ bei LZW–Codierung (grüne Kurven).
$\underline{\text{Redundante Binärquelle (obere Grafik)} }$
- $$M = 2, \hspace{0.1cm}p_{\rm A} = 0.89,\hspace{0.1cm} p_{\rm B} = 0.11$$
- $$\Rightarrow \hspace{0.15cm} H = 0.5 \ \rm bit/Quellensymbol\text{:}$$
- Die schwarze und die graue Kurve sind echte Gerade (nicht nur bei diesem Parametersatz).
- Die rote Kurve $L(N)$ ist leicht gekrümmt (mit bloßem Auge schwer zu erkennen).
- Wegen dieser Krümmung von $L(N)$ fällt die Restredundanz (grüne Kurve) leicht ab.
- $$r(N) = 1 - 0.5 · N/L(N).$$
- Abzulesen sind die Zahlenwerte
- $$L(N = 10000) = 6800,\hspace{0.5cm} r(N = 10000) = 26.5\%.$$
$\underline{\text{Redundanzfreie Binärquelle (mittlere Grafik)} }$
- $$M = 2,\hspace{0.1cm} p_{\rm A} = p_{\rm B} = 0.5$$
- $$\Rightarrow \hspace{0.15cm} H = 1 \ \rm bit/Quellensymbol\text{:}$$
- Hier fallen die graue und die schwarze Gerade zusammen und die leicht gekrümmte rote Kurve liegt erwartungsgemäß darüber.
- Obwohl hier die LZW–Codierung eine Verschlechterung bringt – erkennbar aus der Angabe $L(N = 10000) = 12330$, ist die relative Redundanz kleiner als bei der oberen Grafik:
- $$r(N = 10000) = 18.9\%.$$
$\underline{\text{Redundante Quaternärquelle (untere Grafik)} }$
- $$M = 4,\hspace{0.1cm}p_{\rm A} = 0.7,\hspace{0.1cm} p_{\rm B} = p_{\rm C} = p_{\rm D} = 0.1$$
- $$ \Rightarrow \hspace{0.15cm} H \approx 1.357 \ \rm bit/Quellensymbol\text{:}$$
- Ohne Quellencodierung wären für $N = 10000$ Quaternärsymbole $20000$ Binärsymbole (Bit) erforderlich (schwarze Kurve).
- Bei perfekter Quellencodierung ergäben sich $N \cdot H= 13570$ Bit (graue Kurve).
- Mit der (nicht perfekten) LZW–Codierung benötigt man $L(N = 10000) ≈ 16485$ Bit (rote Kurve).
- Die relative Redundanz beträgt hier $r(N = 10000) ≈17.7\%$ (grüne Kurve).
Quantitative Aussagen zur asymptotischen Optimalität
Die Ergebnisse der letzten Seite haben gezeigt, dass die relative Restredundanz $r(N = 10000)$ deutlich größer ist als der theoretisch versprochene Wert $r(N \to \infty) = 0$.
Dieses praxisrelevante Ergebnis soll nun am Beispiel der redundanten Binärquelle mit $H = 0.5 \ \rm bit/Quellensymbol$ entsprechend der mittleren Grafik auf der letzten Seite präzisiert werden, wobei wir aber nun für die Quellensymbolfolgenlänge Werte zwischen $N=10^3$ und $N=10^{12}$ betrachten.
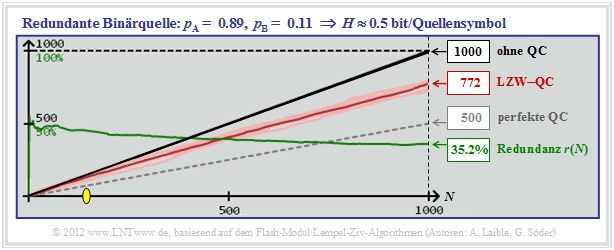
$\text{Beispiel 7:}$ Die Grafik zeigt Simulationen mit $N = 1000$ Binärsymbolen.
- Nach Mittelung über zehn Versuchsreihen ergibt sich $r(N = 1000) ≈35.2\%$.
- Unterhalb des gelben Punktes $($im Beispiel bei $N ≈ 150)$ bringt der LZW–Algorithmus sogar eine Verschlechterung.
- In diesem Bereich gilt nämlich $L > N$, das heißt:
Die rote Kurve liegt geringfügig oberhalb der schwarzen.
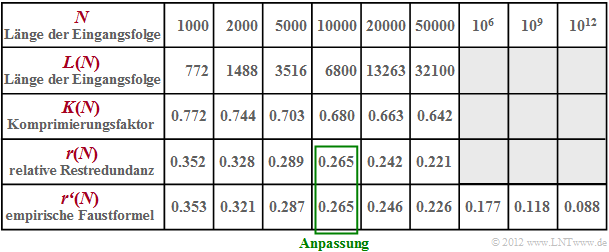
In der unteren Tabelle sind die Ergebnisse für diese redundante Binärquelle $(H = 0.5)$ zusammengefasst:
- Der Komprimierungsfaktor $K(N)= L(N)/N$ nimmt mit steigendem $N$ nur sehr langsam ab (Zeile 3).
- In Zeile 4 ist die Restredundanz $r(N)$ für verschiedene Längen zwischen $N =1000$ und $N =50000$ angegeben.
- Entsprechend einschlägiger Literaturangaben nimmt diese Restredundanz proportional zu $\big[\hspace{0.05cm}\lg(N)\hspace{0.05cm}\big]^{-1}$ ab.
- In Zeile 5 sind die Ergebnisse einer empirischen Formel eingetragen $($Anpassung für $N = 10000)$:
- $$r\hspace{0.05cm}'(N) = \frac{A}{ {\rm lg}\hspace{0.1cm}(N)}\hspace{0.5cm}{\rm mit}$$
- $$ A = {r(N = 10000)} \cdot { {\rm lg}\hspace{0.1cm}10000} = 0.265 \cdot 4 = 1.06 \hspace{0.05cm}.$$
- Man erkennt die gute Übereinstimmung zwischen unseren Simulationsergebnissen $r(N)$ und der Faustformel $r\hspace{0.05cm}′(N)$.
- Man erkennt aber auch, dass die Restredundanz des LZW–Algorithmus für $N = 10^{12}$ noch immer $8.8\%$ beträgt.
- Bei anderen Quellen erhält man mit anderen $A$–Werten ähnliche Ergebnisse. Der prinzipielle Verlauf bleibt gleich. Siehe auch Aufgabe 2.5 und Aufgabe 2.5Z.
Aufgaben zum Kapitel
Aufgabe 2.3: Zur LZ78-Komprimierung
Aufgabe 2.3Z: Zur LZ77-Codierung
Aufgabe 2.4: Zum LZW-Algorithmus
Aufgabe 2.4Z: Nochmals LZW-Codierung und -Decodierung
Aufgabe 2.5: Restredundanz bei LZW-Codierung
Aufgabe 2.5Z: Komprimierungsfaktor vs. Restredundanz