Phasenmodulation (PM)

1. Modulationsverfahren
2. Winkelmodulation und WM–Demodulation
3. Phasenmodulation (PM)

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Das dritte Kapitel beschreibt die Winkelmodulation (WM) – dieser Name steht als Oberbegriff für Phasenmodulation (PM) und Fequenzmodulation (FM) – sowie die zugehörigen Demodulatoren. Im Einzelnen werden behandelt:

• die Gemeinsamkeiten und Unterschiede zwischen Phasen– und Frequenzmodulation,
• die Signalverläufe und Spektralfunktion winkelmodulierter Signale und Einfluss einer Bandbegrenzung,
• das gegenüber der AM günstigere Signal–zu–Rausch–Leistungsverhältnis der FM.

Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Analoge Modulationsverfahren” des Praktikums „Simulation Digitaler Übertragungssysteme ”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

• dem Windows-Programm AMV  ⇒  Link verweist auf die ZIP-Version des Programms; und
• der zugehörigen Praktikumsanleitung  ⇒  Link verweist auf die PDF-Version.

Der erste Abschnitt „Phasenmodulation” ist wie folgt gegliedert:

Gemeinsamkeiten zwischen Phasen– und Frequenzmodulation

Schon im Kapitel Allgemeines Modell der Modulation wurde darauf hingewiesen, dass es zwischen der Phasenmodulation (PM) und der Frequenzmodulation (FM) substanzielle Gemeinsamkeiten gibt. Man fasst deshalb diese beiden verwandten Modulationsverfahren unter dem Oberbegriff „Winkelmodulation” zusammen.

$\rm Definition\text{:}$  Eine Winkelmodulation – abgekürzt WM – liegt immer dann vor, wenn sich das modulierte Signal wie folgt darstellen lässt:

$$s(t) = A_{\rm T} \cdot \cos(\psi(t)) = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$

Hierbei bezeichnet $A_{\rm T}$ wie bei der Amplitudenmodulation die Amplitude des Trägersignals $z(t)$. Die gesamte Information über das Quellensignal $q(t)$ steckt nun aber in der Winkelfunktion $ψ(t)$.

Äquivalentes Tiefpass–Signal bei Winkelmodulation

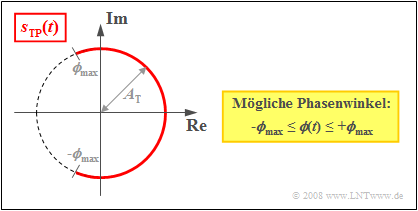
Anhand der Darstellung des äquivalenten Tiefpass–Signals $s_{\rm TP}(t)$ in der komplexen Ebene (wir bezeichnen eine solche Grafik als „Ortskurve”) sind folgende Charakteristika der Winkelmodulation zu erkennen:

• Die Ortskurve ist ein Kreisbogen mit dem Radius $A_{\rm T}$. Daraus folgt, dass die Hüllkurve eines winkelmodulierten Signals stets konstant ist:

$$a(t) = |s_{\rm TP}(t)|= A_{\rm T}= {\rm const.}$$

• Das äquivalente Tiefpass–Signal ist bei Winkelmodulation immer komplex und durch eine zeitabhängige Phasenfunktion $ϕ(t)$ (in Radian) festgelegt, welche die Nulldurchgänge von $s(t)$ bestimmt:

$$s_{\rm TP}(t)= A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm}.$$

• Bei symmetrischem Quellensignal $q(t)$ kann $ϕ(t)$ alle Werte zwischen $±ϕ_{\rm max}$ annehmen, wobei $ϕ_{\rm max}$ den Phasenhub angibt. Je größer der Phasenhub ist, desto intensiver ist die Modulation.
• Bei einer harmonischen Schwingung ist der Phasenhub $ϕ_{\rm max}$ gleich dem Modulationsindex $η$. Die Verwendung von $η$ zeigt im Folgenden also gleichzeitig an, dass $q(t)$ nur eine einzige Frequenz beinhaltet.
• Der Zusammenhang zwischen Quellensignal $q(t)$ und Winkelfunktion $ψ(t) = \cos[ω_{\rm T} · t + ϕ(t)]$ bzw. der daraus ableitbaren Phasenfunktion $ϕ(t)$ unterscheidet sich bei der Phasen– und der Frequenzmodulation grundsätzlich, worauf im Kapitel Frequenzmodulation noch ausführlich eingegangen wird.

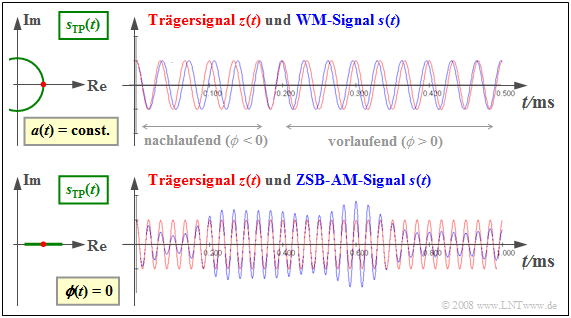
$\text{Beispiel 1:}$  Die folgende Grafik zeigt jeweils rechts das Sendesignal $s(t)$   ⇒   blaue Signalverläufe im Vergleich zum Trägersignal $z(t)$   ⇒   rote Schwingungen sowie links das äquivalente Tiefpass–Signal $s_{\rm TP}(t)$ in der komplexen Ebene. Diese Darstellung in der komplexen Ebene bezeichnen wir auch als die „Ortskurve”   ⇒   grüne Kurvenverläufe.

Physikalisches und äquivalentes TP–Signal bei Winkel- und Amplitudenmodulation

Die obere Skizze gilt für die Winkelmodulation (WM). In diesem Fall beschreibt das äquivalente TP–Signal $s_{\rm TP}(t) = A_{\rm T} · {\rm e}^{ {\rm j}·ϕ(t)}$ einen Kreisbogen, und es ergibt sich eine konstante Einhüllende $a(t) = A_{\rm T}$.

• Die Information über das Quellensignal $q(t)$ steckt bei der Winkelmodulation ausschließlich in der Lage der Nulldurchgänge von $s(t)$.
• Gilt momentan $ϕ(t) < 0$, so treten die Nulldurchgänge von $s(t)$ später als diejenigen von $z(t)$ auf. Andernfalls – bei $ϕ(t) > 0$ – sind die Nulldurchgänge von $s(t)$ gegenüber $z(t)$ vorlaufend.

Die untere Skizze gilt für die im zweiten Kapitel ausführlich behandelte Zweiseitenband–Amplitudenmodulation (ZSB-AM), gekennzeichnet durch

• die zeitabhängige Hüllkurve $a(t)$ entsprechend dem Quellensignal $q(t)$,
• äquidistante Nulldurchgänge von $s(t)$ gemäß dem Trägersignal $z(t)$, und
• eine horizontale Gerade als Ortskurve $s_{\rm TP}(t)$.

Das vorliegende dritte Kapitel wurde nach folgenden Gesichtspunkten gegliedert:

• Ein jedes FM–System kann durch einfache Modifikationen in ein entsprechendes PM–System übergeführt werden und umgekehrt.
• Größere Bedeutung bei Analogsystemen hat die FM aufgrund des günstigeren Rauschverhaltens. Deshalb werden Realisierungsaspekte für Modulator/Demodulator erst im Kapitel Frequenzmodulation (FM) behandelt.
• Die Phasenmodulation (PM) ist gegenüber der FM leichter zu verstehen. Deshalb werden zunächst in diesem ersten Kapitel die grundlegenden Eigenschaften eines Winkelmodulationssystems am Beispiel der PM dargelegt.

Signalverläufe bei Phasenmodulation

Ohne Einschränkung der Allgemeingültigkeit wird im Folgenden stets vorausgesetzt:

• ein cosinusförmiges Trägersignal $z(t) = A_{\rm T} · \cos(ω_{\rm T} · t)$, das heißt die Trägerphase $ϕ_{\rm T} =$ 0,
• ein spitzenwertbegrenztes Quellensignal in den Grenzen $\ –q_{\rm max} ≤ q(t) ≤ +q_{\rm max}$.

$\rm Definition\text{:}$  Ist die Phasenfunktion $ϕ(t)$ proportional dem anliegenden Quellensignal $q(t)$, so spricht man von einer Phasenmodulation (PM), und es gilt:

$$\phi(t)= K_{\rm PM} \cdot q(t)\hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\psi(t)= \omega_{\rm T} \cdot t + \phi(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \cos (\psi(t))\hspace{0.05cm}.$$

Hierbei bezeichnet $K_{\rm PM}$ die dimensionsbehaftete Modulatorkonstante. Beschreibt das Quellensignal $q(t)$ einen Spannungsverlauf, so besitzt diese Konstante die Einheit 1/V.

Die Phasenmodulaton ist um so intensiver,

• je größer die Modulatorkonstante $K_{\rm PM}$, und
• je größer der Maximalwert $q_{\rm max}$ des Quellensignals ist.

Quantitativ erfasst wird dieser Sachverhalt durch den Phasenhub

$$\phi_{\rm max} = K_{\rm PM} \cdot q_{\rm max}\hspace{0.05cm}.$$

Bei einer harmonischen Schwingung wird der Phasenhub auch als Modulationsindex bezeichnet und es gilt mit der Amplitude $A_{\rm N}$ des Quellensignals:

$$\eta = \eta_{\rm PM} = K_{\rm PM} \cdot A_{\rm N}\hspace{0.05cm}.$$

Zu dieser Gleichung ist Folgendes anzumerken:

• Der Modulationsindex $η$ ist vergleichbar mit dem Modulationsgrad $m$ bei ZSB–AM mit Träger.
• In der Ortskurve beschreiben $ϕ_{\rm max}$ bzw. $η$ den halben Winkel des Kreisbogens in „Radian”.
• Bei anderem Quellensignal mit gleichem $η$ – zum Beispiel bei anderer Nachrichtenphase $ϕ_{\rm N}$ – ändert sich die Ortskurve nicht, lediglich die zeitliche Bewegung auf der Ortskurve.
• Der Modulationsindex wird auch zur Beschreibung der Frequenzmodulation herangezogen, doch ist er dann etwas unterschiedlich zu berechnen. Wir unterscheiden deshalb zwischen $η_{\rm PM}$ und $η_{\rm FM}$.

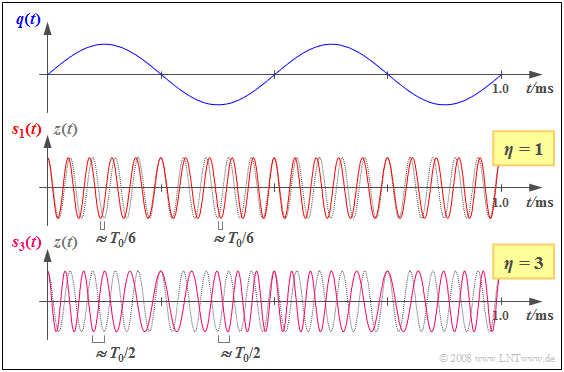
$\rm Beispiel \ 2\text{:}$  Die Grafik zeigt oben das sinusförmige Quellensignal $q(t)$ mit der Frequenz $f_{\rm N} = 2 \ \rm kHz$ und der Amplitude $A_{\rm N}$ sowie zwei phasenmodulierte Signale. Diese unterscheiden sich durch den Parameter $η = 1$ bzw. $η = 3$:

$$s_\eta(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t) \right)\hspace{0.05cm}.$$

Grau gepunktet ist jeweils das cosinusförmige Trägersignal $z(t)$ eingezeichnet, wobei $(f_{\rm T} = 20 \ \rm kHz$ zugrunde liegt.

Signalverläufe bei Phasenmodulation mit $η = 1$ bzw. $η = 3$

Der Modulationsindex $η = 1$ und damit das Sendesignal $s_1(t)$ ergibt sich zum Beispiel mit $A_{\rm N} = 1 \ \rm V$und $K_{\rm PM} = \rm 1/V$, aber auch mit den Parameterwerten $A_{\rm N} = 2 \ \rm V$ und $K_{\rm PM} = \rm 0.5/V$.

• Man erkennt, dass die Nulldurchgänge des Sendesignals $s_1(t)$ und des Trägersignals $z(t)$ genau dann übereinstimmen, wenn $q(t) ≈$ 0 ist.
• Bei $q(t) = +A_{\rm N}$ kommen die Nulldurchgänge von $s_1(t)$ um $1/(2π) ≈ 0.159$ einer Trägerperiode $T_0$ früher („vorlaufend”), bei $q(t) = \ –A_{\rm N}$ um den gleichen Bruchteil später („nachlaufend”).
• Erhöht man den Modulationsindex – entweder durch Verdreifachung von $A_{\rm N}$ oder von $K_{\rm PM}$ – auf $η = 3$, so ergibt sich qualitativ das gleiche Resultat, aber eine intensivere Phasenmodulation.
• Die Nulldurchgänge des Signals $s_3(t)$ sind gegenüber denen des Taktsignals nun um maximal $\rm ±3/(2π) ≈ ±0.5$ einer Trägerperiode verschoben, also bis zu $±T_0/2$.

Äquivalentes TP–Signal bei Phasenmodulation

Als Vorbereitung zur Herleitung des Spektrums $S(f)$ eines phasenmodulierten Signals $s(t)$ wird zunächst das äquivalente TP–Signal $s_{\rm TP}(t)$ analysiert. Dabei gehen wir von folgenden Voraussetzungen aus:

• ein sinusförmiges Quellensignal mit Amplitude $A_{\rm N}$ und Frequenz $f_{\rm N}$,
• ein cosinusförmiges Trägersignal mit Amplitude $A_{\rm T}$ und Frequenz $f_{\rm T}$,
• eine Phasenmodulation mit dem Modulationsindex $η = K_{\rm PM} · A_{\rm N}$.

Damit lauten das phasenmodulierte Signal sowie das dazugehörige äquivalente Tiefpass–Signal:

$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t) \right)\hspace{0.05cm},\hspace{0.5cm}s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm N} \cdot t) }\hspace{0.05cm}.$$

Dieses Signal ist periodisch und kann somit durch eine komplexe Fourierreihe dargestellt werden. Damit erhält man allgemein:

$$s_{\rm TP}(t) = \sum_{n = - \infty}^{+\infty}D_{n} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t} \hspace{0.05cm}.$$

In dem hier betrachteten Sonderfall (sinusförmiges Quellensignal, cosinusförmiger Träger) sind die im Allgemeinen komplexen Fourierkoeffizienten $D_n$ alle reell und mit den Besselfunktionen $J_n(η)$ erster Art und n–ter Ordnung wie folgt gegeben:

$$D_{n} = A_{\rm T}\cdot {\rm J}_n (\eta) \hspace{0.05cm}. \hspace{1cm}$$

{{BlaueBox|TEXT= $\text{Wichtiges Zwischenergebnis:}$  Nun soll mathematisch nachgewiesen werden, dass das äquivalente Tiefpass–Signal bei Phasenmodulation tatsächlich in die folgende Funktionsreihe umgewandelt werden kann:

$$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm N} \cdot t) } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s_{\rm TP}(t) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

$\text{Beweis:}$  Wir setzen vereinfachend $A_{\rm T} = 1$. Damit lautet das gegebene äquivalente Tiefpass–Signal:   $s_{\rm TP}(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm N} \cdot t) }\hspace{0.05cm}.$

1. Mit $x = {\rm j} · η · \sin(γ)$ und $γ = ω_{\rm N} · t$ lautet die Potenzreihenentwicklung dieser Gleichung:

$$s_{\rm TP}(t) = {\rm e}^{x } = 1 + x + \frac{1}{2!} \cdot x^2 + \frac{1}{3!} \cdot x^3 + \text{...} = 1 + {\rm j} \cdot \eta \cdot \sin (\gamma)+ \frac{1}{2!} \cdot {\rm j}^2 \cdot \eta^2 \cdot \sin^2 (\gamma)+ \frac{1}{3!} \cdot {\rm j}^3 \cdot \eta^3 \cdot \sin^3 (\gamma) + \text{...}$$

2. Die einzelnen trigonometrischen Ausdrücke können wie folgt umgeformt werden:

$$\frac{1}{2!} \cdot {\rm j}^2 \cdot \eta^2 \cdot \sin^2 (\gamma) = \frac{- \eta^2}{2 \cdot 2!} \cdot \left[ 1 - \cos (2\gamma)\right],\hspace{1.0cm} \frac{1}{3!} \cdot {\rm j}^3 \cdot \eta^3 \cdot \sin^3 (\gamma) = \frac{- {\rm j} \cdot \eta^3}{4 \cdot 3!} \cdot \left[ 3 \cdot \sin (\gamma)- \sin (3\gamma)\right],$$

$$\frac{1}{4!} \cdot {\rm j}^4 \cdot \eta^4 \cdot \sin^4 (\gamma) = \frac{\eta^4}{8 \cdot 4!} \cdot \left[ 3+ 4 \cdot \cos (2\gamma)+ \cos (4\gamma)\right], \text{...}$$

3. Durch Umordnen erhält man mit $J_n(η)$, den Besselfunktionen erster Art und $n$–ter Ordnung:

$$s_{\rm TP}(t) = 1 \cdot {\rm J}_0 (\eta) + 2 \cdot {\rm j}\cdot {\rm J}_1 (\eta)\cdot \sin (\gamma) \hspace{0.2cm} + 2 \cdot {\rm J}_2 (\eta)\cdot \cos (2\gamma) + 2 \cdot {\rm j}\cdot {\rm J}_3 (\eta)\cdot \sin (3\gamma)+ 2 \cdot {\rm J}_4 (\eta)\cdot \cos (4\gamma) + \text{...}$$

4. Mit dem Satz von Euler kann hierfür auch geschrieben werden:

$$s_{\rm TP}(t) = {\rm J}_0 (\eta) + \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} \right]\cdot {\rm J}_1 (\eta) \hspace{0.27cm} +\left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} \right]\cdot {\rm J}_2 (\eta)+ \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 3\gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 3\gamma} \right]\cdot {\rm J}_3 (\eta)+ \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 4\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 4\gamma} \right]\cdot {\rm J}_4 (\eta)+\text{...}$$

5. Die Besselfunktionen zeigen folgende Symmetrieeigenschaften:

$${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm J}_{-1} (\eta) = -{\rm J}_{1} (\eta),\hspace{0.3cm}{\rm J}_{-2} (\eta) = {\rm J}_{2} (\eta),\hspace{0.3cm}{\rm J}_{-3} (\eta) = -{\rm J}_{3} (\eta),\hspace{0.3cm}{\rm J}_{-4} (\eta) = {\rm J}_{4} (\eta).$$

6. Berücksichtigt man diesen Sachverhalt und den bisher weggelassenen Faktor $A_{\rm T}$, so erhält man das gewünschte Ergebnis:

$$s_{\rm TP}(t) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$ }}

Diese bereits 1844 von Friedrich Wilhelm Bessel eingeführten mathematischen Funktionen sind wie folgt definiert (erste Gleichung) und können gemäß der zweiten Gleichung durch eine Reihe angenähert werden:

Zur Berechnung der Besselfunktionen

$${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$

Die nebenstehende Grafik zeigt die jeweils ersten drei Summanden $(k = 0, 1, 2)$ der Reihen $J_0(η)$, ... , $J_3(η).$ Der rot umrandete Term – gültig für $n = 3$ und $k = 2$ – lautet beispielsweise in ausgeschriebener Form:

$$\frac{(-1)^2 \cdot (\eta/2)^{3 \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}2}}{2\hspace{0.05cm}! \cdot (3+2)\hspace{0.05cm}!} = \frac{1}{240}\cdot (\frac{\eta}{2})^7 \hspace{0.05cm}.$$

• Die Besselfunktionen $J_n(η)$ findet man aber auch in Formelsammlungen oder mit Hilfe des von uns bereitgestellten Berechnungsmodul Werte der Besselfunktion erster Art und n–ter Ordnung.
• Sind die Funktionswerte für $n = 0$ und $n = 1$ bekannt, so können daraus die Besselfunktionen für $n ≥ 2$ iterativ ermittelt werden:

$${\rm J}_n (\eta) ={2 \cdot (n-1)}/{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$

Interpretation des Besselspektrums

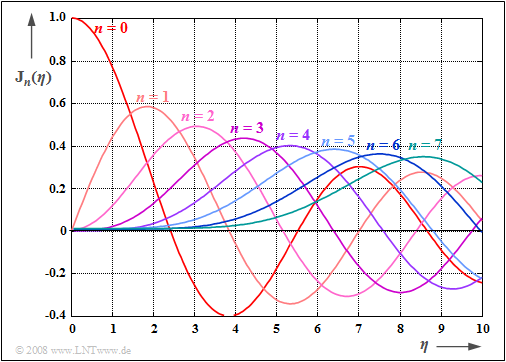
Die Grafik zeigt die Besselfunktionen $J_0(η)$, ... , $J_7(η)$ abhängig vom Modulationsindex $η\ (0 ≤ η ≤ 10)$.

Besselfunktionen erster Art und n–ter Ordnung

Man findet diese auch in Formelsammlungen wie [BS01] in tabellarischer Form. Die erste Art wird durch das „J” ausgedrückt, die Ordnung durch den Index.

Anhand dieser Grafik können für das äquivalente Tiefpass-Signal

$$s_{\rm TP}(t) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}$$

folgende Eigenschaften abgeleitet werden:

• Das äquivalente TP–Signal setzt sich aus einem ruhenden Zeiger ($n = 0$) sowie unendlich vielen im Uhrzeigersinn ($n < 0$) bzw. entgegen dem Uhrzeigersinn ($n > 0$) drehenden Zeigern zusammen.

• Die Zeigerlängen hängen über die Besselfunktionen $J_n(η)$ vom Modulationsindex $η$ ab. Je kleiner $η$ ist, um so mehr Zeiger können allerdings für die Konstruktion von $s_{\rm TP}(t)$ vernachlässigt werden.

• Für den Modulationsindex $η =$ 1 gilt beispielsweise folgende Näherung:

$$s_{\rm TP}(t) = {\rm J}_0 (1) + {\rm J}_1 (1)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}+ {\rm J}_2 (1)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}+ {\rm J}_3 (1)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}3 \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}- {\rm J}_1 (1)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}+ {\rm J}_2 (1)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}2 \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}- {\rm J}_3 (1)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}3 \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm} t}\hspace{0.05cm}.$$

• Hierbei ist die Symmetriebeziehung $J_{–n}(η) = (–1)^n · J_n(η)$ berücksichtigt. Es gilt also:

$${\rm J}_{-1}(\eta) = - {\rm J}_{1}(\eta), \hspace{0.3cm}{\rm J}_{-2}(\eta) = {\rm J}_{2}(\eta), \hspace{0.3cm}{\rm J}_{-3}(\eta) = - {\rm J}_{3}(\eta).$$

• Weiter erkennt man aus obiger Gleichung, dass sich $s_{\rm TP}(t)$ mit $η = 3$ aus deutlich mehr Zeigern (nämlich mit den Indizes $J_{–6}(\eta)$, ... , $J_{+6}(\eta)$ zusammensetzen würde.

{{GraueBox|TEXT= $\rm Beispiel\ 3\text{:}$  Die Besselfunktionen liefern für den Modulationsindex $η = 1$ folgende Zahlenwerte:

$${\rm J}_0 = 0.765,\hspace{0.3cm}{\rm J}_1 = -{\rm J}_{-1} = 0.440, \hspace{0.3cm}{\rm J}_2 = {\rm J}_{-2} = 0.115,\hspace{0.3cm}{\rm J}_3 = -{\rm J}_{-3} = 0.020\hspace{0.05cm}.$$

Äquivalentes Tiefpass–Signal bei Phasenmodulation

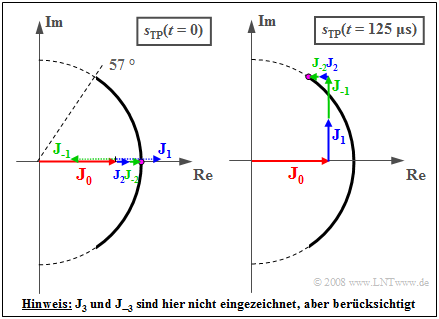
Die Grafik zeigt die Zusammensetzung der Ortskurve aus den sieben Zeigern ($J_3$ und $J_{-3}$ fehlen in der Skizze, aber nicht im Gesamtsignal).

Die Frequenz des sinusförmigen Quellensignals ist $f_{\rm N} = 2 \ \rm kHz$, woraus sich die Periodendauer $T_{\rm N} = 1/f_{\rm N} = 500 \ \rm μs$ ergibt. Vereinfachend wird $A_{\rm T} = 1$ gesetzt.

Das linke Bild zeigt die Momentaufnahme zur Zeit $t = 0$.

• Wegen $J_1 = \ –J_{–1}$ und $J_3 = \ –J_{–3}$ gilt hierfür:

$$s_{\rm TP}(t = 0) = {\rm J}_0 + {\rm J}_{2} + {\rm J}_{-2} = 0.765 + 2 \cdot 0.115 = 0.995 \hspace{0.05cm}.$$

• Aus dem reellen Ergebnis folgt die Phase ${\mathbf ϕ}(t = 0) = 0$ und der Betrag $a(t = 0) = 1$.
• Der geringfügig abweichende Wert $0.995$ zeigt, dass $J_4 = J_{–4}$ zwar sehr klein $(≈ 0.002)$ ist, aber nicht identisch $0$.

Das rechte Bild zeigt die Verhältnisse zur Zeit $t = T_{\rm N}/4 = 125\ \rm μs$:

• Die Zeiger mit den Längen $J_{–1}$ und $J_1$ haben sich im bzw. entgegen dem Uhrzeigersinn um $90^\circ$ gedreht und zeigen nun beide in Richtung der imaginären Achse.
• Die Zeiger $J_2$ und $J_{–2}$ drehen doppelt so schnell wie $J_1$ bzw. $J_{–1}$ und zeigen nun beide in Richtung der negativen reellen Achse.
• $J_3$ und $J_{–3}$ drehen im Vergleich zu $J_1$ und $J_{–1}$ mit dreifacher Geschwindigkeit und zeigen jetzt beide nach unten.

Damit erhält man:

$$s_{\rm TP}(t = 125\,{\rm \mu s}) = {\rm J}_0 - 2 \cdot {\rm J}_{2} + {\rm j} \cdot (2 \cdot {\rm J}_{1}-2 \cdot {\rm J}_{3})= 0.535 + {\rm j} \cdot 0.840$$

$$\Rightarrow \hspace{0.3cm} a(t = 125\,{\rm \mu s}) = \sqrt{0.535^2 + 0.840^2}= 0.996\hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm}\phi(t = 125\,{\rm \mu s}) = \arctan \frac{0.840}{0.535} = 57.5^\circ \approx 1\,{\rm rad}\hspace{0.05cm}.$$

Auch zu allen anderen Zeitpunkten ergibt die vektorielle Summe der sieben Zeiger jeweils einen Punkt auf dem Kreisbogen mit Winkel $ϕ(t)$, wobei $\vert ϕ(t) \vert ≤ η = 1\ \rm rad$ gilt. }}

Spektralfunktion eines phasenmodulierten Sinussignals

Ausgehend vom eben berechneten äquivalenten Tiefpass–Signal erhält man für das analytische Signal:

$$s_{\rm +}(t) = s_{\rm TP}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T} \hspace{0.05cm}\cdot \hspace{0.05cm} t}= A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}(\omega_{\rm T}\hspace{0.05cm}+\hspace{0.05cm} n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N}) \hspace{0.05cm}\cdot \hspace{0.05cm} t}$$

Durch Fouriertransformation ergibt sich für das Spektrum des analytischen Signals:

$$S_{\rm +}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta [f - (f_{\rm T}+ n \cdot f_{\rm N})]\hspace{0.05cm}.$$

Das Spektrum des physikalischen Signals erhält man durch Ausweitung auf negative Frequenzen unter Berücksichtigung des Faktors 1/2:

$$S(f) = \frac{A_{\rm T} }{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta [f \pm (f_{\rm T}+ n \cdot f_{\rm N})]\hspace{0.05cm}.$$

Spektrum des analytischen Signals bei PM (auch bei FM)

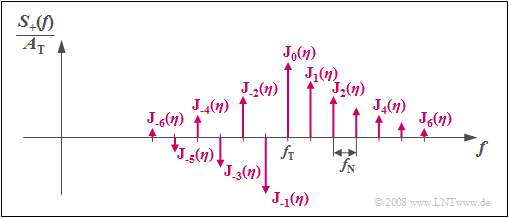
Anhand der Grafik sind folgende Aussagen möglich:

• Das Spektrum $S_+(f)$ eines phasenmodulierten Sinussignals besteht aus unendlich vielen diskreten Linien im Abstand der Nachrichtenfrequenz $f_{\rm N}$. Es ist somit prinzipiell unendlich weit ausgedehnt.
• Die Höhen (Gewichte) der Spektrallinien bei $f_{\rm T} + n · f_{\rm N}$ (wobei $n$ ganzzahlig ist) sind durch den Modulationsindex $η$ über die Besselfunktionen $J_n(η)$ festgelegt.
• Die Werte der Besselfunktionen $J_n(η)$ zeigen, dass man in der Praxis durch Bandbegrenzung das Spektrum nur wenig verändert. Der daraus resultierende Fehler wächst aber mit steigendem $η$.
• Die Spektrallinien sind bei sinusförmigem Quellensignal und cosinusförmigem Träger reell und für gerades $n$ symmetrisch um $f_{\rm T}$. Bei ungeradem $n$ ist ein Vorzeichenwechsel zu berücksichtigen.
• Die Phasenmodulation einer Schwingung mit anderer Phase von Quellen– und/oder Trägersignal liefert das gleiche Betragsspektrum und unterscheidet sich nur bezüglich der Phasenfunktion.
• Setzt sich das Nachrichtensignal aus mehreren Schwingungen zusammen, so ist die Berechnung des Spektrums schwierig (Faltung der Einzelspektren, siehe nächster Abschnitt und Aufgabe 3.3).

Phasenmodulation der Summe zweier Sinusschwingungen

Setzt sich das Quellensignal aus der Summe zweier Sinusschwingungen zusammen, so lauten die Signale am Ausgang des Phasenmodulators:

$$s(t) = A_{\rm T} \cdot \cos \left[\omega_{\rm T} \cdot t + \eta_1 \cdot \sin (\omega_{\rm 1} \cdot t) + \eta_2 \cdot \sin(\omega_{\rm 2} \cdot t)\right]\hspace{0.05cm},$$

$$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot [\hspace{0.05cm}\eta_1 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (\omega_{\rm 1} \hspace{0.05cm}\cdot \hspace{0.05cm} t) \hspace{0.05cm}+ \hspace{0.05cm}\eta_2 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (\omega_{\rm 2} \hspace{0.05cm}\cdot \hspace{0.05cm}t)]}\hspace{0.05cm}.$$

Zur einfacheren Darstellung setzten wir nun $A_{\rm T} = 1$ und erhalten:

$$s_{\rm TP}(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta_1 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (\omega_{\rm 1} \hspace{0.05cm}\cdot \hspace{0.05cm} t) } \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta_2 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (\omega_{\rm 2} \hspace{0.05cm}\cdot \hspace{0.05cm} t) }\hspace{0.05cm}.$$

Die Spektralfunktionen der beiden Terme lauten:

$${\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta_1 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm 1} \hspace{0.01cm}\cdot \hspace{0.05cm} t) } \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} B_1(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta_1) \cdot \delta (f - n \cdot f_{\rm 1})\hspace{0.05cm},$$

$${\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta_2 \hspace{0.05cm}\cdot \hspace{0.08cm}\sin (2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm 2} \hspace{0.01cm}\cdot \hspace{0.05cm} t) } \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} B_2(f) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta_2) \cdot \delta (f - n \cdot f_{\rm 2})\hspace{0.05cm}.$$

Die beiden Besselfunktionen $B_1(f)$ und $B_2(f)$ beschreiben Linienspektren im Frequenzabstand $f_1$ und $f_2$, deren Impulsgewichte durch $η_1$ und $η_2$ bestimmt sind. Aufgrund der Multiplikation im Zeitbereich ergibt sich für die Spektralfunktion die Faltung:

$$S_{\rm TP}(f) = B_1(f) \star B_2(f)= S_{\rm +}(f + f_{\rm T}) \hspace{0.05cm}.$$

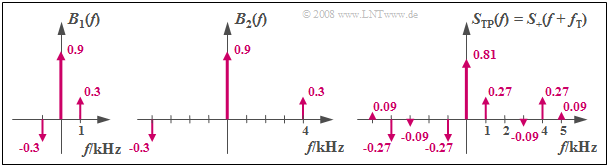
$\rm Beispiel\ 4\text{:}$  Die linke Grafik zeigt die Besselfunktion $B_1(f)$ für $η_1 = 0.64$ und $f_1 = 1 \ \rm kHz$; auf die Linien bei $f = ±2 \ \rm kHz$ mit denGewichten $0.05$ ist der Übersichtlichkeit halber verzichtet.
Die Funktion $B_2(f)$ gilt für den gleichen Modulationsindex $η_2 = η_1$, aber für die Nachrichtenfrequenz $f_2 = 4 \ \rm kHz$.

Äquivalentes Tiefpass-Spektrum als Faltung zweier Besselspektren

• Das Tiefpass-Spektrum $S_{\rm TP}(f) = B_1(f) \star B_2(f)$ besteht hier aus neun Diraclinien. Es ist im rechten Diagramm skizziert.
• Durch Frequenzverschiebung um die Trägerfrequenz $f_{\rm T}$ nach rechts erhält man das Spektrum $S_+(f)$ des analytischen Signals $s_+(t)$.

Aufgaben zum Kapitel

Aufgabe 3.1:   Ortskurve bei Phasenmodulation

Zusatzaufgabe 3.1Z:   Einfluss der Nachrichtenphase bei PM

Aufgabe 3.2:   Spektrum bei Winkelmodulation

Zusatzaufgabe 3.2Z:   Besselspektrum

Aufgabe 3.3:   Summe zweier Schwingungen

Zusatzaufgabe 3.3Z:   Kenngrößenbestimmung

Aufgabe 3.4:   Einfacher Phasenmodulator