Wiener–Kolmogorow–Filter

1. Stochastische Signaltheorie
2. Filterung stochastischer Signale
3. Wiener–Kolmogorow–Filter

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Optimierungskriterium des Wiener–Kolmogorow–Filters

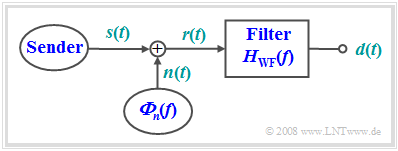
Als weiteres Beispiel zur Optimalfilterung betrachten wir nun die Aufgabenstellung, die Form eines Nutzsignals $s(t)$ aus dem durch additives Rauschen $n(t)$ gestörten Empfangssignals $r(t)$ im Sinne des mittleren quadratischen Fehlers (MQF) möglichst gut zu rekonstruieren: $${\rm{MQF}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t} \mathop = \limits^! {\rm{Minimum}}.$$

Das entsprechende Filter ist nach seinen Erfindern Norbert Wiener und Andrei Nikolajewitsch Kolmogorow benannt. Den entsprechenden Frequenzgang bezeichnen wir mit $H_{\rm WF}(f).$

Für diese Optimierungsaufgabe gelten folgende Voraussetzungen:

• Das zu rekonstruierende Signal $s(t)$ ist das Ergebnis eines Zufallsprozesses { $s(t)$}, von dem nur die statistischen Eigenschaften in Form des Leistungsdichtespektrums ${\it Φ}_s(f)$ bekannt ist.
• Das Störsignal $n(t)$ ist durch das LDS ${\it Φ}_n(f)$ gegeben. Korrelationen zwischen dem Nutz– und dem Störsignal berücksichtigen die Kreuzleistungsdichtespektren ${\it Φ}_{sn}(f) = \hspace{0.1cm} –{ {\it Φ}_{ns} }^∗(f).$
• Das Ausgangssignal des gesuchten Filters ist mit $d(t)$ bezeichnet, das sich entsprechend des MQF möglichst wenig von $d(t)$ unterscheiden soll. $T_{\rm M}$ bezeichnet wiederum die Messdauer.

Zur Herleitung des Wiener-Filters

Das Signal $s(t)$ sei mittelwertfrei $(m_s = 0)$ und leistungsbegrenzt. Das bedeutet: Die Signalenergie $E_s$ ist aufgrund der unendlichen Ausdehnung des Signals $s(t)$ unendlich und die Signalleistung besitzt einen endlichen Wert:

$$P_s = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{{T_{\rm M} }}\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {s(t)^2 \, {\rm{d}}t > 0.}$$

Ein grundsätzlicher Unterschied zur Aufgabenstellung beim Matched–Filter ist das stochastische und leistungsbegrenzte Nutzsignal $s(t)$. Erinnern wir uns: Beim Matched–Filter war das zu rekonstruierende Signal $g(t)$ deterministisch, zeitlich begrenzt und damit auch energiebegrenzt.

Ergebnis der Filteroptimierung

A. Kolmogorow und N. Wiener haben dieses Optimierungsproblem nahezu zur gleichen Zeit unabhängig voneinander gelöst. Die Übertragungsfunktion des optimalen Filters kann über die so genannte Wiener-Hopfsche Integralgleichung ermittelt werden, und lautet:

$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) + {\it \Phi }_{ns} (f)} }{ { {\it \Phi }_s (f) + {\it \Phi }_{sn} (f) + {\it \Phi }_{ns} (f) + {\it \Phi }_n (f)}}.$$

Der Index „WF” steht für Wiener-Filter und lässt leider die Verdienste von Kolmogorow nicht erkennen. Auf die exakte, mathematische Ableitung der Gleichung wird hier verzichtet. Vielmehr soll dieses Filter im Folgenden an einigen Sonderfällen verdeutlicht und interpretiert werden.

• Sind Signal und Störung unkorreliert ⇒ ${\it Φ}_{sn}(f) = {\it Φ}_{ns}(f) = 0$, so vereinfacht sich die obige Gleichung wie folgt:

$$H_{\rm WF} (f) = \frac{{ {\it \Phi }_s (f) }}{{ {\it \Phi }_s (f) + {\it \Phi }_n (f) }} = \frac{1}{{1 + {\it \Phi }_n (f) / {\it \Phi }_s (f) }}.$$

• Das Filter wirkt dann wie ein frequenzabhängiger Teiler, wobei das Teilerverhältnis durch die Leistungsdichtespektren von Nutzsignal und Störsignal bestimmt wird.
• Der „Durchlassbereich” liegt vorwiegend bei den Frequenzen, bei denen das Nutzsignal sehr viel größere Anteile besitzt als die Störung: ${\it Φ}_s(f) \gg {\it Φ}_n(f).$
• Der mittlere quadratische Fehler (MQF) zwischen dem Filterausgangssignal $d(t)$ und dem zu approximierenden Eingangssignal $s(t)$ ist

$${\rm MQF} = \int\limits_{ - \infty }^{ + \infty } {\frac{{ {\it \Phi }_s (f) \cdot {\it \Phi }_n (f)}}{{ {\it \Phi }_s(f) + {\it \Phi }_n (f)}}\,{\rm{d}}f = \int\limits_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi }_n (f)}\, {\rm{d}}f.}$$

Die Herleitung dieser Ergebnisse ist durchaus nicht trivial und zum Beispiel in [Hän97] zu finden.

Interpretation des Wiener-Filters

In diesem Abschnitten wird das Wiener–Kolmogorow–Filter anhand zweier Beispiele verdeutlicht.

Beispiel 1:  Zur Verdeutlichung des Wiener–Filters betrachten wir zunächst als Grenzfall ein Sendesignal $s(t)$ mit dem LDS ${\it Φ}_s(f) = P_s · δ(f ± f_s).$

• Damit ist bekannt, dass $s(t)$ eine harmonische Schwingung mit der Frequenz $f_s$ ist.
• Unbekannt sind dagegen Amplitude und Phase der aktuellen Musterfunktion $s(t)$.

Bei weißem Rauschen ⇒ ${\it Φ}_n(f) = N_0/2$ – lautet somit der Frequenzgang des Wiener-Filters:

$$H_{\rm WF} (f) = \frac{1}{{1 +({N_0 /2})/{( P_s \cdot\delta ( {f \pm f_s } )}})}.$$

• Bei allen Frequenzen mit Ausnahme von $f = ±f_s$ ergibt sich $H_{\rm WF}(f) = 0$, da hier der Nenner unendlich groß wird.
• Berücksichtigt man weiter, dass $δ(f = ±f_s)$ an der Stelle $f = ±f_s$ unendlich groß ist, so erhält man weiter $H_{\rm MF}(f = ±f_s ) = 1. $
• Das optimale Filter ist somit ein Bandpass um $f_s$ mit unendlich kleiner Bandbreite. Der mittlere quadratische Fehler zwischen dem Sendesignal $s(t)$ und dem Filterausgangssignal $d(t)$ beträgt

$${\rm{MQF}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f) \cdot {\it \Phi_n} (f) \,{\rm{d}}f = \mathop {\lim }\limits_{\varepsilon \hspace{0.03cm} {\rm > \hspace{0.03cm}0,}\;\;\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}\rm 0 } }\hspace{0.1cm} \int_{f_s - \varepsilon }^{f_s + \varepsilon }\hspace{-0.3cm} {N_0 }\,\,{\rm{d}}f = 0.$$

• Dieses unendlich schmale Bandpass–Filter würde bei den getroffenen Voraussetzungen die vollständige Regenerierung der Harmonischen hinsichtlich Amplitude und Phase erlauben. Unabhängig von der Größe der Störung $(N_0)$ würde somit $d(t) = s(t)$ gelten.
• Allerdings ist ein unendlich schmales Filter nicht realisierbar. Bei endlicher Bandbreite $Δf$ ist der mittlere quadratische Fehler (MQF) gleich $N_0 · Δf$.
  

Dieses Beispiel hat einen Sonderfall behandelt, bei dem das bestmögliche Ergebnis $\rm MQF = 0$ zumindest theoretisch möglich ist. Das folgende Beispiel geht von realistischeren Annahmen aus und liefert das Ergebnis $\rm MQF > 0$.

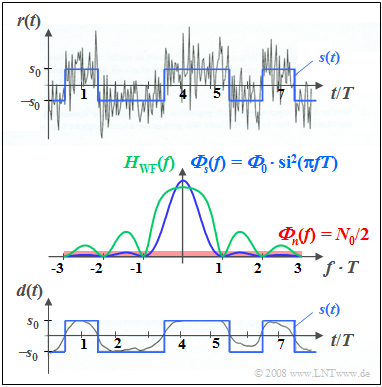
Beispiel 2:  Nun betrachten wir ein stochastisches rechteckförmiges Binärsignal $s(t)$, das durch weißes Rauschen $n(t)$ additiv überlagert ist. Die Grafik enthält folgende Diagramme:

Signale beim Wiener-Filter

• Oben ist grau das Summensignal $r(t) = s(t) + n(t)$ für ${\it Φ}_0/N_0 = 5$ dargestellt, wobei ${\it Φ}_0$ die Energie eines Einzelimpulses bezeichnet und $N_0$ die Rauschleistungsdichte des weißen Rauschens angibt.
• In Bildmitte sind die Leistungsdichtespektren ${\it Φ}_s(f)$ und ${\it Φ}_n(f)$ in blauer bzw. roter Farbe skizziert und formelmäßig angegeben. Grün gezeichnet ist der Frequenzgang $H_{\rm WF}(f)$.
• Das untere Bild zeigt als grauen Kurvenzug das Ausgangssignal $d(t)$ des Wiener-Filters im Vergleich zum blau gezeichneten Sendesignal $s(t)$. Im Idealfall sollte $d(t) = s(t)$ gelten.

Die untere Darstellung zeigt:

• Der mittlere quadratische Fehler (MQF) zwischen den Signalen $d(t)$ und $s(t)$ beträgt hier etwa 11% der Nutzleistung $P_s$.
• Im Signal $d(t)$ fehlen vorwiegend die höherfrequenten Signalanteile (also die Sprünge).
• Diese Anteile werden zugunsten einer besseren Störunterdrückung bei diesen Frequenzen ausgefiltert.

Mit keinem anderen Filter ergibt sich bei diesen Voraussetzungen ein kleinerer (mittlerer quadratischer) Fehler als mit dem Wiener-Filter. Dessen Frequenzgang lautet hier: $$H_{\rm WF} (f) = \frac{1}{{1 + ({N_0 /2})/( {\it \Phi}_0 \cdot {\rm si^2} ( \pi f T )})} \hspace{0.15cm} .$$

Aus dem mittleren Diagramm erkennt man:

• Der Gleichsignalübertragungsfaktor ergibt sich zu $H_{\rm WF}(f = 0) = {\it Φ}_0/({\it Φ}_0 + N_0/2) = 10/11.$
• Bei Vielfachen der Symbolfolgefrequenz $1/T$, bei denen das stochastische Nutzsignal $s(t)$ keine Spektralanteile besitzt, ist $H_{\rm WF}(f) = 0$.
• Je mehr Nutzsignalanteile bei einer bestimmten Frequenz vorhanden sind, desto durchlässiger ist bei dieser Frequenz auch das Wiener-Filter.

Aufgabe zum Kapitel

Aufgabe 5.9:   Minimierung des MQF