Zum Rechnen mit komplexen Zahlen
Inhaltsverzeichnis
Reelle Zahlenmengen
In den folgenden Kapiteln dieses Buches spielen komplexe Größen stets eine wichtige Rolle. Obwohl das Rechnen mit komplexen Zahlen bereits in der Schulmathematik behandelt und geübt wird, haben unsere Erfahrungen gezeigt, dass auch Studierende von naturwissenschaftlichen und technischen Fachgebieten damit durchaus Probleme haben. Vielleicht hängen diese Schwierigkeiten auch damit zusammen, dass „komplex” im Alltag oft als Synonym für „kompliziert” verwendet wird, während „reell” laut Duden für „zuverlässig, ehrlich und redlich” steht.
Deshalb werden hier am Ende dieses ersten Grundlagenkapitels die Rechenregeln für komplexe Zahlen kurz zusammengefasst.
Zunächst folgen einige Anmerkungen über reelle Zahlenmengen, für die im strengen mathematischen Sinne die Bezeichnung „Zahlenkörper” richtiger wäre. Hierzu gehören:
$\text{Definitionen:}$
- Natürliche Zahlen $\mathbb{N} = \{1, 2, 3, \text{...}\hspace{0.05cm} \}$. Mit diesen Zahlen sind für $n, \ k \in \mathbb{N}$ die Rechenoperationen „Addition” $(m = n +k)$, „Multiplikation” $(m = n \cdot k)$ und „Potenzbildung” $(m = n^k)$ möglich. Das jeweilige Ergebnis einer Rechenoperation ist wieder eine natürliche Zahl: $m \in \mathbb{N}$.
- Ganze Zahlen $\mathbb{Z} = \{\text{...}\hspace{0.05cm} , -3, -2, -1, \ 0, +1, +2, +3, \text{...}\hspace{0.05cm}\}$. Diese Zahlenmenge ist eine Erweiterung der natürlichen Zahlen $\mathbb{N}$. Die Einführung der Menge $\mathbb{Z}$ war notwendig, um die Ergebnismenge einer Substraktion $(m = n -k)$ zu erfassen, zum Beispiel $5 - 7 = - 2$.
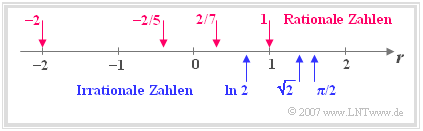
- Rationale Zahlen $\mathbb{Q} = \{z/n\}$ mit $z \in \mathbb{Z}$ und $n \in \mathbb{N}$. Mit dieser auch als Bruchzahlen bekannten Zahlenmenge liegt auch für jede Division ein definiertes Ergebnis vor. Schreibt man eine rationale Zahl in Dezimalschreibweise, so treten ab einer gewissen Dezimalstelle nur Nullen auf $($Beispiel: $-2/5 = -0.400\text{...}\hspace{0.05cm})$ oder es ergeben sich Periodizitäten $($Beispiel: $2/7 = 0.285714285\text{...}\hspace{0.05cm})$. Da $n = 1$ erlaubt ist, sind die ganzen Zahlen eine Teilmenge der rationalen Zahlen: $\mathbb{Z} \subset \mathbb{Q}$.
- Irrationale Zahlen $\mathbb{I} \neq {z/n}$ mit $z \in \mathbb{Z}$, $n \in \mathbb{N}$. Obwohl es unendlich viele rationale Zahlen gibt, verbleiben ebenfalls unendlich viele Zahlen, die nicht als Bruch dargestellt werden können. Beispiele hierfür sind die Zahl $\pi = 3.141592654\text{...}\hspace{0.05cm}$ (wobei es auch bei mehr Dezimalstellen keine Perioden gibt) oder das Ergebnis der Gleichung $a^{2}=2 \,\,\Rightarrow \;\;a=\pm \sqrt{2}=\pm1.414213562\text{...}\hspace{0.05cm}$. Auch dieses Ergebnis ist irrational, was bereits Euklid in der Antike bewiesen hat.
- Reelle Zahlen $\mathbb{R} = \mathbb{Q} \cup \mathbb{I}$ als die Gesamtheit aller rationalen und irrationalen Zahlen.
- Diese können entsprechend ihren Zahlenwerten geordnet und auf dem so genannten Zahlenstrahl eingezeichnet werden, wie die nebenstehende Grafik verdeutlicht.
Imaginäre und komplexe Zahlen
Mit der Einführung der irrationalen Zahlen war zwar die Lösung der Gleichung $a^2-2=0$ möglich, nicht jedoch die Lösung der Gleichung $a^2+1=0$.
Der Mathematiker Leonhard Euler löste dieses Problem, indem er den Körper der reellen Zahlen um die imaginären Zahlen erweiterte. Er definierte dazu die imaginäre Einheit wie folgt:
- $${\rm j}=\sqrt{-1} \ \Rightarrow \ {\rm j}^{2}=-1.$$
Anzumerken ist, dass Euler diese Größe mit „$\rm i$” bezeichnet hat und dies auch heute noch in der Mathematik so üblich ist. In der Elektrotechnik hat sich dagegen die Bezeichnung „$\rm j$” durchgesetzt, da „$\rm i$” bereits mit dem zeitabhängigen Strom belegt ist.
$\text{Definition:}$ Die komplexe Zahl $z$ ist im allgemeinen die Summe einer reellen Zahl $x$ und einer imaginären Zahl ${\rm j} \cdot y$:
- $$z=x+{\rm j}\cdot y.$$
$x$ und $y$ entstammen hierbei der Menge $\mathbb{R}$ der reellen Zahlen. Die Menge aller möglichen komplexen Zahlen bezeichnet man als den Körper $\mathbb{C}$ der komplexen Zahlen.
Aus dem Zahlenstrahl der reellen Zahlen wird nun die komplexe Ebene, die durch zwei um $90^\circ$ verdrehte Zahlenstränge für Real– und Imaginärteil aufgespannt wird.
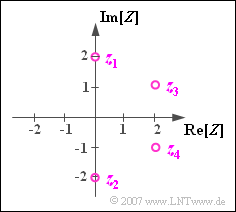
$\text{Beispiel 1:}$ Die komplexe Zahl $z_1 = 2 \cdot {\rm j}$ ist eine der zwei möglichen Lösungen der Gleichung $z^2+4=0$. Die andere Lösung ist $z_2 = -2 \cdot {\rm j}$.
Dagegen geben $z_3 = 2 + {\rm j}$ und $z_4 = 2 -{\rm j}$ die beiden Lösungen zu folgender Gleichung an:
- $$(z-2- {\rm j})(z-2+ {\rm j}) = 0 \; \ \Rightarrow \;\ z^{2}-4 \cdot z+5=0.$$
Man bezeichnet $z_4 = z_3^\ast$ auch als die Konjugiert-Komplexe von $z_3$.
- Die Summe $z_3 + z_4$ ist rein reell:
- $$z_3 + z_4 = 2 \cdot {\rm Re}[z_3]=2 \cdot {\rm Re}[z_4].$$
- Die Differenz $z_3 - z_4$ ist rein imaginär:
- $$z_3 - z_4 = {\rm j} \cdot \big [2 \cdot {\rm Im}[z_3] \big ] ={\rm j} \cdot \big [-2 \cdot {\rm Im}[z_4] \big ].$$
Anmerkung: In der Literatur werden komplexe Größen oft durch Unterstreichung gekennzeichnet. Hierauf wird in den $\rm LNTwww$–Büchern verzichtet.
Darstellung nach Betrag und Phase
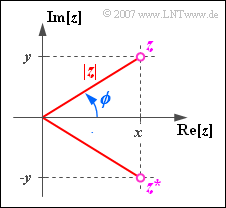
Eine komplexe Zahl $z$ kann außer durch den Realteil $x$ und den Imaginärteil $y$ auch durch ihren Betrag $|z|$ und die Phase $\phi$ beschrieben werden.
Es gelten folgende Umrechnungen:
- $$\left | z \right | = \sqrt{x^{2}+y^{2}}, \hspace{0.6cm}\phi = \arctan ({y}/{x}),$$
- $$x = |z| \cdot \cos(\phi), \hspace{0.6cm} y = |z| \cdot \sin(\phi ).$$
Somit kann die komplexe Größe $z$ auch in folgender Form dargestellt werden:
- $$z = |z| \cdot \cos (\phi) + {\rm j} \cdot |z| \cdot \sin (\phi) = |z| \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi}.$$
Hierbei wurde der Satz von Euler verwendet, der unten bewiesen wird. Dieser besagt, dass die komplexe Größe $ {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi}$ den Realteil $\cos(\phi)$ und den Imaginärteil $\sin(\phi)$ aufweist.
Weiter erkennt man aus der Grafik, dass für die Konjugiert-Komplexe von $z = x + {\rm j}\cdot y$ gilt:
- $$z^{\star} = x - {\rm j} \cdot y = |z| \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi}.$$
$\text{Beweis des Eulerschen Satzes:}$ Dieser basiert auf dem Vergleich von Potenzreihenentwicklungen.
- Die Reihenentwicklung der Exponentialfunktion lautet:
- $${\rm e}^{x} = 1 + \frac{x}{1!}+ \frac{x^2}{2!}+ \frac{x^3}{3!} + \frac{x^4}{4!} +\text{ ...} \hspace{0.15cm}.$$
- Mit imaginärem Argument kann hierfür auch geschrieben werden:
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = 1 + {\rm j} \cdot \frac{x}{1!}+ {\rm j}^2 \cdot \frac{x^2}{2!}+ {\rm j}^3 \cdot \frac{x^3}{3!} + {\rm j}^4 \cdot \frac{x^4}{4!} + \text{ ...} \hspace{0.15cm}.$$
- Berücksichtigt man \({\rm j}^{2}=-1, \ \ {\rm j}^{3} = -{\rm j},\ \ {\rm j}^{4} = 1, \ \ {\rm j}^{5} = {\rm j}, \text{ ...} \hspace{0.15cm}\) und fasst die reellen und die imaginären Terme zusammen, so erhält man
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = A(x) + {\rm j}\cdot B(x).$$
- Für die beiden Reihen gilt dabei:
- $$A(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!}+ \text{ ...} \hspace{0.1cm}= \cos(x),\hspace{0.5cm} B(x) = \frac{x}{1!}- \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!}+ \text{ ...}= \sin(x).$$
- Daraus folgt direkt der Satz von Euler:
- $${\rm e}^{ {\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}x} = \cos (x) + {\rm j} \cdot \sin (x) \hspace{2cm} \rm q.e.d.$$
Rechenregeln für komplexe Zahlen
Die Rechengesetze für zwei komplexe Zahlen
- $$z_1 = x_1 + {\rm j} \cdot y_1 = |z_1| \cdot {\rm e}^{{\rm j}\hspace {0.05cm}\cdot \hspace {0.05cm} \phi_1}, \hspace{0.5cm} z_2 = x_2 + {\rm j} \cdot y_2 = |z_2| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_2}$$
sind derart definiert, dass sich für den Sonderfall eines verschwindenden Imaginärteils die Rechenregeln der reellen Zahlen ergeben. Man spricht vom so genannten Permanenzprinzip.
Für die Grundrechenarten gelten folgende Regeln:
- Die Summe zweier komplexer Zahlen (bzw. deren Differenz) wird gebildet, indem man ihre Real- und Imaginärteile addiert (bzw. subtrahiert):
- \[z_3 = z_1 + z_2 = (x_1+x_2) + {\rm j}\cdot (y_1 + y_2),\]
- \[z_4 = z_1 - z_2 = (x_1-x_2) + {\rm j}\cdot (y_1 - y_2).\]
- Das Produkt zweier komplexer Zahlen kann in der Realteil- und Imaginärteildarstellung durch Ausmultiplizieren unter Berücksichtigung von \({\rm j}^{2}=-1\) gebildet werden. Einfacher gestaltet sich die Multiplikation allerdings, wenn \(z_1\) und \(z_2\) mit Betrag und Phase geschrieben werden:
- \[z_5 = z_1 \cdot z_2 = (x_1\cdot x_2 - y_1\cdot y_2) + {\rm j}\cdot (x_1\cdot y_2 + x_2\cdot y_1),\]
- \[z_5 = |z_1| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_1} \cdot |z_2| \cdot {\rm e}^{{\rm j}\hspace {0.05cm}\cdot \hspace {0.05cm} \phi_2}= |z_5| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_5} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |z_5| = |z_1| \cdot |z_2| , \hspace{0.3cm}\phi_5 = \phi_1 + \phi_2 .\]
- Die Division ist in der Exponentialschreibweise ebenfalls überschaubarer. Die beiden Beträge werden dividiert und die Phasen im Exponenten subtrahiert:
- \[z_6 = \frac{z_1}{z_2} = |z_6| \cdot {\rm e}^{{\rm j} \hspace {0.05cm}\cdot \hspace {0.05cm} \phi_6} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |z_6| = \frac{|z_1|}{|z_2|}, \hspace{0.3cm}\phi_6 = \phi_1 - \phi_2 .\]
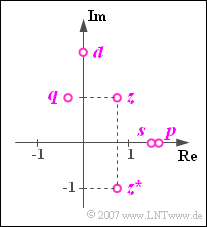
$\text{Beispiel 2:}$ In der Grafik sind als Punkte innerhalb der komplexen Ebene dargestellt:
- die komplexe Zahl \(z=0.75 + {\rm j} = 1.25 \cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.03cm} \cdot \hspace{0.05cm}53.1^{\circ} }\),
- deren Konjugiert-Komplexe \(z^{\ast} = 0.75 - {\rm j} = 1.25 \cdot {\rm e}^{ - {\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}53.1^{\circ} }\),
- die Summe \(s=z+z^{\ast}=1.5\) (rein reell),
- die Differenz \(d=z-z^{\ast}=2 \cdot {\rm j}\) (rein imaginär),
- das Produkt \(p=z \cdot z^{\ast} = 1.25^{2} \approx 1.5625\) (ebenfalls rein reell),
- der Quotient \(q= {z}/{z^{\ast} }={\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}106.2^{\circ} }\) mit Betrag $1$ und dem doppelten Phasenwinkel von $z$.
Die Thematik dieses Kapitels wird ausführlich im Lernvideo Rechnen mit komplexen Zahlen behandelt.
Aufgaben zum Kapitel
Aufgabe 1.3: Rechnen mit komplexen Zahlen
Aufgabe 1.3Z: Nochmals komplexe Zahlen