Signaldarstellung/Fast-Fouriertransformation (FFT): Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
:$$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$ | :$$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$ | ||
| − | gemäß den in Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation (DFT)]] angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die DFT, also die Berechnung der $D(\mu)$ aus den $d(\nu)$: | + | gemäß den in Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation (DFT)]] angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die DFT, also die Berechnung der $D(\mu)$ aus den $d(\nu)$: |
:$$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} | :$$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} | ||
| Zeile 19: | Zeile 19: | ||
d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}$$ | d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}$$ | ||
| − | Der hierfür erforderliche Rechenaufwand soll | + | Der hierfür erforderliche Rechenaufwand soll abgeschätzt werden, wobei wir davon ausgehen, dass die Potenzen des komplexen Drehfaktors $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ bereits in Real– und Imaginärteilform in einer Lookup–Tabelle vorliegen. Zur Berechnung eines einzelnen Koeffizienten benötigt man dann $N-1$ komplexe Multiplikationen und ebenso viele komplexe Additionen, wobei zu beachten ist: |
*Jede komplexe Addition erfordert zwei reelle Additionen: | *Jede komplexe Addition erfordert zwei reelle Additionen: | ||
:$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | :$$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + | ||
| Zeile 27: | Zeile 27: | ||
R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot | ||
I_1)\hspace{0.05cm}.$$ | I_1)\hspace{0.05cm}.$$ | ||
| − | *Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich: | + | *Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich: |
:$$M = 4 \cdot N \cdot (N-1),$$ | :$$M = 4 \cdot N \cdot (N-1),$$ | ||
:$$A = 2 \cdot N \cdot | :$$A = 2 \cdot N \cdot | ||
(N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$ | (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$ | ||
| − | *In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten: | + | *In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten: |
:$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$ | :$$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
| − | *Man benötigt bereits für eine ''Diskrete Fouriertransformation'' (DFT) mit $N = 1000$ knapp acht Millionen Rechenoperationen. | + | *Man benötigt bereits für eine ''Diskrete Fouriertransformation'' (DFT) mit $N = 1000$ knapp acht Millionen Rechenoperationen. Gleiches gilt für eine IDFT. |
| − | + | *Mit $N =16 $ sind immerhin noch $1920$ Rechenoperationen erforderlich.}} | |
| − | *Mit $N =16 $ sind immerhin noch 1920 Rechenoperationen erforderlich.}} | ||
| − | Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Sammelbegriff '''Fast–Fouriertransformation''' – abgekürzt FFT – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT. | + | Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Sammelbegriff '''Fast–Fouriertransformation''' – abgekürzt '''FFT''' – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT. |
==Überlagerungssatz der DFT== | ==Überlagerungssatz der DFT== | ||
<br> | <br> | ||
| − | Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$. Dargestellt ist hier der Übergang vom Zeit– in den Spektralbereich, also die Berechnung der Spektralbereichskoeffizienten aus den Zeitbereichskoeffizienten: | + | Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$. Dargestellt ist hier der Übergang vom Zeit– in den Spektralbereich, also die Berechnung der Spektralbereichskoeffizienten aus den Zeitbereichskoeffizienten: $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle.$ |
[[Datei:P_ID1170__Sig_T_5_5_S2_v2.png|center|frame|Überlagerungssatz der DFT]] | [[Datei:P_ID1170__Sig_T_5_5_S2_v2.png|center|frame|Überlagerungssatz der DFT]] | ||
Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet: | Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet: | ||
| − | *Die Folge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente | + | *Die Folge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente |
:$$d_1(\nu) = d(2\nu), $$ | :$$d_1(\nu) = d(2\nu), $$ | ||
:$$d_2(\nu) = d(2\nu+1) | :$$d_2(\nu) = d(2\nu+1) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Die Ausgangsfolgen $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$: | + | *Die Ausgangsfolgen $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$: |
:$$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$ | :$$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$ | ||
:$$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$ | :$$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$ | ||
| − | *Die Ausgangswerte $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$ der unteren (grünen) DFT (mit $0 \le \mu \lt N/2$ | + | *Die Ausgangswerte $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$ der unteren (grünen) DFT $($mit $0 \le \mu \lt N/2)$ werden danach im rot umrandeten Block durch komplexe Drehfaktoren hinsichtlich der Phasenlage verändert: |
:$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = | :$$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = | ||
{\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$ | {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$ | ||
| − | *Jeder einzelne '''Butterfly''' im blau umrandeten Block (in der Grafikmitte) liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei: | + | *Jeder einzelne '''Butterfly''' im blau umrandeten Block (in der Grafikmitte) liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei: |
:$$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$ | :$$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$ | ||
:$$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$ | :$$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$ | ||
| − | + | Durch '''diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand'''. | |
| − | Durch '''diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand'''. | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der | + | Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der '''Zeile 2''' der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$ ausgedrückt wird. |
| − | Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der | + | Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der '''Zeile 3''' angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$ sein. |
| − | [[Datei:Sig_T_5_5_S2b_Version2.png|center|frame|Ergebnistabelle zum Beispiel 1 zum Überlagerungssatz der DFT]] | + | [[Datei:Sig_T_5_5_S2b_Version2.png|center|frame|Ergebnistabelle zum $\text{Beispiel 1}$ zum Überlagerungssatz der DFT]] |
| − | Spaltet man die Gesamtfolge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ in zwei Teilfolgen $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {d_2}'(\nu)\hspace{0.1cm}\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten $(\nu = 0, 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm}, N–2)$ und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten $(\nu = 1, 3, \hspace{0.03cm}\text{ ...} \hspace{0.1cm} , N–1)$ beinhalten und alle anderen zu Null gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich: | + | Spaltet man die Gesamtfolge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ in zwei Teilfolgen $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {d_2}'(\nu)\hspace{0.1cm}\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten $(\nu = 0, 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm}, N–2)$ und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten $(\nu = 1, 3, \hspace{0.03cm}\text{ ...} \hspace{0.1cm} , N–1)$ beinhalten und alle anderen zu Null gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich: |
:$$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$ | :$$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$ | ||
:$$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$ | :$$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$ | ||
| − | In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man: | + | In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man: |
| − | *Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch $D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu )$. Dies lässt sich zum Beispiel mit dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Multiplikation_mit_Faktor_-_Additionssatz|Additionstheorem linearer Systeme]] begründen. | + | *Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch $D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu )$. Dies lässt sich zum Beispiel mit dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Multiplikation_mit_Faktor_-_Additionssatz|Additionstheorem linearer Systeme]] begründen. |
| − | *Die Periode der Folge $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ | + | *Die Periode der Folge $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ ist aufgrund des Nullsetzens eines jeden zweiten Zeitkoeffizienten nun $N/2$ im Gegensatz zur Periode $N$ der Folge $\langle \hspace{0.1cm} D(\mu )\hspace{0.1cm}\rangle$: |
:$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$ | :$${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$ | ||
| − | * $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ beinhaltet zusätzlich einen Phasenfaktor (Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt: | + | * $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ beinhaltet zusätzlich einen Phasenfaktor (Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt: |
:$${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$ | :$${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$ | ||
| − | *Die Berechnung von $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ ist aber jeweils ebenso aufwändig wie die Bestimmung von $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$ , da $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn einige Null sind.}} | + | *Die Berechnung von $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ ist aber jeweils ebenso aufwändig wie die Bestimmung von $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$, da $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn einige Null sind.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
| − | Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen $8$ bis $12$ erweitert. | + | Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen $8$ bis $12$ erweitert. |
| − | [[Datei:Sig_T_5_5_S2c_Version2.png|center|frame|Ergebnistabelle zum Beispiel 2 zum Überlagerungssatz der DFT]] | + | [[Datei:Sig_T_5_5_S2c_Version2.png|center|frame|Ergebnistabelle zum $\text{Beispiel 2}$ zum Überlagerungssatz der DFT]] |
| − | Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$ entsprechend den Zeilen $9$ und $11$. Man erkennt: | + | Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$ entsprechend den Zeilen $9$ und $11$ . Man erkennt: |
| − | *Die | + | *Die Zeitfolgen $\langle \hspace{0.1cm}{d_1}(\nu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}(\nu )\hspace{0.1cm}\rangle$ weisen ebenso wie die dazugehörigen Spektralfolgen $\langle \hspace{0.1cm}{D_1}(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{D_2}(\mu )\hspace{0.1cm}\rangle$ nur noch die Dimension $N/2$ auf. |
| − | *Ein Vergleich der Zeilen $5$, $7$, $10$ und $12$ zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang: | + | *Ein Vergleich der Zeilen $5$, $7$, $10$ und $12$ zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang: |
:$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$ | :$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$ | ||
:$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$ | :$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$ | ||
| − | *Entsprechend | + | *Entsprechend ergibt sich für $N/2 \le \mu \lt N$: |
:$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$ | :$${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$ | ||
:$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu} | :$$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu} | ||
| Zeile 107: | Zeile 104: | ||
$$ | $$ | ||
| − | *Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{ – {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$: | + | *Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{ – {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$: |
:$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | :$${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} | ||
{D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} | {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} | ||
| Zeile 121: | Zeile 118: | ||
$\text{Fazit:}$ | $\text{Fazit:}$ | ||
*Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand. | *Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand. | ||
| − | *Statt $\mathcal{O}= 1920$ benötigt man nur noch $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen. | + | *Statt $\mathcal{O}= 1920$ benötigt man nur noch $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen. |
| − | *Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$. | + | *Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$. |
| − | *Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.}} | + | *Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.}} |
==Radix-2-Algorithmus nach Cooley und Tukey== | ==Radix-2-Algorithmus nach Cooley und Tukey== | ||
Version vom 16. Oktober 2019, 08:38 Uhr
Inhaltsverzeichnis
Rechenaufwand von DFT bzw. IDFT
Ein Nachteil der direkten Berechnung der (im Allgemeinen komplexen) DFT–Zahlenfolgen
- $$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d(\nu)\hspace{0.1cm} \rangle$$
gemäß den in Kapitel Diskrete Fouriertransformation (DFT) angegebenen Gleichungen ist der große Rechenaufwand. Wir betrachten als Beispiel die DFT, also die Berechnung der $D(\mu)$ aus den $d(\nu)$:
- $$N \cdot D(\mu) = \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} = d(0) \cdot w^{\hspace{0.03cm}0} + d(1) \cdot w^{\hspace{0.03cm}\mu}+ d(2) \cdot w^{\hspace{0.03cm}2\mu}+\hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ d(N-1) \cdot w^{\hspace{0.03cm}(N-1)\cdot \mu}$$
Der hierfür erforderliche Rechenaufwand soll abgeschätzt werden, wobei wir davon ausgehen, dass die Potenzen des komplexen Drehfaktors $w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N}$ bereits in Real– und Imaginärteilform in einer Lookup–Tabelle vorliegen. Zur Berechnung eines einzelnen Koeffizienten benötigt man dann $N-1$ komplexe Multiplikationen und ebenso viele komplexe Additionen, wobei zu beachten ist:
- Jede komplexe Addition erfordert zwei reelle Additionen:
- $$(R_1 + {\rm j} \cdot I_1) + (R_2 + {\rm j} \cdot I_2) = (R_1 + R_2) + {\rm j} \cdot (I_1 + I_2)\hspace{0.05cm}.$$
- Jede komplexe Multiplikation erfordert vier reelle Multiplikationen und zwei reelle Additionen (eine Subtraktion wird wie eine Addition behandelt):
- $$(R_1 + {\rm j} \cdot I_1) (R_2 + {\rm j} \cdot I_2) = (R_1 \cdot R_2 - I_1 \cdot I_2) + {\rm j} \cdot (R_1 \cdot I_2 + R_2 \cdot I_1)\hspace{0.05cm}.$$
- Somit sind zur Berechnung aller $N$ Koeffizienten insgesamt die folgende Anzahl $M$ reeller Multiplikationen und die Anzahl $A$ reeller Additionen erforderlich:
- $$M = 4 \cdot N \cdot (N-1),$$
- $$A = 2 \cdot N \cdot (N-1)+2 \cdot N \cdot (N-1)=M \hspace{0.05cm}.$$
- In heutigen Rechnern benötigen Multiplikationen und Additionen/Subtraktionen etwa die gleiche Rechenzeit. Es genügt, die Gesamtzahl $\mathcal{O} = M + A$ aller Operationen zu betrachten:
- $$\mathcal{O} = 8 \cdot N \cdot (N-1) \approx 8 \cdot N^2\hspace{0.05cm}.$$
$\text{Fazit:}$
- Man benötigt bereits für eine Diskrete Fouriertransformation (DFT) mit $N = 1000$ knapp acht Millionen Rechenoperationen. Gleiches gilt für eine IDFT.
- Mit $N =16 $ sind immerhin noch $1920$ Rechenoperationen erforderlich.
Ist der Parameter $N$ eine Potenz zur Basis $2$, so können rechenzeitgünstigere Algorithmen angewendet werden. Die Vielzahl solcher aus der Literatur bekannten Verfahren werden unter dem Sammelbegriff Fast–Fouriertransformation – abgekürzt FFT – zusammengefasst. Alle diese Methoden basieren auf dem Überlagerungssatz der DFT.
Überlagerungssatz der DFT
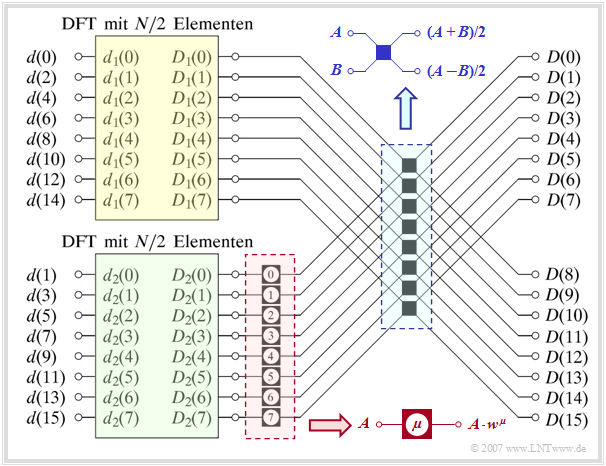
Die Grafik verdeutlicht den so genannten Überlagerungssatz der DFT am Beispiel $N = 16$. Dargestellt ist hier der Übergang vom Zeit– in den Spektralbereich, also die Berechnung der Spektralbereichskoeffizienten aus den Zeitbereichskoeffizienten: $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle.$
Der dadurch beschriebene Algorithmus ist durch folgende Schritte gekennzeichnet:
- Die Folge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ der Länge $N$ wird in zwei Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} d_2(\nu)\hspace{0.1cm}\rangle$ jeweils halber Länge separiert (in der Garafik gelb bzw. grün hinterlegt). Mit $0 \le \nu \lt N/2$ erhält man so die Folgenelemente
- $$d_1(\nu) = d(2\nu), $$
- $$d_2(\nu) = d(2\nu+1) \hspace{0.05cm}.$$
- Die Ausgangsfolgen $\langle \hspace{0.1cm}D_1(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}D_2(\mu )\hspace{0.1cm}\rangle$ der beiden Teilblöcke ergeben sich daraus jeweils durch eine eigene DFT, aber nun nur noch mit halber Länge $N/2 = 8$:
- $$\langle \hspace{0.1cm}D_1(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_1(\nu) \hspace{0.1cm}\rangle , $$
- $$ \langle \hspace{0.1cm}D_2(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N/2)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm}d_2(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$
- Die Ausgangswerte $\langle \hspace{0.1cm} D_2(\mu )\hspace{0.1cm}\rangle$ der unteren (grünen) DFT $($mit $0 \le \mu \lt N/2)$ werden danach im rot umrandeten Block durch komplexe Drehfaktoren hinsichtlich der Phasenlage verändert:
- $$D_2(\mu) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}, \hspace{0.2cm}{\rm wobei}\hspace{0.1cm}w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi/N} \hspace{0.05cm}.$$
- Jeder einzelne Butterfly im blau umrandeten Block (in der Grafikmitte) liefert durch Addition bzw. Subtraktion zwei Elemente der gesuchten Ausgangsfolge. Mit $0 \le \mu \lt N/2$ gilt dabei:
- $$D(\mu) = {1}/{2}\cdot \big[D_1(\mu) + D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big],$$
- $$D(\mu +{N}/{2}) = {1}/{2}\cdot \big[D_1(\mu) - D_2(\mu) \cdot w^{\hspace{0.04cm}\mu}\big]\hspace{0.05cm}.$$
Durch diese erste Anwendung des Überlagerungssatzes halbiert sich somit in etwa der Rechenaufwand.
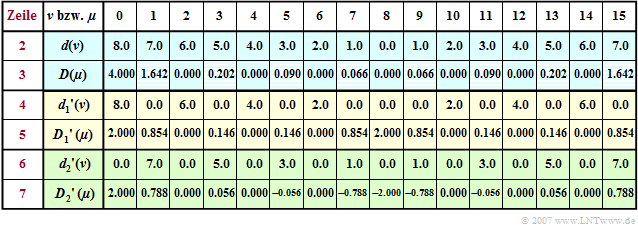
$\text{Beispiel 1:}$ Die DFT–Koeffizienten $d(\nu)$ zur Beschreibung des Zeitverlaufs seien entsprechend der Zeile 2 der folgenden Tabelle „dreieckförmig” belegt. Beachten Sie hierbei die periodische Fortsetzung der DFT, so dass der lineare Anstieg für $t \lt 0$ durch die Koeffizienten $d(8), \hspace{0.05cm}\text{ ...} \hspace{0.05cm}, d(15)$ ausgedrückt wird.
Durch Anwendung des DFT–Algorithmus mit $N = 16$ erhält man die in der Zeile 3 angegebenen Spektralkoeffizienten $D(\mu )$, die bei Vernachlässigung des Aliasingfehlers gleich $D(\mu ) = 4 \cdot \text{si}^2(\pi \cdot \mu/2)$ wären. Man erkennt, dass sich der Aliasingfehler nur auf die ungeradzahligen Koeffizienten auswirkt (schraffierte Felder). Beispielsweise müsste $D(1) = 16/ \pi^2 \approx 1.621\neq 1.642$ sein.
Spaltet man die Gesamtfolge $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle$ in zwei Teilfolgen $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {d_2}'(\nu)\hspace{0.1cm}\rangle$ auf, und zwar derart, dass die erste (gelb hinterlegte) Teilfolge nur geradzahlige Koeffizienten $(\nu = 0, 2, \hspace{0.03cm}\text{ ...} \hspace{0.1cm}, N–2)$ und die zweite (grün hinterlegt) nur ungeradzahlige Koeffizienten $(\nu = 1, 3, \hspace{0.03cm}\text{ ...} \hspace{0.1cm} , N–1)$ beinhalten und alle anderen zu Null gesetzt sind, so erhält man die zugehörigen Folgen im Spektralbereich:
- $$ \langle \hspace{0.1cm}{D_1}'(\mu)\hspace{0.1cm} \rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} {d_1}'(\nu) \hspace{0.1cm}\rangle , $$
- $$ \langle \hspace{0.1cm}{D_2}'(\mu) \hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle\hspace{0.1cm} {d_2}'(\nu) \rangle \hspace{0.1cm}\hspace{0.05cm}.$$
In den gelb bzw. grün hinterlegten Zeilen $4\hspace{0.05cm}\text{ ...} \hspace{0.05cm}7$ erkennt man:
- Wegen $d(\nu) = {d_1}'(\nu) + {d_2}'(\nu)$ gilt auch $D(\mu ) = {D_1}'(\mu ) + {D_2}'(\mu )$. Dies lässt sich zum Beispiel mit dem Additionstheorem linearer Systeme begründen.
- Die Periode der Folge $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ ist aufgrund des Nullsetzens eines jeden zweiten Zeitkoeffizienten nun $N/2$ im Gegensatz zur Periode $N$ der Folge $\langle \hspace{0.1cm} D(\mu )\hspace{0.1cm}\rangle$:
- $${D_1}'(\mu + {N}/{2}) ={D_1}'(\mu)\hspace{0.05cm}.$$
- $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ beinhaltet zusätzlich einen Phasenfaktor (Verschiebung um einen Abtastwert), der einen Vorzeichenwechsel zweier um $N/2$ auseinanderliegender Koeffizienten bewirkt:
- $${D_2}'(\mu + {N}/{2}) = - {D_2}'(\mu)\hspace{0.05cm}.$$
- Die Berechnung von $\langle \hspace{0.1cm}{D_1}'(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm} {D_2}'(\mu )\hspace{0.1cm}\rangle$ ist aber jeweils ebenso aufwändig wie die Bestimmung von $\langle \hspace{0.1cm}D(\mu )\hspace{0.1cm}\rangle$, da $\langle \hspace{0.1cm}{d_1}'(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}'(\nu)\hspace{0.1cm}\rangle$ ebenfalls aus $N$ Elementen bestehen, auch wenn einige Null sind.
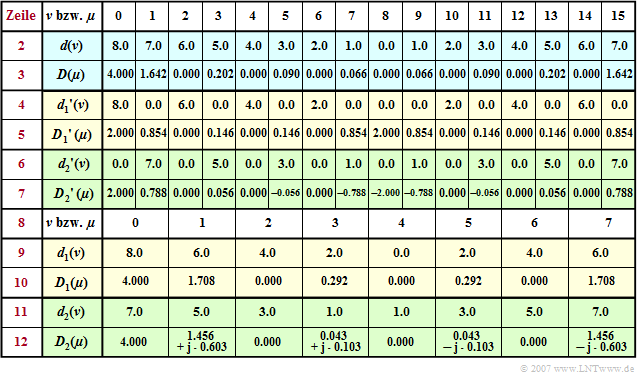
$\text{Beispiel 2:}$ Zur Fortsetzung des ersten Beispiels wird nun die bisherige Tabelle um die Zeilen $8$ bis $12$ erweitert.
Verzichtet man auf die Koeffizienten ${d_1}'(\nu) = 0$ mit ungeraden sowie auf ${d_2}'(\nu) = 0$ mit geraden Indizes, so kommt man zu den Teilfolgen $\langle \hspace{0.1cm}d_1(\nu)\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}d_2(\nu)\hspace{0.1cm}\rangle$ entsprechend den Zeilen $9$ und $11$ . Man erkennt:
- Die Zeitfolgen $\langle \hspace{0.1cm}{d_1}(\nu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{d_2}(\nu )\hspace{0.1cm}\rangle$ weisen ebenso wie die dazugehörigen Spektralfolgen $\langle \hspace{0.1cm}{D_1}(\mu )\hspace{0.1cm}\rangle$ und $\langle \hspace{0.1cm}{D_2}(\mu )\hspace{0.1cm}\rangle$ nur noch die Dimension $N/2$ auf.
- Ein Vergleich der Zeilen $5$, $7$, $10$ und $12$ zeigt für $0 \le \mu \lt N/2$ folgenden Zusammenhang:
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu)\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu)\cdot w^{\hspace{0.04cm}\mu}\hspace{0.05cm}.$$
- Entsprechend ergibt sich für $N/2 \le \mu \lt N$:
- $${D_1}'(\mu) = {1}/{2}\cdot {D_1}(\mu - {N}/{2})\hspace{0.05cm},$$
- $$ {D_2}'(\mu) = {1}/{2}\cdot {D_2}(\mu {-} {N}/{2})\cdot w^{\hspace{0.04cm}\mu} = { - } {1}/{2}\cdot {D_2}(\mu-N/2)\cdot w^{\hspace{0.04cm}\mu {-} N/2}\hspace{0.05cm}. $$
- Zum Beispiel erhält man mit $N = 16$ ⇒ $w = {\rm e}^{ – {\rm j}\hspace{0.04cm} \cdot \hspace{0.04cm}\pi/8}$ für die Indizes $\mu = 1$ bzw. $\mu = 9$:
- $${D_1}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(1) ={1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = 0.788$$
- $$\Rightarrow D(1) = {D_1}'(1)+ {D_2}'(1)= 1.642 \hspace{0.05cm}.$$
- $${D_9}'(1) = {1.708}/{2} = 0.854,\hspace{0.8cm} {D_2}'(9) = - {1}/{2}\cdot (1.456 + {\rm j} 0.603) \cdot {\rm e}^{ - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/8} = - 0.788$$
- $$\Rightarrow D(9) = {D_1}'(9)+ {D_2}'(9)= 0.066 \hspace{0.05cm}.$$
$\text{Fazit:}$
- Durch diese erste Anwendung des Überlagerungssatzes halbiert sich nahezu der Rechenaufwand.
- Statt $\mathcal{O}= 1920$ benötigt man nur noch $\mathcal{O} = 2 · 448 + 8 \cdot (4+2) + 16 \cdot 2 = 976$ reelle Operationen.
- Der erste Summand berücksichtigt die beiden DFT–Berechnungen mit $N/2 = 8$.
- Der Rest wird für die acht komplexen Multiplikationen und die $16$ komplexen Additionen bzw. Subtraktionen benötigt.
Radix-2-Algorithmus nach Cooley und Tukey
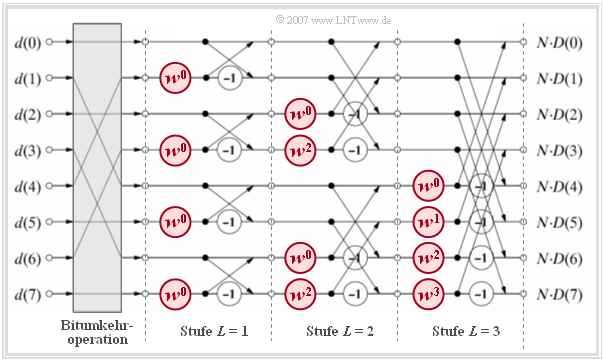
Ebenso wie andere FFT–Algorithmen baut das hier vorgestellte Verfahren [CT65][1] von James W. Cooley und John W. Tukey auf dem Überlagerungssatz der DFT auf. Es funktioniert nur dann, wenn die Stützstellenzahl $N$ eine Zweierpotenz ist.
Die Grafik verdeutlicht den Algorithmus für $N = 8$, wobei wieder die Transformation vom Zeit– in den Frequenzbereich dargestellt ist.
- Vor dem eigentlichen FFT-Algorithmus müssen zunächst die Eingangswerte $d(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, d( N - 1)$ im grauen Block „Bitumkehroperation” umsortiert werden.
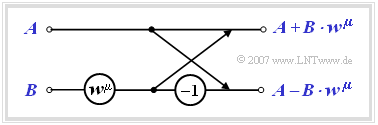
- Die Berechnung erfolgt in $\text{log}_2 N = 3$ Stufen, wobei in jeder Stufe genau $N/2 = 4$ prinzipiell gleiche Berechnungen mit verschiedenen $\mu$–Werten (= Exponent des komplexen Drehfaktors) ausgeführt werden. Eine solche Basisoperation bezeichnet man auch als Butterfly.
- Jeder Butterfly berechnet aus zwei (im Allgemeinen komplexen) Eingangsgrößen $A$ und $B$ die beiden Ausgangsgrößen $A + B \cdot w^{\mu}$ sowie $A – B \cdot w^{\mu}$ entsprechend der folgenden Skizze.
$\text{Fazit:}$ Die komplexen Spektralkoeffizienten $D(0), \hspace{0.05cm}\text{...} \hspace{0.1cm}, D( N - 1)$ erhält man am Ausgang der letzten Stufe nach Division durch $N$.
- Wie in der Aufgabe 5.5Z gezeigt wird, ergibt sich gegenüber der DFT eine deutlich kürzere Rechenzeit, zum Beispiel für $N = 1024$ um mehr als den Faktor $150$.
- Die inverse DFT zur Berechnung der Zeitkoeffizienten aus den Spektralkoeffizienten lässt sich mit dem gleichen Algorithmus und nur geringfügigen Modifizierungen bewerkstelligen.
$\text{Beispiel 3:}$
Abschließend wird ein C–Programm
- fft(N, Re, Im)
- fft(N, Re, Im)
gemäß dem oben beschriebenen Radix–2–Algorithmus angegeben:
- Beim Aufruf beinhalten die beiden Float–Arrays „Re” und „Im” die $N$ Real– und Imaginärteile der komplexen Zeitkoeffizienten $d(0)$, ... , $d( N - 1)$.
- In den gleichen Feldern „Re” und „Im” werden die $N$ komplexen Spektralkoeffizienten $D(0)$, ... , $D( N - 1)$ am Programmende an das aufrufende Programm zurückgegeben.
- Aufgrund der „In–Place”–Programmierung reichen für diesen Algorithmus $N$ komplexe Speicherplätze aus, allerdings nur, wenn zu Beginn die Eingangswerte umsortiert werden.
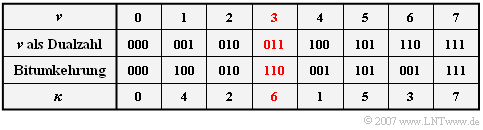
- Dies geschieht durch das Programm „bitumkehr”, wobei die Inhalte von ${\rm Re}( \nu)$ und ${\rm Im}( \nu)$ in die Elemente ${\rm Re}( \kappa)$ und ${\rm Im}( \kappa)$ eingetragen werden. $\text{Beispiel 4}$ verdeutlicht die Vorgehensweise.
$\text{Beispiel 4: Bitumkehroperation}$
- Der neue Index $\kappa$ ergibt sich, wenn man den Index $\nu$ als Dualzahl schreibt und anschließend die $\text{log}_2 \hspace{0.05cm} N$ Bits in umgekehrter Reihenfolge darstellt.
- Zum Beispiel wird aus $\nu = 3$ der neue Index $\kappa = 6$.
Aufgaben zum Kapitel
Aufgabe 5.5: Fast-Fouriertransformation
Aufgabe 5.5Z: Rechenaufwand für die FFT
Quellenverzeichnis
- ↑ Cooley, J.W.; Tukey, J.W.: An Algorithm for the Machine Calculation of Complex Fourier Series. In: Mathematics of Computation, Vol. 19, No. 90. (Apr., 1965), pp. 297-301.