Signaldarstellung/Einige Sonderfälle impulsartiger Signale: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
==Rechteckimpuls== | ==Rechteckimpuls== | ||
| − | + | <br> | |
| − | [[Datei:Sig_T_3_2_S1_version3.png|right|frame|Rechteckimpuls und Spektrum]] | + | [[Datei:Sig_T_3_2_S1_version3.png|right|frame|Rechteckimpuls und zugehöriges Spektrum]] |
Man spricht von einem '''Rechteckimpuls''', wenn für die Zeitfunktion gilt: | Man spricht von einem '''Rechteckimpuls''', wenn für die Zeitfunktion gilt: | ||
| Zeile 20: | Zeile 20: | ||
:$$X(f) = \int_{ - T/2}^{+T/2} {A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t = A }\cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$ | :$$X(f) = \int_{ - T/2}^{+T/2} {A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t = A }\cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$ | ||
| − | Hierbei berücksichtigen die Integrationsgrenzen $\pm T/2$, dass $x(t)$ ausserhalb des Intervalls von $-T/2$ bis $+T/2$ identisch | + | *Hierbei berücksichtigen die Integrationsgrenzen $\pm T/2$, dass $x(t)$ ausserhalb des Intervalls von $-T/2$ bis $+T/2$ identisch Null ist. |
| + | *Das zweite Integral verschwindet aufgrund des ungeraden Integranden und man erhält: | ||
:$$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$ | :$$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$ | ||
| Zeile 35: | Zeile 36: | ||
:$$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$ | :$$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$ | ||
| − | Wie die | + | Wie die Grafik zeigt, besitzt $X(f)$ folgende Eigenschaften: |
*Das Maximum liegt bei der Frequenz $f=0$ und hat den Wert $A \cdot T$ (Fläche des Rechtecks). | *Das Maximum liegt bei der Frequenz $f=0$ und hat den Wert $A \cdot T$ (Fläche des Rechtecks). | ||
*Bei den Frequenzen $f_n = n/T$ mit $n = ±1, ±2, ±3,\text{ ...} $ besitzt das Spektrum Nullstellen: | *Bei den Frequenzen $f_n = n/T$ mit $n = ±1, ±2, ±3,\text{ ...} $ besitzt das Spektrum Nullstellen: | ||
| Zeile 47: | Zeile 48: | ||
==Gaußimpuls== | ==Gaußimpuls== | ||
| − | + | <br> | |
Ein weiteres Beispiel eines aperiodischen Signals ist der '''Gaußimpuls''' mit dem Zeitverlauf | Ein weiteres Beispiel eines aperiodischen Signals ist der '''Gaußimpuls''' mit dem Zeitverlauf | ||
| Zeile 59: | Zeile 60: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | Als '''äquivalente Impulsdauer''' bezeichnet man allgemein die Dauer eines Rechteckimpulses mit gleicher Amplitude und Fläche wie das gegebene impulsförmige Signal $x(t)$: | |
:$$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$}} | :$$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$}} | ||
| − | Der Gaußimpuls $x(t)$ weist folgende Eigenschaften auf (siehe Grafik im Beispiel 1): | + | Der Gaußimpuls $x(t)$ weist folgende Eigenschaften auf (siehe Grafik im $\text{Beispiel 1}$): |
*Die Zeitfunktion ist für alle Zeiten von $-\infty$ bis $+\infty$ existent und positiv. | *Die Zeitfunktion ist für alle Zeiten von $-\infty$ bis $+\infty$ existent und positiv. | ||
*Das bedeutet gleichzeitig: Die absolute Impulsdauer ist unendlich groß. | *Das bedeutet gleichzeitig: Die absolute Impulsdauer ist unendlich groß. | ||
| Zeile 78: | Zeile 79: | ||
| − | [[Datei:P_ID559__Sig_T_3_2_S2_b_neu.png|right|frame|Gaußimpuls und Spektrum (Zahlenwertbeispiel)]] | + | [[Datei:P_ID559__Sig_T_3_2_S2_b_neu.png|right|frame|Gaußimpuls und zugehöriges Spektrum (Zahlenwertbeispiel)]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| Zeile 100: | Zeile 101: | ||
==Diracimpuls== | ==Diracimpuls== | ||
| − | + | <br> | |
Im Kapitel [[Signaldarstellung/Allgemeine_Beschreibung|Periodische Signale]] wurde die ''Diracfunktion'' bereits zur Beschreibung des Spektrums eines Gleichsignals oder einer harmonischen Schwingung verwendet. | Im Kapitel [[Signaldarstellung/Allgemeine_Beschreibung|Periodische Signale]] wurde die ''Diracfunktion'' bereits zur Beschreibung des Spektrums eines Gleichsignals oder einer harmonischen Schwingung verwendet. | ||
Version vom 23. Juli 2018, 17:15 Uhr
Inhaltsverzeichnis
Rechteckimpuls
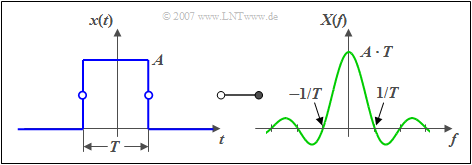
Man spricht von einem Rechteckimpuls, wenn für die Zeitfunktion gilt:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}A \\ A /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
Hierbei bezeichnet $A$ die Impulsamplitude und $T$ die Impulsdauer.
Die dazugehörige Spektralfunktion $X(f)$ erhält man durch Anwendung des ersten Fourierintegrals:
- $$X(f) = \int_{ - T/2}^{+T/2} {A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t = A }\cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$
- Hierbei berücksichtigen die Integrationsgrenzen $\pm T/2$, dass $x(t)$ ausserhalb des Intervalls von $-T/2$ bis $+T/2$ identisch Null ist.
- Das zweite Integral verschwindet aufgrund des ungeraden Integranden und man erhält:
- $$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$
$\text{Definition:}$ Zur Abkürzung definieren wir nachfolgende Funktion und bezeichnen diese als si-Funktion oder auch als Spaltfunktion:
- $${\rm si}\hspace{-0.08cm}\left( x \right) = \sin \left( x \right)/x.$$
Durch eine Erweiterung von Zähler und Nenner jeweils mit $T$ kann man für die Spektralfunktion des Rechteckimpulses auch schreiben:
- $$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right).$$
Wie die Grafik zeigt, besitzt $X(f)$ folgende Eigenschaften:
- Das Maximum liegt bei der Frequenz $f=0$ und hat den Wert $A \cdot T$ (Fläche des Rechtecks).
- Bei den Frequenzen $f_n = n/T$ mit $n = ±1, ±2, ±3,\text{ ...} $ besitzt das Spektrum Nullstellen:
- $$X( {f = f_n } ) = 0.$$
- Für das Betragsspektrum gilt folgende Schranke:
- $$\left| {X( f )} \right| \le \frac{A}{\pi \cdot \left| f \right|}.$$
Gaußimpuls
Ein weiteres Beispiel eines aperiodischen Signals ist der Gaußimpuls mit dem Zeitverlauf
- $$x(t) = A \cdot {\rm e}^{ - \pi \left( {t/\Delta t} \right)^2 } .$$
Dieser Impuls wird durch zwei Parameter beschrieben, nämlich durch
- die Impulsamplitude $A$, und
- die äquivalente Impulsdauer $\Delta t$.
$\text{Definition:}$ Als äquivalente Impulsdauer bezeichnet man allgemein die Dauer eines Rechteckimpulses mit gleicher Amplitude und Fläche wie das gegebene impulsförmige Signal $x(t)$:
- $$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$
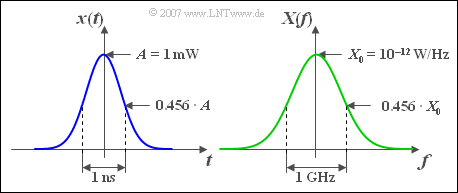
Der Gaußimpuls $x(t)$ weist folgende Eigenschaften auf (siehe Grafik im $\text{Beispiel 1}$):
- Die Zeitfunktion ist für alle Zeiten von $-\infty$ bis $+\infty$ existent und positiv.
- Das bedeutet gleichzeitig: Die absolute Impulsdauer ist unendlich groß.
- Das Impulsmaximum $A$ liegt bei $t = 0$.
- Bei $t = \pm \Delta t/2$ ist der Impuls auf $\text{e}^{-\pi/4} \approx 0.456$ des Maximums abgeklungen, und bei $t = \pm \Delta t$ ist der Signalwert kleiner als $3.5 \cdot 10^{-6} \cdot A$.
- Die Spektralfunktion $X(f)$ ist ebenfalls gaußförmig und hat sinngemäß gleiche Eigenschaften wie der gaußförmige Impuls $x(t)$:
- $$X(f) = A \cdot \Delta t \cdot {\rm e}^{ - \pi \left( {f \cdot \Delta t} \right)^2 }.$$
Auf der Seite Reziprozitätsgesetz wird auf die Analogien von Zeitbereich und Frequenzbereich des Gaußimpulses detailliert eingegangen.
Das folgende Beispiel verdeutlicht die Gemeinsamkeiten und Unterschiede zwischen dem Gaußimpuls $x(t)$ und seinem Spektrum $X(f)$.
$\text{Beispiel 1:}$ Der Ausgangsleistungsimpuls $x(t)$ eines Lasers für die digitale optische Übertragung kann im äquivalenten Tiefpassbereich mit guter Näherung als gaußförmig angenommen werden.
Die Signalparameter seien $A = 1 \,\text{mW}$, $\Delta t =1 \,\text{ns}$. Damit erhält man im Spektralbereich die vergleichbaren Kenngrößen:
- das Maximum $X_0 = X(f=0) = A \cdot \Delta t = 10^{-12} \,\text{W/Hz}$,
- die äquivalente Bandbreite $\Delta f = 1/\Delta t = 1 \,\text{GHz}$.
Theoretisch erstreckt sich das absolute Frequenzband bis ins Unendliche. Allerdings ist bei $f = 2 \cdot \Delta f = 2\,\text{GHz}$ die Spektralfunktion gegenüber ihrem Maximum schon um den Faktor $3.5 \cdot 10^{-6}$ abgeklungen.
Wir möchten Sie auf zwei interaktive Applets zu dieser Thematik aufmerksam machen, mit denen Sie sich die Zeit– und Frequenzbereichsdarstellungen von Gaußimpuls, Rechteckimpuls, Dreieckimpuls, Trapezimpuls und Cosinus–Rolloff–Impuls parametrisiert anzeigen lassen:
Ebenso ist die Darstellung der so genannten „dualen Korrespondenzen” möglich.
Diracimpuls
Im Kapitel Periodische Signale wurde die Diracfunktion bereits zur Beschreibung des Spektrums eines Gleichsignals oder einer harmonischen Schwingung verwendet.
In der Nachrichtentechnik ist es aber auch üblich und äußerst vorteilhaft, kurzfristige impulsartige Vorgänge mit Hilfe dieser mathematischen Funktion im Zeitbereich zu beschreiben und zu analysieren.
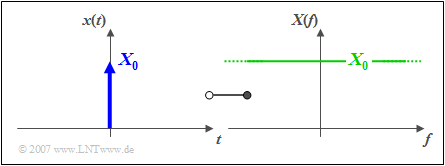
$\text{Definition:}$ Man bezeichnet als Diracimpuls den Zeitverlauf
- $$x(t) = X_0 \cdot \delta (t),$$
der wie folgt charakterisiert werden kann (siehe Skizze):
- Der Diracimpuls ist unendlich schmal ⇒ es ist $x(t)$ = 0 für $t \neq 0$ und zum Zeitpunkt $t = 0$ unendlich hoch.
- Beschreibt $x(t)$ einen Spannungsverlauf, so hat das Impulsgewicht $X_0$ die Einheit „Vs” (also die Einheit „V/Hz” einer Spektralfunktion), da $\delta (t)$ selbst die Einheit „1/s” besitzt.
- Die Spektralfunktion des Diracimpulses beinhaltet alle Frequenzen $f$ gleichermaßen: $X(f) = X_0 = \rm const.$
Die hier genannten Eigenschaften sind im folgenden Lernvideo Herleitung und Visualisierung der Diracfunktion zusammenfassend dargestellt.
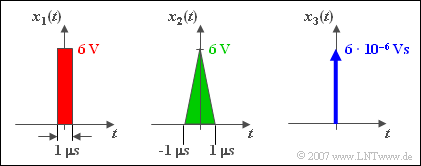
$\text{Beispiel 2:}$ Wir betrachten ein Netzwerk mit Tiefpasscharakteristik und sehr niedrigen Grenzfrequenz $f_{\rm G} = 10\,\text{ kHz}$. Dessen Ausgangssignal $y(t)$ ändert sich (nahezu) nicht, wenn eines der skizzierten Signale $x_i(t)$ an den Eingang angelegt wird.
Dieses Ergebnis kann wie folgt interpretiert werden:
- Da bei $x_1(t)$ und $x_2(t)$ die äquivalenten Impulsdauern jeweils gleich sind $(\Delta t = 1\, \mu\text{s})$ und diese sehr viel kleiner ist als $1/f_{\rm G} = 100 \, \mu\text{s}$, hat die tatsächliche Impulsform (Rechteck oder Dreieck) keinen oder nur einen untergeordneten Einfluss auf das Ausgangssignal $y(t)$.
- Beide Eingangsimpulse – sowohl das Rechteck $x_1(t)$ als auch das Dreieck $x_2(t)$ – kann man durch den Diracimpuls $x_3(t)$ annähern.
- Das Impulsgewicht $X_0 = 6 · 10^{-6}\, \text{Vs}$ muss dabei gleich den Impulsflächen von $x_1(t)$ und $x_2(t)$ sein. Voraussetzung für diese Näherung ist allerdings eine hinreichend kleine Grenzfrequenz. Bei $f_{\rm G} = 10 \, \text{MHz}$ ⇒ $1/f_{\rm G} = 100 \, \text{ns}$ wäre diese Vereinfachung dagegen nicht erlaubt.
- Auch wenn der Diracimpuls gleich hoch wie die beiden anderen Impulse gezeichnet ist, so hat er zum Zeitpunkt $t = 0$ trotzdem einen unendlich großen Wert. Beim Diracimpuls ist immer die Impulsfläche („Impulsgewicht”) angegeben. Diese unterscheidet sich gegenüber den anderen Impulsamplituden bereits in der Einheit (zum Beispiel „Vs” anstelle von „V”).
Aufgaben zum Kapitel
Aufgabe 3.3: Vom Signal zum Spektrum
Aufgabe 3.3Z: Rechteck- und Diracimpuls