Signaldarstellung/Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion: Unterschied zwischen den Versionen
Markus (Diskussion | Beiträge) |
Markus (Diskussion | Beiträge) |
||
| Zeile 12: | Zeile 12: | ||
[[Datei:P_ID735__Sig_T_4_3_S1_neu.png|Blockschaltbild eines Bandpass-Übertragungssystems]] | [[Datei:P_ID735__Sig_T_4_3_S1_neu.png|Blockschaltbild eines Bandpass-Übertragungssystems]] | ||
| − | Modulation und Demodulation sind fundamentale Komponenten eines Übertragungssystems, die im Buch Modulationsverfahren eingehend behandelt werden. Eine kurze Zusammenfassung finden Sie im Kapitel 1 des vorliegenden Buches. | + | Modulation und Demodulation sind fundamentale Komponenten eines Übertragungssystems, die im Buch [[Modulationsverfahren]] eingehend behandelt werden. Eine kurze Zusammenfassung finden Sie im Kapitel 1 des vorliegenden Buches. |
Untersuchung, Simulation, Optimierung und Dimensionierung von Bandpass-Systemen erfolgen meistens im '''äquivalenten Tiefpassbereich''', wofür folgende Gründe genannt werden können: | Untersuchung, Simulation, Optimierung und Dimensionierung von Bandpass-Systemen erfolgen meistens im '''äquivalenten Tiefpassbereich''', wofür folgende Gründe genannt werden können: | ||
| Zeile 133: | Zeile 133: | ||
Im Beispiel ist die Ortskurve eine Ellipse, die vom äquivalenten TP–Signal pro Periodendauer einmal durchlaufen wird. Die Darstellung gilt für die Zweiseitenband–Amplitudenmodulation (ZSB–AM) eines sinusförmigen 10 kHz–Signals mit einem cosinusförmigen Träger beliebiger Frequenz, wobei das obere Seitenband (blauer Zeiger) gedämpft ist. | Im Beispiel ist die Ortskurve eine Ellipse, die vom äquivalenten TP–Signal pro Periodendauer einmal durchlaufen wird. Die Darstellung gilt für die Zweiseitenband–Amplitudenmodulation (ZSB–AM) eines sinusförmigen 10 kHz–Signals mit einem cosinusförmigen Träger beliebiger Frequenz, wobei das obere Seitenband (blauer Zeiger) gedämpft ist. | ||
| − | Wären die Längen des blauen und des grünen Drehzeigers gleich, so ergäbe sich als Ortskurve eine Horizontale auf der reellen Achse – siehe Aufgabe A4.5. Im Buch | + | Wären die Längen des blauen und des grünen Drehzeigers gleich, so ergäbe sich als Ortskurve eine Horizontale auf der reellen Achse – siehe Aufgabe A4.5. Im Buch [[Modulationsverfahren]] werden die Ortskurven verschiedener Systemvarianten noch eingehend behandelt. |
| Zeile 205: | Zeile 205: | ||
Abschließend – hoffentlich nicht zu spät – wollen wir uns noch der Frage zuwenden, warum die beiden komplexen und im Verständnis komplizierteren Signale $x_+(t)$ und $x_TP(t)$ zur Beschreibung des tatsächlichen Bandpass–Signals $x(t)$ eigentlich notwendig sind. Sie wurden nicht deshalb in der Nachrichtentechnik eingeführt, um Studierende zu verunsichern, sondern: | Abschließend – hoffentlich nicht zu spät – wollen wir uns noch der Frage zuwenden, warum die beiden komplexen und im Verständnis komplizierteren Signale $x_+(t)$ und $x_TP(t)$ zur Beschreibung des tatsächlichen Bandpass–Signals $x(t)$ eigentlich notwendig sind. Sie wurden nicht deshalb in der Nachrichtentechnik eingeführt, um Studierende zu verunsichern, sondern: | ||
*Hüllkurve $a(t)$ und Phase $\Phi (t)$ können aus dem tatsächlichen, physikalischen BP–Signal $x(t)$ direkt nur in einigen Sonderfällen in einfacher Weise extrahiert werden. | *Hüllkurve $a(t)$ und Phase $\Phi (t)$ können aus dem tatsächlichen, physikalischen BP–Signal $x(t)$ direkt nur in einigen Sonderfällen in einfacher Weise extrahiert werden. | ||
| − | *Das real nicht existierende äquivalente TP–Signal $x_TP(t)$ ist ein mathematisches Hilfsmittel, mit dem die Zeitverläufe $a(t)$ und $\Phi (t)$ durch einfache geometrische Überlegungen bestimmt werden können. Im Buch | + | *Das real nicht existierende äquivalente TP–Signal $x_TP(t)$ ist ein mathematisches Hilfsmittel, mit dem die Zeitverläufe $a(t)$ und $\Phi (t)$ durch einfache geometrische Überlegungen bestimmt werden können. Im Buch [[Modulationsverfahren]] werden wir darauf zurückkommen. |
| − | *Das analytische Signal $x_+(t)$ ist ein Zwischenschritt beim Übergang von $x(t)$ zu $x_TP(t)$. Während $x_+(t)$ stets komplex ist, kann $x_TP(t)$ in Sonderfällen reell sein, zum Beispiel bei idealer Amplitudenmodulation (vergleiche Kapitel 2 des Buches | + | *Das analytische Signal $x_+(t)$ ist ein Zwischenschritt beim Übergang von $x(t)$ zu $x_TP(t)$. Während $x_+(t)$ stets komplex ist, kann $x_TP(t)$ in Sonderfällen reell sein, zum Beispiel bei idealer Amplitudenmodulation (vergleiche Kapitel 2 des Buches [[Modulationsverfahren]]). |
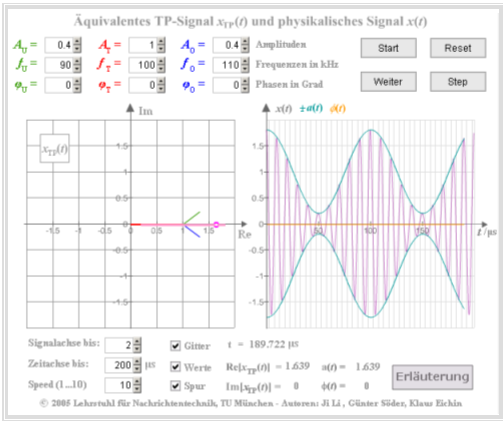
Das folgende Interaktionsmodul zeigt $x_TP(t)$ für die Summe dreier harmonischer Schwingungen: | Das folgende Interaktionsmodul zeigt $x_TP(t)$ für die Summe dreier harmonischer Schwingungen: | ||
Ortskurve – Darstellung des äquivalenten Tiefpass-Signals | Ortskurve – Darstellung des äquivalenten Tiefpass-Signals | ||
Version vom 7. Oktober 2016, 11:57 Uhr
Inhaltsverzeichnis
Motivation
Bei vielen Nachrichtenübertragungssystemen wird das niederfrequente Quellensignal $q(t)$ in ein BP–Signal $s(t)$ umgesetzt (Modulation). Nach der Übertragung muss das Empfangssignal $r(t)$ – gegenüber dem Sendesignal s(t) eventuell verzerrt und mit (Rausch-)Störungen beaufschlagt – wieder in den ursprünglichen Frequenzbereich zurückgesetzt werden (Demodulation). Das Sinkensignal $v(t)$, das möglichst gut mit $q(t)$ übereinstimmen sollte, ist wieder ein TP–Signal.
Modulation und Demodulation sind fundamentale Komponenten eines Übertragungssystems, die im Buch Modulationsverfahren eingehend behandelt werden. Eine kurze Zusammenfassung finden Sie im Kapitel 1 des vorliegenden Buches.
Untersuchung, Simulation, Optimierung und Dimensionierung von Bandpass-Systemen erfolgen meistens im äquivalenten Tiefpassbereich, wofür folgende Gründe genannt werden können:
- Sind Qualitätsmerkmale (Bandbreiteneffizienz, Signal-zu-Rauschverhältnis, Bitfehlerrate, Leistungsbedarf, usw.) eines Tiefpass-Systems bekannt, so lassen sich die entsprechenden Werte verwandter Bandpass-Systeme daraus relativ einfach herleiten. Beispiele hierfür sind die digitalen Modulationsverfahren Amplitude Shift Keying (ASK) und Binary Phase Shift Keying (BPSK), deren Performance-Größen aus dem vergleichbaren Basisbandsystem (also ohne Modulator und Demodulator) „hochgerechnet” werden können.
- Einzelne Teilkanäle bei einem sog. Frequenzmultiplexsystem, die sich durch verschiedene Trägerfrequenzen unterscheiden, können oft als qualitativ gleichwertig angesehen werden. Deshalb genügt es, die Berechnung und Dimensionierung auf einen einzigen Kanal zu beschränken und diese Untersuchungen im äquivalenten Tiefpass-Bereich – das heißt ohne Berücksichtigung der spezifischen Trägerfrequenz – durchzuführen.
- Häufig ist es so, dass die Bandbreite einer Nachrichtenverbindung um Größenordnungen kleiner ist als die Trägerfrequenz. So liegen beispielsweise beim GSM-Mobilfunk die einzelnen Kanäle im Frequenzbereich um 900 MHz (D-Netz) bzw. 1800 MHz (E-Netz), während jedem Kanal nur eine geringe Bandbreite von 200 kHz zur Verfügung steht. Deshalb ist eine Simulation im äquivalenten TP–Bereich sehr viel weniger aufwändig als eine Simulation der entsprechenden BP–Signale.
Definition im Frequenzbereich
Wir betrachten ein reelles BP–Signal $x(t)$ mit dem Spektrum $X(f)$. Weiterhin soll gelten:
- Das BP–Signal $x(t)$ sei aus der Modulation eines niederfrequenten Nachrichtensignals $q(t)$ mit dem Trägersignal $z(t)$ der Frequenz $f_T$ entstanden.
- Die Art der Modulation (ob analog oder digital, Amplituden- oder Winkelmodulation, Einseitenband oder Zweiseitenband) sei nicht festgelegt.
- Die Spektralfunktion $X_+(f)$ des dazugehörigen analytischen Signals $x_+(t)$ existiert nur für positive Frequenzen und ist hier doppelt so groß wie $X(f)$.
- Die Spektralfunktion $X_+(f)$ ist unabhängig von der Trägerfrequenz $f_T$.
Verschiebt man das Spektrum des analytischen Signals $x_+(t)$ um $f_T$ nach links, so bezeichnet man das Ergebnis als das Spektrum des äquivalenten Tiefpass-Signals:
$$X_{\rm TP}(f) = X_{\rm +}(f + f_{\rm T}).$$
Im Allgemeinen sind $X(f)$, $X_+(f)$ und $X_{TP}(f)$ komplexwertig. Ist allerdings $X(f)$ rein reell, so sind auch die Spektralfunktionen $X_+(f)$ und $X_{TP}(f)$ rein reell, weil sich diese aus $X(f)$ nur aus den Operationen „Abschneiden und Verdoppeln” bzw. „Frequenzverschiebung” ergeben.
Bei der Berechnung des äquivalenten TP–Spektrums $X_{TP}(f)$ ist – im Gegensatz zu $X_+(f)$ – die Kenntnis der Trägerfrequenz $f_T$ unbedingt erforderlich. Für andere Werte von $f_T$ ergeben sich auch andere Tiefpass–Spektren.
Transformiert man obige Gleichung in den Zeitbereich, so erhält man:
$$x_{\rm TP}(t) = x_{\rm +}(t)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}.$$
Mit der Beziehung $x(t) = \text{Re}[x_+(t)]$ ergibt sich die Vorgehensweise, wie aus dem äquivalenten TP–Signal das tatsächliche, physikalische Bandpass–Signal berechnet werden kann:
$$x(t) = {\rm Re}[x_{\rm +}(t)] = {\rm Re}[x_{\rm TP}(t)\cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2\pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t}].$$
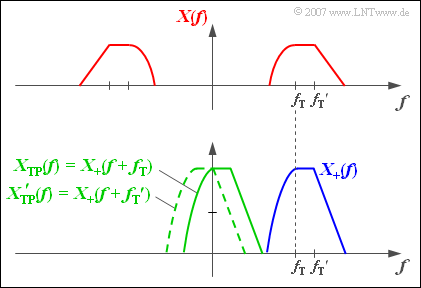
Das folgende Bild zeigt oben die rein reelle Spektralfunktion $X(f)$ eines BP–Signals $x(t)$, das aus der Modulation eines niederfrequenten Signals $q(t)$ mit der Trägerfrequenz $f_T$ entstanden sei.
Darunter dargestellt sind die beiden ebenfalls reellen Spektralfunktionen $X_+(f)$ und $X_{TP}(f)$. Aufgrund der Unsymmetrien bezüglich des Frequenzursprungs ($f$ = 0) sind die zugehörigen Zeitfunktionen komplex.
- Die durchgezogen–grün dargestellte Spektralfunktion $X_{TP}(f)$ ist gegenüber$X_{+}(f)$ um die Trägerfrequenz $f_T$ nach links verschoben.
- Wäre das Spektrum $X(f)$ aber das Modulationsergebnis eines anderen Nachrichtensignals $q'(t)$ mit einer anderen Trägerfrequenz f_T', so würde sich auch ein anderes äquivalentes TP–Signal ergeben, dessen Spektralfunktion in obiger Grafik gestrichelt eingezeichnet ist.
Beschreibung im Zeitbereich
Zur Vereinfachung der Darstellung gehen wir von einem Linienspektrum aus, so dass man das analytische Signal als Summe von komplexen Drehzeigern (als Zeigerverbund) darstellen kann:
$$X_{+}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j} \varphi_i}\cdot\delta (f - f_i) \hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{+}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}( 2 \pi f_i t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Durch die Frequenzverschiebung um $f_T$ nach links lautet somit das äquivalente TP–Signal im Frequenz– und Zeitbereich:
$$X_{\rm TP}(f) = \sum_{i=1}^{I} {A_i} \cdot {\rm e}^{-{\rm j} \varphi_i}\cdot\delta (f - \nu_i)\hspace{0.3cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.3cm} x_{\rm TP}(t) = \sum_{i=1}^{I} A_i \cdot {\rm e}^{{\rm j}( 2 \pi \nu_i t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Zwischen den Frequenzwerten $f_i$ und $v_i$ gilt folgender Zusammenhang ($i$ = 1, ... , $I$):
$$\nu_i = f_i - f_{\rm T} .$$
Diese Gleichungen können wie folgt interpretiert werden:
- Zur Zeit $t$ = 0 ist das äquivalente Tiefpass-Signal identisch mit dem analytischen Signal:
$$x_{\rm TP}(t = 0) = x_{\rm +}(t = 0)= \sum_{i=1}^{I} A_i \cdot {\rm e}^{{-\rm j}\hspace{0.05cm} \varphi_i}.$$
- Zu diesem Zeitpunkt ist der Zeigerverbund allein durch die $I$ Amplitudenparameter $A_i$ und die $I$ Phasenlagen $\phi_i$ festgelegt.
Zur Wiederholung aus dem vorherigen Kapitel 4.2: Alle Zeiger des analytischen Signals $x_+(t)$ drehen entsprechend den Frequenzen $f_i$ entgegen dem Uhrzeigersinn.
- Beim äquivalenten TP-Signal sind die Drehgeschwindigkeiten geringer. Zeiger mit $v_i$ > 0 drehen in mathematisch positiver Richtung, solche mit $v_i$ < 0 im Uhrzeigersinn.
- Ist der Frequenzparameter $v_i$ eines Zeigers gleich 0, so ruht dieser Zeiger in der komplexen Ebene entsprechend seiner Ausgangslage.
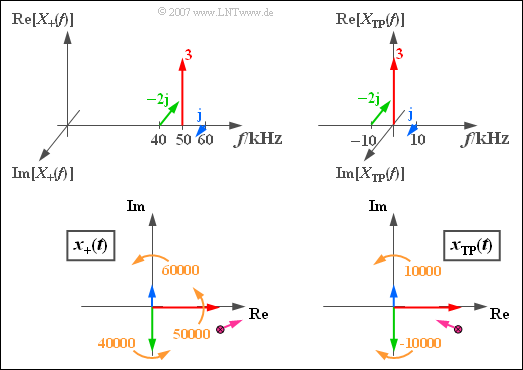
Wir betrachten ein aus drei Spektrallinien bei 40 kHz, 50 kHz und 60 kHz bestehendes Spektrum $X_+(f)$. Mit den aus der Grafik erkennbaren Amplituden– und Phasenparametern erhält man das analytische Signal $x_+(t)$ entsprechend der unteren linken Skizze.
Die Momentaufnahme der linken unteren Grafik ⇒ analytisches Signal $x_+(t)$ gilt für die Zeit $t$ = 0. Alle Zeiger drehen mit konstanter Winkelgeschwindigkeit entgegen dem Uhrzeigersinn.
- Der blaue Zeiger dreht hierbei mit 60000 Umdrehungen pro Sekunde am schnellsten und der grüne Zeiger mit der Kreisfrequenz $\omega_{40} = 2\pi \cdot 40000 1/\text{s}$ am langsamsten.
- Der violette Summenpunkt aller drei Zeiger bewegt sich für t > 0 in der komplexen Ebene in komplizierter Weise, bei obigen Zahlenwerten zuerst in die eingezeichnete Richtung.
Die rechten Grafiken beschreiben das äquivalente TP–Signal im Frequenzbereich (oben) und im Zeitbereich (unten), gültig für $f_T$ = 50 kHz.
- Der Träger liegt nun bei $f$ = 0 und der dazugehörige rote Drehzeiger bewegt sich nicht.
- Der blaue Zeiger (OSB) dreht hier mit $\omega_{10} = 2\pi \cdot 10000 1/\text{s}$ entgegen dem Uhrzeigersinn.
- Der grüne Zeiger (USB) dreht mit gleicher Geschwindigkeit entgegengesetzt ($-\omega_{10}$).
Definition der Ortskurve
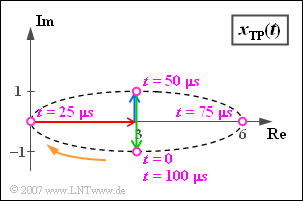 Wir betrachten das äquivalente TP–Signal $x_{TP}(t)$ des letzen Beispiels, bestehend aus
Wir betrachten das äquivalente TP–Signal $x_{TP}(t)$ des letzen Beispiels, bestehend aus
- dem ruhenden Zeiger mit der Länge 3 (rot)
- dem mit $\omega_{10} = 2\pi \cdot 10000 1/\text{s}$ in mathematisch positiver Richtung rotierenden blauen Zeiger mit der komplexen Amplitude j,
- den grünen Zeiger der Länge 2, der zum Zeitpunkt $t$ = 0 in Richtung der negativen imaginären Achse liegt. Dieser dreht sich mit gleicher Winkelgeschwindigkeit $\omega_{10}$ wie der blaue Zeiger, aber in umgekehrter Richtung ($-\omega_{10}$).
Der blaue Zeiger und der grüne Zeiger benötigen für eine Umdrehung jeweils genau eine Periodendauer $T_0$ = 100 μs. Der weitere Verlauf kann obiger Darstellung entnommen werden: Die violett eingezeichnete Zeigersumme ist zum Zeitpunkt $t$ = 0 gleich 3 – j. Nach $t$ = $T_0/4$ = 25 μs hat der resultierende Zeigerverbund den Wert 0, da nun die beiden rotierenden Zeiger in Gegenrichtung zum Träger liegen. Nach einer Periodendauer ($t$ = $T_0$ = 100 μs) ist wieder der Ausgangszustand erreicht, das heißt, es gilt $x_{TP}(t = T_0) = x_{TP}(t=0) = 3- \text{j}$.
Der Kurvenzug, auf dem sich das äquivalente Tiefpass-Signal $x_{TP}(t)$ in der komplexen Ebene bewegt, wird im Folgenden als Ortskurve bezeichnet.
Im Beispiel ist die Ortskurve eine Ellipse, die vom äquivalenten TP–Signal pro Periodendauer einmal durchlaufen wird. Die Darstellung gilt für die Zweiseitenband–Amplitudenmodulation (ZSB–AM) eines sinusförmigen 10 kHz–Signals mit einem cosinusförmigen Träger beliebiger Frequenz, wobei das obere Seitenband (blauer Zeiger) gedämpft ist.
Wären die Längen des blauen und des grünen Drehzeigers gleich, so ergäbe sich als Ortskurve eine Horizontale auf der reellen Achse – siehe Aufgabe A4.5. Im Buch Modulationsverfahren werden die Ortskurven verschiedener Systemvarianten noch eingehend behandelt.
Darstellung nach Betrag und Phase
Das äquivalente TP-Signal ist im Allgemeinen komplex und kann deshalb auch in der Form
$$x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \phi(t)}$$
dargestellt werden. Zu beachten ist das Pluszeichen im Argument der Exponentialfunktion, das sich von der kokplexen Fourierreihendarstellung unterscheidet: Man verwendet nämlich bei der Beschreibung der Modulationsverfahren auch für das physikalische Signal meist die Gleichung mit dem positiven Vorzeichen:
$$s(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)).$$
In vielen Lehrbüchern wird diese Gleichung je nach Anwendung mit Plus– oder Minuszeichen benutzt, aber stets mit gleichem Phasenbezeichner. Durch die Verwendung zweier verschiedener Symbole ($\phi$ und $\Phi$) versuchen wir in LNTwww, diese Doppeldeutigkeit zu umgehen.
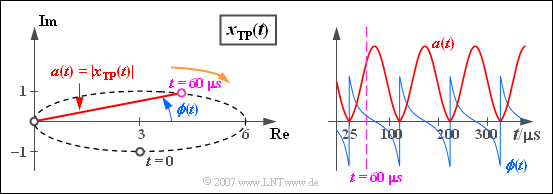
(Fortsetzung) Die Grafik bezieht sich wieder auf das Beispiel der letzten Seite.
Zu dieser Darstellung ist anzumerken: Die Betragsfunktion gibt die Zeitabhängigkeit der Zeigerlänge wieder:
$$a(t)= |x_{\rm TP}(t)|=\sqrt{{\rm Re}\left[x_{\rm TP}(t)\right]^2 + {\rm Im}\left[x_{\rm TP}(t)\right]^2 }.$$
a(t) ist wie xTP(t) periodisch mit T0 und nimmt im Beispiel Werte zwischen 0 und 6 an. Die Phasenfunktion beschreibt den zeitabhängigen Winkel des äquivalenten TP-Signals $x_{TP}(t)$, bezogen auf den Koordinatenursprung:
$$\phi(t)= {\rm arc} \left[x_{\rm TP}(t)\right]= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[x_{\rm TP}(t)\right]}{{\rm Re}\left[x_{\rm TP}(t)\right]}.$$
Hier noch einige numerische Ergebnisse für die Phasenwerte:
- Die Phase im Startzeitpunkt ist $\Phi (t = 0)$ = –arctan (1/3) ≈ –18.43° = –0.32 rad.
- Bei $t$ = 25 μs sowie zu allen äquidistanten Zeiten davon im Abstand $T_0$ = 100 μs ist $x_{TP}(t)$ = 0, so dass zu diesen Zeitpunkten die Phase $\Phi (t)$ von $-\pi /2$ auf $+\pi /2$ springt.
- Zum violett eingezeichneten Zeitpunkt $t$ = 60 μs hat die Phase einen leicht positiven Wert.
Zusammenhang zwischen äquivalenten TP- und BP-Signal
Ein BP–Signal $x(t)$, das sich aus der Modulation eines niederfrequenten Nachrichtensignals $q(t)$ mit einem Trägersignal $z(t)$ der Frequenz $f_T$ ergeben hat, kann wie folgt dargestellt werden:
$$x(t) = a(t) \cdot {\cos} ( 2 \pi f_{\rm T} t + \phi(t)) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} x_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \phi(t)}.$$
Hierbei bedeuten:
- $a(t)$ ist die zeitabhängige Amplitude, die oft als Hüllkurve bezeichnet wird. Diese ist gleich dem Betrag $|x_TP(t)|$ des äquivalenten TP–Signals.
- $\Phi(t)$ ist die zeitabhängige Phase, die ebenfalls aus dem äquivalenten TP–Signal als der Winkel zum Koordinatenursprung der komplexen Ebene ermittelt werden kann.
- Die Phase $\Phi(t)$ erkennt man im physikalischen Signal $x(t)$ an den Nulldurchgängen. Bei $\Phi(t) > 0$ tritt der Nulldurchgang in $x(t)$ früher auf als beim Trägersignal $z(t$). Dagegen bedeutet $\Phi(t) < 0$ eine Verschiebung des Nulldurchgangs auf einen späteren Zeitpunkt.
- Steckt die gesamte Information über das Nachrichtensignal in $a(t)$ und $\Phi(t)$ ist konstant, so spricht man von Amplitudenmodulation. Dagegen ist bei Phasenmodulation die Hüllkurve $a(t)$ konstant, während $\Phi(t)$ die gesamte Information über das Nachrichtensignal beinhaltet.
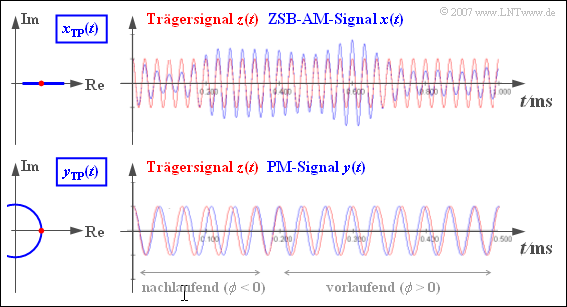
Im oberen Diagramm sehen Sie das reelle äquivalente TP–Signal $x_TP(t)$ bei ZSB–AM (Zweiseitenband–Amplitudenmodulation). Die Ortskurve ist eine horizontale Gerade, und die Nulldurchgänge des blauen ZSB–AM–Signals $x(t)$ stimmen mit denen des roten Trägersignals $z(t)$ exakt überein. Die Hüllkurve $a(t)$ beinhaltet alle Information über das Nachrichtensignal.
Die Grafik gilt für Phasenmodulation (PM). Das PM-Signal $y(t)$ hat eine konstante Einhüllende: Die Ortskurve ist ein Kreisbogen. Zu Beginn ist der Phasenwert kleiner 0, sodass die Nulldurchgänge später auftreten als beim Trägersignal $z(t)$ ⇒ „nachlaufend”. Bei positiven Werten des Nachrichtensignals gilt auch $\Phi (t) > 0$ ⇒ die Nulldurchgänge treten früher auf als beim Trägersignal ⇒ „vorlaufend”. Bei Phasenmodulation steckt also die gesamte Information über das Nachrichtensignal $q(t)$ in den Lagen der Nulldurchgänge.
Abschließend – hoffentlich nicht zu spät – wollen wir uns noch der Frage zuwenden, warum die beiden komplexen und im Verständnis komplizierteren Signale $x_+(t)$ und $x_TP(t)$ zur Beschreibung des tatsächlichen Bandpass–Signals $x(t)$ eigentlich notwendig sind. Sie wurden nicht deshalb in der Nachrichtentechnik eingeführt, um Studierende zu verunsichern, sondern:
- Hüllkurve $a(t)$ und Phase $\Phi (t)$ können aus dem tatsächlichen, physikalischen BP–Signal $x(t)$ direkt nur in einigen Sonderfällen in einfacher Weise extrahiert werden.
- Das real nicht existierende äquivalente TP–Signal $x_TP(t)$ ist ein mathematisches Hilfsmittel, mit dem die Zeitverläufe $a(t)$ und $\Phi (t)$ durch einfache geometrische Überlegungen bestimmt werden können. Im Buch Modulationsverfahren werden wir darauf zurückkommen.
- Das analytische Signal $x_+(t)$ ist ein Zwischenschritt beim Übergang von $x(t)$ zu $x_TP(t)$. Während $x_+(t)$ stets komplex ist, kann $x_TP(t)$ in Sonderfällen reell sein, zum Beispiel bei idealer Amplitudenmodulation (vergleiche Kapitel 2 des Buches Modulationsverfahren).
Das folgende Interaktionsmodul zeigt $x_TP(t)$ für die Summe dreier harmonischer Schwingungen: Ortskurve – Darstellung des äquivalenten Tiefpass-Signals
Darstellung nach Real- und Imaginärteil
Insbesondere bei der Beschreibung von Quadraturamplitudenmodulationsverfahren (QAM) eignet sich die Darstellung des äquivalenten TP–Signals nach Real– und Imaginärteil:
$$x_{\rm TP}(t) = x_{\rm I}(t)+ {\rm j} \cdot x_{\rm Q}(t).$$
In dieser Darstellung bezeichnet der Realteil $x_I(t)$ die Inphasekomponente (Normalkomponente) und der Imaginärteil $x_Q(t)$ die Quadraturkomponente von $x_TP(t)$. Mit der Betragsfunktion $a(t) = |x_{TP}(t)|$ und der Phasenfunktion $\Phi (t) = \text{arc}(x_{TP}(t))$ entsprechend den Definitionen auf den vorangegangenen Seiten gilt:
$$\begin{align*}x_{\rm I}(t) & = {\rm Re}[x_{\rm TP}(t)] = a(t) \cdot \cos (\phi(t)),\\ x_{\rm Q}(t) & = {\rm Im}[x_{\rm TP}(t)] = a(t) \cdot \sin (\phi(t)).\end{align*}$$
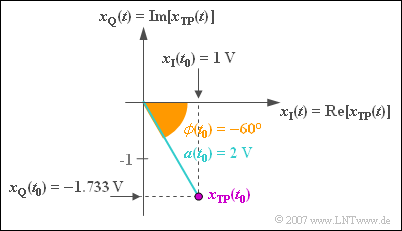
Zu einem betrachteten Zeitpunkt $t_0$ gilt für das äquivalente TP–Signal:
$$x_{\rm TP}(t = t_0) = 2\,{\rm V} \cdot {\rm e}^{-{\rm j \cdot 60 ^\circ}} = 2\,{\rm V} \cdot \cos(60 ^\circ) - {\rm j} \cdot 2\,{\rm V} \cdot \sin(60 ^\circ) = 1\,{\rm V} - {\rm j} \cdot 1.733\,{\rm V}.$$
⇒ Inphasekomponente $x_I(t = t_0) = 1\text{V}$, Quadraturkomponente $x_Q(t = t_0) = –1.733\text{V}$.
Durch Anwendung einfacher trigonometrischer Umformungen kann gezeigt werden, dass das physikalische, reelle BP–Signal auch in folgender Weise dargestellt werden kann:
$$\begin{align*}x(t) & = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi(t)) =\\ & = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )-x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ). \end{align*}$$
Das Minuszeichen ergibt sich wegen der Verwendung der Phasenfunktion $\Phi (t)$. Ein Vergleich mit der Seite Darstellung mit Cosinus- und Sinusanteil im Kapitel 2.3 zeigt, dass sich die Summe ergibt, wenn man sich auf $\phi (t) = –\Phi (t)$ bezieht. Angepasst auf unser Beispiel erhält man dann:
$$\begin{align*}x(t) & = a(t) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t - \varphi(t)) =\\ & = x_{\rm I}(t)\cdot \cos (2 \pi \cdot f_{\rm T} \cdot t )+x_{\rm Q}(t)\cdot \sin (2 \pi \cdot f_{\rm T} \cdot t ).\end{align*}$$
Die Quadraturkomponente unterscheidet sich gegenüber der oberen Gleichung im Vorzeichen.
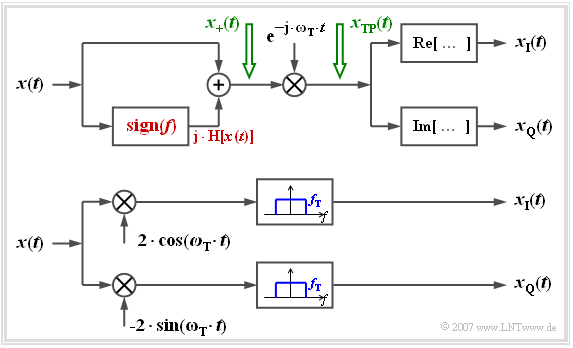
Die folgende Grafik zeigt zwei Anordnungen, um aus dem reellen Bandpass–Signal $x(t)$ das komplexe Tiefpass–Signal aufgespalten nach Inphase– und Quadraturkomponente zu ermitteln, beispielsweise zur Darstellung auf einem Oszilloskop.
Im oberen Modell wird zunächst durch Hinzufügen der Hilberttransformierten das analytische Signal $x_+(t)$ erzeugt ⇒ „Modell (B)” der verlinkten Grafik aus Kapitel 4.2. Durch Multiplikation mit der komplexen Exponentialfunktion (negativer Exponent!) kommt man zum äquivalenten Tiefpass–Signal $x_{TP}(t)$. Die gesuchten Komponenten $x_I(t)$ und $x_Q(t)$ erhält man dann durch Real– bzw. Imaginärteilbildung. Bei der unteren, der eher praxisrelevanten Anordnung erhält man für den oberen bzw. unteren Zweig nach den jeweiligen Multiplikationen:
$$\begin{align*}a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot 2 \cdot \cos (\omega_{\rm T} \cdot t ) &= a(t)\cdot \cos ( \phi(t)) + \varepsilon_{\rm oben}(t),\\ a(t)\cdot \cos (\omega_{\rm T} \cdot t + \phi(t)) \cdot (-2) \cdot \sin (\omega_{\rm T} \cdot t ) & = a(t)\cdot \sin ( \phi(t)) + \varepsilon_{\rm unten}(t)).\end{align*}$$
Die jeweils zweiten Anteile liegen um die doppelte Trägerfrequenz und werden durch die Tiefpässe mit jeweiliger Grenzfrequenz $f_T$ entfernt:
$$\begin{align*}\varepsilon_{\rm oben}(t) & = a(t)\cdot \cos (2\omega_{\rm T} \cdot t + \phi(t)),\\ \varepsilon_{\rm unten}(t) & = - a(t)\cdot \sin (2\omega_{\rm T} \cdot t + \phi(t)).\end{align*}$$
Ein Vergleich mit der letzten Seite zeigt, dass am Ausgang genau die gewünschten Komponenten $x_I(t)$ und $x_Q(t)$ abgegriffen werden können:
$$\begin{align*}x_{\rm I}(t) & = a(t)\cdot \cos ( \phi(t)) ,\\ x_{\rm Q}(t) & = a(t)\cdot \sin ( \phi(t)) .\end{align*}$$
Leistung nach Energie eines Bandpass-Signals
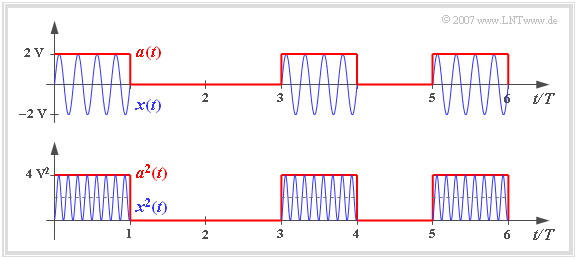
Wir betrachten das Signal $x(t)$ gemäß der Grafik, das sich zum Beispiel bei On–Off–Keying – auch bekannt als binäres Amplitude Shift Keying – ergibt. $x(t)$ ist ein BP–Signal.
Die auf $1 \Omega$ bezogene Signalleistung ergibt sich nach den Ausführungen in Kapitel 1.2 zu
$$P_x = \lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{+T_{\rm M}/2} _{-T_{\rm M}/2}\hspace{-0.1cm} x^2(t)\,{\rm d}t.$$
Sind die binären Nullen und Einsen gleichwahrscheinlich sind, so kann man auf den unendlichen Integrationsbereich und den Grenzübergang verzichten, und man erhält für obiges Mustersignal:
$$P_x = \frac{1}{2T} \cdot \int ^{2T} _{0} x^2(t)\,{\rm d}t = \frac{4\,{\rm V}^2}{2T} \cdot \int^{T} _{0} \cos^2(\omega_{\rm T} \cdot t)\,{\rm d}t= 1\,{\rm V}^2.$$
Aus der unteren Skizze ist zu erkennen, dass man durch Mittelung über die quadrierte Hüllkurve $a_2(t)$ – also über das Betragsquadrat des äquivalenten Tiefpass–Signals xTP(t) – ein um den Faktor 2 größeres Ergebnis erhält. Deshalb gilt in gleicher Weise:
$$P_x = {\frac {1}{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} |x_{\rm TP}(t)|^2\,{\rm d}t = {\frac {1}{2} \hspace{0.08cm}\cdot }\lim_{T_{\rm M} \to \infty} \frac{1}{T_{\rm M}} \cdot \int^{T_{\rm M}/2} _{-T_{\rm M}/2} a^2(t)\,{\rm d}t.$$
Dieses Resultat lässt sich verallgemeinern und es auch auf energiebegrenzte Signale anwenden. In diesem Fall gilt für die Energie entsprechend Kapitel 1.2 :
$$E_x = \int ^{+\infty} _{-\infty} x^2(t)\,{\rm d}t = {\frac {1}{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} |x_{\rm TP}(t)|^2\,{\rm d}t = {\frac {1}{2} \hspace{0.08cm}\cdot }\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t.$$
Diese Gleichung gilt allerdings nur dann exakt, wenn die zugrunde liegende Trägerfrequenz $f_T$ sehr viel größer als die BP–Bandbreite (BBP) ist.
Wir betrachten das Bandpass–Signal $x(t)$ mit $A$ = 2V, $B$ = 1 kHz und $f_T$ = 10 kHz:
$$x(t) = A \cdot {\rm si}(\pi \cdot B \cdot t) \cdot \cos(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t)),$$
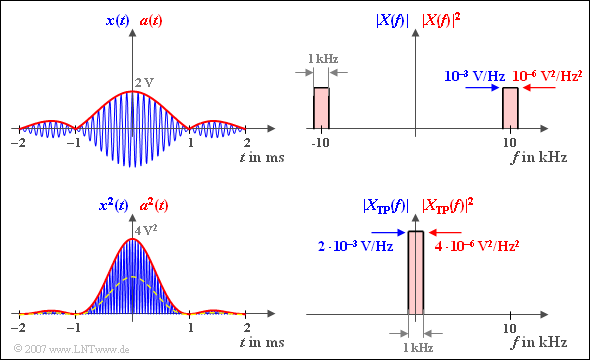 Oben dargestellt ist das Signal $x(t)$ und das in der Bandbreite $B$ konstante Betragsspektrum $|X(f)| = A/(2B) = 10^{–3}$ V/Hz. $X(f)$ setzt sich also aus zwei Rechtecken um $\pm f_T$ zusammen.
Oben dargestellt ist das Signal $x(t)$ und das in der Bandbreite $B$ konstante Betragsspektrum $|X(f)| = A/(2B) = 10^{–3}$ V/Hz. $X(f)$ setzt sich also aus zwei Rechtecken um $\pm f_T$ zusammen.
Die Energie dieses BP–Signals könnte prinzipiell nach folgender Gleichung berechnet werden:
$$E_x = \int^{+\infty} _{-\infty} A^2 \cdot \frac{{\rm sin}^2(\pi \cdot B \cdot t)}{(\pi \cdot B \cdot t)^2}\cdot \cos^2(2 \pi \cdot f_{\rm T}\cdot \hspace{0.05cm}t + \phi(t))\,{\rm d}t .$$
Entsprechend der letzten Seite gilt mit der Hüllkurve $a(t)$ von $x(t)$ aber auch:
$$\begin{align*}E_x & = {\frac {1}{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= {\frac {1}{2} \hspace{0.08cm}\cdot }\int^{+\infty} _{-\infty} |A \cdot {\rm si}(\pi \cdot B \cdot t)|^2\,{\rm d}t = \\ & = A^2\cdot \int^{+\infty} _{0} {\rm si}^2(\pi \cdot B \cdot t)\,{\rm d}t =A^2\cdot \frac {\pi}{2}\cdot \frac {1}{\pi B} = \frac {A^2}{2 B}= 2 \cdot 10^{-3}\,{\rm V}^2/{\rm Hz}.\end{align*}$$
Man erkennt, dass die Signalenergie Ex unabhängig von der Trägerphase $\Phi$ ist. Eine zweite Lösungsmöglichkeit mit gleichem Ergebnis bietet der Satz von Parseval:
$$\int ^{+\infty} _{-\infty} a^2(t)\,{\rm d}t= \int ^{+\infty} _{-\infty} |A(f)|^2\,{\rm d}f \hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_x = {1}/{2}\cdot ( {A}/{B})^2 \cdot B = {A^2}/(2 B).$$
Es gilt $|A(f)| = |X_{TP}(f)|$. Innerhalb der Bandbreite $B$ um die Frequenz $f = 0$ ist $X_{TP}(f)$ doppelt so groß wie $X(f)$ um die Frequenz $f = f_T$, nämlich $A/B$. Dies hängt mit der Definition des Spektrums $X_+(f)$ zusammen, aus dem $X_{TP}(f)$ durch Verschiebung entsteht.
Aufgaben