PN–Modulation

1. Modulationsverfahren
2. Vielfachzugriffsverfahren
3. PN–Modulation

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Blockschaltbild und äquivalentes Tiefpass–Modell

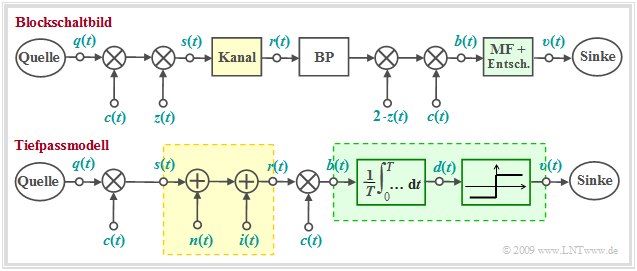
Eine Möglichkeit zur Realisierung eines CDMA–Systems bietet die so genannte PN–Modulation, die hier anhand des nachfolgend skizzierten Blockschaltbildes erklärt werden soll. Darunter gezeichnet ist das dazugehörige Modell im äquivalenten Tiefpassbereich. In beiden Bildern ist der verzerrungsfreie Kanal (AWGN und eventuell Interferenzen durch andere Nutzer) gelb hinterlegt und der optimale Empfänger (Matched–Filter plus Schwellenwertentscheider) grün.

Dieses System lässt sich wie folgt charakterisieren:

• Verzichtet man auf die Multiplikation mit dem Spreizsignal $c(t)$ bei Sender und Empfänger, so ergibt sich ein herkömmliches BPSK–System mit dem Trägersignal $z(t)$ und dem AWGN–Kanal, gekennzeichnet durch das additive Gaußsche Störsignal $n(t)$. Der zweite Störanteil (Interferenzen anderer Teilnehmer) entfällt in diesem Fall: $i(t) =$ 0.
• Für das Folgende wird vorausgesetzt (dies ist essentiell für die PN–Modulation), dass das digitale Quellensignal $q(t)$ einen NRZ–rechteckförmigen Verlauf hat. In diesem Fall lässt sich das Matched–Filter durch einen Integrator über eine Symboldauer $T$ ersetzen ⇒ Integrate & Dump. Anschließend folgt der Schwellenwertentscheider.

Prinzip und Eigenschaften von Bandspreizverfahren

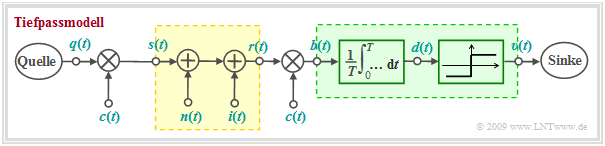
Im Folgenden betrachten wir die PN–Modulation im äquivalenten Tiefpassbereich. Charakteristisch für diese Modulationsart ist die Multiplikation des bipolaren und rechteckförmigen Digitalsignals $q(t)$ mit einer pseudozufälligen ±1–Spreizfolge $c(t)$: $$s(t) = q(t) \cdot c(t) \hspace{0.05cm}.$$ Die Dauer $T_c$ eines Spreizchips ist um den ganzzahligen Spreizfaktor $J$ kleiner ist als die Dauer $T$ eines Quellensymbols, so dass das Sendesignalspektrum $$S(f) = Q(f) \star C(f)$$ etwa um diesen Faktor $J$ breiter ist als die Spektralfunktion $Q(f)$ des Quellensignals. Deshalb bezeichnet man dieses Verfahren auch als PN–Bandspreizung, wobei „PN” für Pseudo–Noise steht. Im Englischen ist die Bezeichnung Direct Sequence Spread Spectrum, abgekürzt DS–SS, üblich.

In vorherigen Kapiteln war stets ein wesentliches Ziel der Modulation, möglichst bandbreiteneffizient zu sein. Hier versucht man im Gegensatz dazu, das Signal auf eine möglichst große Bandbreite zu spreizen.

Merke: Die Bandbreitenerweiterung um $J$ ist notwendig, um mehreren Teilnehmern die gleichzeitige Nutzung des gleichen Frequenzbandes zu ermöglichen. Im Idealfall können $2^J$ geeignete Spreizfolgen gefunden und somit ein CDMA–System für $2^J$ gleichzeitige Nutzer realisiert werden.

Desweiteren bieten Bandspreizverfahren noch folgende Vorteile:

• Man kann ein zusätzliches niederratiges DS–SS–Signal über ein ansonsten von FDMA–Kanälen höherer Datenrate genutztes Frequenzband übertragen, ohne die Hauptanwendungen signifikant zu stören. Das bandgespreizte Signal verschwindet quasi unter dem Rauschpegel dieser Signale.
• Gezielte schmalbandige Störer („Sinusstörer”) lassen sich mit dieser Technik gut bekämpfen. Dieser militärische Gesichtspunkt war auch ausschlaggebend dafür, dass Bandspreizverfahren überhaupt erfunden und weiterentwickelt wurden.
• Weiter bietet die Bandspreiztechnik allgemein, insbesondere aber Frequency Hopping (schnelle diskrete Veränderung der Trägerfrequenz über einen großen Bereich) und die Chirp–Modulation (kontinuierliches Verändern der Trägerfrequenz während eines Bitintervalls) auch die Möglichkeit, besser über frequenzselektive Kanäle übertragen zu können.

Ein Nachteil der PN–Modulation ist, dass es bei ungünstigen Bedingungen zu Interferenzen zwischen Teilnehmer kommen kann. Diese sind im Modell durch die Störgröße $i(t)$ berücksichtigt. Im Folgenden betrachten wir zunächst nur einen Sender, so dass vorerst $i(t) =$ 0 zu setzen ist.

Signalverläufe bei einem einzigen Teilnehmer (1)

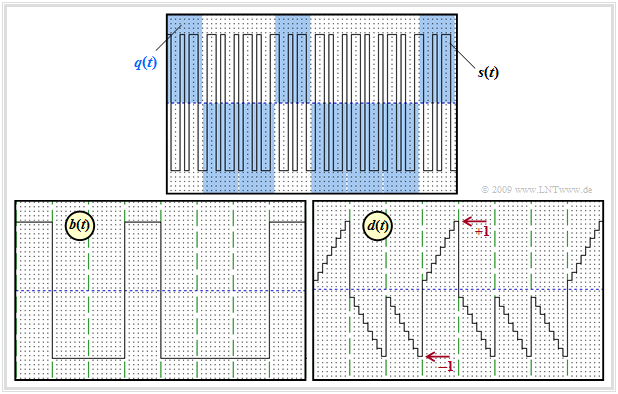
Die Grafik zeigt oben das Quellensignal $q(t)$ und das (bandgespreizte) Sendesignal $s(t)$ und unten das Signal $b(t)$ nach der Bandstauchung sowie das Detektionssignal $d(t)$ nach dem Integrator, direkt vor dem Entscheider. Es ist eine zeitdiskrete und normierte Signaldarstellung mit Rechtecken im Abstand der Chipdauer $T_c$ gewählt. Der Spreizfaktor ist $J =$ 8, als Spreizfolge wird die Walsh–Funktion Nr. 7 zugrunde gelegt. Alle Bilder gelten für den rauschfreien Fall ⇒ $n(t) =$ 0.

Zu den einzelnen Signalverläufen ist zu vermerken:

• Das ±1–Datensignal $q(t)$ ist durch die blaue Hinterlegung gekennzeichnet. Nach Multiplikation mit dem Spreizsignal $c(t)$ ergibt sich das um den Faktor $J =$ 8 höherfrequente Sendesignal $s(t)$.
• Das Spreizsignal $c(t)$ ist periodisch mit $T = J · T_c$ und besitzt somit ein Linienspektrum. Im ersten, vierten und achten Datenbit ist $c(t)$ gleich $s(t)$, zu den anderen Zeiten gilt dagegen $c(t) = \ – \ s(t)$.
• Nach der Bandstauchung, also nach chipsynchroner Multiplikation mit $c(t) ∈$ {±1} ⇒ $c^2(t) =$ 1 beim Empfänger, ergibt sich das Signal $b(t)$. Im verzerrungs– und rauschfreien Fall gilt

$$b(t) = r(t) \cdot c(t) = s(t) \cdot c(t) = \left [ q(t) \cdot c(t) \right ] \cdot c(t) = q(t) \hspace{0.05cm}.$$

• Die Integration von $b(t)$ über jeweils ein Bit ergibt ein linear ansteigendes/abfallendes Signal $d(t)$. Der Treppenverlauf im rechten Bild ist allein auf die zeitdiskrete Darstellung zurückzuführen.
• Zu den äquidistanten Detektionszeitpunkten gilt im verzerrungs– und rauschfreien Fall mit den $ν$–ten Amplitudenkoeffizienten $a_ν$ des Quellensignals $q(t)$:

$$ d (\nu T) = \frac{1}{T} \cdot \hspace{-0.3cm} \int_{(\nu -1 )T }^{\nu T}\hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t = a_\nu \in \{ +1, -1 \}\hspace{0.05cm}.$$

Signalverläufe bei einem einzigen Teilnehmer (2)

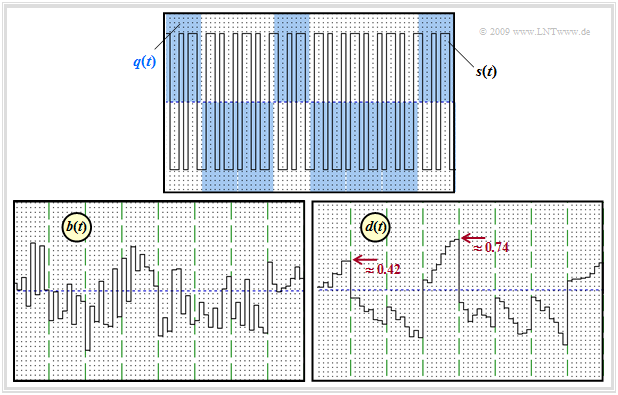
Die beiden unteren Grafiken ändern sich signifikant, wenn man AWGN–Rauschen berücksichtigt. Der AWGN–Parameter ist für diese Darstellung zu 10 · lg $(E_{\rm B}/N_0) =$ 6 dB vorausgesetzt.

Nun ist das bandgestauchte Signal $b(t)$ nicht mehr abschnittsweise konstant und das Detektionssignal $d(t)$ nicht mehr linear ansteigend bzw. abfallend. Nach Schwellenwertentscheidung der Detektionsabtastwerte $d(νT)$ ergeben sich trotzdem meist die gesuchten Amplitudenkoeffizienten, wobei sich „meist” durch die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ quantifizieren lässt. Wegen $$b(t) = \left [ s(t) + n(t) \right ] \cdot c(t) = q(t) + n(t) \cdot c(t)$$ und aufgrund der Tatsache, dass die statistischen Eigenschaften von weißem Rauschen $n(t)$ durch die Multiplikation mit dem ±1–Signal $c(t)$ nicht verändert werden, erhält man unabhängig vom Spreizgrad $J$ das gleiche Ergebnis wie bei der herkömmlichen BPSK ohne Bandspreizung und Bandstauchung: $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$

Zusätzlicher Sinusstörer um die Trägerfrequenz

Wir gehen weiterhin von nur einem einzigen Teilnehmer aus. Im Unterschied zu der Berechnung im letzten Abschnitt soll aber nun neben dem AWGN–Rauschen $n(t)$ auch ein schmalbandiger Störer $i(t)$ um die Frequenz $f_{\rm I}$ mit der Leistung $P_{\rm I}$ und der Bandbreite $B_{\rm I}$ wirksam sein.

Im Grenzfall $B_{\rm I} →$ 0 lautet das Leistungsdichtespektrum dieses „Sinusstörers”: $${\it \Phi}_{i}(f) = \frac{P_{\rm I}}{2} \cdot \left[ \delta ( f - f_{\rm I}) + \delta ( f + f_{\rm I}) \right ] \hspace{0.05cm}.$$

Bei einem herkömmlichen Übertragungssystem ohne Bandspreizung/Bandstauchung würde ein solcher Schmalbandstörer die Fehlerwahrscheinlichkeit in unzumutbarer Weise erhöhen. Bei einem System mit Bandspreizung (PN–Modulation) ist der störende Einfluss deutlich geringer, da

• die Bandstauchung beim Empfänger hinsichtlich des Sinusstörers als Bandspreizung wirkt,
• sich dadurch dessen Leistung auf ein sehr breites Frequenzband $B_c = 1/T_c >> B$ verteilt,
• die zusätzlich störende Leistungsdichte im Nutzfrequenzband $(±B)$ eher niedrig ist und durch eine geringfügige Erhöhung der AWGN–Rauschleistungsdichte $N_0$ erfasst werden kann:

$$p_{\rm B} \approx {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} +P_{\rm I} \cdot T_c} } \hspace{0.05cm} \right ) = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} } \cdot \left( \frac{1}{1+ P_{\rm I} \cdot T_c/N_0}\right ) } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$

Daraus ergibt sich die SNR–Degradation mit $T = J · T_c$ und $B = 1/T$ zu $[1 + P_{\rm I}/(J · N_0 · B)]^{–1}$. Je größer der Spreizfaktor $J$ ist, desto geringer ist die Erhöhung der Rauschleistung durch den Sinusstörer.

Diese Tatsache hat dazu geführt, dass in der Literatur der Spreizfaktor $J$ oft als Spreizgewinn bezeichnet wird, vergleiche beispielsweise [ZP85]. In diesen Büchern geht es dabei aber meist um militärische Anwendungen der Bandspreizverfahren, wobei manchmal sogar vom „günstigsten Störer” die Rede ist, nämlich dann, wenn die Degradation am größten ist. Mit solchen Anwendungen wollen wir uns hier nicht befassen.

Näherungsweise kann aber die obige Gleichung der Fehlerwahrscheinlichkeit auch angewandt werden, wenn eine ungespreizte Übertragung höherer Datenrate und ein Spread Spectrum System geringer Rate im gleichen Frequenzband arbeiten. Der störende Einfluss des erstgenannten Systems mit Bandbreite $B_{\rm I}$ auf das Spread Spectrum System lässt sich näherungsweise als Schmalbandstörer behandeln, so lange $B_{\rm I}$ hinreichend klein ist.

Beachten Sie aber bitte: Bei AWGN–Rauschen (und auch vielen anderen Kanälen) lässt sich die Bitfehlerwahrscheinlichkeit durch Bandspreizung nicht verringern. Im günstigsten Fall bleibt diese gleich (siehe letzter Abschnitt). In unserem Sinne ist Bandspreizung eine erforderliche Maßnahme, um mehrere Teilnehmer gleichzeitig im gleichen Frequenzband versorgen zu können. Wir betrachten im Folgenden ausschließlich den CDMA–Aspekt und sprechen deshalb auch weiterhin vom Spreizfaktor $J$ und nicht von einem Spreizgewinn.