Lineare zeitinvariante Systeme/Laplace–Transformation und p–Übertragungsfunktion: Unterschied zwischen den Versionen
| Zeile 36: | Zeile 36: | ||
{{Beispiel}} | {{Beispiel}} | ||
| − | Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion | + | Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion entsprechend der [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Real.E2.80.93_und_Imagin.C3.A4rteil_einer_kausalen_.C3.9Cbertragungsfunktion|Skizze]] in einem früheren Beispiel aus: |
$$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ | $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ | ||
Damit lautet die Laplace–Transformierte: | Damit lautet die Laplace–Transformierte: | ||
| − | $$X_{\rm L}(p) = \ | + | $$X_{\rm L}(p) = \int_{0}^{\infty} { {\rm e}^{-t/T}}\hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg |_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$ |
Mit $p = {\rm j} · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: | Mit $p = {\rm j} · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: | ||
$$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ | $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ | ||
Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: | Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: | ||
| − | $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0. | + | $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ |
Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_{\rm G} = 1/(2πT)$. | Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_{\rm G} = 1/(2πT)$. | ||
{{end}} | {{end}} | ||
==Einige wichtige Laplace–Korrespondenzen== | ==Einige wichtige Laplace–Korrespondenzen== | ||
| − | Unten sind einige wichtige Laplace–Korrespondenzen zusammengestellt. Die Laplace–Transformierte der Diracfunktion $δ(t)$ ist $X_{\rm L}(p) =$ | + | Unten sind einige wichtige Laplace–Korrespondenzen zusammengestellt. Die Laplace–Transformierte der [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale#Diracimpuls|Diracfunktion]] $δ(t)$ ist $X_{\rm L}(p) = 1$ (Diagramm '''A'''). Durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Integrationssatz|Integrationssatzes]] erhält man für die Sprungfunktion $X_{\rm L}(p) = 1/p$ (Diagramm '''B''') und aus dieser durch Multiplikation mit $1/(pT)$ die Laplace–Transformierte der linear ansteigenden Funktion $x(t) = t/T$ für $t > 0$ (Diagramm '''C'''). |
| − | Die Rechteckfunktion kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz]] die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt (Diagramm D). Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte (Diagramm E). | + | Die [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale#Rechteckimpuls|Rechteckfunktion]] kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatz]] die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt (Diagramm '''D'''). Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte (Diagramm '''E'''). |
| − | Die Exponentialfunktion (Diagramm F) wurde bereits auf der letzten | + | Die Exponentialfunktion (Diagramm '''F''') wurde bereits auf der [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Definition_der_Laplace.E2.80.93Transformation|letzten Seit]]e betrachtet. Mit dem Faktor $1/T$ beschreibt diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung. Durch Quadrierung erhält man die $p$–Spektralfunktion eines Tiefpasses zweiter Ordnung. Die zugehörige Zeitfunktion lautet $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm '''G'''). |
| − | Neben der kausalen si–Funktion (Diagramm H) sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion (Diagramme I und J) angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz. | + | Neben der kausalen si–Funktion (Diagramm '''H''') sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion (Diagramme '''I''' und '''J''') angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz. |
[[Datei:P_ID1758__LZI_T_3_2_S3.png | Tabelle mit einigen Laplace-Transformierten|class=fit]] | [[Datei:P_ID1758__LZI_T_3_2_S3.png | Tabelle mit einigen Laplace-Transformierten|class=fit]] | ||
Version vom 6. Februar 2017, 17:40 Uhr
Inhaltsverzeichnis
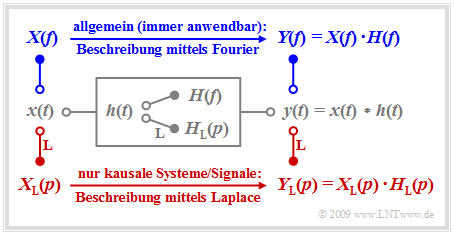
Betrachtetes Systemmodell
Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$.
Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum: $$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$ Das Fourierintegral besitzt auch für kausale Systeme und Signale, also unter der Voraussetzung $$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}$$ weiterhin Gültigkeit. In diesem Fall ergeben sich aber durch Anwendung der Laplace–Transformation unter Beachtung gewisser Restriktionen wesentliche Vorteile:
- Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten.
- Die Laplace–Transformierte $X_{\rm L}(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = {\rm j} · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit j ergibt, spielt für den Anwender keine Rolle.
- Die implizite Bedingung $x(t) = 0$ für $t < 0$ erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral.
Definition der Laplace–Transformation
Ausgehend vom ersten Fourierintegral $$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t$$ ergibt sich bei einer kausalen Zeitfunktion (wenn also gilt: $x(t) = 0$ für $t < 0$) mit der formalen Substitution $p = {\rm j} · 2πf$ direkt die Laplace–Transformation.
Die Laplace–Transformierte einer kausalen Zeitfunktion $x(t)$ lautet: $$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$
Der Zusammenhang zwischen der Laplace–Transformierten $X_{\rm L}(p)$ und dem physikalischen Spektrum $X(f)$ ist häufig wie folgt gegeben:
$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$
Beinhaltet allerdings das Signal $x(t)$ periodische Anteile und damit die Spektralfunktion $X(f)$ zusätzliche Diracfunktionen, so ist diese Gleichung nicht anwendbar. In diesem Fall muss $p = α + {\rm j} · 2πf$ angesetzt werden und es ist dann der Grenzübergang $α → 0$ zu bilden.
Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion entsprechend der Skizze in einem früheren Beispiel aus: $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ Damit lautet die Laplace–Transformierte: $$X_{\rm L}(p) = \int_{0}^{\infty} { {\rm e}^{-t/T}}\hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg |_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$ Mit $p = {\rm j} · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_{\rm G} = 1/(2πT)$.
Einige wichtige Laplace–Korrespondenzen
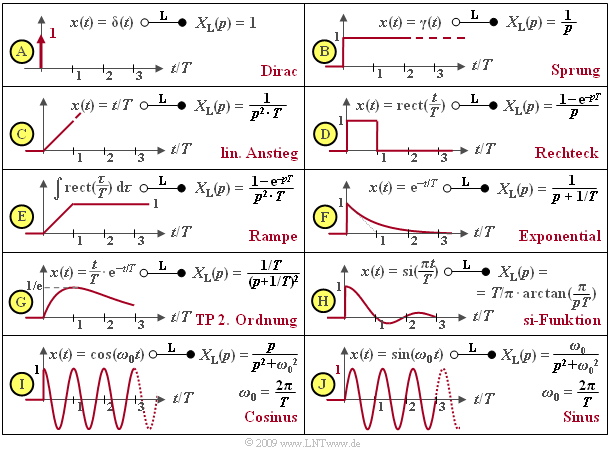
Unten sind einige wichtige Laplace–Korrespondenzen zusammengestellt. Die Laplace–Transformierte der Diracfunktion $δ(t)$ ist $X_{\rm L}(p) = 1$ (Diagramm A). Durch Anwendung des Integrationssatzes erhält man für die Sprungfunktion $X_{\rm L}(p) = 1/p$ (Diagramm B) und aus dieser durch Multiplikation mit $1/(pT)$ die Laplace–Transformierte der linear ansteigenden Funktion $x(t) = t/T$ für $t > 0$ (Diagramm C).
Die Rechteckfunktion kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem Verschiebungssatz die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt (Diagramm D). Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte (Diagramm E).
Die Exponentialfunktion (Diagramm F) wurde bereits auf der letzten Seite betrachtet. Mit dem Faktor $1/T$ beschreibt diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung. Durch Quadrierung erhält man die $p$–Spektralfunktion eines Tiefpasses zweiter Ordnung. Die zugehörige Zeitfunktion lautet $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm G).
Neben der kausalen si–Funktion (Diagramm H) sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion (Diagramme I und J) angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz.
Alle hier betrachteten Zeitsignale $x(t)$ sind dimensionslos angenommen. Aus diesem Grund besitzt $X_{\rm L}(p)$ als das Integral über die Zeit stets die Einheit „Sekunde”.
Pol–Nullstellen–Darstellung von Schaltungen
Ein jedes lineare zeitinvariante (LZI–) System, das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie Widerständen $(R)$, Kapazitäten $(C)$, Induktivitäten $(L)$ und Verstärkerelementen realisiert werden kann, besitzt eine gebrochen–rationale $p$–Übertragungsfunktion: $$H_{\rm L}(p)= \frac {A_Z \cdot p^Z + ... + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N + ... + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$
Alle Koeffizienten $A_Z, ..., A_0, B_N, ..., B_0$ sind reell. Weiter bezeichnen
- $Z$ den Grad des Zählerpolynoms $Z(p)$,
- $N$ den Grad des Nennerpolynoms $N(p)$.
Eine äquivalente Pol–Nullstellen–Darstellung der obigen Übertragungsfunktion lautet:
$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot ... \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot ... \cdot (p - p_{{\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$
Die $Z + N +$ 1 Parameter bedeuten:
- $K = A_Z/B_N$ ist ein konstanter Faktor. Gilt $Z = N$, so ist dieser dimensionslos.
- Die Lösungen der Gleichung $Z(p) =$ 0 ergeben die $Z$ Nullstellen $p_{o1}, ..., p_{oZ}$ von $H_{\rm L}(p)$.
- Die Nullstellen des Nennerpolynoms $N(p)$ liefern die $N$ Polstellen (oder kurz Pole).
Die Umformung ist eindeutig. Dies erkennt man daran, dass die obere Übertragungsfunktion ebenfalls nur durch $Z + N +$ 1 freie Parameter bestimmt ist, da einer der Koeffizienten $A_Z, ... , A_0, B_N, ... , B_0$ ohne Änderung des Quotienten auf 1 normiert werden kann.
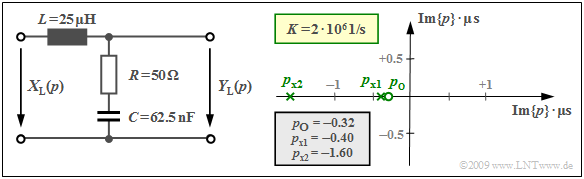
Wir betrachten den gezeichneten Vierpol mit einer Induktivität $L$ (komplexer Widerstand $pL$) im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes $R$ und einer Kapazität $C$ mit dem komplexen Widerstand $1/(pC)$.
Damit lautet die $p$–Übertragungsfunktion: $$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)}} {pL + R +{1}/{(pC)}}= \frac {1 + p \cdot{RC}} {1 + p \cdot{RC}+ p^2 \cdot{LC}} \hspace{0.05cm} .$$ Setzt man $p = {\rm j} · 2πf$ ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang). Dividiert man in obiger Gleichung Zähler und Nenner durch $LC$, so ergibt sich: $$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)}} {p^2 + {R}/ {L}\cdot p + {1}/{(LC)}}= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
Im rechten Gleichungsteil ist die Übertragungsfunktion $H_{\rm L}(p)$ in Pol–Nullstellen–Notation angegeben. Durch Koeffizientenvergleich ergeben sich für $R =$ 50 Ω. $L =$ 25 μH und $C =$ 62.5 nF folgende Werte:
- die Konstante $K = R/L = 2 · 10^6 1/{\rm s}$,
- die Nullstelle $p_o = –1/(RC) = –0.32 · 10^6 1/{\rm s},$
- die beiden Pole $p_{x1}$ und $p_{x2}$ als Lösung der Gleichung
$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC}}$$ $$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6\,\frac {1} {\rm s} \pm \sqrt{10^{12}\,\frac {1} {\rm s^2}-0.64 \cdot 10^{12}\,\frac {1} {\rm s^2}}$$ $$\Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\,{1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\, {1}/ {\rm s} \hspace{0.05cm} .$$ In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben. Die Achsen 1/μs bezeichnen den Real– und Imaginärteil der Variablen $p$, jeweils normiert auf den Wert $10^6$ · 1/s (= 1/μs). Man erkennt nach dieser Normierung die Nullstelle bei $p_o =$ –0.32 als Kreis und die beiden Polstellen bei $p_{x1} =$ –0.4 und $p_{x2} =$ –1.6 als Kreuze.
Eigenschaften der Pole und Nullstellen
Die Übertragungsfunktion $H_{\rm L}(p)$ einer jeden realisierbaren Schaltung wird durch $Z$ Nullstellen und $N$ Pole zusammen mit einer Konstanten $K$ vollständig beschrieben, wobei folgende Einschränkungen gelten:
- Es gilt stets $Z ≤ N$. Mit $Z > N$ würde sich im Grenzfall für $p → ∞$ (also für sehr hohe Frequenzen) auch eine unendlich große $p$–Übertragungsfunktion ergeben.
- Die Nullstellen $p_{oi}$ und die Pole $p_{xi}$ sind im allgemeinen komplex und weisen wie $p$ die Einheit 1/s auf. Gilt $Z < N$, so besitzt auch die Konstante $K$ eine Einheit.
- Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt. Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da $H_{\rm L}(p)$ stets eine reelle gebrochen–rationale Funktion darstellt.
- Alle Pole liegen in der linken Halbebene oder – als Grenzfall – auf der imaginären Achse. Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem Hauptsatz der Funktionstheorie, der in Kapitel 3.3 angegeben wird.
- Nullstellen können sowohl in der linken als auch in der rechten $p$–Halbebene auftreten oder auch auf der imaginären Achse. Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der Aufgabe Z3.4, die sich mit Allpässen beschäftigt.
- Bei den so genannten Minimum–Phasen–Systemen sind in der rechten $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen. Der Realteil aller Singularitäten ist hier nie positiv.
Darunterfolgend werden diese Eigenschaften an drei Beispielen verdeutlicht.
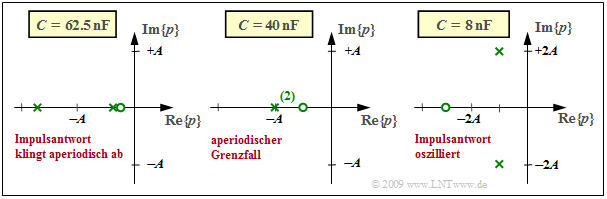
Ausgehend vom Vierpol im letzten Abschnitt $(L$ im Längszweig, $R$ und $C$ im Querzweig) können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden: $$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} \Leftarrow \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC}} \hspace{0.05cm}.$$ Die in der Grafik genannten Kapazitätswerte $C$ gelten für $R =$ 50 Ω und $L =$ 25 μH. Die Achsen sind auf die Variable $A = R/(2L) = 10^6 · 1/s$ normiert, und es gilt $K = 2A = 2 · 10^6 · 1/s.$
Die Grafik zeigt drei verschiedene Diagramme. Der konstante Faktor ist jeweils $K = 2 · 10^6 · 1/s:$
- Für $B < A$ erhält man zwei reelle Pole und eine Nullstelle rechts von $–A/2$. Beispielsweise ergibt sich für $C =$ 62.5 nF entsprechend dem linken Diagramm:
$$ {B}/ {A}= 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$
- Für $B > A$ ergeben sich zwei konjugiert–komplexe Pole und eine Nullstelle links von $–A/2$, zum Beispiel gemäß dem rechten Diagramm für $C =$ 8 nF:
$${B}/ {A}= \sqrt{5} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$
- Der Grenzfall $A = B$ führt zu einer reellen doppelten Polstelle und einer Nullstelle bei $– A/2$ (siehe mittleres Diagramm, gültig für $C =$ 40 nF):
$$ {B}/ {A}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$
Die Impulsantworten sind entsprechend dem Kapitel 3.3
- aperiodisch abklingend (linkes Diagramm),
- oszillierend (rechtes Diagramm), oder
- man spricht vom aperiodischen Grenzfall (mittleres Diagramm).
Grafische Ermittlung von Dämpfung und Phase
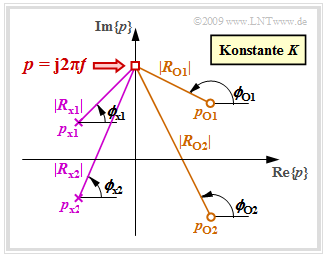
Gegeben sei die $p$–Übertragungsfunktion in der Pol–Nullstellen–Notation: $$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot ... \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot ... \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$ Zur herkömmlichen Übertragungsfunktion bzw. zum Frequenzgang $H(f)$ kömmt man, indem man das Argument $p$ der Funktion $H_{\rm L}(p)$ durch j · $2πf$ ersetzt: $$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot ... \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot ... \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$ Wir betrachten nun eine feste Frequenz $f$ und beschreiben die Abstände und Winkel aller Nullstellen durch Vektoren: $$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm exp}({\hspace{0.03cm}{\rm j}\cdot\phi_{ {\rm o} i} }), \hspace{0.3cm}i= 1, ... , Z \hspace{0.05cm} .$$ In gleicher Weise gehen wir für die Polstellen vor: $$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm exp}({\hspace{0.03cm}{\rm j}\cdot\phi_{ {\rm x} i} }), \hspace{0.3cm}i= 1, ... , N \hspace{0.05cm} .$$ Die nachfolgende Grafik zeigt die Beträge und Phasenwinkel für ein System mit $Z =$ 2 Nullstellen in der rechten Halbebene und $N =$ 2 Polstellen in der linken Halbebene. Zu berücksichtigen ist zudem die Konstante $K$.
Mit dieser Vektordarstellung kann für den Frequenzgang geschrieben werden: $$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot ... \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}... \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$ Die Bildbeschreibung wird nachfolgend fortgesetzt.
Stellt man $H(f)$ durch die Dämpfung $a(f)$ und die Phase $b(f)$ entsprechend der allgemeinen Beziehung
$$H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$$
dar, so erhält man durch den Vergleich mit der obigen Gleichung das folgende Ergebnis:
- Unter der Voraussetzung, dass alle dimensionsbehafteten Größen geeignet normiert sind, gilt für die Dämpfung in Neper (1 Np ist gleich 8.686 dB):
$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$
- Die Phasenfunktion in Radian (rad) ergibt sich entsprechend der Skizze im letzten Abschnitt zu
$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm mit} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$
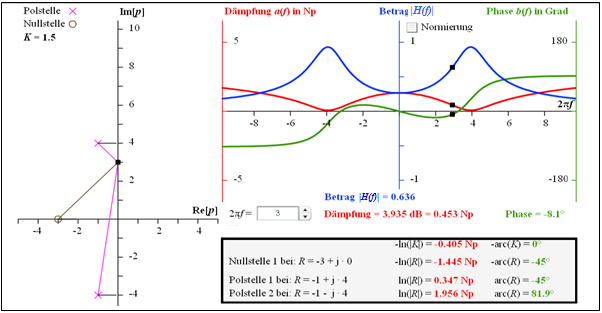
Die Grafik verdeutlicht die Berechnung der Dämpfungsfunktion $a(f)$ und der Phasenfunktion $b(f)$ eines Vierpols, der durch den Faktor $K =$ 1.5, eine Nullstelle bei –3 und zwei Pole bei –1 $±$j · 4 festliegt. Die angegebenen Zahlenwerte gelten für die Frequenz $2πf = 3$: $$a(f = \frac{3}{2\pi}) = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB} \hspace{0.2cm}\Rightarrow \hspace{0.2cm}|H(\frac{3}{2\pi})| = 0.636, b(\frac{3}{2\pi}) = -8.1 \,\,^\circ \hspace{0.05cm} .$$
Die Grafik ist ein Bildschirmabzug des Interaktionsmoduls
$$\href{https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2294&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=}{ {\rm Kausale Systeme –Laplace–Transformation} }$$
Die Dämpfung $a(f)$ ist rot dargestellt und die Phase grün. Die Herleitung dieser Zahlenwerte ist im grau hinterlegten Block verdeutlicht. Für $|H(f)|$ ergibt sich ein bandpassähnlicher Verlauf (blaue Kurve) mit $$|H(f = 0)| \approx 0.25, \hspace{0.2cm} |H(f = \frac{4}{2\pi})| \approx 0637,\hspace{0.2cm} |H(f \rightarrow \infty)|= 0 \hspace{0.05cm} .$$