Lineare zeitinvariante Systeme/Laplace–Rücktransformation: Unterschied zwischen den Versionen
| Zeile 13: | Zeile 13: | ||
[[Datei:P_ID1770__LZI_T_3_3_S1_neu.png | Voraussetzungen für Kapitel 3.3]] | [[Datei:P_ID1770__LZI_T_3_3_S1_neu.png | Voraussetzungen für Kapitel 3.3]] | ||
| + | |||
| + | $H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem, während $Y_{\rm L}(p)$ die Laplace–Transformierte des gesuchten Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ bezeichnet. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$ | ||
| + | *Die Pole und Nullstellen zeigen die in Kapitel 3.2 genannten Eigenschaften. Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind auch in der rechten $p$–Halbebene erlaubt. | ||
| + | *Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind ebenfalls erlaubt. | ||
| + | *Verwendet man ein diracförmiges Eingangssignal $x(t) = δ(t) ⇒ X_{\rm L}(p) = 1 ⇒ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt das Ausgangssignal $y(t)$ die Impulsantwort $h(t)$ des kausalen Übertragungssystems. Zur Berechnung dürfen nur die grün eingezeichneten Singularitäten herangezogen werden. | ||
| + | *Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p =$ 0 zu berücksichtigen. | ||
| + | *Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rmL}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel 3.2), zum Beispiel ein zum Zeitpunkt $t =$ 0 eingeschaltetes Cosinus– oder Sinussignal. Deren Laplace–Transformierte sind in der obigen Grafik ebenfalls angegeben. | ||
| + | |||
| + | |||
| + | Bei der hier beschriebenen Vorgehensweise ist ein Rechteck $x(t) ⇒ X_{\rm L}(p) = (1 – exp^{pT})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden. | ||
| + | |||
Version vom 12. Mai 2016, 19:40 Uhr
Problemstellung und Voraussetzungen
Das Kapitel 3.3 behandelt die folgende Problemstellung: Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. Gesucht ist die Laplace–Rücktransformierte, die die dazugehörige Zeitfunktion $y(t)$ angibt und die in diesem Tutorial wie folgt bezeichnet wird: $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$
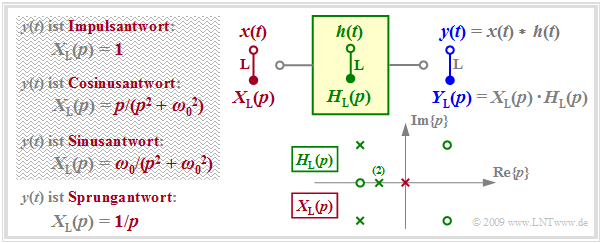
In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt:
$H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem, während $Y_{\rm L}(p)$ die Laplace–Transformierte des gesuchten Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ bezeichnet. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$
- Die Pole und Nullstellen zeigen die in Kapitel 3.2 genannten Eigenschaften. Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind auch in der rechten $p$–Halbebene erlaubt.
- Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind ebenfalls erlaubt.
- Verwendet man ein diracförmiges Eingangssignal $x(t) = δ(t) ⇒ X_{\rm L}(p) = 1 ⇒ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt das Ausgangssignal $y(t)$ die Impulsantwort $h(t)$ des kausalen Übertragungssystems. Zur Berechnung dürfen nur die grün eingezeichneten Singularitäten herangezogen werden.
- Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p =$ 0 zu berücksichtigen.
- Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rmL}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel 3.2), zum Beispiel ein zum Zeitpunkt $t =$ 0 eingeschaltetes Cosinus– oder Sinussignal. Deren Laplace–Transformierte sind in der obigen Grafik ebenfalls angegeben.
Bei der hier beschriebenen Vorgehensweise ist ein Rechteck $x(t) ⇒ X_{\rm L}(p) = (1 – exp^{pT})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden.