Erweiterungskörper

Inhaltsverzeichnis

1 GF(2²) – Beispiel eines Erweiterungskörpers (1)
2 GF(2²) – Beispiel eines Erweiterungskörpers (2)
3 GF(2²) – Beispiel eines Erweiterungskörpers (3)
4 Polynome über einem endlichen Körper (1)
5 Polynome über einem endlichen Körper (2)
6 Verallgemeinerte Definition eines Erweiterungskörpers
7 Binäre Erweiterungskörper (1)
8 Binäre Erweiterungskörper (2)
9 Binäre Erweiterungskörper (3)
10 Aufgaben

GF(2²) – Beispiel eines Erweiterungskörpers (1)

Im Kapitel 2.1 wurde bereits gezeigt, dass die endliche Zahlenmenge {0, 1, 2, 3} ⇒ q = 4 nicht die Eigenschaften eines Galoisfeldes GF(4) erfüllt. Vielmehr ergeben sich für die Addition modulo 4 und die Multiplikation modulo 4 folgende Tabellen:

\[{\rm Operationen } \hspace{0.15cm}{\rm modulo}\hspace{0.15cm}{\it q} = 4 \hspace{0.25cm} \Rightarrow\hspace{0.25cm}\]

+	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

.	1	2	3
0	0	0	0
1	1	2	3
2	2	0	2
3	3	2	1

Für z_i = 2 gibt es keine multiplikative Inverse Inv_M(z_i). Dies erkennt man daran, dass kein einziges Element z_j ∈ {0, 1, 2, 3} die Bedingung 2 · z_j = 1 erfüllt. Geht man dagegen vom binären Galoisfeld GF(2) = {0, 1} aus und erweitert dieses entsprechend der Gleichung

\[{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, \]

so ergibt sich die ebenfalls endliche Menge {0, 1, α, 1 + α} ⇒ die Ordnung ist weiterhin q = 4. Führt man die Rechenoperationen modulo p(α) = α² + α + 1 durch, so erhält man das folgende Ergebnis:

\[{\rm modulo} \hspace{0.15cm} {\it p} (\alpha) \hspace{0.25cm}\Rightarrow \]

+	0	1	α	1+α
0	0	1	α	1+α
1	1	0	1+α	α
α	α	1+α	0	1
1+α	1+α	α	1	0

.	1	α	1+α
0	0	0	0
1	1	α	1+α
α	α	1+α	1
1+α	1+α	1	α

Hierzu ist anzumerken:

Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin N_A = 0 und N_M = 1.

Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist α + α = α – α = 0. Für alle z_i gilt somit: Die additive Inverse von z_i ist das Element z_i selbst.

Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen:

\[\big [ \alpha \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + \alpha) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1\hspace{0.05cm},\]

\[\big [ \alpha \cdot \alpha \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 ) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1+\alpha\hspace{0.05cm},\]

\[\big [ (1+\alpha) \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + 1) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= \alpha\hspace{0.05cm}.\]

Damit existieren für alle Elemente mit Ausnahme des Nullelements die multiplikativen Inversen:

\[{\rm Inv_M}( 1) = 1 \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(\alpha) = 1+\alpha \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(1+\alpha) = \alpha \hspace{0.05cm}.\]

Daraus folgt: Die Menge {0, 1, α, 1 + α} stellt zusammen mit den zwei Rechenoperationen Addition und Multiplikation modulo p(α) = α² + α + 1 ein Galoisfeld der Ordnung q = 4 dar. Dieses mit GF(2²) = GF(4) bezeichnete Galoisfeld erfüllt alle in Kapitel 2.1 genannten Eigenschaften.

Im Gegensatz zum Zahlenkörper GF(3) = {0, 1, 2} mit der Eigenschaft, dass q = 3 eine Primzahl ist, nennt man GF(2²) einen Erweiterungskörper (englisch: Extension Field).

GF(2²) – Beispiel eines Erweiterungskörpers (2)

Das Polynom p(α) und damit die Bestimmungsgleichung p(α) = 0 darf nicht beliebig vorgegeben werden. Zum Beleg hierfür vergleichen wir die Verknüpfungstabellen für zwei verschiedene Polynome.

Polynom entsprechend der letzten Seite ⇒ p(α) = α² + α + 1:

+	0	1	α	1+α
0	0	1	α	1+α
1	1	0	1+α	α
α	α	1+α	0	1
1+α	1+α	α	1	0

.	1	α	1+α
0	0	0	0
1	1	α	1+α
α	α	1+α	1
1+α	1+α	1	α

Neuer (allerdings ungeeigneter) Ansatz ⇒ p(α) = α² + 1:

+	0	1	α	1+α
0	0	1	α	1+α
1	1	0	1+α	α
α	α	1+α	0	1
1+α	1+α	α	1	0

.	1	α	1+α
0	0	0	0
1	1	α	1+α
α	α	1	1+α
1+α	1+α	1+α	0

Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten:

Aus p(α) = 0 folgt nun für das Produkt α · α = 1 und das Produkt (1+α) · (1+α) ergibt das Element 0. Das gemischte Produkt α · (1+α) ist nun 1+α.

In der letzten Zeile der Multipliaktionstabelle und auch in der letzten Spalte steht nun keine „1” ⇒ Hinsichtlich der Bedingung p(α) = α² + 1 = 0 existiert die multiplikative Inverse zu 1+α nicht.

Damit erfüllt aber die endliche Menge {0, 1, α, 1+α} zusammen mit Rechenoperationen modulo p(α) = α² + 1 auch nicht die Voraussetzungen eines Erweiterungskörpers GF(2²).

Fassen wir zusammen: Aus dem binären Galoisfeld GF(2) = {0, 1} lässt sich unter Zuhilfenahme eines Polynoms vom Grad m = 2 mit binären Koeffizienten,

\[p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} \hspace{0.05cm},\]

ein Erweiterungskörper GF(2²) formulieren. Im vorliegenden Fall gibt es nur ein geeignetes Polynom p₁(x) = x² + x + 1. Alle anderen möglichen Polynome vom Grad m = 2, nämlich

\[p_2(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},\] \[p_3(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},\] \[p_4(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^2 + x = (x+1) \cdot x \]

lassen sich faktorisieren und ergeben keinen Erweiterungskörper. Man nennt die Polynome p₂(x), p₃(x) und p₄(x) reduzibel.

Anmerkung: Die Umbenennung der Funktionsvariablen α in x hat nur formale Bedeutung im Hinblick auf die folgenden Seiten.

GF(2²) – Beispiel eines Erweiterungskörpers (3)

Wir betrachten weiterhin den Körper GF(2²) = {0, 1, α, 1+α} entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung p(α) = α² + α + 1 = 0 (irreduzibles Ploynom):

+	0	1	α	1+α
0	0	1	α	1+α
1	1	0	1+α	α
α	α	1+α	0	1
1+α	1+α	α	1	0

.	1	α	1+α
0	0	0	0
1	1	α	1+α
α	α	1+α	1
1+α	1+α	1	α

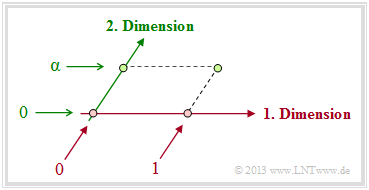
Welche Bedeutung hat aber nun das neue Element α?

Das Polynom p(α) = α² + α + 1 hat keine Nullstelle in GF(2) = {0, 1}. Das bedeutet weiter, dass α weder 0 noch 1 sein kann.

Wäre α = 0 bzw. α = 1, so wären zudem zwei der vier Mengenelemente {0, 1, α, 1+α} jeweils identisch. Entweder „0” und „α” sowie „1” und „1+α” oder „1” und „α” sowie „0” und „1+α”.

Vielmehr erhält der eindimensionale Körper GF(2) durch die Einführung des Elementes α eine zweite Dimension. Er wird also zum Galoisfeld GF(2²) erweitert, wie die folgende Grafik zeigt.

Das Element α hat ähnliche Bedeutung wie die imaginäre Einheit j, durch die man die Menge der reellen Zahlen unter der Nebenbedingung j² + 1 = 0 zur Menge der komplexen Zahlen erweitert.

Aufgrund der Identität α² = 1 + α, die aus der Nebenbedingung p(α) = 0 folgt, kann man in gleicher Weise GF(2²) = {0, 1, α, α²} schreiben, wobei nun folgende Operationstabellen gelten:

+	0	1	α	α²
0	0	1	α	α²
1	1	0	α²	α
α	α	α²	0	1
α²	α²	α	1	0

.	1	α	α²
0	0	0	0
1	1	α	α²
α	α	α²	1
α²	α²	1	α

Polynome über einem endlichen Körper (1)

Ein Polynom in einem endlichen Körper GF(P), wobei P eine Primzahl angibt, hat folgende Form:

\[a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm} + a_m \cdot x^{m} \hspace{0.05cm}.\]

Anzumerken ist:

Alle Koeffizienten sind Elemente des Körpers: a_i ∈ GF(P).

Ist der führende Koeffizient a_m ≠ 0, so gibt m den Grad des Polynoms an.

Betrachten wir ein dazu zweites Polynom mit Grad M,

\[b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm} + b_M \cdot x^{M} \hspace{0.05cm},\]

so erhält man für die Summe (bzw. Differenz) und das Produkt jeweils in GF(P):

\[a(x) \pm b(x) \hspace{-0.15cm} = \hspace{-0.15cm} \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},\] \[a(x) \cdot b(x) = \hspace{-0.15cm} \sum_{i = 0}^{m + M} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]

: Es gelte a(x) = x³ + x + 1 und b(x) = x² + x + 1. Im binären Galoisfeld ⇒ GF(2) ergibt sich nach den obigen Gleichungen für die Summe, die Differenz und das Produkt der beiden Polynome:

\[s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, \hspace{0.5cm} d(x) = a(x) - b(x) = x^3 + x^2 = s(x)\hspace{0.05cm},\]

\[c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]

Mit a₀ = a₁ = a₃ = b₀ = b₁ = b₂ = 1 und a₂ = a₄ = a₅ = b₃ = b₄ = b₅ = 0 erhält man:

\[c_0 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},\] \[c_1 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_1 + a_1 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\] \[c_2 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_2 + a_1 \cdot b_1 + a_2 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 0 \hspace{0.05cm},\] \[c_3 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_3 + a_1 \cdot b_2 + a_2 \cdot b_1 + a_3 \cdot b_0 = 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\] \[c_4 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_4 + a_1 \cdot b_3 + \hspace{0.05cm}...+ \hspace{0.05cm}a_4 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 1 \hspace{0.05cm},\] \[c_5 \hspace{-0.25cm} = \hspace{-0.15cm} a_0 \cdot b_5 + a_1 \cdot b_4 + \hspace{0.05cm}...+ \hspace{0.05cm} a_5 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 0 \cdot 1= 1 \]

\[\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.\]

Im Galoisfeld GF(3) erhält man aufgrund der Modulo–3–Operationen andere Ergebnisse:

\[s(x) \hspace{-0.15cm} = \hspace{-0.15cm} (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},\] \[d(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^3 + x + 1) - (x^2 + x + 1) = x^3 + 2x^2 \hspace{0.05cm},\]

\[c(x) \hspace{-0.15cm} = \hspace{-0.15cm} x^3 + x + 1) \cdot (x^2 + x + 1) = x^5 + x^4 + 2x^3 + 2x^2 + 2x +1\hspace{0.05cm}.\]

Polynome über einem endlichen Körper (2)

: Ein Polynom a(x) bezeichnet man als reduzibel (englisch: reducible), wenn es als Produkt zweier Polynome p(x) und q(x) mit jeweils niedrigerem Grad dargestellt werden kann:

\[a(x) = p(x) \cdot q(x) \hspace{0.05cm}.\]

Ist diese Faktorisierung nicht möglich, das heißt, wenn

\[a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0\]

gilt, so spricht man von einem irreduziblen (englisch: irreducible oder prime) Polynom.

: Es gelte b(x) = x³ + x + 1, p₁(x) = x² + x + 1 und p₂(x) = x² + 1. Die Grafik verdeutlicht links die Modulo–2–Multiplikation a(x) = b(x) · p₁(x). Das Ergebnis ist a(x) = x⁵ + x⁴ + 1.

Im rechten Teil der obigen Grafik ist die Modulo–2–Division q(x) = a(x)/p₂(x) mit dem Ergebnis q(x) = x³ + x² + x + 1 dargestellt. Es verbleibt der Rest r(x) = x. Allein nach dieser Rechnung könnte a(x) = x⁵ + x⁴ + 1 durchaus ein irreduzibles Polynom sein.

Der Nachweis, dass das Polynom a(x) = x⁵ + x⁴ + 1 tatsächlich irreduzibel ist, wäre allerdings erst dann erbracht, wenn a(x)/p(x) für alle

\[p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}... \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}\]

einen Rest r(x) ≠ 0 liefert. Dies würde im vorliegenden Beispiel (nahezu) 2⁵ = 32 Divisionen erfordern.

Aufgrund unserer linken Berechnung können wir hier sofort erkennen, dass a(x) mit Sicherheit kein irreduzibles Polynom ist, da zum Beispiel a(x) = x⁵ + x⁴ + 1 dividiert durch p₁(x) = x² + x + 1 das Polynom b(x) = x³ + x + 1 ohne Rest ergibt.

Verallgemeinerte Definition eines Erweiterungskörpers

Wir gehen von folgenden Voraussetzungen aus:

einem Galoisfeld GF(P), wobei P eine Primzahl angibt,

einem irreduziblen Polynom p(x) über GF(P) mit dem Grad m:

\[p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}... \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} a_i \in {\rm G}(P)\hspace{0.05cm}, \hspace{0.15cm}a_m \ne 0\hspace{0.05cm}. \]

Mit den genannten Voraussetzungen gilt allgemein:

: Es sei P eine Primzahl, m ganzzahlig, p(x) ein irreduzibles Polynom vom Grad m und es gelte p(α) = 0. Ein Erweiterungskörper lässt sich dann wie folgt beschreiben.

\[{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}... \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{|}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}... \hspace{0.05cm}, P-1\}\Big \}\]

Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der Polynomaddition und Polynommultiplikation modulo p(α).

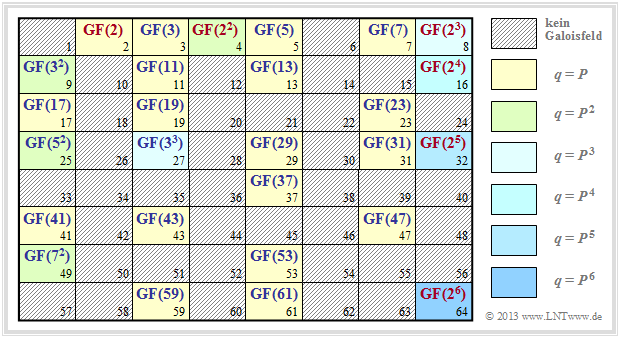
Ein Galoisfeld GF(q) mit q Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form q = P^m geschrieben werden kann (P kennzeichnet eine Primzahl, m sei ganzzahlig).

Die Grafik zeigt, für welche q–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten q–Werte ist kein endlicher Körper angebbar. Weiter ist anzumerken:

Die gelb hinterlegten Positionen q = P ⇒ m = 1 markieren Zahlenmengen {0, 1, ... , q – 1} mit Galoiseigenschaften, siehe Kapitel 2.1.

Die anderen farblich hinterlegten Positionen markieren Erweiterungskörper mit q = P^m, m ≥ 2. Für q ≤ 64 basieren diese auf den Primzahlen 2, 3, 5 und 7.

Mit roter Schrift hervorgehoben sind binäre Körper ⇒ q = 2^m, m ≥ 1, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.

Binäre Erweiterungskörper (1)

Im Folgenden betrachten wir binäre Erweiterungskörper mit

\[q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4, 8, 16, 32, 64, ...\]

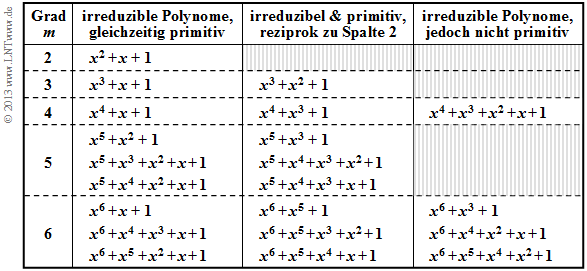
Elementen. In der Tabelle sind für 2 ≤ m ≤ 6 alle irreduziblen Polynome des Galoisfeldes GF(2) angegeben. Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern auch primitiv.

Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten primitiver Elemente am Beispiel von

\[{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.1cm} ... , \hspace{0.05cm}z_{q-1}\}\]

genannt werden. Das Element z_i = β wird dann als primitiv bezeichnet,

wenn die Potenz βⁱ modulo q zum ersten Mal für i = q – 1 das Ergebnis „1” liefert,

so dass βⁱ für 1 ≤ i ≤ q – 1 genau die Elemente z₁, ... , z_q–1 liefert, also alle Elemente von GF(q) mit Ausnahme des Nullelementes z₀ = 0.

: Von der Zahlenmenge Z₅ = {0, 1, 2, 3, 4} sind „2” und „3” wegen

\[2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\] \[3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\]

primitive Elemente. Dagegen ist „4” kein primitives Element, weil bereits 4² = 1 ist:

\[4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.\]

Binäre Erweiterungskörper (2)

: Ein irreduzibles Polynom bezeichnet man gleichzeitig als ein primitives Polynom, wenn die Wurzel α bezüglich des Polynoms p(x) ein primitives Element von GF(q) ist. Dann gilt \[{\rm GF}(q) = \{\hspace{0.1cm}\alpha^{-\infty} = 0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2},\hspace{0.1cm} ... \hspace{0.1cm} , \hspace{0.1cm}\alpha^{q-2}\hspace{0.1cm}\}\hspace{0.05cm}. \]

Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv. Ist p₁(x) ein primitives Polynom, so ist auch das dazu reziproke Polynom

\[p_2 (x) = x^m \cdot p_1(x^{-1})\]

primitiv. Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für m = 3:

\[p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot [x^{-3} + x^{-1} + 1 ]= x^3 + x^2 + 1 \hspace{0.05cm}.\]

Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.

Hinweis: Primitive Polynome liefern auch die Grundlage für Pseudo–Noise–Generatoren.

: Zur Verdeutlichung dieser Aussagen betrachten wir beispielhaft

das Galoisfeld GF(2³) = GF(8), sowie
das Polynom p(x) = x³ + x + 1.

Aus der Bedingung p(α) = 0 erhält man in GF(2³) weiter:

\[\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},\]

und damit für die Potenzen αⁱ der Wurzel für i ≥ 4:

\[\alpha^4 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},\] \[\alpha^5 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^2 \cdot \alpha^3 = \alpha^2 \cdot (\alpha + 1) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1 \hspace{0.05cm},\] \[\alpha^6 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^3 \cdot \alpha^3 = (\alpha + 1) \cdot (\alpha + 1) = \alpha^2 + \alpha + \alpha + 1= \alpha^2 + 1 \hspace{0.05cm},\]

\[\alpha^7 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^4 \cdot \alpha^3 = (\alpha^2 + \alpha) \cdot (\alpha + 1) = \alpha^3 + \alpha^2 + \alpha^2 + \alpha = \alpha + 1 + \alpha = 1 = \alpha^0 \hspace{0.05cm}.\]

Binäre Erweiterungskörper (3)

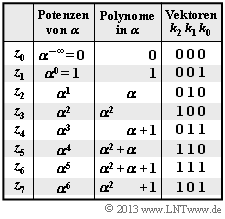
Elemente von GF(23) in drei verschiedenen Darstellungen

Die Elemente z₀, z₁, ... , z₇ des Galoisfeldes GF(2³) lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen:

als Potenzen von α (Exponentendarstellung),

als Polynome der Form k₂ · α² + k₁ · α + k₀ mit binären Koeffizienten k₂, k₁, k₀ (jeweils 0 oder 1) ,

als Vektoren der Koeffizienten (k₂, k₁, k₀).

Für die Addition (oder Subtraktion) zweier Elemente eignen sich die Polynom– und die Vektordarstellung gleichermaßen, wobei die Komponenten modulo 2 zu addieren sind, zum Beispiel:

\[z_5 + z_7 \hspace{-0.15cm} = \hspace{-0.15cm} (\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},\] \[{\rm oder}\hspace{0.15cm} z_5 + z_7 \hspace{-0.15cm} = \hspace{-0.15cm} (110) + (101) = (011) = z_4 \hspace{0.05cm},\] \[\hspace{0.15cm} z_1 + z_2 + z_3 \hspace{-0.15cm} = \hspace{-0.15cm} (001) + (010) + (100)= (111) = z_6 \hspace{0.05cm}.\]

Für Multiplikationen ist die Exponentendarstellung besser geeignet, wie die folgenden Beispiele zeigen:

\[z_3 \cdot z_4 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},\] \[z_0 \cdot z_5 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},\] \[z_5 \cdot z_7 \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^4 \cdot \alpha^6 = \alpha^{10}= \alpha^{7} \cdot \alpha^{3} = 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.\]

Man erkennt, dass sich hierbei die Exponenten modulo (q – 1) ergeben; im Beispiel modulo 7.

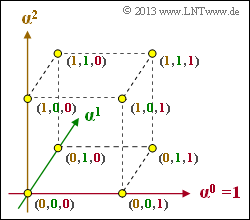
Die Grafik zeigt den endlichen Erweiterungskörper GF(2³) in einer 3D–Darstellung, wobei die Achsen mit α⁰ = 1, α¹ und α² bezeichnet sind. Die 2³ = 8 Punkte im dreidimensionalen Raum sind mit den Koeffizientenvektoren beschriftet, wobei die Zuordnung der einzelnen Koeffizienten k₂, k₁, k₀ zu den Achsen farblich deutlich gemacht ist.