Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken

Freie Distanz vs. Minimale Distanz

Eine äußerst wichtige Kenngröße hinsichtlich der Fehlerwahrscheinlichkeit eines linearen Blockcodes ist die minimale Distanz zwischen zwei Codeworten:

\[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]

Der zweite Gleichungsteil ergibt sich aus der Tatsache, dass jeder lineare Code auch das Nullwort (0) beinhaltet. Zweckmäßigerweise setzt man deshalb x' = 0, so dass die Hamming–Distanz d_H(x, 0) das gleiche Ergebnis liefert wie das Hamming–Gewicht w_H(x).

: Beispiel: Die nachfolgende Tabelle zeigt die 16 Codeworte des (7, 4, 3)–Hamming–Codes.

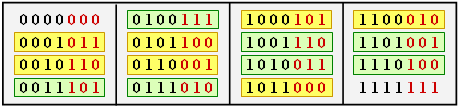
Alle Codeworte außer dem Nullwort (0) beinhalten mindestens drei Einsen ⇒ d_min = 3. Es gibt sieben Codeworte mit drei Einsen, sieben mit vier Einsen und je eines ohne Einsen bzw. mit sieben Einsen.

Die freie Distanz d_F eines Faltungscodes (Convolution Code ⇒ CC) unterscheidet sich formelmäßig nicht von der minimalen Distanz eines linearen Blockcodes:

\[d_{\rm F}(\mathcal{CC}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]

In der Literatur wird anstelle von d_F teilweise auch d_∞ verwendet.

Wesentlicher Unterschied zur minimalen Distanz ist, dass bei Faltungscodes nicht Informations– und Codeworte zu betrachten sind, sondern Sequenzen mit der Eigenschaft semi–infinite.

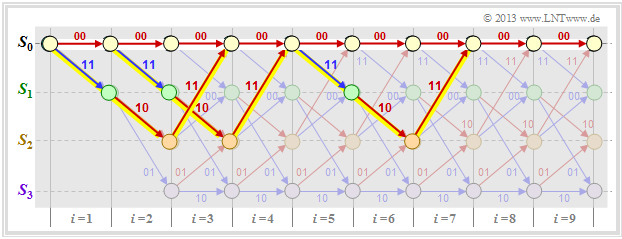
Jede Codesequenz x beschreibt einen Pfad durch das Trellis. Die freie Distanz ist dabei das kleinstmögliche Hamming–Gewicht eines solchen Pfades (mit Ausnahme des Nullpfades).

Die Grafik zeigt drei der unendlich vielen Pfade mit dem minimalen Hamming–Gewicht w_H(x) = d_F = 5.

Pfadgewichtsfunktion (1)

Für jeden linearen Blockcode lässt sich wegen der endlichen Anzahl an Codeworten x in einfacher Weise eine Gewichtsfunktion angeben. Für das Beispiel auf der letzten Seite lautet diese:

\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]

Bei einem (nicht terminierten) Faltungscode kann keine solche Gewichtsfunktion angegegeben werden, da es unendlich viele, unendlich lange Codesequenzen x gibt, und damit auch unendlich viele Trellispfade. Um dieses Problem in den Griff zu bekommen, gehen wir nun von folgenden Voraussetzungen aus:

Als Bezugsgröße für das Trellisdiagramm wählen wir stets den Pfad der Codesequenz x = 0 und nennen diesen den Nullpfad φ₀.

Desweiteren betrachten wir nur noch solche Pfade φ_j ∈ Φ, die alle zu einer vorgegebenen Zeit t vom Nullpfad abweichen und irgendwann wieder zu diesem zurückkehren.

Obwohl nur ein Bruchteil aller Trellispfade zu dieser Menge Φ gehören, beinhaltet Φ = {φ₁, φ₂, φ₃, ...} noch immer eine unbegrenzte Menge an Pfaden. φ₀ gehört nicht zu dieser Menge.

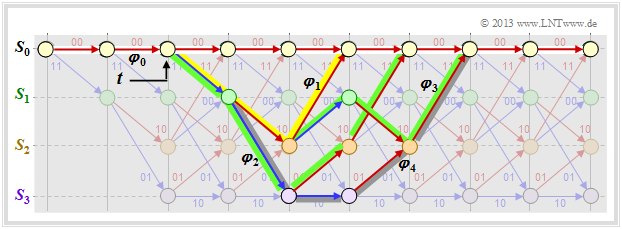
Im obigen Trellis sind einige Pfade φ_j ∈ Φ eingezeichnet:

Der gelbe Pfad φ₁ gehört zur Sequenz x₁ = (11, 10, 11) mit dem Hamming–Gewicht w_H(x₁) = 5. Damit ist auch das Pfadgewicht w(φ₁) = 5. Aufgrund der Festlegung des Abzweigzeitpunktes t hat nur noch dieser einzige Pfad φ₁ die freie Distanz d_F = 5 zum Nullpfad ⇒ A₅ = 1.

Für die beiden grünen Pfade mit den korrespondierenden Sequenzen x₂ = (11, 01, 01, 11) bzw. x₃ = (11, 10, 00, 10, 11) gilt w(φ₂) = w(φ₃) = 6. Kein anderer Pfad weist das Pfadgewicht 6 auf. Wir berücksichtigen diese Tatsache durch den Koeffizienten A₆ = 2.

Eingezeichnet ist auch der graue Pfad φ₄, assoziiert mit der Sequenz x₄ = (11, 01, 10, 01, 11) ⇒ w(φ₄) = 7. Auch die Sequenzen x₅ = (11, 01, 01, 00, 10, 11), x₆ = (11, 10, 00, 01, 01, 11) und x₇ = (11, 10, 00, 10, 00, 10, 11) weisen jeweils das gleiche Pfadgewicht 7 auf ⇒ A₇ = 4.

Damit lautet die Pfadgewichtsfunktion (englisch: Path Weight Enumerator Function, PWEF):

\[T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + ... \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ ... \hspace{0.1cm} \hspace{0.05cm}.\]

Die Definition dieser Funktion T(X) wird auf der nächsten Seite nachgeliefert.