Algebraische und polynomische Beschreibung

1. Kanalcodierung
2. Faltungscodierung und geeignete Decoder
3. Algebraische und polynomische Beschreibung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Definition und Interpretation der Teilmatrizen G0, ... , Gm

Entsprechend den Ausführungen in Kapitel 1.4 lässt sich das Codewort x eines linearen Blockcodes aus dem Informationswort u und der Generatormatrix G in einfacher Weise ermitteln:

\[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]

Dabei gilt:

• Die Vektoren u und x haben die Länge k (Bitanzahl eines Informationswortes) bzw. n (Bitanzahl eines Codewortes) und G besitzt die Dimension k × n (k Zeilen und n Spalten).
  

• Bei Faltungscodierung bezeichnen dagegen u und x Sequenzen mit k' → ∞ und n' → ∞. Deshalb wird auch die Generatormatrix G in beiden Richtungen unendlich weit ausgedehnt sein.
  
  

Als Vorbereitung für die Einführung der Generatormatrix G auf der nächsten Seite definieren wir m + 1 Teilmatrizen, jeweils mit k Zeilen und n Spalten, die wir mit G_l bezeichnen, wobei 0 ≤ l ≤ m gilt.

: Ist das Matrizenelement G_l(κ, j) = 1, so sagt dies aus, dass das Codebit x_i^(j) durch das Informationsbit u_i–l^(κ) beeinflusst wird. Andernfalls ist dieses Matrixelement gleich 0.

Diese Definition wird nun an einem Beispiel verdeutlicht.

:

Wir betrachten wiederum den Faltungscodierer gemäß nebenstehender Grafik mit den folgenden Codebits:

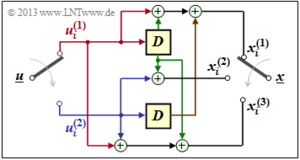
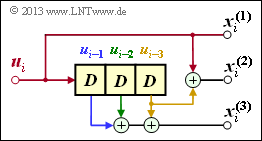
\[x_i^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i-1}^{(1)}+ u_{i-1}^{(2)} \hspace{0.05cm},\] \[x_i^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(2)} + u_{i-1}^{(1)} \hspace{0.05cm},\] \[x_i^{(3)} \hspace{-0.15cm} = \hspace{-0.15cm} u_{i}^{(1)} + u_{i}^{(2)}+ u_{i-1}^{(1)} \hspace{0.05cm}.\]

Wegen der Gedächtnisordnung m = 1 wird dieser Codierer durch die beiden Teilmatrizen G₀ und G₁ charakterisiert:

\[{ \boldsymbol{\rm G}}_0 = \begin{pmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 & 1 & 1\\ 1 & 0 & 0 \end{pmatrix}\hspace{0.05cm}.\]

Diese Matrizen sind wie folgt zu interpretieren:

• Erste Zeile von G₀, rote Pfeile:       u_i⁽¹⁾ beeinflusst sowohl x_i⁽¹⁾ als auch x_i⁽³⁾, nicht jedoch x_i⁽²⁾.
  

• Zweite Zeile von G₀, blaue Pfeile:   u_i⁽²⁾ beeinflusst x_i⁽²⁾ und x_i⁽³⁾, aber nicht x_i⁽¹⁾.
  

• Erste Zeile von G₁, grüne Pfeile:     u_i–1⁽¹⁾ beeinflusst alle drei Coderausgänge.
  

• Zweite Zeile von G₁, brauner Pfeil: u_i–1⁽²⁾ beeinflusst nur x_i⁽¹⁾.

Generatormatrix eines Faltungscodierers mit Gedächtnis m

Mit den Teilmatrizen G₀, ... , G_m lassen sich die n Codebits zum Zeitpunkt i wie folgt ausdrücken:

\[\underline{x}_i = \sum_{l = 0}^{m} \hspace{0.15cm}\underline{u}_{i-l} \cdot { \boldsymbol{\rm G}}_l = \underline{u}_{i} \cdot { \boldsymbol{\rm G}}_0 + \underline{u}_{i-1} \cdot { \boldsymbol{\rm G}}_1 + ... + \underline{u}_{i-m} \cdot { \boldsymbol{\rm G}}_m \hspace{0.05cm}.\]

Hierbei sind folgende vektorielle Größen zu berücksichtigen:

\[\underline{\it u}_i = \left ( u_i^{(1)}, u_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, u_i^{(k)}\right )\hspace{0.05cm},\hspace{0.5cm} \underline{\it x}_i = \left ( x_i^{(1)}, x_i^{(2)}, \hspace{0.05cm}... \hspace{0.1cm}, x_i^{(n)}\right )\hspace{0.05cm}.\]

Betrachtet man die bei i = 1 beginnenden und sich zeitlich bis ins Unendliche erstreckenden Sequenzen

\[\underline{\it u} = \big( \underline{\it u}_1\hspace{0.05cm}, \underline{\it u}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it u}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\hspace{0.5cm} \underline{\it x} = \big( \underline{\it x}_1\hspace{0.05cm}, \underline{\it x}_2\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm}, \underline{\it x}_i\hspace{0.05cm}, \hspace{0.05cm}... \hspace{0.1cm} \big)\hspace{0.05cm},\]

so kann dieser Zusammenhang durch die Matrixgleichung x = u · G ausgedrückt werden. Hierbei ist für die Generatormatrix G zu setzen:

\[{ \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \cdots & \cdots & & & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Aus der Gleichung erkennt man sofort das Gedächtnis m des Faltungscodes. Die Parameter k und n sind direkt nicht ablesbar. Sie sind aber durch die Zeilen– und Spaltenzahl der Teilmatrizen G_l festgelegt.

:

Mit den zwei Matrizen G₀ und G₁ – siehe letztes Beispiel – erhält man die rechts skizzierte Matrix G.

Anzumerken ist:

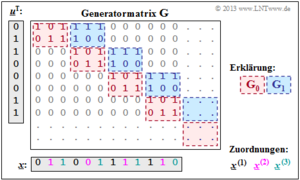
• Die Generatormatrix G erstreckt sich nach unten und nach rechts eigentlich bis ins Unendliche. Explizit dargestellt sind aber nur 8 Zeilen und 12 Spalten.

• Für die zeitlich begrenzte Informationssequenz u = (0, 1, 1, 0, 0, 0, 1, 1) ist der gezeichnete Matrixteil ausreichend. Die Codesequenz lautet dann:   x = (0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0).

• Anhand der Beschriftungsfarben lassen sich die n = 3 Codewortstränge ablesen. Das gleiche Ergebnis haben wir (auf anderem Wege) im Beispiel am Ende von Kapitel 3.1 erhalten.

\[\underline{\it x}^{(1)} = (0\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(2)} = (1\hspace{0.05cm}, 0\hspace{0.05cm},1\hspace{0.05cm}, 1) \hspace{0.05cm},\hspace{0.5cm} \underline{\it x}^{(3)} = (1\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0) \hspace{0.05cm}.\]

Generatormatrix für Faltungscodierer der Rate 1/n

Wir betrachten nun den Sonderfall k = 1, zum einen aus Gründen einer möglichst einfachen Darstellung, aber auch, weil Faltungscodierer der Rate 1/n für die Praxis eine große Bedeutung besitzen.

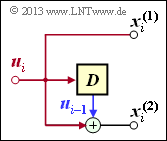
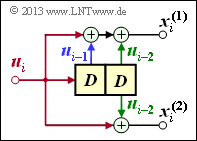
Faltungscodierer mit k = 1, n = 2 und m = 1

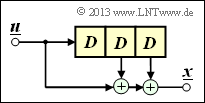
Aus der nebenstehenden Skizze kann abgeleitet werden:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 1 \end{pmatrix}\]

\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 01 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 01 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 01 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 01 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Für die Eingangssequenz u = (1, 0, 1, 1) beginnt die Codesequenz mit x = (1, 1, 0, 1, 1, 1, 1, 0, ...). Dieses Ergebnis ist gleich der Summe der Zeilen 1, 3 und 4 der Gewneratormatrix.

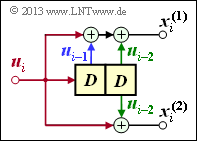
Faltungscodierer mit k = 1, n = 2 und m = 2

Aufgrund der Gedächtnisordnung m = 2 gibt es hier drei Teilmatrizen:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_2=\begin{pmatrix} 1 & 1 \end{pmatrix}\]

\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm G}}=\begin{pmatrix} 11 & 10 & 11 & 00 & 00 & 00 & \cdots & \\ 00 & 11 & 10 & 11 & 00 & 00 & \cdots & \\ 00 & 00 & 11 & 10 & 11 & 00 & \cdots & \\ 00 & 00 & 00 & 11 & 10 & 11 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm}.\]

Hier führt die Eingangsssequenz u = (1, 0, 1, 1) zur Codesequenz x = (1, 1, 1, 0, 0, 0, 0, 1, ...).

Faltungscodierer mit k = 1, n = 3 und m = 3

Wegen m = 3 gibt es vier Teilmatrizen der Dimension 1 × 3:

\[{ \boldsymbol{\rm G}}_0=\begin{pmatrix} 1 & 1 & 0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_1=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]

\[{ \boldsymbol{\rm G}}_2=\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} { \boldsymbol{\rm G}}_3=\begin{pmatrix} 0 & 1 & 1 \end{pmatrix}\hspace{0.05cm}.\]

Damit lautet die resultierende Generatormatrix:

\[{ \boldsymbol{\rm G}}=\begin{pmatrix} 110 & 001 & 001 & 011 & 000 & 000 & 000 & \cdots & \\ 000 & 110 & 001 & 001 & 011 & 000 & 000 & \cdots & \\ 000 & 000 & 110 & 001 & 001 & 011 & 000 & \cdots & \\ 000 & 000 & 000 & 110 & 001 & 001 & 011 & \cdots & \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{pmatrix}\hspace{0.05cm},\]

und man erhält für u = (1, 0, 1, 1) die Codesequenz x = (1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, ...).

GF(2)–Beschreibungsformen eines Digitalen Filters (1)

In Kapitel 3.1 wurde bereits darauf hingewiesen, dass ein Faltungscodierer der Rate 1/n durch mehrere Digitale Filter realisiert werden kann, wobei die Filter parallel mit der gleichen Eingangsfolge u arbeiten. Bevor wir diese Aussage vertiefen, sollen zuerst die Eigenschaften eines Digitalfilters für das Galoisfeld GF(2) genannt werden.

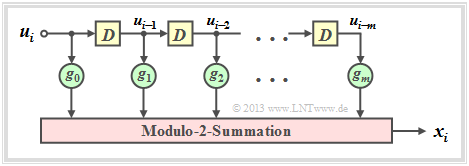
Die Grafik ist wie folgt zu interpretieren:

• Das Filter besitzt die Impulsantwort g = (g₀, g₁, g₂, ... , g_m), wobei für alle Filterkoeffizienten (mit den Indizes 0 ≤ l ≤ m) gilt:   g_l ∈ GF(2) = {0, 1}.
  

• Die einzelnen Symbole u_i der Eingangsfolge u seien ebenfalls binär: u_i ∈ {0, 1}. Damit gilt für das Ausgangssymbol zu den Zeitpunkten i ≥ 1 mit Addition und Multiplikation in GF(2):

\[x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l} \hspace{0.05cm}.\]

• Dies entspricht der (zeitdiskreten) Faltungsoperation (englisch: Convolution), gekennzeichnet durch einen Stern. Damit kann für die gesamte Ausgangssequenz geschrieben werden:

\[\underline{x} = \underline{u} * \underline{g}\hspace{0.05cm}.\]

• Wesentlicher Unterschied gegenüber dem Kapitel 5.2 des Buches „Stochastische Signaltheorie” ist die Modulo–2–Addition (1 + 1 = 0) anstelle der herkömmlichen Addition (1 + 1 = 2).
  
  

:

Die Impulsantwort des dargestellten Digitalen Filters der Ordnung 3 lautet g = (1, 0, 1, 1).

Die Eingangssequenz dieses Filters sei zeitlich unbegrenzt:   u = (1, 1, 0, 0, 0, ...).

Damit ergibt sich die (unendliche) Ausgangssequenz x im binären Galoisfeld ⇒ GF(2):

\[\underline{x} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0, \hspace{0.05cm}. ... \hspace{0.05cm}) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1\hspace{0.05cm})= \] \[\hspace{0.3cm} = \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}0,\hspace{0.05cm} . ... \hspace{0.05cm}) \oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm}0, \hspace{0.05cm} . ... \hspace{0.05cm}) = (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Bei der herkömmlichen Faltung (für reelle Zahlen) hätte dagegen das Ergebnis gelautet:

\[\underline{x}= (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 1,\hspace{0.05cm} 0, . ... \hspace{0.05cm}) \hspace{0.05cm}.\]

GF(2)–Beschreibungsformen eines Digitalen Filters (2)

Zeitdiskrete Signale kann man auch durch Polynome bezüglich einer Dummy–Variablen repräsentieren.

: Die zum zeitdiskreten Signal x = (x₀, x₁, x₂, ...) gehörige D–Transformierte lautet:

\[X(D) = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \hspace{0.05cm}...\hspace{0.05cm}= \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]

Für diese spezielle Transformation in einen Bildbereich verwenden wir auch die Notation:

\[\underline{x} = (x_0, x_1, x_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = \sum_{i = 0}^{\infty} x_i \cdot D^i \hspace{0.05cm}.\]

In der Literatur wird manchmal x(D) anstelle von X(D) verwendet. Wir schreiben in LNTwww aber alle Bildbereichsfunktionen mit Großbuchstaben, zum Beispiel Fourier–, Laplace– und D–Transformation:

\[x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}}\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)\hspace{0.05cm},\hspace{0.4cm} x(t) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\hspace{0.15cm} X(p) \hspace{0.05cm},\hspace{0.4cm} \underline{x} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} X(D) \hspace{0.05cm}.\]

Wir werden nun die D–Transformation auch auf die Informationssequenz u und die Impulsantwort g an. Aufgrund der zeitlichen Begrenzung von g ergibt sich die obere Summationsgrenze bei G(D) zu i = m:

\[\underline{u} = (u_0, u_1, u_2,\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = \sum_{i = 0}^{\infty} u_i \cdot D^i \hspace{0.05cm},\]

\[\underline{g} = (g_0, g_1, \hspace{0.05cm}...\hspace{0.05cm}, g_m) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = \sum_{i = 0}^{m} g_i \cdot D^i \hspace{0.05cm}.\]

: Wie bei allen Spektraltransformationen gilt auch bei der D–Transformation im Bildbereich die Multiplikation, da die (diskreten) Zeitsignale u und g durch die Faltung verknüpft sind:

\[\underline{x} = \underline{u} * \underline{g} \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad X(D) = U(D) \cdot G(D) \hspace{0.05cm}.\]

Man bezeichnet, wie in der Systemtheorie allgemein üblich, auch die D–Transformierte G(D) der Impulsantwort g als Übertragungsfunktion (englisch: Transfer Function).

Der (recht einfache) Beweis dieses wichtigen Ergebnisses finden Sie in der Angabe zu Aufgabe Z3.3.

:

Wir betrachten wieder die zeitdiskreten Signale

\[\underline{u} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}...\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D \hspace{0.05cm},\]

\[\underline{g} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 + D^3 \hspace{0.05cm}.\]

Wie im letzten Biespiel: erhält man auch auf diesem Lösungsweg:

\[X(D) \hspace{-0.15cm} = \hspace{-0.15cm} U(D) \cdot G(D) = (1+D) \cdot (1+ D^2 + D^3) =\] \[\hspace{1cm} = \hspace{-0.15cm} 1+ D^2 + D^3 +D + D^3 + D^4 = 1+ D + D^2 + D^4 \]

\[\Rightarrow \hspace{0.4cm} \underline{x} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Die Multiplikation mit D im Bildbereich entspricht im Zeitbereich einer Verschiebung um eine Stelle nach rechts, weshalb man D als Verzögerungsoperator (englisch: Delay Operator) bezeichnet:

\[W(D) = D \cdot X(D) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\circ\quad \underline{w} = (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, ... \hspace{0.05cm}) \hspace{0.05cm}.\]

Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (1)

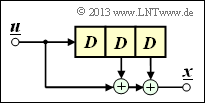
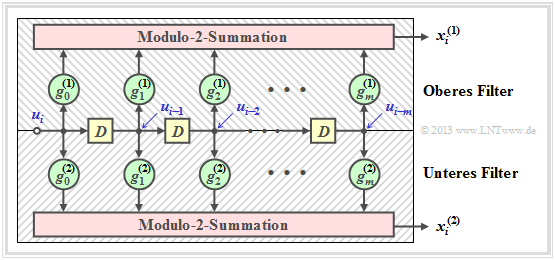
Wir wenden nun die Ergebnisse der letzten Seite auf einen Faltungscoder an, wobei wir uns zunächst auf den Sonderfall k = 1 beschränken. Ein solcher (n, k = 1)–Faltungscode lässt sich mit n Digitalen Filtern realisieren, die auf der gleichen Informationssequenz u parallel arbeiten. Die Grafik zeigt die Anordnung für den Codeparameter n = 2  ⇒  Coderate R = 1/2.

Die nachfolgenden Gleichungen gelten für beide Filter gleichermaßen, wobei für das obere Filter j = 1 und für das untere Filter j = 2 zu setzen ist:

• Die Impulsantworten der beiden Filter ergeben sich zu

\[\underline{g}^{(j)} = (g_0^{(j)}, g_1^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}, g_m^{(j)}\hspace{0.01cm}) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

• Die beiden Ausgangssequenzen lauten:

\[\underline{x}^{(j)} = (x_0^{(j)}, x_1^{(j)}, x_2^{(j)}, \hspace{0.05cm}...\hspace{0.05cm}) = \underline{u} \cdot \underline{g}^{(j)} \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

Hierbei ist berücksichtigt, dass das obere Filter und das untere Filter beide auf der gleichen Eingangssequenz u = (u₀, u₁, u₂, ...) arbeiten.

• Für die D–Transformierten der Ausgangssequenzen gilt:

\[X^{(j)}(D) = U(D) \cdot G^{(j)}(D) \hspace{0.05cm},\hspace{0.2cm}{\rm mit }\hspace{0.15cm} j \in \{1,2\}\hspace{0.05cm}.\]

Auf der nächsten Seite verwenden wir eine kompaktere Schreibweise.

Anwendung der D–Transformation auf Rate–1/n–Faltungscoder (2)

Um den soeben dargelegten Sachverhalt kompakter darstellen zu können, definieren wir nun folgende vektorielle Größen eines Faltungscodes der Rate 1/n:

: Die D–Übertragungsfunktionen der n parallel angeordneten digitalen Filter werden im Vektor G(D) zusammengefasst:

\[\underline{G}(D) = \left ( G^{(1)}(D), G^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, G^{(n)} (D) \right )\hspace{0.05cm}.\]

Der Vektor X(D) beinhaltet die D–Transformierten der n Codesequenzen x⁽¹⁾, x⁽²⁾, ... , x⁽ⁿ⁾:

\[\underline{X}(D) = \left ( X^{(1)}(D), X^{(2)}(D), \hspace{0.05cm}...\hspace{0.1cm}, X^{(n)} (D) \right )\hspace{0.05cm}.\]

Damit erhält man die folgende Vektorgleichung:

\[\underline{X}(D) = U(D) \cdot \underline{G}(D)\hspace{0.05cm}.\]

Aufgrund des Codeparameters k = 1 ist U(D) hier keine vektorielle Größe.

:

Wir betrachten beispielhaft den skizzierten Faltungscode mit den Codeparametern n = 2, k = 1 und m = 2. Für diesen gilt:

\[\underline{g}^{(1)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D + D^2 \hspace{0.05cm},\] \[\underline{g}^{(2)} \hspace{-0.15cm} = \hspace{-0.15cm} (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1+ D^2 \]

\[\Rightarrow \hspace{0.3cm} \underline{G}(D) = \big ( 1+ D + D^2 \hspace{0.05cm}, \hspace{0.1cm}1+ D^2 \big )\hspace{0.05cm}.\]

Die Informationssequenz sei u = (1, 0, 1, 1), was zur D–Transformierten U(D) = 1 + D² + D³ führt. Damit erhält man

\[\underline{X}(D) = \left ( X^{(1)}(D),\hspace{0.1cm} X^{(2)}(D) \right ) = U(D) \cdot \underline{G}(D) \hspace{0.05cm}, \hspace{0.2cm}\]

wobei

\[{X}^{(1)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D + D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D + D^2 + D^2 + D^3 + D^4 + D^3 + D^4 + D^5 = 1+ D + D^5\]

\[\Rightarrow \underline{x}^{(1)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm},\]

\[{X}^{(2)}(D) \hspace{-0.15cm} = \hspace{-0.15cm} (1+ D^2 + D^3) \cdot (1+ D^2)=\] \[\hspace{1.5cm} = \hspace{-0.15cm}1+ D^2 + D^2 + D^4 + D^3 + D^5 = 1+ D^3 + D^4 + D^5\]

\[\Rightarrow \underline{x}^{(2)} = (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} ... \hspace{0.05cm} \hspace{0.05cm}) \hspace{0.05cm}.\]

Das gleiche Ergebnis haben wir in der Aufgabe Z3.1 auf anderem Wege erhalten. Nach dem Multplexen der beiden Sränge erhält man wieder:   x = (11, 10, 00, 01, 01, 11, 00, 00, ... ).