Entropiecodierung nach Huffman
Inhaltsverzeichnis
Der Huffman–Algorithmus
Wir setzen nun voraus, dass die Quellensymbole qν einem Alphabet $\{q_μ\}$ = {A, B, C, ...} mit dem Symbolumfang M entstammen und statistisch voneinander unabhängig seien. Beispielsweise gelte für den Symbolumfang $M$ = 8:
$$\{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm}, \boldsymbol{\rm B}\hspace{0.05cm}, \boldsymbol{\rm C}\hspace{0.05cm}, \boldsymbol{\rm D}\hspace{0.05cm}, \boldsymbol{\rm E}\hspace{0.05cm}, \boldsymbol{\rm F}\hspace{0.05cm}, \boldsymbol{\rm G}\hspace{0.05cm}, \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
David A. Huffman hat 1952 – also kurz nach Shannons bahnbrechenden Veröffentlichungen – einen Algorithmus zur Konstruktion von optimalen präfixfreien Codes angegeben. Dieser Huffman–Algorithmus soll hier ohne Herleitung und Beweis angegeben werden, wobei wir uns hier auf Binärcodes beschränken. Das heißt: Für die Codesymbole gelte stets $c_ν$ ∈ {0, 1}. Hier ist das Rezept:
- Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten.
- Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen.
- Man wiederhole (1) und (2), bis nur mehr zwei (zusammengefasste) Symbole übrig bleiben.
- Man codiert die wahrscheinlichere Symbolmenge mit 1 und die andere Menge mit 0.
- Man ergänzt in Gegenrichtung (also von unten nach oben) die jeweiligen Binärcodes der aufgespaltenen Teilmengen entsprechend den Wahrscheinlichkeiten mit 1 bzw. 0.
Ohne Einschränkung der Allgemeingültigkeit setzen wir voraus, dass die $M$ = 6 Symbole A, ... , F bereits entsprechend ihren Wahrscheinlichkeiten geordnet sind:
$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Durch paarweises Zusammenfassen und anschießendem Sortieren erhält man in fünf Schritten die folgenden Symbolkombinationen (resultierende Wahrscheinlichkeiten in Klammern):
- 1. A (0.30), B (0.24), C (0.20), EF (0.14), D (0.12),
- 2. A (0.30), EFD (0.26), B (0.24), C (0.20),
- 3. BC (0.44), A (0.30), EFD (0.26),
- 4. AEFD (0.56), BC (0.44),
- 5. Root AEFDBC (1.00).
Rückwärts (gemäß den Schritten 5 bis 1) erfolgt dann die Zuordnung zu Binärsymbolen. Ein „x” weist darauf hin, dass in den nächsten Schritten noch Bits hinzugefügt werden müssen:
- 5. AEFD → 1x, BC → 0x,
- 4. A → 11, EFD → 10x,
- 3. B → 01, C → 00,
- 2. EF → 101x, D → 100,
- 1. E → 1011, F → 1010.
Die Unterstreichungen markieren die endgültige Binärcodierung.
Zum Begriff „Entropiecodierung”
Wir gehen weiterhin von den Wahrscheinlichkeiten und Zuordnungen des letzten Beispiels aus:
$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm};$$
$$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 01} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1011} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1010} \hspace{0.05cm}.$$
Von den sechs Quellensymbolen werden also drei mit je zwei Bit, eines mit drei Bit und zwei Symbole ( E und F ) mit vier Bit codiert. Die mittlere Codewortlänge ergibt sich damit zu
$$L_{\rm M} = (0.30 \hspace{-0.05cm}+ \hspace{-0.05cm}0.24 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.20) \cdot 2 + 0.12 \cdot 3 + (0.10 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.04 ) \cdot 4 = 2.4 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Aus dem Vergleich mit der Quellenentropie $H$ = 2.365 bit/Quellensymbol erkennt man die Effizienz der Huffman–Codierung.
Es gibt keinen präfixfreien (⇒ sofort decodierbaren) Code, der allein unter Ausnutzung der Auftrittswahrscheinlichkeiten zu einer kleineren mittleren Codewortlänge führt als der Huffman–Code.
In diesem Sinne ist der Huffman–Code optimal. Wären die Symbolwahrscheinlichkeiten
$$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 1/8 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = p_{\rm F} = 1/16 \hspace{0.05cm},$$
so würde für die Entropie und für die mittlere Codewortlänge gleichermaßen gelten:
$$\begin{align*}H \hspace{-0.15cm}& = \hspace{-0.15cm} 3 \cdot 1/4 \cdot {\rm ld}\hspace{0.1cm}(4) + 1/8 \cdot {\rm ld}\hspace{0.1cm}(8) + 2 \cdot 1/16 \cdot {\rm ld}\hspace{0.1cm}(16) = 2.375 \,{\rm bit/Quellensymbol}\hspace{0.05cm},\\ L_{\rm M} \hspace{-0.15cm}& = \hspace{-0.15cm} 3 \cdot 1/4 \cdot 2 + 1/8 \cdot 3 + 2 \cdot 1/16 \cdot 4 = 2.375 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.\end{align*}$$
Hinweis: Aus Platzgründen ist hier der Logarithmus dualis „log2” mit „ld” bezeichnet. Aus dieser Eigenschaft erklärt sich der Begriff Entropiecodierung. Man versucht bei dieser Form von Quellencodierung, die Länge $L_μ$ der Binärfolge (bestehend aus Nullen und Einsen) für das Symbol $q_μ$ gemäß der Entropieberechnung wie folgt an dessen Auftrittswahrscheinlichkeit $p_μ$ anzupassen:
$$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$
Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ ( $k$ = 1, 2, 3, ... ) dargestellt werden können. In diesem Sonderfall – und nur in diesem – stimmt die mittlere Codewortlänge $L_M$ exakt mit der Quellenentropie $H$ überein (siehe zweites Zahlenbeispiel). Nach dem Quellencodierungstheorem gibt es keinen (decodierbaren) Code, der im Mittel mit weniger Binärzeichen pro Quellensymbol auskommt.
Darstellung des Huffman–Codes als Baumdiagramm
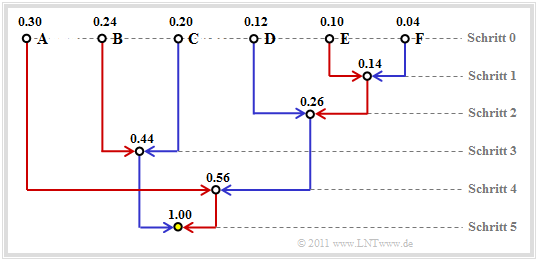
Häufig wird für die Konstruktion des Huffman–Codes eine Baumstruktur verwendet.Für das bisher betrachtete Beispiel zeigt diese die folgende Grafik:
Man erkennt:
- Bei jedem Schritt des Huffman–Algorithmus werden die beiden Zweige mit den jeweils kleinsten Wahrscheinlichkeiten zusammengefasst. Der Knoten im Schritt 1 fasst die zwei Symbole E und F mit den aktuell kleinsten Wahrscheinlichkeiten zusammen. Dieser Knoten ist mit $p_E$ + $p_F$ = 0.14 beschriftet.
- Der vom Symbol mit der kleineren Wahrscheinlichkeit (hier F) zum Summenknoten verlaufende Zweig ist blau eingezeichnet, der andere rot.
Nach fünf Schritten ist man bei der Baumwurzel („Root”) mit der Gesamtwahrscheinlichkeit 1 angelangt. Verfolgt man nun den Verlauf von der Wurzel (in obiger Grafik mit gelber Füllung) zu den einzelnen Symbolen zurück, so kann man aus den Farben der einzelnen Zweige die Symbolzuordnung ablesen. Mit den Zuordnungen „rot” → 1 und „blau” → 0 ergibt sich beispielsweise von der Wurzel zu Symbol
- A: rot, rot → 11,
- B: blau, rot → 01,
- C: blau, blau → 00,
- D: rot, blau, blau → 100,
- E: rot, blau, rot, rot → 1011,
- F: rot, blau, rot, blau → 1010.
Die Zuordnung „rot” → 0 und „blau” → 1 würde ebenfalls zu einem optimalen präfixfreien Huffman–Code führen.
Die folgende Grafik zeigt die Huffman–Codierung von 49 Symbolen $q_ν$ ∈ { A, B, C, D, E, F} mit der auf der letzten Seite hergeleiteten Zuordnung. Die binäre Codesymbolfolge weist die mittlere Codewortlänge $L_M$ = 125/49 = 2.551 auf. Die Farben dienen ausschließlich zur besseren Orientierung.
[[Datei: P_ID2419__Inf_T_2_3_S3b_neu.png|Beispielfolgen bei Huffman–Codierung]]
Aufgrund der kurzen Quellensymbolfolge ( $N$ = 49 ) weichen die Auftrittshäufigkeiten $h_A$, ... , $h_F$ der simulierten Folgen signifikant von den vorgegebenen Wahrscheinlichkeiten $p_A$, ... , $p_F$ ab:
$$\begin{align*}p_{\rm A} \hspace{-0.2cm}& = \hspace{-0.2cm} 0.30 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm A} = 16/49 \approx 0.326 \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm B} = 7/49 \approx 0.143 \hspace{0.05cm},\\ p_{\rm C} \hspace{-0.2cm}& = \hspace{-0.2cm} 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm C}= 9/49 \approx 0.184 \hspace{0.05cm},\hspace{0.6cm}p_{\rm D} = 0.12 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm D} = 7/49 \approx 0.143 \hspace{0.05cm},\\ p_{\rm E} \hspace{-0.2cm}& = \hspace{-0.2cm} 0.10 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm},\hspace{0.6cm}p_{\rm F} = 0.04 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm}.\end{align*}$$
Damit ergibt sich ein etwas größerer Entropiewert:
$$H ({\rm bez\ddot{u}glich }\hspace{0.15cm}p_{\mu}) = 2.365 \,{\rm bit/Quellensymbol}$$
$$\Rightarrow \hspace{0.3cm} H ({\rm bez\ddot{u}glich }\hspace{0.15cm}h_{\mu}) = 2.451 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Würde man den Huffman–Code mit diesen „neuen” Wahrscheinlichkeiten $h_A$, ... , $h_F$ bilden, so ergäben sich folgende Zuordnungen:
$$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 101} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 010} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 011} \hspace{0.05cm}.$$
Nun würden nur A und C mit zwei Bit dargestellt, die anderen vier Symbole durch jeweils drei Bit. Die Codesymbolfolge hätte dann eine Länge von (16 + 9) · 2 + (7 + 7 + 5 + 5) · 3 = 122 Bit, wäre also um drei Bit kürzer als nach der bisherigen Codierung. Die mittlere Codewortlänge wäre dann $L_M$ = 122/49 ≈ 2.49 bit/Quellensymbol anstelle von $L_M$ ≈ 2.55 bit/Quellensymbol. Dieses Beispiel lässt sich wie folgt interpretieren:
- Die Huffman–Codierung lebt von der (genauen) Kenntnis der Symbolwahrscheinlichkeiten. Sind diese sowohl dem Sender als auch dem Empfänger bekannt, so ist die mittlere Codewortlänge $L_M$ oft nur unwesentlich größer als die Quellenentropie $H$.
- Insbesondere bei kleinen Dateien kann es zu Abweichungen zwischen den (erwarteten) Symbolwahrscheinlichkeiten $p_μ$ und den (tatsächlichen) Symbolhäufigkeiten $h_μ$ kommen. Besser wäre es hier, für jede Datei einen eigenen Huffman–Code zu generieren, der auf den tatsächlichen Gegebenheiten ( $h_μ$ ) basiert.
- In diesem Fall muss aber dem Decoder auch der spezifische Huffman–Code mitgeteilt werden. Dies führt zu einem gewissen Overhead, der nur wieder bei längeren Dateien vernachlässigt werden kann. Bei kleinen Dateien lohnt sich dieser Aufwand nicht.
Einfluss von Übertragungsfehlern auf die Decodierung
Der Huffman–Code ist aufgrund der Eigenschaft „präfixfrei” verlustlos. Das bedeutet: Aus der binären Codesymbolfolge lässt sich die Quellensymbolfolge vollständig rekonstruieren. Kommt es aber bei der Übertragung zu einem Fehler (aus einer 0 wird eine 1 bzw. aus einer 1 eine 0), so stimmt natürlich auch die Sinkensymbolfolge $〈υ_ν〉$ nicht mit der Quellensymbolfolge $〈q_ν〉$ überein. Die folgenden Beispiele zeigen, dass ein einziger Übertragungsfehler manchmal eine Vielzahl von Fehlern hinsichtlich des Ursprungstextes zur Folge haben kann.
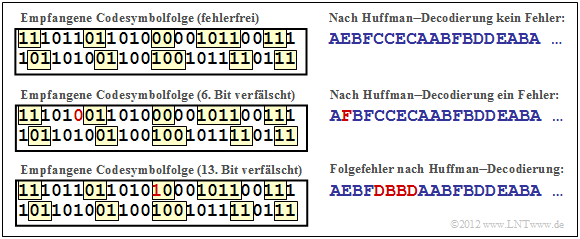
Wir betrachten die gleiche Quellensymbolfolge und den gleichen Huffman–Code wie auf der vorherigen Seite. Die obere Grafik zeigt, dass bei fehlerfreier Übertragung aus der Binärfolge 111011 ... wieder die Folge AEBFCC ... rekonstruiert werden kann.
- Wird aber das 6. Bit verfälscht (von 1 auf 0, rote Markierung in der mittlere Grafik), so wird aus dem Quellensymbol $q_2$ = E das Sinkensymbol $v_2$ = F.
- Eine Verfälschung von Bit 13 (von 0 auf 1, rote Markierung in der unteren Grafik) führt dagegen zu einer Verfälschung von vier Quellensymbolen: CCEC ⇒ DBBD.
Die nächste Seite zeigt ein weiteres Beispiel zum Einfluss von Übertragungsfehlern bei Huffman.
Eine zweite Nachrichtenquelle – ebenfalls mit Symbolumfang $M$ = 6 – ist durch folgende Symbolwahrscheinlichkeiten gekennzeichnet:
$$p_{\rm A} = 0.50 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.19 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.11 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.09 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.06 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.05 \hspace{0.05cm}.$$
Hier führt der Huffman–Algorithmus zu folgender Zuordnung:
$$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 0} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 111} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 101} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1101} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1100} \hspace{0.05cm}.$$
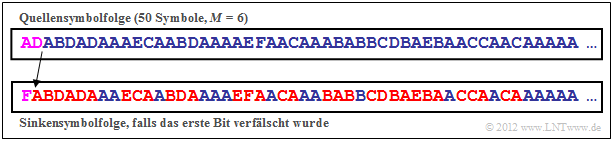
Die Quellensymbolfolge ADABD ... (siehe Grafik) wird somit durch die Codesymbolfolge 0'100'0'111'100' ... dargestellt. Die Hochkommata dienen hierbei nur der Orientierung.
Bei der Übertragung wird nun das erste Bit verfälscht: Anstelle von 01000111100... empfängt man somit 11000111100... Aus den beiden ersten Quellensymbolen AD → 0100 wird dann nach der Decodierung das Sinkensymbol F → 1100. Die weiteren Symbole werden dann wieder richtig detektiert, aber nun nicht mehr beginnend bei $ν$ = 3, sondern bei $ν$ = 2. Je nach Anwendung sind die Auswirkungen unterschiedlich:
- Handelt es sich bei der Quelle um einen natürlichen Text und bei der Sinke um einen Menschen, so bleibt der Großteil des Textes für den Leser verständlich.
- Ist die Sinke jedoch ein Automat, der sukzessive alle $v_ν$ mit den entsprechenden $q_ν$ vergleicht, so ergibt sich eine Verfälschungshäufigkeit von deutlich über 50%.
- Nur die blauen Symbole der Sinkensymbolfolge $〈v_ν〉$ stimmen dann (zufällig) mit den entsprechenden Quellensymbolen überein, während rote Symbole auf Fehler hinweisen.
Anwendung der Huffman–Codierung auf k–Tupel
Der Huffman–Algorithmus in seiner Grundform liefert dann unbefriedigende Ergebnisse, wenn
- eine Binärquelle ( $M$ = 2 ) vorliegt, zum Beispiel mit dem Symbolvorrat {X, Y},
- es statistische Bindungen zwischen den Symbolen der Eingangsfolge gibt,
- die Wahrscheinlichkeit des häufigsten Symbols deutlich größer ist als 50%.
Abhilfe schafft man in diesen Anwendungsfällen, in dem man mehrere Symbole zusammenfasst und den Huffman–Algorithmus auf einen neuen Symbolvorrat {A, B, C, D, ... } anwendet.
Bildet man $k$–Tupel, so steigt der Symbolumfang von $M$ auf $M ′$ = $M^k$. Wir wollen im folgenden Beispiel die Vorgehensweise anhand einer Binärquelle ( $M$ = 2 ) verdeutlichen. Weitere Beispiele finden Sie in Aufgabe A2.7, Aufgabe Z2.7 und Aufgabe A2.8.
Gegeben sei eine gedächtnislose Binärquelle ( $M$ = 2 ) mit den Symbolen {X, Y}:
- Die Symbolwahrscheinlichkeiten seien $p_X$ = 0.8 und $p_Y$ = 0.2.
- Damit ergibt sich die Quellenentropie zu $H$ = 0.722 bit/Quellensymbol.
- Wir betrachten die Symbolfolge XXXYXXXXXXXXYYXXXXXYYXXYXYXXYX ....
Der Huffman–Algorithmus kann auf diese Quelle direkt nicht angewendet werden, das heißt, man benötigt ohne weitere Maßnahme für jedes binäre Quellensymbol auch ein Bit. Aber:
- Fasst man jeweils zwei binäre Symbole zu einem Zweiertupel ( $k$ = 2 ) entsprechend XX → A, XY → B, YX → C, YY → D zusammen, so kann man „Huffman” auf die resultierende Folge ABAACADAABCBBAC ... mit $M′$ = 4 anwenden. Wegen
$$p_{\rm A}= 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 = p_{\rm C} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm D}= 0.2^2 = 0.04$$
erhält man A → 1, B → 00, C → 011, D → 010 sowie
$$L_{\rm M}' = 0.64 \cdot 1 + 0.16 \cdot 2 + 0.16 \cdot 3 + 0.04 \cdot 3 =1.56\,{\rm bit/Zweiertupel} $$
$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{2} = 0.78\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Nun bilden wir Dreiertupel ( $k$ = 3 ). Mit den Kombinationen XXX → A, XXY → B, XYX → C, XYY → D, YXX → E, YXY → F, YYX → G, YYY → H kommt man für die oben angegebene Eingangsfolge zur äquivalenten Folge AEBAGADBCC... (basierend auf dem neuen Symbolumfang $M′$ = 8) und zu folgenden Wahrscheinlichkeiten:
$$\begin{align*}p_{\rm A}\hspace{-0.2cm}& = \hspace{-0.2cm} 0.8^3 = 0.512 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= p_{\rm C}= p_{\rm E} = 0.8^2 \cdot 0.2 = 0.128\hspace{0.05cm},\\ p_{\rm D}\hspace{-0.2cm}& = \hspace{-0.2cm} p_{\rm F}= p_{\rm G} = 0.8 \cdot 0.2^2 = 0.032 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm H}= 0.2^3 = 0.008\hspace{0.05cm}. \end{align*}$$
Die Huffman–Codierung lautet somit: A → 1, B → 011, C → 010, D → 00011, E → 001, F → 00010, G → 00001, H → 00000. Damit erhält man für die mittlere Codewortlänge:
$$L_{\rm M}' = 0.512 \cdot 1 + 3 \cdot 0.128 \cdot 3 + (3 \cdot 0.032 + 0.008) \cdot 5 =2.184 \,{\rm bit/Dreiertupel} $$
$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{3} = 0.728\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
Bereits mit $k$ = 3 wird also in diesem Beispiel die Quellenentropie $H$ = 0.722 fast erreicht.