Digitalsignalübertragung/Trägerfrequenzsysteme mit nichtkohärenter Demodulation: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{Header |Untermenü=Verallgemeinerte Beschreibung digitaler Modulationsverfahren |Vorherige Seite=Trägerfrequenzsysteme mit kohärenter Demodulation |Näch…“) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 33: | Zeile 33: | ||
[[Datei:P ID2082 Dig T 4 5 S1 version1.png|Rayleigh- und Rice-WDF|class=fit]]<br> | [[Datei:P ID2082 Dig T 4 5 S1 version1.png|Rayleigh- und Rice-WDF|class=fit]]<br> | ||
| + | == Rayleigh– und Riceverteilung (2) == | ||
| + | <br> | ||
| + | Die Grafik am Seitenende zeigt nochmals die Wahrscheinlichkeitsdichtefunktionen von Rayleigh– und Riceverteilung. Zu dieser Darstellung ist anzumerken: | ||
| + | *Die [http://www.lntwww.de/Stochastische_Signaltheorie/Weitere_Verteilungen#Riceverteilung Riceverteilung] ist durch die beiden Parameter <i>C</i> und <i>σ<sub>n</sub></i> bestimmt. Mit <i>C</i> = 0 ist die Rice–WDF identisch mit der [http://www.lntwww.de/Stochastische_Signaltheorie/Weitere_Verteilungen#Rayleighverteilung Rayleigh–WDF].<br> | ||
| + | *Die Rayleigh–WDF mit größerem <i>σ<sub>n</sub></i> ist formgleich mit der gezeichneten Kurve (<i>σ<sub>n</sub></i> = 0.5), jedoch im Verhältnis der Streuungen breiter und niedriger.<br> | ||
| + | |||
| + | *<i>σ<sub>n</sub></i> gibt die Streuungen der beiden gaußverteilten Zufallsgrößen <i>u</i> und <i>υ</i> an (beide haben gleiche Streuung) und nicht die Streuung der rayleighverteilten Zufallsgröße <i>y</i>. Für diese gilt vielmehr: | ||
| + | |||
| + | ::<math>\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Die Rayleighverteilung ist extrem unsymmetrisch, erkennbar am (relativ) großen Wert für das [http://www.lntwww.de/Stochastische_Signaltheorie/Erwartungswerte_und_Momente#Zentralmomente Zentralmoment 3. Ordnung:] <i>μ</i><sub>3</sub>/<i>σ<sub>y</sub></i><sup>3</sup> ≈ 0.27.<br> | ||
| + | |||
| + | *Die Riceverteilung ist um so symmetrischer, je größer das Verhältnis <i>C</i>/<i>σ<sub>n</sub></i> von deterministischer und stochastischer Komponente ist. Für <i>C</i>/<i>σ<sub>n</sub></i> ≥ 4 ist <i>μ</i><sub>3</sub> nahezu 0.<br> | ||
| + | |||
| + | *Weiterhin ist zu erkennen, dass sich die Riceverteilung (mit den Parametern <i>C</i> und <i>σ<sub>n</sub></i>) immer mehr einer Gaußverteilung mit Mittelwert <i>C</i> und Streuung <i>σ<sub>n</sub></i> annähert, je größer der Quotient <i>C</i>/<i>σ<sub>n</sub></i> ist: | ||
| + | |||
| + | ::<math>p_y (\eta) \approx \frac{1}{\sqrt{2\pi} \cdot \sigma_n} | ||
| + | \cdot {\rm exp } \left [ - \frac{(\eta - C)^2}{2 \sigma_n^2}\right ] | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} m_y = C\hspace{0.05cm},\hspace{0.2cm}\sigma_y = \sigma_n | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | [[Datei:P ID2086 Dig T 4 5 S1 version1.png|Rayleigh– und Rice–WDF|class=fit]]<br> | ||
{{Display}} | {{Display}} | ||
Version vom 28. Dezember 2016, 22:00 Uhr
Rayleigh– und Riceverteilung (1)
Die für eine kohärente Demodulation erforderliche Schätzung des Phasenwinkels aus dem ankommenden Signal ist bei vielen Anwendungen nicht oder nur eingeschränkt möglich. So führt die Bewegung eines Mobilteilnehmers mit hoher Geschwindigkeit zu sehr schnellen zeitlichen Änderungen des Phasenwinkels ϕ, was dessen ausreichend genaue Bestimmung erschwert oder gar verhindert.
Diese Tatsache führt zu den nichtkohärenten Demodulationsverfahren mit dem Vorteil reduzierter Komplexität, allerdings mit erhöhter Verfälschungswahrscheinlichkeit. Bei der Herleitung der Gleichungen stößt man auf zwei Wahrscheinlichkeitsdichtefunktionen, die hier vorneweg angegeben werden:
- Die Rayleighverteilung erhält man für die WDF der Zufallsgröße y mit Realisierung η, die sich aus den beiden gaußverteilten und statistisch unabhängigen Komponenten u und υ (beide mit der gleichen Streuung σn) wie folgt ergibt:
- \[y = \sqrt{u^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) ={\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - {\eta^2}/{ (2\sigma_n^2)}\right ] \hspace{0.05cm}.\]
- Die Riceverteilung erhält man unter sonst gleichen Randbedingungen für den Fall, dass bei einer der Komponenten (entweder u oder υ) noch eine Konstante C addiert wird:
- \[y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = {\eta}/{\sigma_n^2} \cdot {\rm exp } \left [ - ({\eta^2 + C^2})/(2 \sigma_n^2) \right ] \cdot {\rm I }_0 \left [{\eta \cdot C}/{ \sigma_n^2}\right ] \hspace{0.05cm}.\]
Für die Riceverteilung benötigt man die modifizierte Besselfunktion nullter Ordnung, deren Definition und Reihenentwicklung wie folgt lauten:
\[{\rm I }_0 (x) = \frac{1}{ 2\pi} \cdot \int_{0}^{2\pi} {\rm e }^{-x \hspace{0.03cm}\cdot \hspace{0.03cm}\cos(\alpha)} \,{\rm d} \alpha \hspace{0.2cm} \approx \hspace{0.2cm} \sum_{k = 0}^{\infty} \frac{(x/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
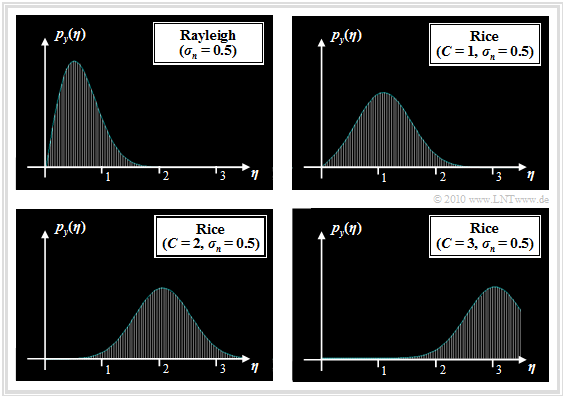
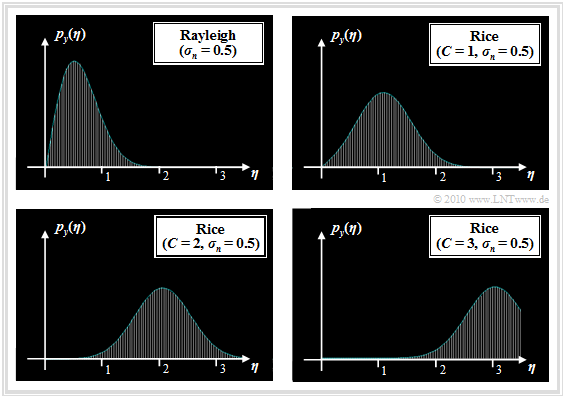
Die Grafik zeigt Rayleigh– und Rice–Wahrscheinlichkeitsdichtefunktionen. Die Bildbeschreibung folgt auf der nächsten Seite.
Rayleigh– und Riceverteilung (2)
Die Grafik am Seitenende zeigt nochmals die Wahrscheinlichkeitsdichtefunktionen von Rayleigh– und Riceverteilung. Zu dieser Darstellung ist anzumerken:
- Die Riceverteilung ist durch die beiden Parameter C und σn bestimmt. Mit C = 0 ist die Rice–WDF identisch mit der Rayleigh–WDF.
- Die Rayleigh–WDF mit größerem σn ist formgleich mit der gezeichneten Kurve (σn = 0.5), jedoch im Verhältnis der Streuungen breiter und niedriger.
- σn gibt die Streuungen der beiden gaußverteilten Zufallsgrößen u und υ an (beide haben gleiche Streuung) und nicht die Streuung der rayleighverteilten Zufallsgröße y. Für diese gilt vielmehr:
- \[\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n \hspace{0.05cm}.\]
- Die Rayleighverteilung ist extrem unsymmetrisch, erkennbar am (relativ) großen Wert für das Zentralmoment 3. Ordnung: μ3/σy3 ≈ 0.27.
- Die Riceverteilung ist um so symmetrischer, je größer das Verhältnis C/σn von deterministischer und stochastischer Komponente ist. Für C/σn ≥ 4 ist μ3 nahezu 0.
- Weiterhin ist zu erkennen, dass sich die Riceverteilung (mit den Parametern C und σn) immer mehr einer Gaußverteilung mit Mittelwert C und Streuung σn annähert, je größer der Quotient C/σn ist:
- \[p_y (\eta) \approx \frac{1}{\sqrt{2\pi} \cdot \sigma_n} \cdot {\rm exp } \left [ - \frac{(\eta - C)^2}{2 \sigma_n^2}\right ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} m_y = C\hspace{0.05cm},\hspace{0.2cm}\sigma_y = \sigma_n \hspace{0.05cm}.\]