Digitalsignalübertragung/Signale, Basisfunktionen und Vektorräume: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
Ayush (Diskussion | Beiträge) |
||
| Zeile 116: | Zeile 116: | ||
:<math>\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.2cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.2cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.</math>{{end}}<br> | :<math>\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.2cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.2cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.</math>{{end}}<br> | ||
| + | == Das Verfahren nach Gram-Schmidt (1) == | ||
| + | <br> | ||
| + | Im Beispiel auf der letzten Seite war die Angabe der beiden orthonormalen Basisfunktionen <i>φ</i><sub>1</sub>(<i>t</i>) und <i>φ</i><sub>2</sub>(<i>t</i>) sehr einfach, da diese formgleich mit <i>s</i><sub>1</sub>(<i>t</i>) und <i>s</i><sub>2</sub>(<i>t</i>) waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen <i>φ</i><sub>1</sub>(<i>t</i>), ... , <i>φ<sub>N</sub></i>(<i>t</i>) für beliebig vorgebbare Signale <i>s</i><sub>1</sub>(<i>t</i>), ... , <i>s<sub>M</sub></i>(<i>t</i>), und zwar wie folgt: | ||
| + | *Die erste Basisfunktion <i>φ</i><sub>1</sub>(<i>t</i>) ist formgleich mit <i>s</i><sub>1</sub>(<i>t</i>). Es gilt: | ||
| + | ::<math>\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 | ||
| + | \hspace{0.05cm}.</math> | ||
| + | *Es wird nun angenommen, dass aus den Signalen <i>s</i><sub>1</sub>(<i>t</i>), ... , <i>s</i><sub><i>k</i>–1</sub>(<i>t</i>) bereits die Basisfunktionen <i>φ</i><sub>1</sub>(<i>t</i>), ... , <i>φ</i><sub><i>n</i>–1</sub>(<i>t</i>) berechnet wurden (<i>n</i> ≤ <i>k</i>). Dann berechnen wir mittels <i>s<sub>k</sub></i>(<i>t</i>) die Hilfsfunktion | ||
| + | ::<math>\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} | ||
| + | s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, ... \hspace{0.1cm}, n-1\hspace{0.05cm}.</math> | ||
| + | |||
| + | *Ist <i>θ<sub>k</sub></i>(<i>t</i>) ≡ 0 ⇒ ||<i>θ<sub>k</sub></i>(<i>t</i>)|| = 0, so liefert <i>s<sub>k</sub></i>(<i>t</i>) keine neue Basisfunktion. Vielmehr lässt sich dann <i>s<sub>k</sub></i>(<i>t</i>) durch die <i>n</i>–1 bereits vorher gefundenen Basisfunktionen <i>φ</i><sub>1</sub></i>(<i>t</i>), ... , <i>φ</i><sub><i>n</i>–1</sub>(<i>t</i>) ausdrücken: | ||
| + | |||
| + | ::<math>s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.</math> | ||
| + | |||
| + | *Eine neue Basisfunktion (nämlich die <i>n</i>–te) ergibt sich, falls ||<i>θ<sub>k</sub></i>(<i>t</i>)|| ≠ 0 ist: | ||
| + | |||
| + | ::<math>\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.</math> | ||
| + | |||
| + | Diese Prozedur kann fortgesetzt werden, bis alle <i>M</i> Signale berücksichtigt wurden. Danach hat man alle <i>N</i> ≤ <i>M</i> orthonormalen Basisfunktionen <i>φ<sub>j</sub></i>(<i>t</i>) gefunden. Der Sonderfall <i>N</i> = <i>M</i> ergibt sich nur dann, wenn alle <i>M</i> Signale linear voneinander unabhängig sind.<br> | ||
| + | |||
| + | Auf der nächsten Seite wird das Gram–Schmidt–Verfahren an einem einfachen Beispiel verdeutlicht. Wir verweisen auch auf das folgende Interaktionsmodul:<br> | ||
| + | |||
| + | [[:File:gram-schmidt.swf|Gram–Schmidt–Verfahren]]<br> | ||
Version vom 28. Dezember 2016, 00:25 Uhr
Inhaltsverzeichnis
Zur Nomenklatur im vierten Kapitel (1)
Nahezu alle Ergebnisse dieses Kapitels wurden bereits in früheren Abschnitten hergeleitet. Grundlegend neu ist jedoch die Herangehensweise:
- Im Buch „Modulationsverfahren” sowie in den ersten drei Kapiteln dieses Buches wurden bereits bei den Herleitungen die spezifischen Systemeigenschaften berücksichtigt – zum Beispiel, ob die Übertragung des Digitalsignals im Basisband erfolgt oder ob eine digitale Amplituden–, Frequenz– oder Phasenmodulation vorliegt.
- Hier sollen nun die Systeme dahingehend abstrahiert werden, dass sie einheitlich behandelt werden können. Der jeweils optimale Empfänger besitzt in allen Fällen die gleiche Struktur, und die Fehlerwahrscheinlichkeit lässt sich auch für nichtgaußverteiltes Rauschen angeben.
Anzumerken ist, dass sich durch diese eher globale Vorgehensweise gewisse Systemunzulänglichkeiten nicht oder nur sehr ungenau erfassen lassen, wie beispielsweise
- der Einfluss eines nichtoptimalen Empfangsfilters auf die Fehlerwahrscheinlichkeit,
- ein falscher Schwellenwert (Schwellendrift) oder
- Phasenjitter (Schwankungen der Abtastzeitpunkte).
Insbesondere bei Vorhandensein von Impulsinterferenzen sollte also weiterhin entsprechend Kapitel 3 vorgegangen werden.
Die Beschreibung basiert auf dem Skript Kötter, R., Zeitler, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008 von Ralf Kötter und Georg Zeitler, das sich stark an das Buch Wozencraft, J. M.; Jacobs, I. M.: Principles of Communication Engineering. New York: John Wiley & Sons, 1965 anlehnt. Gerhard Kramer, Lehrstuhlinhaber des LNT seit 2010, behandelt in seiner NT2–Vorlesung Kramer, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2010 die gleiche Thematik mit sehr ähnlicher Nomenklatur.
Um unseren eigenen Studenten an der TU München das Lesen nicht unnötig zu erschweren, halten wir uns weitestgehend an diese Nomenklatur, auch wenn diese von anderen LNTwww–Kapiteln abweicht.
Zur Nomenklatur im vierten Kapitel (2)
Gegenüber den anderen Kapiteln in LNTwww ergeben sich hier folgende Nomenklaturunterschiede:
- Die zu übertragende Nachrich ist ein ganzzahliger Wert m ∈ {mi} mit i = 0, ... , M – 1, wobei M den Symbolumfang angibt. Wenn es die Beschreibung vereinfacht, wird i = 1, ... , M induziert.
- Das Ergebnis des Entscheidungsprozesses beim Empfänger ist ebenfalls ein Integerwert mit dem gleichen Symbolalphabet wie beim Sender. Man bezeichnet dieses Ergebnis auch als Schätzwert:
- \[\hat{m} \in \{m_i \}, \hspace{0.2cm} i = 0, 1, ...\hspace{0.05cm} , M-1\hspace{0.2cm} ({\rm bzw.}\,\,i = 1, 2, ... \hspace{0.05cm}, M) \hspace{0.05cm}.\]
- Die Symbolfehlerwahrscheinlichkeit wird meist wie folgt bezeichnet:
- \[{\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) = 1 - {\rm Pr} ({\cal C}), \hspace{0.4cm}{\rm Komplement\ddot{a}rereignis\hspace{-0.1cm}:}\hspace{0.2cm} {\rm Pr} ({\cal C}) = {\rm Pr} ( \hat{m} = m) \hspace{0.05cm}.\]
- Im Fließtext wird aufgrund des durch HTML eingeschränkten Zeichensatzes „Pr(Symbolfehler)” oder auch „pS” verwendet.
- Bei einer Wahrscheinlichkeitsdichtefunktion (WDF) wird nun entsprechend pr(ρ) zwischen der Zufallsgröße (r) und der Realisierung (ρ) unterschieden. Bisher wurde für eine WDF die Bezeichnung „fr(r)” verwendet – siehe Kapitel 3.1 im Buch „Stochastische Signaltheorie”.
- Mit der Schreibweise pr(ρ) geben r und ρ Skalare an. Sind dagegen Zufallsgröße und Realisierung Vektoren (geeigneter Länge), so wird dies durch Fettschrift ausgedrückt:
- \[p_{ \boldsymbol{ r}}(\boldsymbol{\rho}){\rm \hspace{0.15cm}mit \hspace{0.15cm}den \hspace{0.15cm}Vektoren\hspace{0.15cm}} \boldsymbol{ r}{\rm \hspace{0.15cm}und\hspace{0.15cm}}\boldsymbol{\rho}.\hspace{0.05cm}\]
- Um Verwechslungen mit Energiewerten zu vermeiden, heißt nun der Schwellenwert G anstelle von E und wird in diesem Kapitel vorwiegend als Entscheidungsgrenze bezeichnet.
- Ausgehend von den beiden reellen und energiebegrenzten Zeitfunktionen x(t) und y(t) erhält man für das innere Produkt
- \[<\hspace{-0.1cm}x(t), \hspace{0.05cm}y(t) \hspace{-0.1cm}> \hspace{0.15cm}= \int_{-\infty}^{+\infty}x(t) \cdot y(t)\,d \it t \hspace{0.05cm},\]
- und für die 2–Norm (oder kurz Norm):
- \[||x(t) || = \sqrt{<\hspace{-0.1cm}x(t), \hspace{0.05cm}x(t) \hspace{-0.1cm}>} \hspace{0.05cm}.\]
Gegenüber dem Skript Kötter, R., Zeitler, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008 unterscheidet sich die Bezeichnungsweise hier wie folgt:
- Die Wahrscheinlichkeit des Ereignisses „E” ist Pr(„E”); in Kötter, R., Zeitler, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008 wird hier P(„E”) verwendet. Diese Nomenklaturänderung wurde auch deshalb vorgenommen, da Wahrscheinlichkeiten und Leistungen in manchen Gleichungen gemeinsam vorkommen.
- Bandpass–Signale werden weiterhin mit Index „BP” gekennzeichnet und nicht wie in Kötter, R., Zeitler, G.: Nachrichtentechnik 2. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2008 mit einer Tilde. Das entsprechende Tiefpass–Signal ist (meist) mit dem Index „TP” versehen.
Orthonormale Basisfunktionen (1)
Wir gehen in diesem Kapitel von einem Satz {si(t)} möglicher Sendesignale aus, die den möglichen Nachrichten mi eineindeutig zugeordnet werden können. Mit i = 1, ... , M gilt:
\[m \in \{m_i \}, \hspace{0.2cm} s(t) \in \{s_i(t) \}\hspace{-0.1cm}: m = m_i \hspace{0.1cm} \Leftrightarrow \hspace{0.1cm} s(t) = s_i(t) \hspace{0.05cm}.\]
Weiter setzen wir für das Folgende voraus, dass die M Signale si(t) energiebegrenzt sind, was meist gleichzeitig bedeutet, dass sie nur von endlicher Dauer sind.
\[s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t) , \hspace{0.3cm}i = 1,\hspace{0.05cm} ...\hspace{0.1cm} , M, \hspace{0.3cm}j = 1,\hspace{0.05cm} ... \hspace{0.1cm}, N \hspace{0.05cm}.\]
Jeweils zwei Basisfunktionen φj(t) und φk(t) müssen orthonormal zueinander sein, das heißt, es muss gelten (δjk nennt man das Kronecker–Symbol):
\[<\hspace{-0.1cm}\varphi_j(t), \hspace{0.05cm}\varphi_k(t) \hspace{-0.1cm}> = \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\,d \it t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.1cm}j = k \\ {\rm falls}\hspace{0.1cm} j \ne k \\ \end{array} \hspace{0.05cm}.\]
Der Parameter N gibt dabei an, wieviele Basisfunktionen φj(t) benötigt werden, um die M möglichen Sendesignale darzustellen. Mit anderen Worten: N ist die Dimension des Vektorraums, der von den M Signalen aufgespannt wird. Dabei gilt:
- Ist N = M, so sind alle Sendesignale zueinander orthogonal. Sie sind nicht notwendigerweise orthonormal, das heißt, die Energien Ei = 〈si(t), si(t)〉 können durchaus ungleich 1 sein.
- N < M ergibt sich, wenn mindestens ein Signal si(t) als Linearkombination von Basisfunktionen φj(t) dargestellt werden kann, die sich aus anderen Signalen sj(t) ≠ si(t) ergeben haben.
Orthonormale Basisfunktionen (2)
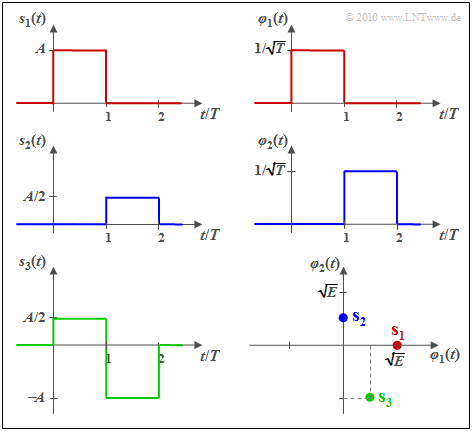
- s1(t) und s2(t) zueinander orthogonal sind,
- die Energie E1 = A2 · T = E ist und E2 = E/4 gilt,
- φ1(t) und φ2(t) jeweils formgleich mit s1(t) bzw. s2(t) sind und beide die Energie 1 besitzen:
- \[\varphi_1(t) \hspace{-0.15cm} = \hspace{-0.15cm}\frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{\sqrt{A^2 \cdot T}} = \frac{1}{\sqrt{ T}} \cdot \frac{s_1(t)}{A}\hspace{0.95cm}\Rightarrow \hspace{0.1cm}s_1(t) = s_{11} \cdot \varphi_1(t)\hspace{0.05cm},\hspace{0.1cm}s_{11} = \sqrt{E}\hspace{0.05cm},\]
- \[\varphi_2(t) \hspace{-0.15cm} = \hspace{-0.15cm}\frac{s_2(t)}{\sqrt{E_2}} = \frac{s_2(t)}{\sqrt{(A/2)^2 \cdot T}} = \frac{1}{\sqrt{ T}} \cdot \frac{s_2(t)}{A/2}\hspace{0.05cm}\hspace{0.1cm}\Rightarrow \hspace{0.1cm}s_2(t) = s_{21} \cdot \varphi_2(t)\hspace{0.05cm},\hspace{0.1cm}s_{21} = \frac{\sqrt{E}}{2}\hspace{0.05cm}.\]
- s3(t) durch die Basisfunktionen φ1(t) und φ2(t) ausgedrückt werden kann:
- \[s_3(t) \hspace{-0.1cm} = \hspace{-0.1cm}s_{31} \cdot \varphi_1(t) + s_{32} \cdot \varphi_2(t)\hspace{0.05cm},\]
- \[s_{31} \hspace{-0.1cm} = \hspace{-0.1cm} {A}/{2} \cdot \sqrt {T}= {\sqrt{E}}/{2}\hspace{0.05cm}, \hspace{0.2cm}s_{32} = - A \cdot \sqrt {T} = -\sqrt{E} \hspace{0.05cm}.\]
Im rechten unteren Bild sind die Signale in einer 2D–Darstellung mit den Basisfunktionen φ1(t) und φ2(t) als Achsen dargestellt, wobei E = A2 · T gilt und der Zusammenhang zu den anderen Grafiken durch die Farbgebung zu erkennen ist. Die vektoriellen Repräsentanten der Signale s1(t), s2(t) und s3(t) in diesem zweidimensionellen Vektorraum lassen sich daraus wie folgt ablesen:
\[\mathbf{s}_1 = (\sqrt{ E}, \hspace{0.1cm}0), \hspace{0.2cm} \mathbf{s}_2 = (0, \hspace{0.1cm}\sqrt{ E}/2), \hspace{0.2cm} \mathbf{s}_3 = (\sqrt{ E}/2,\hspace{0.1cm}-\sqrt{ E} ) \hspace{0.05cm}.\]
Das Verfahren nach Gram-Schmidt (1)
Im Beispiel auf der letzten Seite war die Angabe der beiden orthonormalen Basisfunktionen φ1(t) und φ2(t) sehr einfach, da diese formgleich mit s1(t) und s2(t) waren. Das Gram–Schmidt–Verfahren findet die Basisfunktionen φ1(t), ... , φN(t) für beliebig vorgebbare Signale s1(t), ... , sM(t), und zwar wie folgt:
- Die erste Basisfunktion φ1(t) ist formgleich mit s1(t). Es gilt:
- \[\varphi_1(t) = \frac{s_1(t)}{\sqrt{E_1}} = \frac{s_1(t)}{|| s_1(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_1(t) || = 1, \hspace{0.2cm}s_{11} =|| s_1(t)||,\hspace{0.2cm}s_{1j} = 0 \hspace{0.2cm}{\rm f{\rm \ddot{u}r }}\hspace{0.2cm} j \ge 2 \hspace{0.05cm}.\]
- Es wird nun angenommen, dass aus den Signalen s1(t), ... , sk–1(t) bereits die Basisfunktionen φ1(t), ... , φn–1(t) berechnet wurden (n ≤ k). Dann berechnen wir mittels sk(t) die Hilfsfunktion
- \[\theta_k(t) = s_k(t) - \sum\limits_{j = 1}^{n-1}s_{kj} \cdot \varphi_j(t) \hspace{0.4cm}{\rm mit}\hspace{0.4cm} s_{kj} = \hspace{0.1cm} < \hspace{-0.1cm} s_k(t), \hspace{0.05cm}\varphi_j(t) \hspace{-0.1cm} >, \hspace{0.2cm} j = 1, ... \hspace{0.1cm}, n-1\hspace{0.05cm}.\]
- Ist θk(t) ≡ 0 ⇒ ||θk(t)|| = 0, so liefert sk(t) keine neue Basisfunktion. Vielmehr lässt sich dann sk(t) durch die n–1 bereits vorher gefundenen Basisfunktionen φ1(t), ... , φn–1(t) ausdrücken:
- \[s_k(t) = \sum\limits_{j = 1}^{n-1}s_{kj}\cdot \varphi_j(t) \hspace{0.05cm}.\]
- Eine neue Basisfunktion (nämlich die n–te) ergibt sich, falls ||θk(t)|| ≠ 0 ist:
- \[\varphi_n(t) = \frac{\theta_k(t)}{|| \theta_k(t)||} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} || \varphi_n(t) || = 1\hspace{0.05cm}.\]
Diese Prozedur kann fortgesetzt werden, bis alle M Signale berücksichtigt wurden. Danach hat man alle N ≤ M orthonormalen Basisfunktionen φj(t) gefunden. Der Sonderfall N = M ergibt sich nur dann, wenn alle M Signale linear voneinander unabhängig sind.
Auf der nächsten Seite wird das Gram–Schmidt–Verfahren an einem einfachen Beispiel verdeutlicht. Wir verweisen auch auf das folgende Interaktionsmodul: