Digitalsignalübertragung/Anwendungen bei Multimedia–Dateien: Unterschied zwischen den Versionen
| Zeile 127: | Zeile 127: | ||
Wir demonstrieren zunächst den Einfluss von Übertragungsfehlern auf die Audiodatei „Stille.wav” mit ca. 10 Sekunden Dauer. Das heißt: Alles, was Sie hören, sind Übertragungsfehler. | Wir demonstrieren zunächst den Einfluss von Übertragungsfehlern auf die Audiodatei „Stille.wav” mit ca. 10 Sekunden Dauer. Das heißt: Alles, was Sie hören, sind Übertragungsfehler. | ||
| + | |||
'''Statistisch unabhängige Fehler entsprechend dem BSC–Modell''' | '''Statistisch unabhängige Fehler entsprechend dem BSC–Modell''' | ||
| Zeile 138: | Zeile 139: | ||
<lntmedia>file:A_ID45__ruhe1_bsc_01.mp3</lntmedia> $p=10^{-2}$ ⇒ Warnung vor dem Öffnen.<br><br> | <lntmedia>file:A_ID45__ruhe1_bsc_01.mp3</lntmedia> $p=10^{-2}$ ⇒ Warnung vor dem Öffnen.<br><br> | ||
<lntmedia>file:A_ID46__ruhe1_bsc_1.mp3</lntmedia> $p=10^{-1}$ ⇒ Nur für extrem Lärmunempfindliche geeignet.<br><br> | <lntmedia>file:A_ID46__ruhe1_bsc_1.mp3</lntmedia> $p=10^{-1}$ ⇒ Nur für extrem Lärmunempfindliche geeignet.<br><br> | ||
| − | |||
'''Gegenüberstellung von statistisch unabhängigen Fehlern und Bündelfehlern''' | '''Gegenüberstellung von statistisch unabhängigen Fehlern und Bündelfehlern''' | ||
| Zeile 146: | Zeile 146: | ||
*Die mittlere Fehlerwahrscheinlichkeit beträgt auch hier $p_{\rm M}=10^{-3}$. | *Die mittlere Fehlerwahrscheinlichkeit beträgt auch hier $p_{\rm M}=10^{-3}$. | ||
*Gegenübergestellt wird die sehr kurze [[Digitalsignalübertragung/Bündelfehlerkanäle#Fehlerkorrelationsfunktion_des_GE.E2.80.93Modells|Korrelationsdauer]] $D_{\rm K}= 8$ mit weitweichenden statistischen Bindungen ⇒ $D_{\rm K}= 1000$. | *Gegenübergestellt wird die sehr kurze [[Digitalsignalübertragung/Bündelfehlerkanäle#Fehlerkorrelationsfunktion_des_GE.E2.80.93Modells|Korrelationsdauer]] $D_{\rm K}= 8$ mit weitweichenden statistischen Bindungen ⇒ $D_{\rm K}= 1000$. | ||
| + | |||
Zunächst gehen wir wieder von der Datei „Stille.wav” aus. Man erkennt, dass eine kurze Fehlerkorrelationsdauer des GE–Modells im Ergebnis sich nicht allzu sehr von statistisch unabhängigen Fehlern unterscheidet, da jeder Abtastwert mit 16 Bit dargestellt wird. '''Was ist mit''' $D_{\rm K}= 1000$? | Zunächst gehen wir wieder von der Datei „Stille.wav” aus. Man erkennt, dass eine kurze Fehlerkorrelationsdauer des GE–Modells im Ergebnis sich nicht allzu sehr von statistisch unabhängigen Fehlern unterscheidet, da jeder Abtastwert mit 16 Bit dargestellt wird. '''Was ist mit''' $D_{\rm K}= 1000$? | ||
| Zeile 153: | Zeile 154: | ||
<lntmedia>file:A_ID52__ruhe1_ge_1000.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 1000$.<br><br> | <lntmedia>file:A_ID52__ruhe1_ge_1000.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 1000$.<br><br> | ||
| − | Auch beim nachfolgenden kurzen Musikstück gelten die gleichen Kanalparameter.<br> | + | Auch beim nachfolgenden kurzen Musikstück gelten die gleichen Kanalparameter und man erkennt ähnliche Eigenschaften.<br> |
<lntmedia>file:A_ID48__k2_bsc.mp3</lntmedia> BSC–Modell. <br><br> | <lntmedia>file:A_ID48__k2_bsc.mp3</lntmedia> BSC–Modell. <br><br> | ||
<lntmedia>file:A_ID53__k2_ge_8.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 8$. <br><br> | <lntmedia>file:A_ID53__k2_ge_8.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 8$. <br><br> | ||
<lntmedia>file:A_ID54__k2_ge_1000.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 1000$.<br><br> | <lntmedia>file:A_ID54__k2_ge_1000.mp3</lntmedia> GE–Modell mit $D_{\rm K}= 1000$.<br><br> | ||
| + | |||
| + | ''Hinweis'': Alle BMP–Bilder und WAV–Audios zu diesem Kapitel wurden mit dem Windows–Programm „Digitale Kanalmodelle & Multimedia” aus dem (früheren) Praktikum „Simulation Digitaler Übertragungssysteme ” am Lehrstuhl für Nachrichtentechnik der TU München erzeugt. Die folgenden Links stellen bereit: | ||
| + | *das Windows-Programm [http://www.lntwww.de/downloads/Sonstiges/Programme/DKM.zip DKM] ⇒ Link verweist auf die ZIP-Version des Programms; und | ||
| + | *die zugehörige [http://www.lntwww.de/downloads/Sonstiges/Texte/Digitale_Kanalmodelle.pdf Praktikumsanleitung] ⇒ Link verweist auf die PDF-Version. | ||
Version vom 10. Oktober 2017, 10:04 Uhr
Inhaltsverzeichnis
Bilder im BMP–Format
Eines der ältesten Bildformate ist das so genannte Bitmap–Format. Entsprechende Dateien werden mit der Endung „bmp” gekennzeichnet. Wesentliche Eigenschaften von BMP–Bildern sind:
- Unter einer Bitmap versteht man eine Matrix von Bildpunkten, deren einzelne Elemente auch als Pixel (Picture Elements) bezeichnet werden. Abgespeichert werden die Bildpunkte zeilenweise, jeweils von rechts unten nach links oben.
- Jedes Pixel bekommt noch einen RGB–Farbwert aus den additiven Grundfarben „Rot”, „Grün” und „Blau”zugewiesen. Je größer der Farbwert sein kann, desto feiner können die darzustellenden Farben abgestuft werden.
- Die Farbtiefe eines Bildes wird in Bits per Pixel (BPP) angegeben. Gängig sind Farbtiefen von 1 (Schwarzweißbild), 4, 8 und 24 (Echtfarbbild, True Color).
- Da die meisten Bilder nicht das gesamte Farbenspektrum ausnutzen, kann man in jeder Bitmap eine spezifische Zuordnung in Form einer Farbtabelle definieren. So lassen sich auch mit relativ geringer Farbtiefe (bis zu 8 Bit) die Bilder mit guter Farbqualität darstellen.
Eine jede BMP–Datei besteht aus drei Teilblöcken, wie die nebenstehende Grafik beispielhaft verdeutlicht:
- dem Dateikopf (14 Byte),
- dem Informationsblock (mindestens 40 Byte), und anschließend
- dem Bilddatenblock
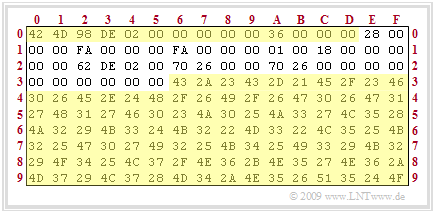
Dargestellt sind die ersten 160 Byte der Datei „LNTprofs.bmp”. Gelb hinterlegt sind sowohl der Dateikopf (in Hexadezimaldarstellung von 0x00 bis 0x0D) als auch der Bilddatenbereich (ab 0x36). Nicht hinterlegt ist der 40 Byte–Informationsblock (von 0x0E bis 0x35).
Der Dateikopf beinhaltet folgende Informationen (der Präfix „0x” zeigt die Hexadezimaldarstellung an und das nachgestellte „d” weist auf die Dezimaldarstellung hin):
- 0x00 ... 0x01 (2 Byte) BMP–Kennung: 0x 42 4D ⇒ „BM”,
- 0x02 ... 0x05 (4 Byte) Dateigröße in Byte: 0x 02 DE 98 ⇒ 188056d,
- 0x06 ... 0x09 (5 Byte) reserviert (muss immer mit Nullen belegt sein),
- 0x0A ... 0x0D (4 Byte) Offset (Beginn der Bilddaten): 0x 00 00 00 36 ⇒ 54d.
Hinweis: Diese Angaben gelten allerdings nur für den Intel–Prozessor, der nach der so genannten Little–Endian–Byteanordnung vom niederwertigsten Byte (englisch: Least Significant Byte, LSB) zum höchstwertigen Byte (englisch: Most Significant Byte, MSB) Byte liest. Die Anordnung „98 DE 02 00” der Bytes 2, ..., 5 ist somit als „0x 00 02 DE 98” zu interpretieren, was der Dezimalzahl „188056” entspricht.
Der 40 Byte–Informationsblock beinhaltet folgende Werte (Bytes mit dem Inhalt „00” sind hier nicht angegeben):
- 0x0E ... 0x11 (4 Byte) Länge des Info–Blocks: 0x 28 ⇒ 40d,
- 0x12 ... 0x15 (4 Byte) Bildbreite in Pixel: 0x FA ⇒ 250d,
- 0x16 ... 0x19 (4 Byte) Bildhöhe in Pixel: 0x FA ⇒ 250d,
- 0x1A ... 0x1B (2 Byte) Anzahl der Farbebenen (immer auf 1 gesetzt),
- 0x1C ... 0x1D (2 Byte) Bits per Pixel (BPP): 0x0018 ⇒ 24d,
- 0x1E ... 0x21 (4 Byte) Art der Datenkomprimierung,
- 0x22 ... 0x25 (4 Byte) Größe der Bitmap in Byte: 0x 02 DE 62 ⇒ 188002d,
- 0x26 ... 0x29 (4 Byte) Horizontalauflösung in Pixel/Meter: 0x 26 70 ⇒ 9840d,
- 0x2A ... 0x2D (4 Byte) Vertikalauflösung in Pixel/Meter: 0x 26 70 ⇒ 9840d,
- 0x2E ... 0x31 (4 Byte) Anzahl der verwendeten Farben,
- 0x32 ... 0x35 (4 Byte) Anzahl der wichtigen Farben.
Anschließend beginnt mit „0x 43 2A 23” der Bilddatenbereich (im Beispiel jeweils drei Byte pro Pixel für R – G – B). Da auch hier (beim Intel–Prozessor) die Little–Endian–Byteanordnung gilt, bezeichnen diese Einträge die Farbwerte R = 23, G = 2A, B = 43 (jeweils hexadezimal) bzw. R = 35, G = 42, B = 67 (dezimal) .
Die Bilder auf der nächsten Seite machen deutlich, dass bereits wenige Fehler in Dateikopf (14 Byte) oder Informationsblock (40 Byte) genügen, um ein Bild völlig unbrauchbar zu machen. Der Header einer Multimedia–Datei sollte deshalb besonders geschützt werden. Bei BMP umfasst dieser Header indgesamt 54 Byte.
Übertragungsfehler im Dateikopf und Informationsblock
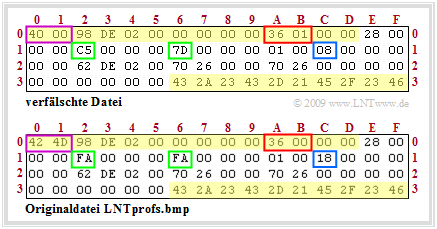
Mit einer Bilderserie sollen die Auswirkungen von Übertragungsfehlern innerhalb von Dateikopf (0x00 ... 0x0D) und Informationsblock (0x0E ... 0x35) verdeutlicht werden. Die linke Abbildung zeigt den Hexadezimal–Dump der verfälschten Datei im Vergleich zur Originaldatei (rechts).
Nachfolgend sehen Sie die Bilder, die sich ergeben, wenn die fünf Fehlerblöcke sukzessive korrigiert werden:
- Die gegebene Datei lässt sich gar nicht öffnen. Korrigiert man die beiden ersten Byte (violette Markierung) von „0x 40 00” in „0x 42 4D”, so ergibt sich das linke obere, einheitlich graue Bild.
- Korrigiert man die Bildbreite von „0x C5” in „0x FA” ⇒ 250d und die Bildhöhe von von „0x 7D” in „0x FA” ⇒ 250d (grüne Markierung), so ergibt sich das mittlere obere Bild bereits mit der richtigen Größe (250 x 250 Pixel), aber immer noch mit grauem Inhalt.
- Zum rechten oberen Bild kommt man durch Berichtigung der Farbtiefe (Bits per Pixel, BPP) von „0x 08” ⇒ 8d auf „0x 18” ⇒ 24d (blaue Markierung), so erkennt man teilweise schon Inhalte.
- Durch Korrektur des roten Fehlerblocks im Bereich 0x0A ... 0x0D (Offset) von „0x 36 01” 54d in „0x 36 00” 54d erhält man schließlich das Originalbild „LNTprofs.bmp”.
BMP–Dateien nach BSC–Verfälschung
Die folgende Bilderserie zeigt den Einfluss von statistisch unabhängigen Fehlern (BSC–Modell) mit folgenden (Bit–)Fehlerwahrscheinlichkeiten:
- $$p = 10^{-3}, \ p = 10^{-2}, \ p = 10^{-1}$.
Der Dateiheader ist jeweils fehlerfrei.
- Bei der oberen Reihe wurde vom Farbbild „LNTprofs.bmp” mit $\rm 24$ Bits per Pixel ausgegangen; der eigentliche Bildbereich umfasst $250 \cdot 250 \cdot 24 = 1.5 \cdot 10^6$ Bit.
- Die untere Reihe basiert auf einem Graustufenbild mit $\rm 8$ Bits per Pixel. Die Datei ist somit etwa um den Faktor $3$ kleiner als die Farbdatei.
Man erkennt aus diesen Darstellungen:
- Die Fehlerwahrscheinlichkeit $p = 10^{-3}$ ist noch nicht allzu störend. Beim Farbbild sind damit etwa $1500$ Bit und auch vergleichsweise ebensoviele Pixel verfälscht (statistische Aussagen). Beim Graustufenbild sind es wegen der kleineren Datei nur etwa $500$ Bitfehler.
- Subjektiv ist der störende Eindruck von Bitfehlern beim Graustufenbild trotz kleinerer Bitfehlerzahl etwa genau so wie beim Farbbild, da sich bei letzterem manche Bitfehler nur in einer marginalen Farbveränderung auswirken.
BMP–Dateien mit Bündelfehlern
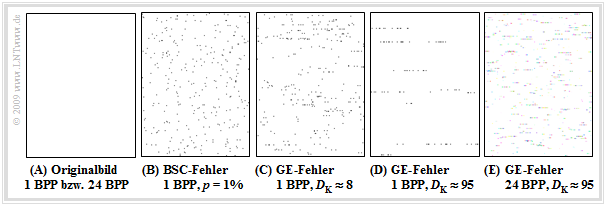
Betrachten wir nun anhand der folgenden Grafik den Einfluss von Bündelfehlern auf BMP–Dateien. Das linke Bild (A) zeigt die Originaldatei „Weiß.bmp” mit ausschließlich weißen Pixeln. Das Ergebnis ist somit unabhängig von der Farbtiefe, doch ist die Datei „Weiß1.bmp” (1 BPP, 4046 Byte) nahezu um den Faktor $24$ kleiner als die Datei „Weiß24.bmp” 24 BPP, 90456 Byte). Nahezu deshalb, weil der Header bei beiden Dateien gleich groß ist und in der 1 BPP–Datei ebenfalls eine Farbtabelle mit enthalten ist.
Bei den vier rechten Bildern sind jeweils Übertragungsfehler mit der (mittleren) Fehlerwahrscheinlichkeit $p_{\rm M} = 1\%$ berücksichtigt. Man erkennt:
- Die Fehler im Bild (B) sind statistisch unabhängig und wurden gemäß dem BSC–Modell generiert. Sie sind zufällig über die gesamte Bildfläche verteilt.
- Dagegen zeigen die Bilder (C) und (D) Bündelfehlerstrukturen nach dem GE–Modell mit unterschiedlichen Fehlerkorrelationsdauern $D_{\rm K} \approx 8$ bzw. $D_{\rm K} \approx 95$. Man erkennt aus der Fehlerstruktur, dass BMP–Bilder zeilenweise abgespeichert werden.
- Bei den Schwarz–Weiß–Bildern (1 BPP) (B), (C) und (D) ist im statistischen Mittel jedes 100. Pixel verfälscht. Beim Bild (E) mit 24 BPP (True Color) gibt es demgegenüber trotz gleicher mittlerer Fehlerwahrscheinlichkeit $p_{\rm M} = 1\%$ mehr Pixelverfälschungen.
- Ein Vergleich der Bilder (D) und (E) zeigt die unterschiedlichen Korrelationsdauern bezogen auf Pixel ($D_{\rm K} \approx 95$ gegenüber $D_{\rm K} \approx 95/24 \approx 4$). Außerdem erkennt man, dass im Bild (E) die Fehlerpixel farbig sind.
Auswirkungen von Übertragungsfehlern auf Audios
Das WAVE-Dateiformat ist ein Containerformat zur digitalen Speicherung von Audiodaten, das auf dem von Microsoft für Windows definierten Resource Interchange File Format (RIFF) aufsetzt. Der besonders zu schützende Dateiheader umfasst bei WAVE–Dateien 43 Byte.
Enthalten sind meist sogenannte PCM-Rohdaten, also eine zeit- und wertdiskrete Darstellung des zeitlichen Verlaufs eines Signals. Die Qualität des aufgezeichneten Klangs hängt dann von zwei Werten ab, nämlich
- der Abtastrate (Anzahl der Abtastwerte pro Zeiteinheit),
- der Auflösung (Bit-Tiefe).
Wir demonstrieren zunächst den Einfluss von Übertragungsfehlern auf die Audiodatei „Stille.wav” mit ca. 10 Sekunden Dauer. Das heißt: Alles, was Sie hören, sind Übertragungsfehler.
Statistisch unabhängige Fehler entsprechend dem BSC–Modell
Bei den folgenden WAVE-Dateien beginnen wir mit dem BSC–Parameter $p= 10^{-5}$ und erhöhen diesen bis zu $p= 10\%$. $p$ gibt gleichzeitig die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$ an, die auch als Bit Error Rate (BER) bezeichnet wird. Jeweils angegeben ist auch die subjektive Einschätzung des Autors.
$p=10^{-5}$ ⇒ Kaum hörbar.
$p=10^{-4}$ ⇒ Noch nicht sehr störend.
$p=10^{-3}$ ⇒ Merkbar störend.
$p=10^{-2}$ ⇒ Warnung vor dem Öffnen.
$p=10^{-1}$ ⇒ Nur für extrem Lärmunempfindliche geeignet.
Gegenüberstellung von statistisch unabhängigen Fehlern und Bündelfehlern
- Die statistisch unabhängigen Fehler wurden wieder mit dem BSC–Modell generiert. Die mittlere Fehlerwahrscheinlichkeit beträgt $p_{\rm M}=10^{-3}$.
- Für die Generierung der Bündelfehler wurde das Kanalmodell nach Gilbertndash;Elliott (GE) verwendet.
- Die mittlere Fehlerwahrscheinlichkeit beträgt auch hier $p_{\rm M}=10^{-3}$.
- Gegenübergestellt wird die sehr kurze Korrelationsdauer $D_{\rm K}= 8$ mit weitweichenden statistischen Bindungen ⇒ $D_{\rm K}= 1000$.
Zunächst gehen wir wieder von der Datei „Stille.wav” aus. Man erkennt, dass eine kurze Fehlerkorrelationsdauer des GE–Modells im Ergebnis sich nicht allzu sehr von statistisch unabhängigen Fehlern unterscheidet, da jeder Abtastwert mit 16 Bit dargestellt wird. Was ist mit $D_{\rm K}= 1000$?
BSC–Modell.
GE–Modell mit $D_{\rm K}= 8$.
GE–Modell mit $D_{\rm K}= 1000$.
Auch beim nachfolgenden kurzen Musikstück gelten die gleichen Kanalparameter und man erkennt ähnliche Eigenschaften.
BSC–Modell.
GE–Modell mit $D_{\rm K}= 8$.
GE–Modell mit $D_{\rm K}= 1000$.
Hinweis: Alle BMP–Bilder und WAV–Audios zu diesem Kapitel wurden mit dem Windows–Programm „Digitale Kanalmodelle & Multimedia” aus dem (früheren) Praktikum „Simulation Digitaler Übertragungssysteme ” am Lehrstuhl für Nachrichtentechnik der TU München erzeugt. Die folgenden Links stellen bereit:
- das Windows-Programm DKM ⇒ Link verweist auf die ZIP-Version des Programms; und
- die zugehörige Praktikumsanleitung ⇒ Link verweist auf die PDF-Version.
Aufgaben zum Kapitel
Zusatzaufgaben:5.8 Verfälschung von BMP-Bildern