Aufgaben:Exercise 2.2: Simple Two-Path Channel Model: Unterschied zwischen den Versionen
Javier (Diskussion | Beiträge) |
Javier (Diskussion | Beiträge) |
||
| (15 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Mehrwegeempfang beim Mobilfunk}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Mehrwegeempfang beim Mobilfunk}} | ||
| − | [[Datei: | + | [[Datei:EN_Mob_A_2_2.png|right|frame|Two equivalent models <br>for the two-path channel]] |
| − | Here we consider a two- | + | Here we consider a two-path channel for mobile radio according to the adjacent graph, characterized by the model parameters |
| − | :$$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \ | + | :$$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$ |
Two different numerical values are considered for the damping factor on the secondary path: | Two different numerical values are considered for the damping factor on the secondary path: | ||
* $k_2 = 2 \cdot 10^{-5}$ ⇒ subtasks '''(1)''' to '''(4)''', | * $k_2 = 2 \cdot 10^{-5}$ ⇒ subtasks '''(1)''' to '''(4)''', | ||
| − | * $k_2 = 10^{-4}$ ⇒ subtasks '''(5)'' and '''(6)'''. | + | * $k_2 = 10^{-4}$ ⇒ subtasks '''(5)''' and '''(6)'''. |
| Zeile 16: | Zeile 16: | ||
| − | An important descriptive parameter of any mobile radio system is the coherence bandwidth $B_{\rm K}$, which is defined in the chapter [[ | + | An important descriptive parameter of any mobile radio system is the coherence bandwidth $B_{\rm K}$, which is defined in the chapter [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| GWSSUS–Kanalmodell]] . The coherence bandwidth indicates whether the system can be approximated as non-frequency-selective: |
*This is justified if the signal bandwidth $B_{\rm S}$ is significantly smaller than the coherence bandwidth $B_{\rm K}$. | *This is justified if the signal bandwidth $B_{\rm S}$ is significantly smaller than the coherence bandwidth $B_{\rm K}$. | ||
| − | *Otherwise, the mobile radio system is frequency selective, which requires a more complicated description. | + | *Otherwise, the mobile radio system is frequency-selective, which requires a more complicated description. |
As a simple approximation for the coherence bandwidth, the reciprocal value of pulse broadening is often used in the literature (marked by an apostrophe in our learning tutorial): | As a simple approximation for the coherence bandwidth, the reciprocal value of pulse broadening is often used in the literature (marked by an apostrophe in our learning tutorial): | ||
| − | :$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\ | + | :$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$ |
| Zeile 33: | Zeile 33: | ||
* This task belongs to the topic of the chapter [[Mobile_Kommunikation/Mehrwegeempfang_beim_Mobilfunk| Mehrwegeempfang beim Mobilfunk]]. | * This task belongs to the topic of the chapter [[Mobile_Kommunikation/Mehrwegeempfang_beim_Mobilfunk| Mehrwegeempfang beim Mobilfunk]]. | ||
* For the solution you also need the speed of light $c = 3 \cdot 10^8 \ \rm m/s$. | * For the solution you also need the speed of light $c = 3 \cdot 10^8 \ \rm m/s$. | ||
| − | * For $k_2$ only positive values are used here | + | * For $k_2$ only positive values are used here. However, as you may remember,if the secondary path is created by reflection on a wall, a phase change by $\pi$ occurs, resulting in a negative value of $k_2$. |
| Zeile 49: | Zeile 49: | ||
$\tau_0 \ = \ ${ 1 3% } $\ \ \rm µ s$ | $\tau_0 \ = \ ${ 1 3% } $\ \ \rm µ s$ | ||
| − | {Calculate the magnitude frequency response ⇒ $|H_0(f)|$ of the simplified model for the frequencies $f = 0$, $f = 250 \ \rm kHz$ and $f = 500 \ \rm kHz$ | + | {Calculate the magnitude of the frequency response ⇒ $|H_0(f)|$ of the simplified model for the frequencies $f = 0$, $f = 250 \ \rm kHz$ and $f = 500 \ \rm kHz$ |
|type="{}"} | |type="{}"} | ||
$|H_0(f = 0)| \ = \ ${ 1.2 3% } | $|H_0(f = 0)| \ = \ ${ 1.2 3% } | ||
| Zeile 55: | Zeile 55: | ||
$|H_0(f = 500 \ \rm kHz)| \ = \ ${ 0.8 3% } | $|H_0(f = 500 \ \rm kHz)| \ = \ ${ 0.8 3% } | ||
| − | { | + | {For which signal frequencies $f_{\rm S}$ does destructive interference occur here? |
|type="[]"} | |type="[]"} | ||
+ $f_{\rm S} = 500 \ \rm kHz$, | + $f_{\rm S} = 500 \ \rm kHz$, | ||
| Zeile 61: | Zeile 61: | ||
- $f_{\rm S} = 1 \ \rm MHz$. | - $f_{\rm S} = 1 \ \rm MHz$. | ||
| − | { | + | {What is the approximate coherence bandwidth for $k_2 = 2 \cdot 10^{-5}$ or. $k_2 = 10^{-4}$ ? |
|type="{}"} | |type="{}"} | ||
| − | $k_2 = 2 \cdot 10^{-5} \text \ \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ ${ 1 3% } $\ \rm MHz | + | $k_2 = 2 \cdot 10^{-5} \text{:} \ \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ ${ 1 3% } $\ \rm MHz |
| − | $k_2 = 10^{-4} \text \ \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ ${ 1 3% } $\ \rm MHz | + | $k_2 = 10^{-4} \text{:} \ \hspace{0.4cm} B_{\rm K}\hspace{0.01cm}' = \ ${ 1 3% } $\ \rm MHz |
| − | {Which statements are correct regarding frequency selectivity | + | {Which statements are correct regarding frequency selectivity if $B_{\rm S}$ denotes the signal bandwidth? |
|type="[]"} | |type="[]"} | ||
- For GSM: $(B_{\rm S} = 200 \ \rm kHz)$ the channel is frequency selective. | - For GSM: $(B_{\rm S} = 200 \ \rm kHz)$ the channel is frequency selective. | ||
| Zeile 74: | Zeile 74: | ||
===Sample solution=== | ===Sample solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' We have $\tau_1 = d_1/c$ ⇒ $ d_1 = \tau_1 \cdot c = 10^{-5} \rm s \cdot 3 \cdot 10^8 \ m/s \ \ \underline {= 3 \ km}$. |
| Zeile 81: | Zeile 81: | ||
'''(3)''' The impulse location is | '''(3)''' The impulse location is | ||
| − | $$h_{\rm 0}(\ | + | $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$ |
By Fourier transformation you get the frequency response | By Fourier transformation you get the frequency response | ||
| − | :$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \ | + | :$$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin |
}( 2 \pi f \tau_0) | }( 2 \pi f \tau_0) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | and thus to the following magnitude frequency response: | + | and thus to the following magnitude of the frequency response: |
$$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} | $$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ | \Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ | ||
| Zeile 94: | Zeile 94: | ||
$$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$ | $$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$ | ||
| − | [[File:P_ID2158__Mob_A_2_2c.png|right|frame| | + | [[File:P_ID2158__Mob_A_2_2c.png|right|frame|Magnitude of the frequency response of a two-way channel]] |
The graphic (red curve) shows the function $|H_0(f)|$. | The graphic (red curve) shows the function $|H_0(f)|$. | ||
*The values you are looking for are marked by the yellow dots. | *The values you are looking for are marked by the yellow dots. | ||
| Zeile 101: | Zeile 101: | ||
| − | '''(4)''' | + | '''(4)''' <u>Solution 1</u> is correct: |
| − | *Destructive | + | *Destructive interference occurs for $|H_0(f)| < 1$, for example for $f = 500 \ \rm kHz$. |
*On the other hand: | *On the other hand: | ||
:$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$ | :$$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$ | ||
| − | :$$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$ | + | :$$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$$ |
| − | '''(5)''' The difference $\tau_{\rm max} \ – \tau_{\rm min}$ | + | '''(5)''' The difference $\tau_{\rm max} \ – \tau_{\rm min}$ between the delays in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$. |
| − | *So the coherence bandwidth | + | *So the coherence bandwidth is |
| − | :$$B_{\rm K}\hspace{0.01cm}' = {1}/{\ | + | :$$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$ |
*The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way. | *The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way. | ||
| − | * | + | *This approximation $B_{\rm K}\hspace{0.01cm}'$ of the coherence bandwidth is shown in the graph. |
| − | '''(6)''' | + | '''(6)''' <u>Solution 2</u> is correct: |
| − | *The channel is | + | *The channel is non-frequency-selective if the coherence bandwidth $B_{\rm K}$ is significantly larger than the signal bandwidth $B_{\rm S}$. |
| − | *For the given channel, this is true for GSM, but not for UMTS. For UMTS | + | *For the given channel, this is true for GSM, but not for UMTS. For UMTS, this is frequency-selective channel. |
| − | + | {{ML-Fuß}} | |
[[Category:Exercises for Mobile Communications|^2.2 Multi-Path Reception in Wireless Systems^]] | [[Category:Exercises for Mobile Communications|^2.2 Multi-Path Reception in Wireless Systems^]] | ||
Aktuelle Version vom 20. Mai 2020, 17:41 Uhr
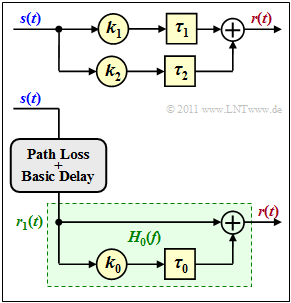
Here we consider a two-path channel for mobile radio according to the adjacent graph, characterized by the model parameters
- $$k_1 = 10^{-4}\hspace{0.05cm}, \hspace{0.2cm} \tau_{1} = 10\,{\rm µ s}\hspace{0.05cm}, \hspace{0.2cm}\tau_{2} = 11\,{\rm µ s} \hspace{0.05cm}.$$
Two different numerical values are considered for the damping factor on the secondary path:
- $k_2 = 2 \cdot 10^{-5}$ ⇒ subtasks (1) to (4),
- $k_2 = 10^{-4}$ ⇒ subtasks (5) and (6).
An equivalent channel model is shown below, with only the part highlighted in green being considered further. This means:
- The basic attenuation (path loss) and the basic propagation time are not taken into account here.
- The frequency response of this $(k_0, \tau_0$)–model is designated $H_0(f)$ .
An important descriptive parameter of any mobile radio system is the coherence bandwidth $B_{\rm K}$, which is defined in the chapter GWSSUS–Kanalmodell . The coherence bandwidth indicates whether the system can be approximated as non-frequency-selective:
- This is justified if the signal bandwidth $B_{\rm S}$ is significantly smaller than the coherence bandwidth $B_{\rm K}$.
- Otherwise, the mobile radio system is frequency-selective, which requires a more complicated description.
As a simple approximation for the coherence bandwidth, the reciprocal value of pulse broadening is often used in the literature (marked by an apostrophe in our learning tutorial):
- $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$
Notes:
- This task belongs to the topic of the chapter Mehrwegeempfang beim Mobilfunk.
- For the solution you also need the speed of light $c = 3 \cdot 10^8 \ \rm m/s$.
- For $k_2$ only positive values are used here. However, as you may remember,if the secondary path is created by reflection on a wall, a phase change by $\pi$ occurs, resulting in a negative value of $k_2$.
Questionnaire
Sample solution
(2) The damping factor is $k_0 = k_2/k_1 \ \ \underline {= 0.2}$ and the delay time $\tau_0 = \tau_2 \ – \tau_1 \ \underline {= 1 \ \ \rm µ s}$.
- The path loss effective for both paths is thus $k_1 = 10^{-4}$ and the basic delay time is $\tau_1 = 10 \ \ \rm µ s$.
(3) The impulse location is $$h_{\rm 0}(\tau) = \delta(\tau) + k_0 \cdot \delta(\tau - \tau_0) \hspace{0.05cm}.$$
By Fourier transformation you get the frequency response
- $$H_{\rm 0}(f) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 + k_0 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_0}=1 + k_0 \cdot {\cos}( 2 \pi f \tau_0) + {\rm j}\cdot k_0 \cdot {\sin }( 2 \pi f \tau_0) \hspace{0.05cm},$$
and thus to the following magnitude of the frequency response: $$|H_{\rm 0}(f)| = \sqrt{ \left [ 1 + k_0 \cdot {\cos}( 2 \pi f \tau_0)\right ]^2 + k_0^2 \cdot {\sin^2 }( 2 \pi f \tau_0)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|H_{\rm 0}(f = 0)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1+ k_0 \hspace{0.1cm} \underline {=1.2} \hspace{0.05cm},$$ $$|H_{\rm 0}(f = 250\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi/2)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi/2)} = \sqrt{1+ k_0^2} \hspace{0.1cm} \underline {\approx 1.02} \hspace{0.05cm},$$ $$|H_{\rm 0}(f = 500\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{ \left [ 1 + k_0 \cdot {\cos}( \pi)\right ]^2 + k_0^2 \cdot {\sin^2 }( \pi)} = {1- k_0} \hspace{0.1cm} \underline {= 0.8} \hspace{0.05cm}.$$
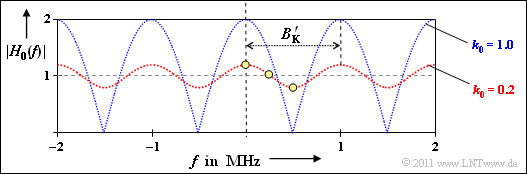
The graphic (red curve) shows the function $|H_0(f)|$.
- The values you are looking for are marked by the yellow dots.
- The blue curve refers to the subtask (5) with $k_0 = 1 \ \Rightarrow \ k_2 = k_0 \cdot k_1 = 10^{–4}$.
(4) Solution 1 is correct:
- Destructive interference occurs for $|H_0(f)| < 1$, for example for $f = 500 \ \rm kHz$.
- On the other hand:
- $$|H_{\rm 0}(f = 750\,{\rm kHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 250\,{\rm kHz})| \approx 1.02 > 1\hspace{0.05cm},$$
- $$|H_{\rm 0}(f = 1\,{\rm MHz})| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} |H_{\rm 0}(f = 0)| = 1.2 > 1 \hspace{0.05cm}.$$
(5) The difference $\tau_{\rm max} \ – \tau_{\rm min}$ between the delays in the two paths is equal to $\tau_0 = 1 \ \ \rm µ s$.
- So the coherence bandwidth is
- $$B_{\rm K}\hspace{0.01cm}' = {1}/{\tau_{\rm 0} } \hspace{0.1cm} \underline {=1\,{\rm MHz}} \hspace{0.05cm}.$$
- The result is independent from $k_2$. It applies to $k_2 = 2 \cdot 10^{-5} \Rightarrow k_0 = 0.2$ and $k_2 = 10^{-4} \Rightarrow k_0 = $1 in the same way.
- This approximation $B_{\rm K}\hspace{0.01cm}'$ of the coherence bandwidth is shown in the graph.
(6) Solution 2 is correct:
- The channel is non-frequency-selective if the coherence bandwidth $B_{\rm K}$ is significantly larger than the signal bandwidth $B_{\rm S}$.
- For the given channel, this is true for GSM, but not for UMTS. For UMTS, this is frequency-selective channel.