Aufgaben:Aufgabe 5.8Z: Matched-Filter bei Rechteck-Störleistungsspektrum: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
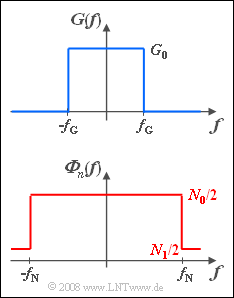
| − | [[Datei:P_ID647__Sto_Z_5_8.png|right|frame|Spektrum $G(f)$ | + | [[Datei:P_ID647__Sto_Z_5_8.png|right|frame|Nutzsignal–Spektrum $G(f)$ und LDS ${\it \Phi}_n (f)$ der Störung]] |
Die bei einem System wirksame Störleistungsdichte kann als bereichsweise konstant angenommen werden: | Die bei einem System wirksame Störleistungsdichte kann als bereichsweise konstant angenommen werden: | ||
:$$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{f\ddot{u}r} \\ \rm{f\ddot{u}r} \\\end{array}\quad \begin{array}{*{20}c} {\left| f \right| \le f_{\rm N} ,} \\ {\left| f \right| > f_{\rm N} .} \\\end{array}$$ | :$$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{f\ddot{u}r} \\ \rm{f\ddot{u}r} \\\end{array}\quad \begin{array}{*{20}c} {\left| f \right| \le f_{\rm N} ,} \\ {\left| f \right| > f_{\rm N} .} \\\end{array}$$ | ||
| − | *Hierbei sei die Störleistungsdichte $N_1$ im äußeren Bereich $|f| > f_{\rm N}$ stets sehr viel kleiner als $N_0$. | + | *Hierbei sei die Störleistungsdichte $N_1$ im äußeren Bereich $|f| > f_{\rm N}$ stets sehr viel kleiner als $N_0$. |
*Verwenden Sie zum Beispiel die folgenden Werte: | *Verwenden Sie zum Beispiel die folgenden Werte: | ||
:$$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$ | :$$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$ | ||
| − | Ein solches Störsignal $n(t)$ tritt | + | Ein solches Störsignal $n(t)$ tritt zum Beispiel auf, wenn die dominante Störquelle nur Anteile unterhalb der Grenzfrequenz $f_{\rm N}$ beinhaltet. Aufgrund des unvermeidbaren thermischen Rauschens ist auch für $|f| > f_{\rm N}$ die Störleistungsdichte ${\it \Phi}_n(f) \ne 0$. |
Weiter gelte: | Weiter gelte: | ||
| − | *Das Spektrum $G(f)$ des Nutzsignals sei entsprechend der obigen Skizze ebenfalls rechteckförmig. | + | *Das Spektrum $G(f)$ des Nutzsignals sei entsprechend der obigen Skizze ebenfalls rechteckförmig. |
| − | *Der zugehörige Nutzimpuls $g(t)$ hat deshalb mit $\Delta f = 2 \cdot f_{\rm G}$ den folgenden Verlauf: | + | *Der zugehörige Nutzimpuls $g(t)$ hat deshalb mit $\Delta f = 2 \cdot f_{\rm G}$ den folgenden Verlauf: |
:$$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} \left( {{\rm{\pi }} \cdot \Delta f \cdot t} \right).$$ | :$$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} \left( {{\rm{\pi }} \cdot \Delta f \cdot t} \right).$$ | ||
| − | *Das Empfangsfilter sei optimal an das Nutzspektrum $G(f)$ und das Störleistungsdichtespektrums ${\it \Phi}_n(f)$ angepasst. | + | *Das Empfangsfilter sei optimal an das Nutzspektrum $G(f)$ und das Störleistungsdichtespektrums ${\it \Phi}_n(f)$ angepasst. |
| − | *Das heißt, es gelte $H_{\rm E}(f) = H_{\rm MF}(f)$. Der Detektionszeitpunkt sei vereinfachend $T_{\rm D} = 0$ (akausale Systembeschreibung). | + | *Das heißt, es gelte $H_{\rm E}(f) = H_{\rm MF}(f)$. Der Detektionszeitpunkt sei vereinfachend $T_{\rm D} = 0$ (akausale Systembeschreibung). |
| + | |||
| + | |||
| Zeile 27: | Zeile 29: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Matched-Filter|Matched-Filter]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Matched-Filter|Matched-Filter]]. |
*Verwenden Sie für numerische Berechnungen stets die Zahlenwerte | *Verwenden Sie für numerische Berechnungen stets die Zahlenwerte | ||
| Zeile 37: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der folgenden Aussagen gelten unter der Voraussetzung $f_{\rm N} > f_{\rm G}$? | + | {Welche der folgenden Aussagen gelten unter der Voraussetzung $f_{\rm N} > f_{\rm G}$? |
|type="[]"} | |type="[]"} | ||
+ Anwendbar ist das „Matched-Filter” für „Weißes Rauschen”. | + Anwendbar ist das „Matched-Filter” für „Weißes Rauschen”. | ||
- Der MF–Ausgangsimpuls ist dreieckförmig. | - Der MF–Ausgangsimpuls ist dreieckförmig. | ||
| − | + Der MF–Ausgangsimpuls ist $\rm si$–förmig. | + | + Der MF–Ausgangsimpuls ist $\rm si$–förmig. |
| − | - Der MF–Ausgangsimpuls ist $\rm si^2$–förmig. | + | - Der MF–Ausgangsimpuls ist $\rm si^2$–förmig. |
| − | {Welches S/N–Verhältnis (in dB) ergibt sich für $f_{\rm N} > f_{\rm G}$? | + | {Welches S/N–Verhältnis (in dB) ergibt sich für $f_{\rm N} > f_{\rm G}$? |
|type="{}"} | |type="{}"} | ||
$10 \cdot \lg \; \rho_d \ = \ $ { 20 3% } $\ \rm dB$ | $10 \cdot \lg \; \rho_d \ = \ $ { 20 3% } $\ \rm dB$ | ||
| − | {Welches SNR (in dB) ergibt sich für $f_{\rm N} = f_{\rm G}/2$? Interpretation. | + | {Welches SNR (in dB) ergibt sich für $f_{\rm N} = f_{\rm G}/2$? Interpretation. |
|type="{}"} | |type="{}"} | ||
$10 \cdot \lg \; \rho_d \ = \ $ { 37.03 3% } $\ \rm dB$ | $10 \cdot \lg \; \rho_d \ = \ $ { 37.03 3% } $\ \rm dB$ | ||
Version vom 10. Dezember 2019, 12:16 Uhr
Die bei einem System wirksame Störleistungsdichte kann als bereichsweise konstant angenommen werden:
- $$\it{\Phi} _n \left( f \right) = \left\{ \begin{array}{l} N_0 /2 \\ N_1 /2 \\ \end{array} \right.\quad \begin{array}{*{20}c} \rm{f\ddot{u}r} \\ \rm{f\ddot{u}r} \\\end{array}\quad \begin{array}{*{20}c} {\left| f \right| \le f_{\rm N} ,} \\ {\left| f \right| > f_{\rm N} .} \\\end{array}$$
- Hierbei sei die Störleistungsdichte $N_1$ im äußeren Bereich $|f| > f_{\rm N}$ stets sehr viel kleiner als $N_0$.
- Verwenden Sie zum Beispiel die folgenden Werte:
- $$N_0 = 2 \cdot 10^{ - 6} \;{\rm{V}}^{\rm{2}} /{\rm{Hz}},\quad N_1 = 2 \cdot 10^{ - 8} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$
Ein solches Störsignal $n(t)$ tritt zum Beispiel auf, wenn die dominante Störquelle nur Anteile unterhalb der Grenzfrequenz $f_{\rm N}$ beinhaltet. Aufgrund des unvermeidbaren thermischen Rauschens ist auch für $|f| > f_{\rm N}$ die Störleistungsdichte ${\it \Phi}_n(f) \ne 0$.
Weiter gelte:
- Das Spektrum $G(f)$ des Nutzsignals sei entsprechend der obigen Skizze ebenfalls rechteckförmig.
- Der zugehörige Nutzimpuls $g(t)$ hat deshalb mit $\Delta f = 2 \cdot f_{\rm G}$ den folgenden Verlauf:
- $$g(t) = G_0 \cdot \Delta f \cdot {\mathop{\rm si}\nolimits} \left( {{\rm{\pi }} \cdot \Delta f \cdot t} \right).$$
- Das Empfangsfilter sei optimal an das Nutzspektrum $G(f)$ und das Störleistungsdichtespektrums ${\it \Phi}_n(f)$ angepasst.
- Das heißt, es gelte $H_{\rm E}(f) = H_{\rm MF}(f)$. Der Detektionszeitpunkt sei vereinfachend $T_{\rm D} = 0$ (akausale Systembeschreibung).
Hinweise:
- Die Aufgabe gehört zum Kapitel Matched-Filter.
- Verwenden Sie für numerische Berechnungen stets die Zahlenwerte
- $$G_0 = 10^{ - 4} \;{\rm{V/Hz}}{\rm{, }}\quad \Delta f = 10\;{\rm{kHz}}.$$
Fragebogen
Musterlösung
(1) Richtig sind die Lösungsvorschläge 1 und 3:
- Für alle Frequenzen $|f| > f_{\rm G}$, bei denen das Nutzsignal Spektralanteile besitzt $(G_d(f) \ne 0)$, ist das Störleistungsdichtespektrum ${\it}\Phi_n(f) = N_0/2$.
- Damit lautet der Frequenzgang des Matched-Filters, $T_{\rm D} = 0$ vorausgesetzt:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G(f).$$
- Der optimale Frequenzgang $H_{\rm MF}(f)$ ist in diesem Fall ebenso wie $G(f)$ rechteckförmig mit Breite $\Delta f$.
- Für den Nutzanteil des MF-Ausgangssignals gilt somit:
- $$d_{\rm S}(t)\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \quad G(f) \cdot H_{\rm MF} (f).$$
- Das Produkt zweier Rechteckfunktionen gleicher Breite ergibt wiederum diese Rechteckfunktion.
- Daraus folgt weiter, dass der Ausgangsimpuls des Matched-Filters ebenfalls $\rm si$-förmig verläuft.
(2) Bei weißem Rauschen erhält man:
- $$\rho _d = \frac{1}{N_0 /2}\int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^2 \, {\rm{d}}f.}$$
- Das Integral liefert den Wert $G_0^2 \cdot \Delta f$.
- Daraus folgt:
- $$\rho _d = \frac{G_0 ^2 \cdot \Delta f }{N_0 /2} = \frac{ 10^{ - 8}\,(\rm V/Hz)^2 \;\cdot10^4 \;{\rm{Hz}} }{10^{ - 6}\,\rm V^2/Hz} = 10^2 \quad \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline { = 20\;{\rm{dB}}}.$$
(3) Allgemein gilt für das SNR bei farbiger Störung:
- $$\rho _d = 2 \cdot \int_0^\infty \frac{\left| {G(f)} \right|^2 }{{\it \Phi}_n (f)} \, {\rm{d}}f.$$
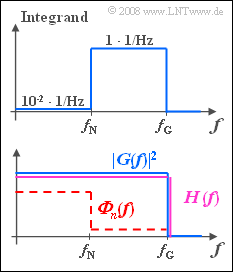
- Wie aus der nebenstehenden qualitativen Skizze hervorgeht, ist der Integrand bei den vorgegebenen Frequenzgängen stückweise konstant.
- Mit $f_{\rm G} = 5 \; \rm kHz$ und $f_{\rm N} = f_{\rm G}/2 = 2.5 \; \rm kHz$ erhält man somit:
- $$\rho _d = 2 \cdot 2.5\;{\rm{kHz}}\left( { \frac{10^{ - 2}}{\rm{Hz}} + \frac{1}{{{\rm{Hz}}}} } \right) = 5.05 \cdot 10^3 \quad \Rightarrow \quad 10\cdot\lg \rho _d \hspace{0.15cm}\underline {= 37.03\;{\rm{dB}}}.$$
Interpretation:
- Der Matched–Filter–Frequenzgang $H_{\rm MF}(f)$ hat genau den selben Verlauf wie der oben skizzierte Integrand.
- Wird die Konstante $K_{\rm MF}$ (willkürlich) so gewählt, dass im Bereich $f_{\rm N} \le |f| \le f_{\rm G}$ der MF–Frequenzgang den Wert $1$ besitzt, so gilt für tiefe Frequenzen $(|f| < f_{\rm G})$: $H_{\rm MF}(f) = 0.01$. Das bedeutet:
- Das Matched–Filter bevorzugt diejenigen Frequenzen, die durch die Störung ${\it \Phi}_n(f)$ nur wenig beeinträchtigt werden.
- Würde man stattdessen ein Filter $H(f)$ verwenden, das alle Frequenzen des Nutzsignals bis einschließlich $f_{\rm G}$ gleich bewertet (violetter Kurvenverlauf in der unteren Skizze), so ergäben sich folgende Verhältnisse:
- $$d_{\rm S}( {T_{\rm D} } ) = G_0 \cdot 2 \cdot f_{\rm G} = 1\;{\rm{V}}, \quad \sigma _d ^2 = 10^{ - 6} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot f_{\rm G} + 10^{ - 8} \frac{{{\rm{V}}^{\rm{2}} }}{{{\rm{Hz}}}} \cdot ( {f_{\rm G} - f_{\rm N} } ) = 2.5 \cdot 1.01 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}$$
- $$ \Rightarrow \hspace{0.3cm} \rho _d = \frac {d_{\rm S}( {T_{\rm D} } )^2}{\sigma _d ^2} = \frac{1 \;{\rm{V}}^{\rm{2}}}{2.525 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}}} = 396 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \, \rho _d = 25.98 \, {\rm dB}.$$
- Das Signal–zu–Rauschverhältnis ist somit um ca. $11\ \rm dB$ schlechter, als wenn man das Matched–Filter für farbige Störungen verwendet.