Aufgaben:Aufgabe 5.8: Matched-Filter für farbige Störung

• Zurück zum Buch

Am Eingang eines Filters liegt ein Gaußimpuls

$$g(t) = g_0 \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t} \right)^2 }$$

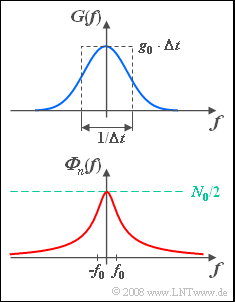
mit Amplitude $g_0 = 2 \hspace{0.05cm}\rm V$ und äquivalenter Impulsdauer $\Delta t = 1 \hspace{0.05cm}\rm ms$ an. Die dazugehörige Spektralfunktion $G(f)$ ist oben skizziert. Die Energie dieses Gaußimpulses ist wie folgt gegeben:

$$E_g = \int_{ - \infty }^{ + \infty } {g\left( t \right)^2 {\rm{d}}t = \frac{g_0 ^2 \cdot \Delta t}{\sqrt 2 }} = 2.83 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}} {\rm{s}}.$$

Dem Impuls $g(t)$ ist eine Störung $n(t)$ überlagert, die den Impuls weitgehend überdeckt. Hierfür werden zwei Alternativen betrachtet:

• Die zweiseitige Störleistungsdichte sei konstant (nur bei der ersten Teilaufgabe):

$${\it \Phi}_n (f) = \frac{N_0 }{2},\quad N_0 = 10^{ - 6} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}.$$

• Das Störsignal n(t) sei farbig mit folgender Störleistungsdichte:

$${\it \Phi}_n (f) = \frac{N_0 /2}{{1 + \left( {f/f_0 } \right)^2 }},\quad f_0 = 500\;{\rm{Hz}}.$$

Dieser zweite LDS-Verlauf kann zum Beispiel aus weißem Rauschen durch ein Formfilter mit dem Frequenzgang

$$H_{\rm N}(f) = \frac{1}{{1 + {\rm{j}}f/f_0 }}\quad\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \quad h_{\rm N}(t) = 2{\rm{\pi }}f_0 \cdot {\rm{e}}^{ - 2{\rm{\pi }}f_0 t} $$

modelliert werden (Tiefpass erster Ordnung). Weiter soll gelten:

• Das Filter sei jeweils optimal an die Sendeimpulsform $g(t)$ und das Störleistungsdichtespektrum ${\it \Phi}_n (f)$ angepasst:   $H(f) = H_{\rm MF}(f)$.
• Die Filterkonstante $K_{\rm MF}$ ist so zu wählen, dass $H(f= 0) =1$ wird.
• Der Detektionszeitpunkt sei vereinfachend $T_{\rm D}= 0$ (akausale Systembeschreibung).

Hinweise:

• Die Aufgabe gehört zum Kapitel Matched-Filter.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gegeben ist zudem das folgende bestimmte Integral:

$$\frac{1}{{\sqrt {2{\rm{\pi }}} }}\int_{ - \infty }^{ + \infty } {x^2 \cdot {\rm e}^{ - x^2 /2} \,\,{\rm{d}}x} = 1.$$

Fragebogen

1

Wie groß ist das S/N–Verhältnis (in dB) im Fall des weißen Rauschens?

$10 \cdot \lg \hspace{0.1cm} \rho_{d,\hspace{0.08cm} \rm WR} \ = $ $\ \rm dB$

2

Berechnen Sie den MF–Frequenzgang bei den vorliegenden farbigen Störungen. Welchen Wert besitzt H_MF(f) bei f = 1 kHz betragsmäßig?

$|H_\text{MF}(f = 1 \hspace{0.05cm} \rm kHz)| \ = $

3

Welches S/N–Verhältnis stellt sich im Fall der vorgegebenen farbigen Störung am Empfänger ein? Begründen Sie das bessere Ergebnis.

$10 \cdot \lg \hspace{0.1cm} \rho_d \ = $ $\ \rm dB$

Musterlösung

Musterlösung

(1)  Bei weißem Rauschen gilt nach den allgemeinen Gleichungen im Theorieteil:

$$\rho_{d, \rm WR} = \frac{2E_g }{N_0 } = \frac{{2 \cdot 2.83 \cdot 10^{ - 3} \;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{10^{ - 6} \;{\rm{V}}^{\rm{2}}/ {\rm{Hz}}}} = 5.66 \cdot 10^3 \quad \Rightarrow \quad 10\lg \cdot \rho _{d, \rm WR} \hspace{0.15cm}\underline {= 37.53\;{\rm{dB}}}.$$

(2)  Für den Frequenzgang bei farbigen Störungen gilt unter der Bedingung $T_{\rm D}= 0$:

$$H_\text{MF} (f) = K_\text{MF}\cdot \frac{G^{\star} (f)}{\left| {H_{\rm N} (f)} \right|^2 }\hspace{0.2cm}{\rm mit}\hspace{0.15cm} G(f) = g_0 \cdot \Delta t \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t \hspace{0.03cm}\cdot \hspace{0.03cm}f} \right)^2 } ,\hspace{0.15cm}\frac{1}{\left| {H_{\rm N} (f)} \right|^2 } =1+\left( f/f_0 \right)^2. $$

Aus der Bedingung $H_\text{MF}(f = 0) = 1$ folgt $K_\text{MF} = 1/(g_0 \cdot \Delta t)$. Damit erhält man:

$$H_{\rm MF} (f) = {\rm{e}}^{ - {\rm{\pi }}[ {\Delta t \cdot f} ]^2 } \cdot \left( {1 + \left(f/f_0 \right)^2 } \right).$$

Bei weißem (frequenzunabhängigen) Rauschen wäre das Matched-Filter allein durch den ersten Term gegeben, der die Anpassung an den Nutzimpuls $g(t)$ bewirkt. Bei farbigen Störungen  ⇒  Störleistungsdichtespektrum ${\it \Phi}_n(f)$ werden höhere Frequenzen durch den Korrekturterm $1+\left( f/f_0 \right)^2$ angehoben, da in diesem Bereich die Störungen geringer sind. Für $f = 1/\Delta t = 2f_0 = 1\hspace{0.05cm} \rm kHz$ erhält man:

$$H_{\rm MF} ( {f = {1}/{\Delta t}} ) = {\rm{e}}^{ - {\rm{\pi }}} \cdot \left( {1 + 2^2 } \right) \hspace{0.15cm}\underline {= 0.216}.$$

(3)  Allgemein gilt für das S/N–Verhältnis am Ausgang des Matched-Filters:

$$\rho _d = \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{\it{\Phi _n} \left( f \right)}\,\,{\rm{d}}f = } \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{N_0 /2}} \, \,{\rm{d}}f \hspace{0.3cm}+ \hspace{0.3cm} \int_{ - \infty }^{ + \infty } {\frac{\left| {G(f)} \right|^2 }{N_0 /2}} \cdot \frac{f^2 }{f_0 ^2 }\,\,{\rm{d}}f.$$

Der erste Summand ist gleich dem S/N–Verhältnis bei weißem Rauschen. Für den zweiten Summanden erhält man:

$$\Delta \rho _d = \frac{g_0 ^2 \cdot \Delta t^2 }{N_0 /2 \cdot f_0 ^2 }\cdot \int_{ - \infty }^{ + \infty } {f^2 \cdot {\rm{e}}^{ - 2{\rm{\pi }}\left( {f \cdot \Delta t} \right)^2 } }\,\, {\rm{d}}f.$$

Nach der Substitution $x = 2 \cdot \pi^{0.5}\cdot f \cdot \Delta t$ lautet dieses Integral:

$$\Delta \rho _d = \frac{\sqrt 2 \cdot g_0 ^2 \cdot \Delta t}{N_0 } \cdot \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }} \cdot \int_{ - \infty }^{ + \infty } {\frac{x^2 }{\sqrt {2{\rm{\pi }}} }} \cdot {\rm{e}}^{ - x^2 /2}\,\, {\rm{d}}x.$$

Dieses bestimmte Integral wurde vorne angegeben; es hat den Wert $1$. Der erste Faktor beschreibt wiederum das S/N–Verhältnis bei weißem Rauschen. Damit ergeben sich folgende Gleichungen:

$$\Delta \rho _d = \rho _{d,\rm WR} \cdot \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }}, \hspace{1cm} \rho _d = \rho _{d,\rm WR} + \Delta \rho _d = \rho _{d, \rm WR} \left( {1 + \frac{1}{{4{\rm{\pi }}\left( {\Delta t \cdot f_0 } \right)^2 }}} \right).$$

$$\Rightarrow \hspace{0.3cm} \Delta t \cdot f_0 = 0.5 : \hspace{0.3cm} \rho _d = 1.318 \cdot \rho _{d,\rm WR} = 7.46 \cdot 10^3 \hspace{0.3cm} \Rightarrow \quad 10\lg \rho _d \hspace{0.15cm}\underline {= 38.73\;{\rm{dB}}}.$$

Es ergibt sich ein um $1.2 \; \rm dB$ besseres Ergebnis als bei weißem Rauschen, da hier ${\it \Phi}_n(f)$ im gesamten Frequenzbereich mit Ausnahme der Frequenz $f = 0$ (hier gilt das Gleichheitszeichen) kleiner ist als $N_0/2$. Diese Tatsache wird auch vom Matched–Filter ausgenutzt.