Aufgaben:Aufgabe 5.7Z: Nochmals McCullough-Modell

• Zurück zum Buch

Fehlerabstandsverteilung und -korrelationsfunktion von GE–Modell und äquivalentem MC-Modell

Wir betrachten wie auch in den Aufgaben A5.6, Z5.6 und A5.7 das Bündelfehler–Kanalmodell nach Gilbert und Elliott (GE–Modell) mit den Kenngrößen

$$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,$$

$$ p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$

Aus diesen vier Wahrscheinlichkeiten lassen sich die entsprechenden Kenngrößen des Kanalmodells nach McCullough (MC–Modell) so ermitteln, dass beide Modelle die genau gleichen statistischen Eigenschaften besitzen, nämlich

• exakt gleiche Fehlerabstandsverteilung $V_a(k)$,
• exakt gleiche Fehlerkorrelationsfunktion $\varphi_e(k)$.

Die Wahrscheinlichkeiten des MC–Modells wurden in der Aufgabe A5.7 wie folgt ermittelt (Bezeichnungen entsprechend der Grafik zur Aufgabe A5.7, alle mit „$q$” anstelle von „$p$”):

$$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.0061, \hspace{0.2cm}q_{\rm B} = 0.1949,$$

$$ q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5528, \hspace{0.2cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.3724\hspace{0.05cm}.$$

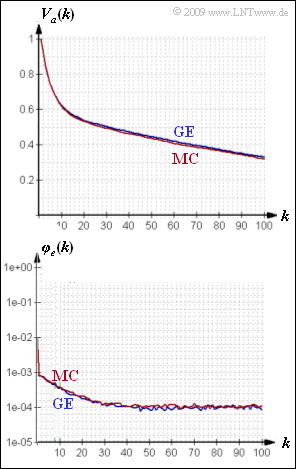
Die obere Grafik zeigt die aus $N = 10^6$ Folgenelementen simulativ ermittelten Funktionen $V_a(k)$ und $\varphi_e(k)$ für das GE– und das MC–Modell. Hier ergeben sich noch leichte Abweichungen. Im Grenzfall für $N → ∞$ stimmen dagegen Fehlerkorrelationsfunktion und Fehlerabstandsverteilung beider Modelle exakt überein.

In dieser Aufgabe sollen nun wichtige Beschreibungsgrößen wie Zustandswahrscheinlichkeiten, mittlere Fehlerwahrscheinlichkeiten und Korrelationsdauer direkt aus den $q$–Parametern des MC–Modells ermittelt werden.

Hinweise:

• Die Aufgabe gehört zum Themengebiet des Kapitels Bündelfehlerkanäle.
• Aus den oben genannten Aufgaben können folgende Ergebnisse weiterverwendet werden:

1. - Die Zustandswahrscheinlichkeiten des GE–Modells sind

$$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.05cm}.$$

1. - Die mittlere Fehlerwahrscheinlichkeit des GE–Modells beträgt

$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \varphi_{e}(k = 0 )\hspace{0.05cm}.$$

1. - Die Korrelationsdauer des GE–Modells berechnet sich zu

$$D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie die Wahrscheinlichkeiten $\alpha_G$ und $\alpha_B$, dass sich das MC–Modell im Zustand „G” bzw. im Zustand „B” befindet.

$\alpha_{\rm G} \ = \ $

$\alpha_{\rm B} \ = \ $

2

Ermitteln Sie den mittleren Fehlerabstand des MC–Modells.

${\rm E}[a] \ = \ $

3

Wie groß ist der FKF–Wert für $k = 0$?

$\varphi_e(k = 0) \ = \ $

4

Geben Sie die Fehlerkorrelationsdauer $D_{\rm K}$ als Funktion der MC–Parameter $q_{\rm G}, q_{\rm B}, q(\rm G|B)$ und $q(\rm B|G)$ an. Welches Ergebnis ist richtig?

	$D_{\rm K} = [q({\rm B|G}) + q({\rm G|B})]^{–1} \ –1$,
	$D_{\rm K} = [q_{\rm G} \cdot q({\rm G|B}) + q_{\rm B} \cdot q({\rm G|B})]^{–1} \ –1$.

Musterlösung

Musterlösung

(1)  Für die Zustandswahrscheinlichkeiten des GE–Modells wurde in Aufgabe Z5.6 ermittelt:

$$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = 0.909 \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }= 0.091\hspace{0.05cm}.$$

Dagegen erhält man beim MC–Modell:

$$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}= \frac{0.5528}{0.5528 + 0.3724}\hspace{0.15cm}\underline {= 0.5975}\hspace{0.05cm},$$

$$\alpha_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - \alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$

In der Teilaufgabe (3) der Aufgabe A5.7 wurden diese Werte schon einmal ermittelt, allerdings aus den Parametern des äquivalenten Gilbert–Elliott–Modells.

(2)  Der mittlere Fehlerabstand im Kanalzustand „FOOD” ist gleich dem Kehrwert der dazugehörigen Fehlerwahrscheinlichkeit $q_{\rm G}$. Der mittlere Fehlerabstand im Zustand „B” ist dementsprechend $1/q_{\rm B}$. Durch Gewichtung mit den beiden Zustandswahrscheinlichkeiten $\alpha_{\rm G}$ und $\alpha_{\rm B}$ ergibt sich der mittlere Fehlerabstand des MC–Modells insgesamt zu

$${\rm E}[a] =\frac{\alpha_{\rm G}}{q_{\rm G}} + \frac{\alpha_{\rm B}}{q_{\rm B}}=\frac{0.5975}{0.0061} + \frac{0.4025}{0.1949} = 97.95 + 2.06\hspace{0.15cm}\underline { = 100.1}\hspace{0.05cm}.$$

Dieser Wert sollte natürlich genau so groß wie beim entsprechenden GE–Modell sein. Die kleine Abweichung von $0.1$ ist auf Rundungsfehler zurückzuführen.

(3)  Auch hier gilt der Zusammenhang $\varphi_e(k = 0) = p_{\rm M}$. Die mittlere Fehlerwahrscheinlichkeit ist aber gleich dem Kehrwert des mittleren Fehlerabstands ${\rm E}[a]$. Daraus $\varphi_e(k = 0) \ \underline {= 0.01}$.

(4)  Beim GE–Modell ist die Korrelationsdauer wie folgt gegeben ($S$ steht für Summe):

$$D_{\rm K} = {1}/{S}-1 \hspace{0.05cm},\hspace{0.2cm}S = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$

Weiter gilt mit den Angaben zur Aufgabe A5.7:

$$q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) = \frac{\alpha_{\rm B} \cdot S}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, \hspace{0.2cm}q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })= \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$$

$$\Rightarrow \hspace{0.3cm} S = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) + q_{\rm B} \cdot \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B }) \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm}D_{\rm K} =\frac{1}{q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })}-1 \hspace{0.05cm}.$$

Richtig ist also der Lösungsvorschlag 2. Mit den gegebenen Parameterwerten erhält man zum Beispiel:

$$D_{\rm K} =\frac{1}{0.0061 \cdot 0.3724 + 0.1949 \cdot 0.5528}-1=\frac{1}{0.11}-1 {\approx 8.09}\hspace{0.05cm}.$$

Es ergibt sich exakt der gleiche Wert wie in der Aufgabe A5.6c.