Aufgaben:Aufgabe 5.6Z: Nochmals Filterdimensionierung: Unterschied zwischen den Versionen
K (Guenter verschob die Seite Aufgabe 5.6Z: Nochmals FIlterdimensionierung nach Aufgabe 5.6Z: Nochmals Filterdimensionierung) |
|||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
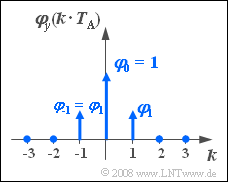
| − | [[Datei:P_ID567__Sto_Z_5_6.png|right| | + | [[Datei:P_ID567__Sto_Z_5_6.png|right|frame|Gewünschte AKF $\varphi_y(k \cdot T_{\rm A})$]] |
| − | Mit Hilfe eines nichtrekursiven digitalen Filters erster Ordnung soll eine zeitdiskrete Zufallsgröße $\left\langle {y_\nu } \right\rangle$ generiert werden, die folgende AKF-Werte aufweist: | + | Mit Hilfe eines nichtrekursiven digitalen Filters erster Ordnung soll eine zeitdiskrete Zufallsgröße $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ generiert werden, die folgende AKF-Werte aufweist: |
:$$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm f\ddot{u}r} & {k = 0} \\ {\varphi _1 } & {\rm f\ddot{u}r} & {\left| k \right| = 1} \\ 0 & {} & {{\rm{sonst}}.} \\ \end{array}} \right.$$ | :$$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm f\ddot{u}r} & {k = 0} \\ {\varphi _1 } & {\rm f\ddot{u}r} & {\left| k \right| = 1} \\ 0 & {} & {{\rm{sonst}}.} \\ \end{array}} \right.$$ | ||
| − | Hierbei bezeichnet $\varphi_1$ einen (in bestimmten Grenzen) frei wählbaren Parameter. | + | Hierbei bezeichnet $\varphi_1$ einen (in bestimmten Grenzen) frei wählbaren Parameter. |
| − | + | Weiter gelte: | |
| − | |||
| + | * Die zeitdiskreten Eingangswerte $x_\nu$ sind gaußverteilt mit Mittelwert $m_x$ und Streuung $\sigma_x$. | ||
| + | * Für die gesamte Aufgabe gilt $\sigma_x= 1$. Der Mittelert sei zunächst $m_x = 0$. | ||
| + | *In der Teilaufgabe '''(4)''' gelte $m_x = 1$. | ||
| − | Damit lautet das Gleichungssystem zur Bestimmung der Filterkoeffizienten $a_0$ und $a_1$: | + | |
| + | Damit lautet das Gleichungssystem zur Bestimmung der Filterkoeffizienten $a_0$ und $a_1$: | ||
:$$a_0 ^2 + a_1 ^2 = 1, \hspace{0.5cm} | :$$a_0 ^2 + a_1 ^2 = 1, \hspace{0.5cm} | ||
| − | a_0 \cdot a_1 = \ | + | a_0 \cdot a_1 = \varphi_1 .$$ |
| + | |||
| + | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Erzeugung_vorgegebener_AKF-Eigenschaften|Erzeugung vorgegebener AKF-Eigenschaften]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Erzeugung_vorgegebener_AKF-Eigenschaften|Erzeugung vorgegebener AKF-Eigenschaften]]. |
| − | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. | + | *Bezug genommen wird auch auf das Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. |
| Zeile 28: | Zeile 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lauten die | + | {Wie lauten die zulässigen Grenzwerte für $\varphi_1$, damit das Gleichungssystem lösbar ist? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_\text{1, max} \ = $ { 0.5 3% } | + | $\varphi_\text{1, max} \ = \ $ { 0.5 3% } |
| − | $\varphi_\text{1, min} \ = $ { -0.515--0.485 } | + | $\varphi_\text{1, min} \ = \ $ { -0.515--0.485 } |
| − | {Es gelte $\varphi_1= -0.3$. Bestimmen Sie die Filterparameter $a_0$ und $a_1$. Wählen Sie die Lösung mit positivem $a_0$ und $ | + | {Es gelte $\varphi_1= -0.3$. Bestimmen Sie die Filterparameter $a_0$ und $a_1$. Wählen Sie die Lösung mit positivem $a_0$ und $|a_1| < a_0$. |
|type="{}"} | |type="{}"} | ||
| − | $a_0 \ = $ { 0.949 3% } | + | $a_0 \ = \ $ { 0.949 3% } |
| − | $a_1 \ = ${ -0.326--0.306 } | + | $a_1 \ = \ ${ -0.326--0.306 } |
| − | {Wie ändert sich die AKF, wenn nun bei gleichen Filterkoeffizienten | + | {Wie ändert sich die AKF, wenn nun bei gleichen Filterkoeffizienten $\sigma_x = 2$ gilt? Wie groß ist insbesondere der AKF–Wert für $k = 1 $? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_y(T_{\rm A}) \ = $ { -1.236--1.164 } | + | $\varphi_y(T_{\rm A}) \ = \ $ { -1.236--1.164 } |
| − | {Wie ändert sich die AKF bei gleichen Filterkoeffizienten und $\sigma_x = 2$ mit einem Gleichanteil $m_x = 1$? Wie groß ist nun der AKF-Wert für $k = 1 $? | + | {Wie ändert sich die AKF bei gleichen Filterkoeffizienten und $\sigma_x = 2$ mit einem Gleichanteil $m_x = 1$? Wie groß ist nun der AKF-Wert für $k = 1 $? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_y(T_{\rm A}) \ = $ { -0.82--0.78 } | + | $\varphi_y(T_{\rm A}) \ = \ $ { -0.82--0.78 } |
| Zeile 55: | Zeile 60: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Nach einigen Umformungen kommt man zur Bestimmungsgleichung (mit $u = a_0^2$ | + | '''(1)''' Nach einigen Umformungen kommt man zur Bestimmungsgleichung $($mit $u = a_0^2)$: |
:$$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | :$$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
a_1 = \varphi_1 /a_0 ,$$ | a_1 = \varphi_1 /a_0 ,$$ | ||
| Zeile 64: | Zeile 69: | ||
u^2 - u + \varphi_1^2 = 0.$$ | u^2 - u + \varphi_1^2 = 0.$$ | ||
| − | Dies führt zu den beiden Lösungen: | + | *Dies führt zu den beiden Lösungen: |
:$$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$ | :$$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$ | ||
| − | Reelle Lösungen gibt es nur für $\varphi_1^2 \le 0.25$. Das bedeutet: | + | *Reelle Lösungen gibt es nur für $\varphi_1^2 \le 0.25$. Das bedeutet: |
| − | :$$\hspace{0.15cm}\underline {\ | + | :$$\hspace{0.15cm}\underline {\varphi_\text{1, max} = +0.5}, \quad \hspace{0.15cm}\underline {\varphi_\text{1, min} = - 0.5}.$$ |
| + | |||
| + | |||
| − | '''(2)''' Mit $\varphi_1=-0.3$ erhält man $u_1 = 0.9$ und $u_2 = 0.1$. Daraus ergeben sich folgende Parametersätze: | + | '''(2)''' Mit $\varphi_1=-0.3$ erhält man $u_1 = 0.9$ und $u_2 = 0.1$. Daraus ergeben sich folgende Parametersätze: |
:$$\text{Lösung 1:} \ \ a_0 = \;\;\,\sqrt {0.9} = \;\;\, 0.949,\quad a_1 = - \sqrt {0.1} = - 0.316;$$ | :$$\text{Lösung 1:} \ \ a_0 = \;\;\,\sqrt {0.9} = \;\;\, 0.949,\quad a_1 = - \sqrt {0.1} = - 0.316;$$ | ||
:$$\text{Lösung 2:} \ \ a_0 = - \sqrt {0.9} = - 0.949,\quad a_1 = \;\;\, \sqrt {0.1} = \;\;\, 0.316;$$ | :$$\text{Lösung 2:} \ \ a_0 = - \sqrt {0.9} = - 0.949,\quad a_1 = \;\;\, \sqrt {0.1} = \;\;\, 0.316;$$ | ||
| Zeile 76: | Zeile 83: | ||
:$$\text{Lösung 4:} \ \ a_0 = - \sqrt {0.1} = - 0.316,\quad a_1 = \;\;\, \sqrt {0.9} = \;\;\, 0.949.$$ | :$$\text{Lösung 4:} \ \ a_0 = - \sqrt {0.1} = - 0.316,\quad a_1 = \;\;\, \sqrt {0.9} = \;\;\, 0.949.$$ | ||
| − | Nur der erste Parametersatz erfüllt die angegebene Nebenbedingung: $a_0 \hspace{0.15cm}\underline {= 0.949} | + | *Nur der erste Parametersatz erfüllt die angegebene Nebenbedingung: |
| + | :$$a_0 \hspace{0.15cm}\underline {= 0.949} \ \text{ und } \ a_1 \hspace{0.15cm}\underline {= -0.316}.$$ | ||
| + | |||
| − | '''(3)''' Wird $\sigma_x$ verdoppelt, so erhöhen sich alle AKF-Werte um den Faktor $4$. Insbesondere gilt dann: | + | '''(3)''' Wird $\sigma_x$ verdoppelt, so erhöhen sich alle AKF-Werte um den Faktor $4$. Insbesondere gilt dann: |
:$$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$ | :$$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$ | ||
| − | |||
| − | |||
| − | Alle AKF-Werte werden deshalb gegenüber der Teilaufgabe (3) um $m_y^2 \approx 0.4$ vergrößert und man erhält nun: | + | |
| + | '''(4)''' Der Gleichanteil $m_x = 1$ am Eingang führt zu folgendem Gleichanteil im Ausgangssignal: | ||
| + | :$$m_y = m_x \cdot ( {a_0 + a_1 } ) = 1 \cdot (0.949 -0.316) = 0.633.$$ | ||
| + | |||
| + | *Alle AKF-Werte werden deshalb gegenüber der Teilaufgabe '''(3)''' um $m_y^2 \approx 0.4$ vergrößert und man erhält nun: | ||
:$$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$ | :$$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 21. Februar 2022, 12:39 Uhr
Mit Hilfe eines nichtrekursiven digitalen Filters erster Ordnung soll eine zeitdiskrete Zufallsgröße $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ generiert werden, die folgende AKF-Werte aufweist:
- $$\varphi _y ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\varphi _0 = 1} & {\rm f\ddot{u}r} & {k = 0} \\ {\varphi _1 } & {\rm f\ddot{u}r} & {\left| k \right| = 1} \\ 0 & {} & {{\rm{sonst}}.} \\ \end{array}} \right.$$
Hierbei bezeichnet $\varphi_1$ einen (in bestimmten Grenzen) frei wählbaren Parameter.
Weiter gelte:
- Die zeitdiskreten Eingangswerte $x_\nu$ sind gaußverteilt mit Mittelwert $m_x$ und Streuung $\sigma_x$.
- Für die gesamte Aufgabe gilt $\sigma_x= 1$. Der Mittelert sei zunächst $m_x = 0$.
- In der Teilaufgabe (4) gelte $m_x = 1$.
Damit lautet das Gleichungssystem zur Bestimmung der Filterkoeffizienten $a_0$ und $a_1$:
- $$a_0 ^2 + a_1 ^2 = 1, \hspace{0.5cm} a_0 \cdot a_1 = \varphi_1 .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Erzeugung vorgegebener AKF-Eigenschaften.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
Fragebogen
Musterlösung
- $$a_0 \cdot a_1 = \varphi_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} a_1 = \varphi_1 /a_0 ,$$
- $$a_0^2 + a_1^2 = 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} a_0^2 + \varphi_1^2 /a_0^2 -1 = 0,$$
- $$u = a_0^2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} u + \varphi_1^2 /u -1 = 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} u^2 - u + \varphi_1^2 = 0.$$
- Dies führt zu den beiden Lösungen:
- $$u_{1/2} = 0.5 \pm \sqrt {0.25 - \varphi _1 ^2 } .$$
- Reelle Lösungen gibt es nur für $\varphi_1^2 \le 0.25$. Das bedeutet:
- $$\hspace{0.15cm}\underline {\varphi_\text{1, max} = +0.5}, \quad \hspace{0.15cm}\underline {\varphi_\text{1, min} = - 0.5}.$$
(2) Mit $\varphi_1=-0.3$ erhält man $u_1 = 0.9$ und $u_2 = 0.1$. Daraus ergeben sich folgende Parametersätze:
- $$\text{Lösung 1:} \ \ a_0 = \;\;\,\sqrt {0.9} = \;\;\, 0.949,\quad a_1 = - \sqrt {0.1} = - 0.316;$$
- $$\text{Lösung 2:} \ \ a_0 = - \sqrt {0.9} = - 0.949,\quad a_1 = \;\;\, \sqrt {0.1} = \;\;\, 0.316;$$
- $$\text{Lösung 3:} \ \ a_0 = \;\;\, \sqrt {0.1} = \;\;\, 0.316,\quad a_1 = - \sqrt {0.9} = - 0.949;$$
- $$\text{Lösung 4:} \ \ a_0 = - \sqrt {0.1} = - 0.316,\quad a_1 = \;\;\, \sqrt {0.9} = \;\;\, 0.949.$$
- Nur der erste Parametersatz erfüllt die angegebene Nebenbedingung:
- $$a_0 \hspace{0.15cm}\underline {= 0.949} \ \text{ und } \ a_1 \hspace{0.15cm}\underline {= -0.316}.$$
(3) Wird $\sigma_x$ verdoppelt, so erhöhen sich alle AKF-Werte um den Faktor $4$. Insbesondere gilt dann:
- $$\varphi _y( {T_{\rm A} } ) = - 0.3 \cdot 4 \hspace{0.15cm}\underline{= - 1.2}.$$
(4) Der Gleichanteil $m_x = 1$ am Eingang führt zu folgendem Gleichanteil im Ausgangssignal:
- $$m_y = m_x \cdot ( {a_0 + a_1 } ) = 1 \cdot (0.949 -0.316) = 0.633.$$
- Alle AKF-Werte werden deshalb gegenüber der Teilaufgabe (3) um $m_y^2 \approx 0.4$ vergrößert und man erhält nun:
- $$\varphi _y( {T_{\rm A} } )\hspace{0.15cm}\underline{ \approx - 0.8}.$$