Aufgaben:Aufgabe 5.3Z: Nichtrekursives Filter

• Zurück zum Buch

Nichtrekursives Filter

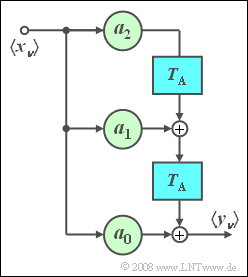
Betrachtet wird das nebenstehende nichtrekursive Filter mit den Filterkoeffizienten

$$a_0 = 1,\quad a_1 = 2,\quad a_2 = 1.$$

Gesucht sind die jeweiligen Ausgangsfolgen $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$, wenn am Eingang folgende Wertefolgen angelegt werden:

• die Gleichfolge

$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{g_\nu } \right\rangle = \left\langle {\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;1,\;\text{...} } \hspace{0.05cm} \right\rangle .$$

• die Sinusfolge  mit der Periodendauer $T_0 = 4 \cdot T_{\rm A}$:

$$\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{s_\nu } \right\rangle = \left\langle {\;0,\;1,\;0, - 1,\;0,\;1,\;0, - 1,\;\text{...} } \hspace{0.05cm}\right\rangle .$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Digitale Filter im vorliegenden Buch.
• Bezug genommen wird auch auf einige Kapitel im Buch Signaldarstellung.

Fragebogen

1

Wie lautet die Filter–Impulsantwort $h(t)$? Zu welchem Zeitpunkt $\nu \cdot T_{\rm A}$ hat diese ihr Maximum?

$\nu \ = \ $

2

Berechnen Sie den Frequenzgang $H(f)$. Wie groß ist der Wert bei $f = 0$?

$H(f = 0) \ = \ $

3

Welche Ausgangsfolge $\left\langle \hspace{0.05cm} {y_\nu } \hspace{0.05cm} \right\rangle$ ergibt sich für die Gleichfolge $\left\langle \hspace{0.05cm} {g_\nu } \hspace{0.05cm}\right\rangle$ an seinem Eingang? Interpretieren Sie dieses Ergebnis unter Berücksichtigung der letzten Teilaufgabe.
Welcher Ausgangswert ergibt sich für $\nu = 4 $?

$y_4 \ = \ $

4

Welche Ausgangsfolge $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$ ergibt sich für die Folge $\left\langle \hspace{0.05cm}{s_\nu } \hspace{0.05cm}\right\rangle$ am Eingang?
Welcher Ausgangswert ergibt sich für $\nu = 4 $?

$y_4 \ = \ $

Musterlösung

Musterlösung

(1)   Die Impulsantwort lautet:   $h(t) = \delta (t) + 2 \cdot \delta ( {t - T_{\rm A} } ) + \delta ( {t - 2T_{\rm A} } ).$ Das Maximum liegt bei $T_{\rm A}$,   ⇒   $\underline{\nu = 1}$.

(2)   Der Frequenzgang $H(f)$ ist die Fouriertransformierte der Impulsantwort $h(t)$.

• Die um $T_{\rm A}$ nach links verschobene Impulsantwort

$$h\hspace{0.05cm}'(t) = \delta ( {t + T_{\rm A} } ) + 2 \cdot \delta ( t ) + \delta ( {t - T_{\rm A} } )$$

ist symmetrisch um $t= 0$ und hat dementsprechend den rein reellen Frequenzgang

$$H\hspace{0.05cm}'(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ].$$

• Durch Anwendung des Verschiebungssatzes folgt weiter:

$$H(f) = 2\big [ {1 + \cos ( {2{\rm{\pi }}fT_{\rm A} } )} \big ] \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}fT_{\rm A} } .$$

• Der Wert des Frequenzgangs bei der Frequenz $f=0$ ist demzufolge $H(f = 0)\hspace{0.15cm}\underline{ = 4}$.

(3)   Die zeitdiskrete Faltung der Eingangsfolge $\left\langle \hspace{0.05cm}{g_\nu } \hspace{0.05cm} \right\rangle$ mit der Impulsantwort $\left\langle \hspace{0.05cm}{h_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{1, 2, 1 } \hspace{0.05cm}\right\rangle$ ergibt

$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle {\;1,\;3,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\;4,\; \text{...} \;} \right\rangle $$

• Insbesondere gilt $y_4\hspace{0.15cm}\underline{ = 4}$.
• Mit Ausnahme der Werte $y_0$ und $y_1$ (Einschwingvorgang) erhält man auch am Ausgang eine Gleichfolge mit dem konstanten Wert 4: :$$y(t) = H( {f = 0} ) \cdot x( t ) = 4 \cdot 1 = 4.$$

(4)   Analog zur Teilaufgabe (3) erhält man nun durch Verschiebung, Gewichtung mit $a_1$, $a_2$, $a_3$ und anschließender Überlagerung:

$$\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle = \left\langle \hspace{0.05cm}{\;0,\;1,\;2,\;0,\; - 2,\;0,\;2,\;0,\; - 2,\;0,\;...\;}\hspace{0.05cm} \right\rangle .$$

• Der gesuchte Wert ist somit $y_4\hspace{0.15cm}\underline{ = -2}$.

Anderer Lösungsweg:

• Die Eingangsfolge $\left\langle \hspace{0.05cm}{s_\nu }\hspace{0.05cm} \right\rangle$ verläuft sinusförmig mit der Periode $4 \cdot T_{\rm A}$. Die Grundfrequenz ist dementsprechend $f_0 = 1/(4 \cdot T_{\rm A})$.
• Bei dieser Frequenz hat der Frequenzgang $H(f)$ gemäß Teilaufgabe '(2) den folgenden Wert:

$$H( {f = f_0 } ) = 2\big[ {1 + \cos ( {{{\rm{\pi }}}/{2}} )} \big] \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} = 2 \cdot {\rm{e}}^{ - {\rm{j\pi /2}}} .$$

• Lässt man den Einschwingungsvorgang (abgeschlossen bei $t = T_{\rm A}$) außer Betracht, so ergibt sich mit $\tau = T_{\rm A}$   (Phase:   $90^\circ$)  folgender Zusammenhang zwischen dem Eingangs- und dem Ausgangssignal:

$$y(t) = 2 \cdot x( {t - T_{\rm A} } ).$$

• Das heißt:   Aus der Sinusfunktion wird die Funktion „Minus-Cosinus” mit der Amplitude 2.