Aufgabe 4.7: Kupfer-Doppelader 0.5 mm
Aus LNTwww
Version vom 1. Oktober 2016, 22:39 Uhr von Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Kupfer–Doppelader }} right| :Hier soll das Zeitverhalten einer Kup…“)
- Hier soll das Zeitverhalten einer Kupferdoppelader mit einem Durchmesser von 0.5 mm analysiert werden. Der Frequenzgang lautet mit der Leitungslänge l = 1.5 km und der Bitrate R = 10 Mbit/s:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm a}_0 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.01cm}\tau_{\rm P}} \cdot {\rm e}^{-{\rm a}_1 \hspace{0.05cm}\cdot \hspace{0.02cm}2f/R}\cdot \\ \cdot {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}} \hspace{0.05cm}.$$
- Hierbei sind folgende Größen verwendet, die sich aus dem Dämpfungs– und Phasenmaß ableiten lassen:
- $${\rm a}_0 = \alpha_0 \cdot l\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\alpha_0 = 0.5066\,\, \frac{\rm Np}{\rm km}\hspace{0.05cm},\\ \tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi} \hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\beta_1 = 30.6\,\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm},\\ {\rm a}_1 = \alpha_1 \cdot l \cdot {\frac{R}{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_1 = 0.136\,\, \frac{\rm Np}{\rm km \cdot MHz}\hspace{0.05cm},\\ {\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{\frac{R}{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_2 = 1.1467\,\, \frac{\rm Np}{\rm km \cdot MHz^{0.5}}\hspace{0.05cm},\\ {\rm b}_2 = \beta_2 \cdot l \cdot \sqrt{\frac{R}{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \beta_2 = 1.1467\,\, \frac{\rm rad}{\rm km \cdot MHz^{0.5}}\hspace{0.05cm}.$$
- Die Parameter α0, α1 und α2 wurden aus den k–Parametern umgerechnet, wie in der Aufgabe A4.6 gezeigt. Der Phasenmaßparameter β2 wurde hier zahlenmäßig gleich dem Dämpfungsmaßparameter α2 gesetzt. a2 und b2 unterscheiden sich deshalb nur in der Einheit. Im Theorieteil zu diesem Kapitel 4.3 wird dargelegt, warum diese Maßnahme erforderlich ist.
- Die Impulsantwort lässt sich somit in der Form
- $$h_{\rm K}(t ) = K \cdot \left [ \delta(t - \tau_{\rm P})\star h_{1}(t) \star h_{2}(t) \right ]$$
- darstellen, wobei
- die Teilimpulsantwort h1(t) auf den dritten Term in obiger Gleichung zurückgeht, und
- h2(t) die gemeinsame Zeitbereichsdarstellung der beiden letzten Terme angibt.
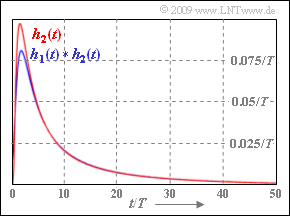
- Die Grafik zeigt den Anteil h2(t) der Impulsantwort und das Faltungsprodukt h1(t) ∗ h2(t). Dabei ist h2(t) gleich der Koaxialkabel–Impulsantwort mit der charakteristischen Kabeldämpfung a∗ = a2.
- Hinweis: Die Aufgabe beschreibt das Themengebiet von Kapitel 4.3.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.