Aufgaben:Aufgabe 4.7: Gewichtete Summe und Differenz

• Zurück zum Buch

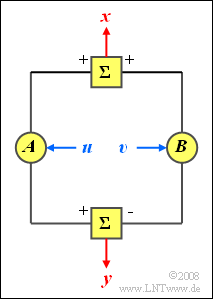
Die Zufallsgrößen $u$ und $v$ seien statistisch voneinander unabhängig, jeweils mit Mittelwert $m$ und Varianz $\sigma^2$. Beide Größen besitzen gleiche WDF und VTF. Über den Verlauf dieser Funktionen sei zunächst nichts bekannt.

Es werden nun zwei neue Zufallsgrößen $x$ und $y$ entsprechend den nachfolgenden Gleichungen gebildet:

$$x = A \cdot u + B \cdot v,$$

$$y= A \cdot u - B \cdot v.$$

Hierbei bezeichnen $A$ und $B$ (beliebige) konstante Werte.

• Für die Teilaufgaben (1) bis (4) gelte $m= 0$, $\sigma = 1$, $A = 1$ und $B = 2$.
• Bei der Teilaufgabe (5) wird vorausgesetzt, dass $u$ und $v$ jeweils gaußverteilt mit Mittelwert $m= 1$ und Streuung $\sigma = 0.5$ seien. Für die Konstanten gelte $A = B = 1$.
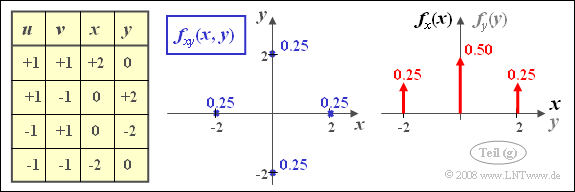
• Für die Aufgabe (6) gelte weiterhin $A = B = 1$. hier seien die Zufallsgrößen $u$ und $v$ symmetrisch zweipunktverteilt auf $\pm$1:

$${\rm Pr}(u=1) = {\rm Pr}(u=-1) = {\rm Pr}(v=1) = {\rm Pr}(v=-1) =0.5.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Wie groß sind Mittelwert und Streuung von $x$ für $A = 1$ und $B = 2$?

$m_x \ = $

$\sigma_x \ = $

2

Wie groß sind Mittelwert und Streuung von $y$ für $A = 1$ und $B = 2$?

$m_y \ = $

$\sigma_y \ = $

3

Berechnen Sie die Kovarianz $\mu_{xy}$. Welcher Wert ergibt sich für $A = 1$ und $B = 2$?

$\mu_{xy} \ = $

4

Berechnen Sie den Korrelationskoeffizienten $\rho_{xy}$ in Abhängigkeit des Quotienten $B/A$. Welcher Koeffizient ergibt sich für $A = 1$ und $B = 2$?

$\rho_{xy}\ = $

5

Welche der folgenden Aussagen gelten immer?

	Für $B = 0$ sind die Zufallsgrößen $x$ und $y$ streng korreliert.
	Es gilt $\rho_{xy}(-B/A) = -\rho_{xy}(B/A)$.
	Im Grenzfall $B/A \to \infty$ sind die Zufallsgrößen $x$ und $y$ streng korreliert.
	Für $A =B$ sind die Zufallsgrößen $x$ und $y$ unkorreliert.

6

Welche Aussagen sind zutreffend, wenn $A =B = 1$ gilt und $u$ und $v$ jeweils gaußverteilt sind mit Mittelwert $m = 1$ und Streuung $\sigma = 0.5$?

	Die Zufallsgrößen $x$ und $y$ sind unkorreliert.
	Die Zufallsgrößen $x$ und $y$ sind statistisch unabhängig.

7

Welche Aussagen treffen zu, wenn $u$ und $v$ symmetrisch zweipunktverteilt sind und $A =B = 1$ gilt?

	Die Zufallsgrößen $x$ und $y$ sind unkorreliert.
	Die Zufallsgrößen $x$ und $y$ sind statistisch unabhängig.

Musterlösung

Musterlösung

1. Da die Zufallsgrößen u und υ mittelwertfrei sind (m = 0), ist auch die Zufallsgröße x mittelwertfrei: m_x = (A + B) · m = 0. Für die Varianz und die Streuung gelten:

$$\sigma_x^2 = (A^2 +B^2) \cdot \sigma^2 = 5; \hspace{0.5cm} \sigma_x = \sqrt{5}\hspace{0.15cm}\underline{ \approx 2.236}.$$

2. Da u und υ die gleiche Streuung besitzen, gilt auch σ_y = σ_x ≈ 2.236. Wegen m = 0 gilt zudem m_y = 0. Bei mittelwertbehafteten Zufallsgrößen u und υ ergäbe sich für m_y = (A – B) · m dagegen ein anderer Wert als für m_x = (A + B) · m.

3. Wir gehen hier von dem allgemeineren Fall m ≠ 0 aus. Dann gilt für das gemeinsame Moment:

$$m_{xy} = {\rm E} [x \cdot y ] = {\rm E} [(A \cdot u + B \cdot v) (A \cdot u - B \cdot v)] . $$

Nach den allgemeinen Rechenregeln für Erwartungswerte folgt daraus:

$$m_{xy} = A^2 \cdot {\rm E} [u^2 ] - B^2 \cdot {\rm E} [v^2 ] = (A^2 - B^2)(m^2 + \sigma^2).$$

Die Kovarianz ergibt sich dann zu

$$\mu_{xy} = m_{xy} - m_{x} \cdot m_{y}= \\ = (A^2 - B^2)(m^2 + \sigma^2) - (A + B)(A-B) \cdot m^2 = (A^2 - B^2) \cdot \sigma^2.$$

Mit A = 1, B = 2, σ = 1 erhält man μ_xy = –3, unabhängig vom Mittelwert m der Größen u und υ.

4. Der Korrelationskoeffizient ergibt sich zu

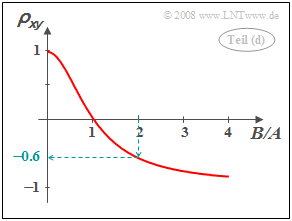
$$\rho_{xy} =\frac{\mu_{xy}}{\sigma_x \cdot \sigma_y} = \frac{(A^2 - B^2) \cdot \sigma^2}{(A^2 +B^2) \cdot \sigma^2} $$

$$\Rightarrow \rho_{xy} =\frac{1 - (B/A)^2} {1 +(B/A)^2}.$$

Mit B/A = 2 folgt daraus ρ_xy = –0.6.

5. Aus B = 0 folgt ρ_xy = 1 (strenge Korrelation). Aus den Gleichungen für x und y erkennt man weiter, dass in diesem Fall x und y identische Zufallsgrößen sind.

Die zweite Aussage ist nicht zutreffend: Für A = 1 und B = –2 ergibt sich ebenfalls ρ_xy = –0,6. Das Vorzeichen des Quotienten spielt also keine Rolle, weil in der unter (d) berechneten Gleichung B/A nur quadratisch auftritt.

Ist B sehr viel größer als A, so werden sowohl x als auch y fast ausschließlich durch die Zufallsgröße υ bestimmt und es ist y ≈ –x. Dies entspricht dem Korrelationskoeffizienten ρ_xy = –1. Dagegen ergibt sich für B/A = 1 stets der Korrelationskoeffizient ρ_xy = 0 und damit die Unkorreliertheit zwischen x und y.

Richtig sind somit die Aussagen 1, 3 und 4.

6. Bei A = B sind x und y stets (d. h. bei jeder beliebigen WDF der Größen u und υ) unkorreliert. Die neuen Zufallsgrößen x und y sind ebenfalls gaußverteilt. Bei Gaußschen Zufallsgrößen folgt aber aus der Unkorreliertheit auch die statistische Unabhängigkeit und umgekehrt. Also sind beide Aussagen richtig.

7. Der Korrelationskoeffizient ergibt sich mit A = B = 1 auch hier zu ρ_xy = 0. Das heißt, dass x und y unkorreliert sind. Dagegen erkennt man aus der nachfolgend skizzierten 2D-WDF, dass die Bedingung der statistischen Unabhängigkeit im nun vorliegenden Fall nicht mehr gegeben ist. Vielmehr gilt: f_xy(x, y) ≠ f_x(x) · f_y(y). Hier ist also nur die Aussage 1 zutreffend.